무거운 가격을 치르는 정규화 전문가 모델의 딜레마
📝 원문 정보
- Title: Geometric Regularization in Mixture-of-Experts The Disconnect Between Weights and Activations- ArXiv ID: 2601.00457
- 발행일: 2026-01-01
- 저자: Hyunjun Kim
📝 초록
이 논문은 Mixture-of-Experts(MoE) 모델에서 정교한 기능 다양성과 퍼플렉서티를 개선하기 위해 고안된 직교화 정규화의 실패를 분석한다. 다양한 데이터셋에 대한 실험 결과, 직교화 정규화는 예상대로 작동하지 않으며 가중치-활성화 간 연결이 약하다는 것을 확인했다.💡 논문 해설
1. **직교화 정규화의 실패**: 기존에는 직교화가 모델 성능을 개선할 것으로 생각되었지만, 실제로는 예상과 다르게 작동한다. 이는 마치 음식 조리에서 모든 재료를 같은 양으로 넣어도 맛이 좋지 않을 수 있는 것과 같다.-
가중치-활성화 간의 차이: 가중치의 직교성이 활성화 공간에서 유지되지 않는다는 것을 발견했다. 이는 건물 설계에서 구조를 설계하는 방식과 실제 건설 과정 사이에 큰 차이가 있을 수 있는 것과 비슷하다.
-
불안정한 결과: 다양한 데이터셋에서 직교화 정규화의 효과는 불안정하며, 이는 모델을 개선하기보다는 오히려 복잡성을 증가시킬 수 있다는 것을 시사한다.
📄 논문 발췌 (ArXiv Source)
Mixture-of-Experts (MoE) 모델은 입력당 매개변수의 일부만 활성화하여 효율적으로 확장됩니다. 일반적인 가정은 전문가 표현이 서로 직교되어야 한다는 것입니다. 이를 통해 중첩을 최소화할 수 있다고 생각합니다. 이 직관은 선형 대수학에서 나왔습니다: 직교 벡터는 가장 잘 구별되고 결합될 때 중첩되지 않습니다.
가설
직교화 정규화는 전문가 다양성을 향상시키고 perplexity를 줄여야 합니다.
발견
그렇지 않으며, 결과가 일관되지 않습니다. 세 가지 데이터셋(TinyStories, WikiText-103, PTB)에서 기하학적 정규화는 일관되지 않은 결과를 보입니다: WikiText-103에서 마진 개선($`-0.9\%`$), TinyStories에서는 약간의 저하($`+0.9\%`$), PTB에서 높은 변동성 (std $`>`$ 1.0).
왜?
우리는 가중치-활성화 간 차이를 발견했습니다: 가중치 공간 직교성(MSO $`\approx 10^{-4}`$)은 활성화 공간 직교성(MSO $`\approx 0.6`$)으로 전달되지 않습니다. 7개의 정규화 강도에서 가중치와 활성화 중첩 사이에 유의미한 상관관계가 없다는 것을 발견했습니다 ($`r = -0.293`$, $`p = 0.523`$), 이는 가중치 기하학과 함수적 직교성이 주로 독립적임을 나타냅니다.
기여
- 직교화 정규화는 실패하여 가중치 MSO를 줄이지 못하고 실제로 114%까지 증가시킵니다. 손실에도 일관되지 않은 효과를 미칩니다: WikiText-103에서 마진 개선($`-0.9\%`$), TinyStories에서는 약간의 저하($`+0.9\%`$), PTB에서 높은 변동성 (std $`>`$ 1.0).
- 가중치-활성화 간 단절: 활성화 중첩은 가중치 중첩보다 약 1000$`\times`$ 높으며, 유의미한 상관관계가 없습니다 ($`r = -0.293`$, $`p = 0.523`$, $`n`$=7).
- 가중치 공간 정규화는 불안정한 최적화 목표임을 보여줍니다—기하학적 목표를 달성하지 못하고 성능 개선도 일관되지 않습니다.
방법
직교 손실.
전문가 가중치 행렬 $`\{W_i\}_{i=1}^N`$에 대해 다음과 같이 정의합니다:
\begin{equation}
\mathcal{L}_{\text{orth}} = \sum_{i < j} |\langle \tilde{W}_i, \tilde{W}_j \rangle|^2
\label{eq:orth_loss}
\end{equation}여기서 $`\tilde{W}_i = \text{vec}(W_i) / \|\text{vec}(W_i)\|`$는 정규화된 평탄화 가중치 벡터입니다. 이 손실은 전문가 표현 사이의 직교성을 촉진하고 언어 모델링 목표에 가중치 $`\lambda`$와 함께 추가됩니다.
평균 제곱 중첩(MSO).
기하학적 다양성은 다음과 같이 측정합니다:
\begin{equation}
\text{MSO} = \frac{2}{N(N-1)} \sum_{i < j} |\langle \tilde{W}_i, \tilde{W}_j \rangle|^2
\end{equation}더 낮은 MSO는 더 직교(다양한) 전문가를 나타냅니다. 우리는 가중치와 활성화 모두에 대해 MSO를 계산합니다.
활성화 MSO.
공동 활성화된 전문가의 출력 $`\{h_i\}`$에 대해 다음과 같이 계산합니다:
\begin{equation}
\text{MSO}_{\text{act}} = \mathbb{E}_{x}\left[\frac{2}{k(k-1)} \sum_{i < j \in \mathcal{S}(x)} \left(\frac{\langle h_i, h_j \rangle}{\|h_i\|\|h_j\|}\right)^2\right]
\end{equation}여기서 $`\mathcal{S}(x)`$는 입력 $`x`$에 대한 선택된 전문가 집합입니다. 이는 실제 입력에서 전문가 출력 간의 기능적 유사성을 측정합니다.
실험
설정.
NanoGPT-MoE($`\sim`$ 130M 매개변수, 8 개의 전문가, 6 개의 계층, top-2 라우팅)을 10K 반복으로 TinyStories에서 학습합니다 (AdamW(lr=$`5 \times 10^{-4}`$, $`\beta_1`$=0.9, $`\beta_2`$=0.95, 가중치 감소=0.1). 각 MoE 계층은 숨겨진 차원이 512이고 중간 차원이 2048인 8 개의 전문가를 포함합니다. TinyStories 실험에서는 5개의 무작위 시드(42, 123, 456, 789, 1337)를 사용합니다.
구현 세부사항.
우리는 각 전문가의 업-프로젝션 가중치 ($`W_{\text{up}} \in \mathbb{R}^{d_{\text{ffn}} \times d_{\text{model}}}`$)를 정규화합니다. 각 가중치 행렬은 평탄화되고 L2-정규화된 후 쌍방향 내적을 계산합니다. $`\lambda`$ 스윕에는 7개의 값이 사용됩니다: $`\{0, 0.001, 0.005, 0.01, 0.05, 0.1, 0.2\}`$. MSO는 각 계층마다 계산되며 모든 6개 MoE 계층에 걸쳐 평균화됩니다. 활성화 MSO는 상위-2 선택된 전문가의 게이팅 스코어로 무게를 두지 않은 게이팅 후 전문가 출력에서 계산됩니다. 우리는 보조 부하 균형 손실을 사용하지 않습니다.
정규화 하에 가중치 MSO
표 1은 놀라운 발견을 드러냅니다: 직교화 정규화는 가중치 MSO를 줄이지 못하고 실제로 증가시킵니다. 손실이 명확하게 전문가 중첩을 벌금으로 부과하더라도, 최종 가중치 MSO는 $`\lambda`$ 증가에 따라 상승합니다. 이는 정규화가 자연 학습 동역학보다 직교성을 강제하는 대신 방해한다는 것을 시사합니다.
| Method | Weight MSO | $`\Delta`$ |
|---|---|---|
| Baseline | $`5.43 \times 10^{-4}`$ | — |
| + Orth ($`\lambda`$=0.001) | $`7.52 \times 10^{-4}`$ | $`+39\%`$ |
| + Orth ($`\lambda`$=0.01) | $`1.16 \times 10^{-3}`$ | $`+114\%`$ |
직교화 정규화는 가중치 MSO를 증가시키지만, 원래의 효과와는 반대입니다. 기준선 가중치는 이미 직교에 가깝습니다.
퍼플렉서티 개선이 없다
명시적인 정규화 목표에도 불구하고, 퍼플렉서티 개선은 통계적으로 유의미하지 않다 (표 2).
| Method | Val PPL | $`\Delta`$% | p-value |
|---|---|---|---|
| Baseline | $`5.94 \pm 0.08`$ | — | — |
| + Orth ($`\lambda`$=0.001) | $`6.00 \pm 0.32`$ | $`+0.9\%`$ | 0.727 |
직교화 정규화는 퍼플렉서티를 개선하지 않습니다 ($`p = 0.727`$, 쌍방향 t-검정, $`n`$=5 시드). 표준편차가 0.08에서 0.32로 증가합니다.
왜 p값이 높은가?
높은 p값($`p = 0.727`$)은 효과 크기의 최소성과 변동성 증가를 반영한다. 기준선은 낮은 표준편차(0.08)를 보이지만, $`\lambda`$=0.001은 변동성을 4$`\times`$ 증가시켜 학습을 불안정하게 만든다. PPL의 약간의 증가(+0.9%)는 이 변동성에 비해 작아 정규화가 혜택 없이 잡음을 추가한다는 것을 나타낸다.
가중치-활성화 간 차이
표 3은 핵심 발견을 드러냅니다: 가중치와 활성화 기하학은 근본적으로 분리되어 있습니다.
| $`\lambda`$ | Weight MSO | Act. MSO | Ratio |
|---|---|---|---|
| 0 (baseline) | $`5.43 \times 10^{-4}`$ | $`0.572`$ | 1053$`\times`$ |
| 0.001 | $`7.52 \times 10^{-4}`$ | $`0.581`$ | 773$`\times`$ |
| 0.01 | $`1.16 \times 10^{-3}`$ | $`0.577`$ | 496$`\times`$ |
| 0.1 | $`2.04 \times 10^{-3}`$ | $`0.593`$ | 290$`\times`$ |
| 0.2 | $`2.78 \times 10^{-3}`$ | $`0.564`$ | 203$`\times`$ |
활성화 MSO($`\sim`$ 0.57)은 일정하지만, 가중치 MSO는 $`\lambda`$ 증가에 따라 증가한다. Pearson $`r = -0.293`$, $`p = 0.523`$ ($`n`$=7), 이는 유의미한 상관관계를 나타내지 않는다.
상관 분석
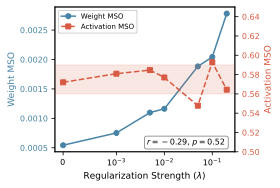
그림 1은 연결이 끊어진 것을 시각화한다: $`\lambda`$가 증가함에 따라 가중치 MSO는 증가하지만, 활성화 MSO는 약 0.57에서 일정하다. 7개의 정규화 강도에서 Pearson $`r = -0.293`$ ($`p = 0.523`$, 95% CI: $`[-0.857, 0.590]`$)—통계적으로 유의미하지 않다. 이는 가중치와 활성화 기하학이 독립적임을 확인한다.
 />
/>
데이터셋 간 검증
TinyStories를 넘어서 우리의 발견이 일반화되는지 확인하기 위해 WikiText-103과 Penn Treebank에서 직교화 정규화를 평가합니다—기하학적 특징이 다른 두 가지 표준 벤치마크 (표 4).
| Dataset | Tokens | Base | Orth | $`\Delta`$ |
|---|---|---|---|---|
| WikiText-103 | 118M | $`3.76_{\pm.02}`$ | $`3.73_{\pm.05}`$ | $`-0.9\%`$ |
| TinyStories | 2.1M | $`5.94_{\pm.08}`$ | $`6.00_{\pm.32}`$ | $`+0.9\%`$ |
| PTB | 1.2M | $`6.17_{\pm.95}`$ | $`5.74_{\pm1.11}`$ | $`-7.0\%^*`$ |
데이터셋 간 검증($`n`$=3 시드WikiText-103/PTB, $`n`$=5 TinyStories, $`\lambda`$=0.001). $`^*`$PTB에서 높은 변동성; 효과 방향이 불확실하다.
데이터셋 종속적 효과
다중 시드 실험은 혼합된 효과를 드러냅니다. WikiText-103 (118M 토큰)에서는 직교화 정규화가 작은 일관적인 개선을 보입니다 ($`-0.9\%`$). 그러나 PTB (1.2M 토큰)에서는 시드에 따라 결과가 매우 변동적으로 결론이 불확실합니다. 이 높은 변동성은 기하학적 정규화의 효과가 데이터셋-시드 상호작용에 의존할 수 있음을 시사한다.
해석
PTB에서의 높은 변동성(std $`\sim`$ 1.0)과 WikiText-103 (std $`\sim`$0.05)을 비교하면 데이터셋 규모 효과를 반영할 수 있습니다. 작은 데이터셋은 전문가 특수화 패턴에 더 많은 시드 의존성을 나타낼 수 있어 결과가 불안정해질 수 있습니다. 방향과 상관없이 불일관성 자체는 가중치 공간 정규화의 신뢰성을 해칩니다—특정 시드-데이터셋 조합에서만 작동하는 방법은 실용적이지 않습니다.
분석: 왜 차이가 존재할까?
비선형성의 역할
현대 MoE 전문가는 SiLU/Swish와 LayerNorm과 같은 비선형 활성화 함수를 사용합니다. 전문가 계산을 고려해보자:
\begin{equation}
h_i = \text{LayerNorm}(\text{SiLU}(W_i \cdot x))
\end{equation}$`W_i \perp W_j`$이라 하더라도 비선형성은 기하학을 복잡하게 변환합니다. SiLU는 활성화 크기에 따라 원소별 게이팅을 적용하고, LayerNorm은 활성화를 단위 분산으로 재중심화 및 재스케일링합니다. 이러한 연산은 전문가 출력 간의 각도 차이를 압축해 활성화 중첩을 증가시킬 수 있습니다.
입력 분포 효과
가중치 직교성은 정적 매개변수를 제약하지만, 활성화 직교성은 입력 분포에 의존합니다. 만약 입력 $`x`$가 서로 다른 가중치 하위공간으로 비슷하게 투영된다면 (예: 입력 분포의 저랭크 구조 때문), 결과적인 활성화 $`W_i \cdot x`$와 $`W_j \cdot x`$는 $`W_i \perp W_j`$일지라도 상관관계가 있을 수 있습니다. 자연어 입력은 이러한 구조를 가질 수 있습니다.
수학적 직관
두 개의 가중치 행렬 $`W_1, W_2`$와 Frobenius 직교성 $`\langle W_1, W_2 \rangle_F = \text{tr}(W_1^T W_2) = 0`$을 고려해보자. 이 제약은 $`W_1^T W_2`$의 합이 0이라는 것을 보장할 뿐 $`W_1^T W_2 = 0`$는 아닙니다. 입력 $`x`$에 대해 활성화 내적은 $`\langle z_1, z_2 \rangle = x^T W_1^T W_2 x`$. $`W_1^T W_2`$의 추이적 성분만 제약된다는 것을 고려하면 일반적인 입력에 대해 이 2차 형식은 일반적으로 0이 아닙니다. 따라서 가중치의 Frobenius 직교성은 활성화 직교성을 보장하지 않습니다.
관련 연구
MoE 확장 및 아키텍처
현대 MoE 패러다임은 천억 매개변수 스케일링을 통해 희소 게이팅으로 구현함으로써 시작되었습니다. Switch Transformers에서는 top-1 라우팅을 사용하여 이를 간소화했으며, GShard는 효율적인 분산 학습을 가능하게 했습니다. 최근 연구는 더 세밀한 전문가 분해를 탐구하고 있습니다: DeepSeekMoE는 계층당 64개의 세밀한 전문가를 사용하며, Mixtral은 top-2 라우팅을 사용하여 강력한 성능을 달성합니다. 이러한 아키텍처는 전문가 다양성이 학습 과정에서 자연스럽게 발생한다고 가정합니다.
전문가 특수화 및 다양성
여러 방법이 라우팅 개선을 통해 전문가 다양성을 해결하고 있습니다. X-MoE는 표현 붕괴를 완화하기 위해 하이퍼구 게이팅과 코사인 정규화된 게이팅을 사용합니다. HyperRouter은 하이페르네트워크를 통해 라우터 매개변수를 동적으로 생성합니다. S2MoE는 가우시안 노이즈를 사용한 확률적 학습으로 중첩된 전문가 특성을 방지합니다. ReMoE는 L1 정규화와 함께 ReLU 라우팅을 제안하여 차별 가능한 전문가 선택을 가능하게 합니다. SMoE-Dropout은 무작위 라우팅을 적용하여 전문가 붕괴를 방지합니다. CompeteSMoE는 표현 붕괴 문제를 해결하기 위해 경쟁 기반 라우팅을 사용합니다. 최근 분석에 따르면 계층 깊이가 증가함에 따라 전문가 다양성이 증가하지만, “전문가 특수화의 정도가 의심스럽다"는 결론을 내렸습니다. 제안된 직교 최적화자는 이러한 문제를 해결하려고 합니다. 우리의 결과는 이 회의감을 확장합니다: 가중치 공간 메트릭이 다양성을 나타내더라도 활성화 공간 중첩은 지속됩니다. 비록 라우팅 또는 최적화 다양성에 주력하지만, 우리는 직접 가중치 공간 기하학 제약을 분석합니다.
딥러닝에서의 기하학적 분석
Neural Collapse는 분류자 표현이 터미널 학습 중에 등각 긴 프레임(Equally Angular Tight Frames; ETFs)으로 수렴한다는 것을 보여줍니다. 이 기하학적 구조—클래스 표현이 최대한 분리됨—은 전문가 표현도 비슷하게 직교성을 통해 혜택을 받을 것이라는 우리의 가설을 영감을 줬습니다. 그러나 분류 헤드는 특징에서 로짓으로의 선형 맵핑입니다. 반면, MoE 전문가는 내부 구조를 갖춘 비선형 변환입니다. 우리의 부정적인 결과는 Neural Collapse 유사성이 깨진다는 것을 시사합니다: 비선형성은 기하학을 해칩니다.
논의
우리의 결과는 가중치 공간 직교성이 함수적 다양성을 이끌 것이라는 암묵적 가정에 도전한다. 단지 효과가 없는 것이 아니라, 기하학적 정규화는 불안정하다—TinyStories ($`-0.9\%`$)에서 마진 개선을 보이나 TinyStories ($`+0.9\%`$)에서는 저하되고 PTB에서 높은 변동성을 나타낸다.
MoE 설계에 대한 함의
- 가중치 공간 정규화는 불안정하다. 그 효과는 일관되지 않으며 일반적인 전략으로 적합하지 않습니다.
- 활성화 공간 정규화가 더 적절할 수 있다. 훈련 중 $`\text{MSO}_{\text{act}}`$를 직접 제약하여 기능적 다양성을 강제하면서 가중치-활성화 간의 연결을 극복할 수 있습니다.
- 자연 학습은 이미 낮은 가중치 MSO를 달성한다. 기준선 가중치 MSO($`\sim 10^{-4}`$)는 이미 직교에 가깝습니다.
📊 논문 시각자료 (Figures)
