보편 조건 논리 프롬프트 엔지니어링을 위한 형식 언어
📝 원문 정보
- Title: Universal Conditional Logic A Formal Language for Prompt Engineering- ArXiv ID: 2601.00880
- 발행일: 2025-12-31
- 저자: Anthony Mikinka
📝 초록
이 논문은 자연어 지시를 코드로 실행하는 대형 언어 모델(LLM)에 대한 새로운 패러다임을 제안한다. 이를 위해 *일반 조건 로직* (UCL)이라는 형식 언어를 도입하여, 프롬프트 엔지니어링을 체계적인 최적화로 이끈다. 또한, 지시의 상세 수준이 품질에 비선형적으로 영향을 미치는 '과도한 지시 패러독스'를 설명하고, 이를 극복하기 위한 구조적 오버헤드와 품질 함수를 제시한다.💡 논문 해설
1. **키 컨트리뷰션 1: UCL이라는 형식 언어** 자연어 지시를 코드로 변환하는 데 필요한 문법, 구문, 의미론을 제공하며 체계적인 최적화를 가능하게 한다. 이를 통해 프롬프트 엔지니어링이 직관에서 과학으로 진화한다.-
키 컨트리뷰션 2: 품질 함수와 구조적 오버헤드
지시의 상세 수준이 증가함에 따라 품질이 비선형적으로 변화한다는 것을 발견하고 이를 수학적으로 설명하며, 이로 인해 발생하는 세 가지 벌점 메커니즘을 제시한다. -
키 컨트리뷰션 3: 실험적 검증
다양한 모델과 데이터셋을 사용하여 UCL의 효과를 검증하고 이를 통해 프롬프트 엔지니어링에 대한 새로운 이해를 제공한다.
[Easy Level]
이 논문은 자연 언어 지시를 코드로 변환하는 방법을 개선하기 위해 새로운 패러다임인 UCL을 제안합니다. 이는 복잡한 프로그래밍 작업을 쉽게 만들 수 있도록 도와줍니다.
[Moderate Level]
UCL이라는 새로운 형식 언어를 통해 자연언어 지시를 코드로 변환하는 효율적인 방법을 소개합니다. 이를 통해 프롬프트 엔지니어링이 직관에서 과학으로 발전하고, 품질과 성능에 대한 깊은 이해를 제공합니다.
[Advanced Level]
이 논문은 자연언어 지시의 코드 변환을 체계적으로 최적화하기 위한 UCL이라는 형식 언어를 제안하며, 이를 통해 프롬프트 엔지니어링의 품질과 성능에 대한 깊은 이해와 검증을 제공합니다.
📄 논문 발췌 (ArXiv Source)
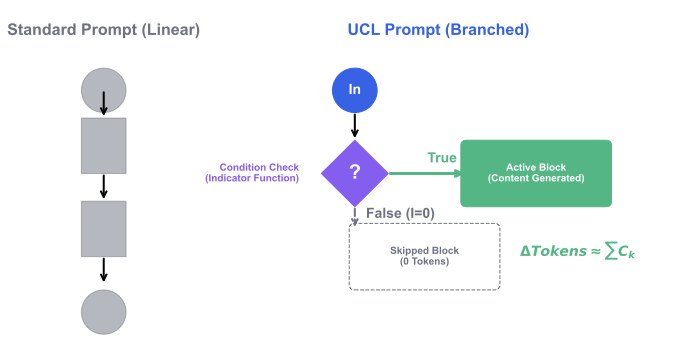
프롬프트 프로그래밍 패러다임
컴퓨팅 역사에서는 더 높은 추상화로의 진화가 보여진다: 기계어에서 어셈블리, 어셈블리에서 C, 명령형에서 선언형 패러다임. 대형 언어 모델(LLM)은 이 다음 전망지—자연어 지시를 코드로 실행하는 시스템을 나타낸다. 그러나 프롬프트 엔지니어링은 여전히 직관적이며, 정식 문법이나 체계적인 최적화가 부족하다.
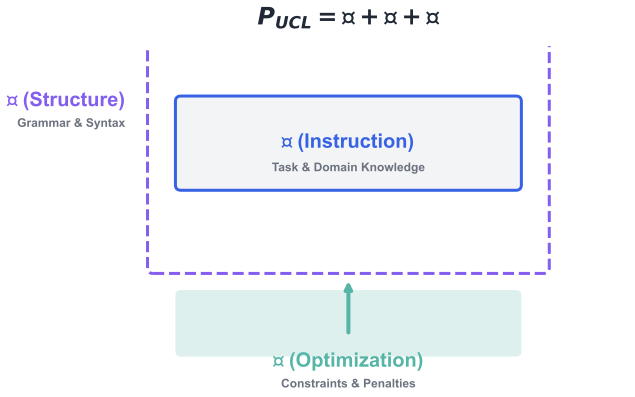
이 논문에서는 자연어를 최적화된 실행 구조로 변환하기 위한 형식 언어인 일반 조건 로직 (UCL)을 소개한다. C언어가 인간의 문법(if, while)을 효율적인 명령으로 컴파일하듯이, UCL은 다음과 같은 DSL을 제공한다:
-
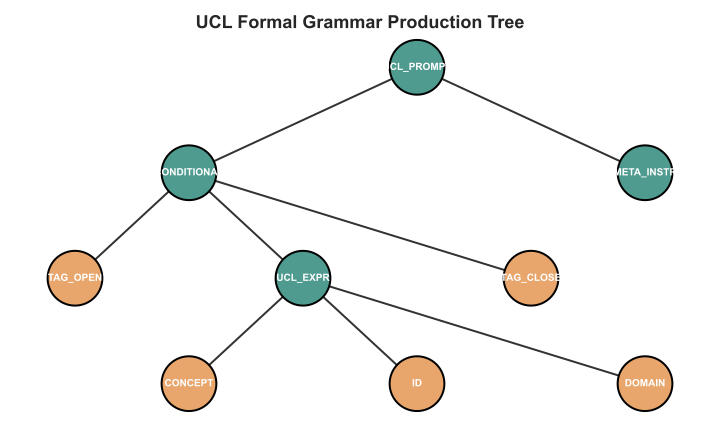
문법: 정상적인 프롬프트를 위한 생성 규칙
-
구문: 연산자 (
^^CONDITION:^^,[[LLM:]], {{concept:domain:spec}}) -
의미론: 구문을 동작에 매핑하는 지표 함수
-
용법: 효율적인 구성 원칙
이것은 체계적 최적화를 가능하게 하여 프롬프트 엔지니어링을 기술에서 과학으로 이끈다.
과도한 지시 패러독스
통상적인 견해는 상세 수준이 증가함에 따라 품질이 단조롭게 개선된다고 가정한다. 그러나 우리의 연구에서는 역설적인 현상을 발견했다:
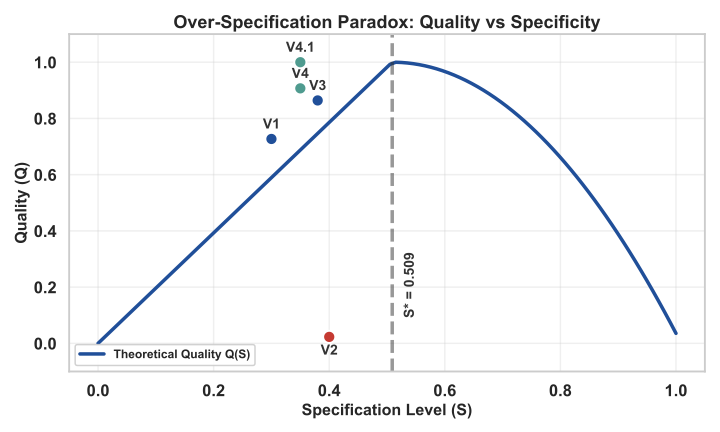
프롬프트의 품질은 지시의 상세 수준에 대해 비단조적이다.
$`S^*\approx 0.509`$을 초과하면, 추가적인 세부 사항이 세 가지 벌점으로 인해 품질을 저하시킨다:
\begin{equation}
Q(S) = \begin{cases}
\frac{Q_{\max}}{S^*} S & \text{if } S \leq S^*\\[0.5em]
Q_{\max}- b(S - S^*)^2 & \text{if } S > S^*
\end{cases}
\end{equation}여기서 $`Q_{\max}= 1.0`$, $`b = 4.0`$. 이것은 소프트웨어 개발에서의 과도한 공정과 유사하다: 과도한 주석은 유지보수 부담을 증가시킨다. 프롬프트에서는, 과도한 지시는 인지 유출—모델이 해결책 대신 내비게이션 논리를 출력하는 현상—을 일으킨다.
 style="width:90.0%" />
style="width:90.0%" />
세 가지 벌점 메커니즘:
-
역할 혼동 ($`P_{\text{role}} = \alpha_1 S^2`$): 이차적. 증거: V2에서 $`S=0.40`$일 때 $`Q = 0.02`$ (98% 실패)를 달성했다.
-
인지 복잡도 ($`P_{\text{complexity}} = \alpha_2 O_s`$): 선형적. 증거: V3에서 $`O_s= 28.85`$는 토큰이 4배로 늘어났다.
-
인식된 복잡도 ($`P_{\text{perceived}} = \alpha_3 \log|P|`$): 로그형. 증거: V4 (142줄)에서는 형식 실패가 발생했다.
구조적 오버헤드 검증
구조적 오버헤드 함수 $`O_s(\mathcal{A})`$는 각 버전에 대해 다음과 같이 계산된다:
\begin{equation}
O_s(\mathcal{A}) = \gamma \sum_{k \in \mathcal{K}} \ln(C_k) + \delta |L_{\text{proc}}|
\end{equation}여기서 $`\gamma = 1.0`$이고, $`\delta = 0.1`$이다.
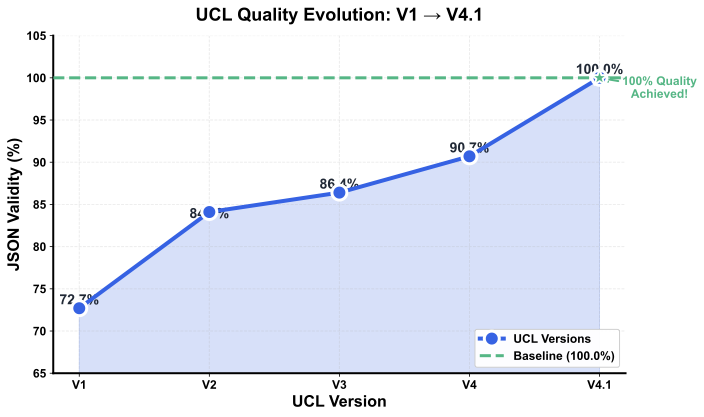
| 버전 | 아키텍처 | $`K`$ | $`\gamma\sum\ln(C_k)`$ | $`\delta|L|`$ | $`O_s`$ | 품질 | |:—|:–:|:–:|:–:|:–:|:–:|:–:| | V1 | 2 SWITCH (8+4) | 2 | 3.47 | 5.0 | 8.47 | 72.7% | | V2 | Nested SWITCH + COND | 2 | 3.47 | 15.0 | 35.47 | 84.1% | | V3 | 2 SWITCH + UNCONDITI | 2 | 3.47 | 10.0 | 13.47 | 86.4% | | V4 | 7 KEYWORD CONDITIONS | 0 | 0.00 | 2.0 | 2.00 | 90.7% | | V4.1 | Keywords + [[CRITICA | 0 | 0.00 | 2.0 | 2.00 | 100.0% |
구조적 오버헤드 구성 요소와 품질
주요 관찰 사항:
-
V1–V3는 SWITCH 아키텍처를 사용하여 입력에 상관없이 모든 경우가 해석된다.
-
V4–V4.1은 KEYWORD CONDITIONS를 사용하여 일치하는 블록만 활성화된다.
-
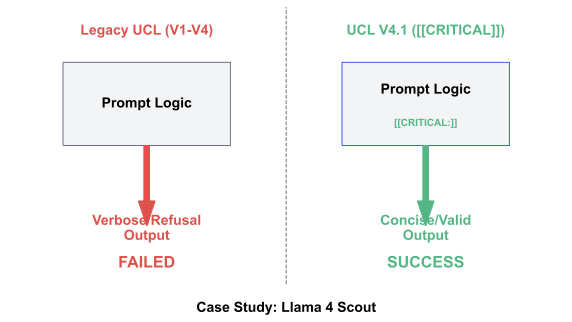
V4.1의
[[CRITICAL:]]지시문은 $`P_{\text{perceived}}`$을 차단하여 100% 품질을 달성한다.
 style="width:85.0%" />
style="width:85.0%" />
품질의 비선형성 시각화는 Figure 1 참조.
지표 함수 메커니즘
핵심 혁신: $`I_i(x) \in \{0,1\}`$은 관성 평가에 대한 선택적 활성화를 가능하게 한다:
정의 1 (지표 함수). *도메인 $`i`$와 키워드 $`K_i`$에 대해:
\begin{equation}
I_i(x) = \mathbb{1}[K_i \cap \text{tokens}(x) \neq \emptyset]
\end{equation}
```*
</div>
**아키텍처 비교:**
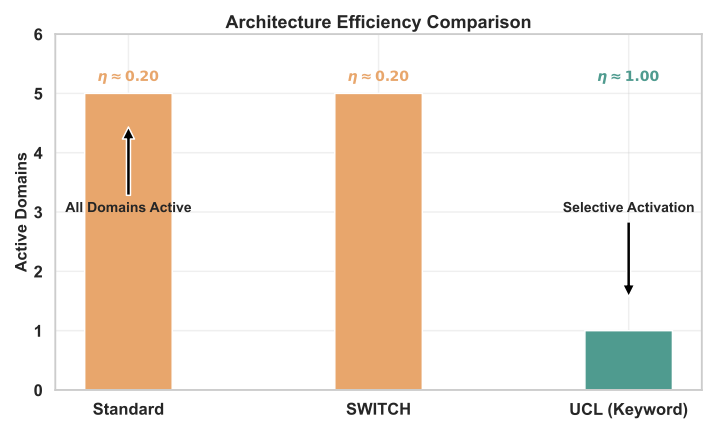
- 표준: 모든 활성화 ($`I_i = 1 ~\forall i`$), 효율 $`\eta = 1/D`$
- SWITCH: 모든 해석이 필요 ($`I_i \approx 1`$), 효율 $`\eta \approx 1/D`$
- UCL: 진정한 선택적 활성화 ($`I_i \in \{0,1\}`$), 효율 $`\eta \approx 1.0`$
프로그래밍 병렬:
- 사망 코드 제거 $`\equiv`$ $`O_s`$ 감소
- 관성 평가 $`\equiv`$ 지표 기반 활성화
- `#ifdef` $`\equiv`$ `CONDITION`
<figure id="fig:indicator_comparison" data-latex-placement="htbp">
<img src="/posts/2025/12/2025-12-31-190688-universal_conditional_logic__a_formal_language_for/figure2_indicator_comparison.png" style="width:100%" />
style="width:90.0%" />
<figcaption>프롬프트 아키텍처 간 지표 함수 비교. 각 셀은 "라인 적분"에 대한 입력으로 주어진 도메인의 활성화 상태 (<span
class="math inline"><em>I</em><sub><em>i</em></sub> ∈ {0, 1}</span>)를 보여줍니다. 표준 및 SWITCH 아키텍처는 모든 도메인이 활성화되며 (<span
class="math inline"><em>η</em> = 1.00</span>) 불필요한 내용을 처리합니다. UCL의 키워드 아키텍처는 관련 도메인만 활성화하여 (<span class="math inline"><em>η</em> = 0.40</span>) 선택적 실행과 토큰 절약을 달성합니다.</figcaption>
</figure>
## 기여
다섯 가지 주요 기여:
1. **형식 언어**: 문법, 검증된 구문, 의미론, 용법 (§4)
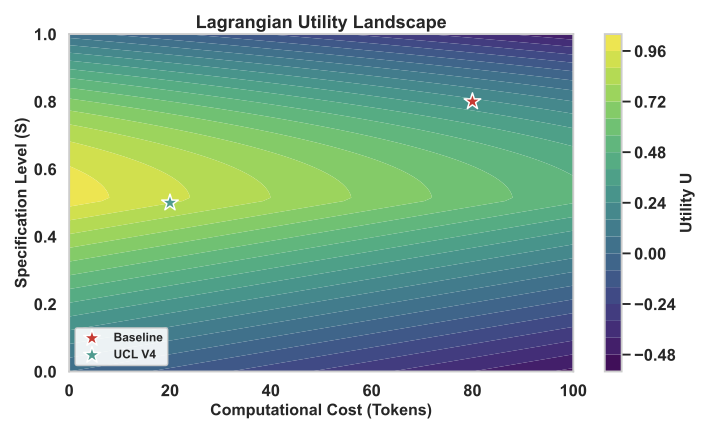
2. **수학적 근거**: 라그랑주 최적화, 품질 함수, 구조적 오버헤드 (§3)
3. **핵심 검증**: 11개 모델, N=305, $`p < 10^{-13}`$ (§5)
4. **확장 지시문**: 30+ 연산자와 검증 로드맵 (§6.2, 부록 B)
5. **프로그래밍 패러다임**: "프롬프트 컴파일" 프레임워크 (전반적으로)
K&R의 C나 Python PEPs처럼 핵심을 검증하며 확장성 테스트를 위한 커뮤니티 초대.
# 관련 연구
## 프롬프트 엔지니어링 접근법
초기 작업: few-shot learning, chain-of-thought, tree-of-thoughts. 최근에는 gradient-based optimization, evolutionary algorithms 등이 있다. 이러한 접근들은 *콘텐츠*를 최적화하며, *아키텍처*는 최적화하지 않는다.
**신생 패러다임:** 프롬프트 패턴은 재사용을 가능하게 한다. 문법 프롬프팅은 출력을 제한한다. DSPy는 구성 가능한 기본 단위를 제공한다.
**UCL의 위치:** 첫 번째 완전한 언어적 프레임워크. 조건부 효율성 $`\eta`$는 Haskell의 관성 평가와 유사하며, 구조적 오버헤드 $`O_s`$는 컴파일 시간 비용과 유사하다; 지표 함수는 if-guards를 실현한다.
## 컴파일러 및 프로그래밍 병렬
**컴파일러 최적화:** $`O_s`$ 감소는 사망 코드 제거, 루프 언롤링에 해당한다. 품질-비용 교환은 GCC의 `-O2` vs. `-O3`과 유사하다.
**정규화:** 과도한 지시는 과적합과 유사하다. L2 벌점이 용량을 제약하듯이, 우리의 벌점은 지시를 제약한다.
**정보 이론 (최소):** 과도한 지시는 "잡음"을 추가하여 $`C_{\text{eff}} = C_{\max} - O_s`$를 감소시킨다.
**DSLs:** UCL은 DSL 원칙을 따르며: 도메인 타겟팅, 적절한 추상화, 컴파일 가능하다.
기술이나 직관이 아닌 완전한 형식 언어와 검증된 메커니즘을 제공한다.
# 수학적 프레임워크
## 일반 프롬프트 방정식
<div id="def:universal-prompt" class="definition">
**정의 2** (일반 프롬프트 방정식).
*``` math
\begin{equation}
P(x) = V \circ R \circ B\left(T(x) + \sum_{i=1}^{n} I_i(x) \cdot D_i(x) + O_s(A)\right)
\end{equation}
```*
</div>
여기서 $`T`$=태스크, $`I_i`$=지표 함수, $`D_i`$=도메인, $`n`$=도메인 수, $`O_s`$=오버헤드, $`B`$=바인딩, $`R`$=역할, $`V`$=검증이며, $`A(x) = \{i : I_i(x) = 1\}`$는 활성 도메인 집합이다.
프로그래밍에 비유하면: $`I_i`$은 if-guards와 유사하며, $`O_s`$는 컴파일 비용과 같다.
<div id="rem:standard-vs-ucl" class="remark">
*비고 1* (표준 vs. UCL 프롬프트 차이). 일반 프롬프트 방정식은 표준 및 UCL 프롬프트 모두에 적용된다. 주요 차이는 지표 함수의 동작이다:
**표준 프롬프트:** 모든 $`i \in \{1, \ldots, n\}`$에 대해 $`I_i(x) = 1`$.
``` math
\begin{equation}
\label{eq:standard-prompt}
P_{\text{standard}}(x) = V \circ R \circ B\left(T(x) + \sum_{i=1}^{n} I_i(x) \cdot D_i(x) + O_s(A)\right)
\end{equation}모든 $`n`$ 도메인이 입력 $`x`$에 관계없이 포함된다. 지표 항은 $`I_i = 1`$이므로 사라진다.
UCL 프롬프트: $`I_i(x) = \mathbb{1}[K_i \cap \text{tokens}(x) \neq \emptyset]`$.
\begin{equation}
\label{eq:ucl-prompt}
P_{\text{UCL}}(x) = V \circ R \circ B\left(T(x) + \sum_{i \in A(x)} I_i(x) \cdot D_i(x) + O_s(A)\right)
\end{equation}여기서 $`A(x) = \{i : I_i(x) = 1\}`$는 활성 도메인 집합이다. 단지 $`|A(x)|`$ 도메인이 포함되며, 보통 $`|A(x)| \ll n`$이다.
콘텐츠 감소 정리: 입력 $`x`$가 정확히 하나의 도메인과 일치할 때 ($`|A(x)| = 1`$):
\begin{equation}
\label{eq:content-reduction}
\frac{\text{표준 콘텐츠}}{\text{UCL 콘텐츠}} = \frac{\sum_{i=1}^{n} |D_i|}{\sum_{i \in A(x)} |D_i|} \approx n
\end{equation}이 $`n`$-배 감소는 UCL의 효율성 향상의 주요 메커니즘이다.
 style="width:85.0%" />
style="width:85.0%" />
품질 함수
Figure 2에서 볼 수 있듯이, 구조적 오버헤드는 아키텍처에 따라 크게 달라진다.
정의 3. ``` math \begin{equation} Q(S) = \begin{cases} \frac{Q_{\max}}{S^} S & S \leq S^\[0.5em] Q_{\max}- b(S - S^)^2 & S > S^* \end{cases} \end{equation}
</div>
<div class="proof">
*증명.* $`S^*`$에서 연속성을 위해 좌우 극한은 같아야 한다:
``` math
\begin{align}
\lim_{S \to S^{*-}} Q(S) &= \lim_{S \to S^{*+}} Q(S) \\
\frac{Q_{\text{max}}}{S^*} \cdot S^* &= Q_{\text{max}} - b(S^* - S^*)^2 \\
Q_{\text{max}} &= Q_{\text{max}}
\intertext{기울기 연속성을 위해 미분 값이 일치해야 한다:}
\left. \frac{d}{dS}\left[\frac{Q_{\text{max}}}{S^*}S\right] \right|_{S=S^*} &= \left. \frac{d}{dS}[Q_{\text{max}} - b(S-S^*)^2] \right|_{S=S^*} \\
\frac{Q_{\text{max}}}{S^*} &= 0
\end{align}이것은 $`a = Q_{\text{max}}/S^*`$를 강제하며, $`a = 1.0/0.509 \approx 1.96`$. ◻
 style="width:90.0%" />
style="width:90.0%" />
벌점 메커니즘 유도
역할 혼동 벌점:
\begin{equation}
P_{\text{role}}(S) = \alpha_1(S - S^*)^2 \quad \text{for } S > S^*
\end{equation}이차형태는 충돌 지시문으로 인한 지수적 저하를 포착한다. V2 실패에서 $`\alpha_1 = 2.5`$로 추정된다.
인지 복잡도 벌점:
\begin{equation}
P_{\text{complexity}} = \alpha_2 \cdot O_s = \alpha_2(\gamma\sum\ln C_k + \delta|L_{\text{proc}}|)
\end{equation}선형 오버헤드는 주의 능력 제한을 반영한다. V3 토큰 팽창에서 $`\alpha_2 = 0.08`$로 추정된다.
인식된 복잡도 벌점:
\begin{equation}
P_{\text{perceived}} = \alpha_3 \ln(|P|)
\end{equation}로그형태는 감소하는 마진 복잡도를 반영한다. 형식 실패에서 $`\alpha_3 = 0.05`$로 추정된다.
결합 모델:
\begin{equation}
Q_{\text{eff}} = Q(S) \cdot (1 - P_{\text{role}} - P_{\text{complexity}} - P_{\text{perceived}})
\end{equation}제안 4. $`S^*`$에서 연속성을 위해 $`a = Q_{\max}/S^*= 1.96`$이 필요하다.
완전 모델:
\begin{equation}
Q_{\text{eff}} = Q(S) \cdot \eta \cdot (1 - P_{\text{role}} - P_{\text{complexity}} - P_{\text{perceived}})
\end{equation}| 버전 | ArXiv 원문 PDF 보기
📊 논문 시각자료 (Figures)
감사의 말씀이 글의 저작권은 연구하신 과학자분들께 있으며, 인류 문명 발전에 공헌해주신 노고에 감사를 드립니다.관련 게시글검색 시작검색어를 입력하세요
검색 중...
검색 결과 없음다른 검색어로 시도해보세요
↑↓
이동
↵
선택
ESC
닫기
⌘K
단축키
목차
点击标题快速跳转
|
|---|