LLMize 대형 언어 모델 기반 수치 최적화 프레임워크
📝 원문 정보
- Title: LLMize: A Framework for Large Language Model-Based Numerical Optimization
- ArXiv ID: 2601.00874
- 발행일: 2025-12-30
- 저자: M. Rizki Oktavian
📝 초록 (Abstract)
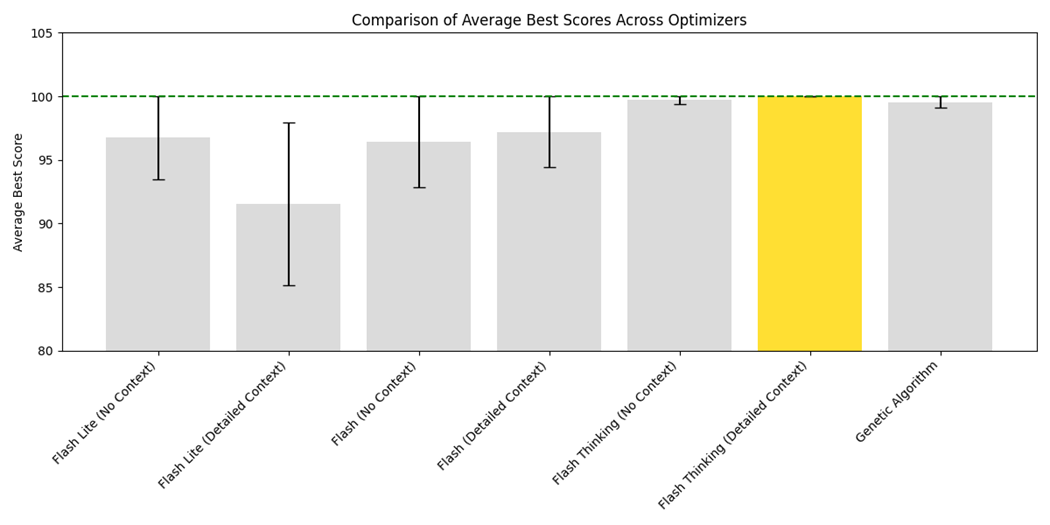
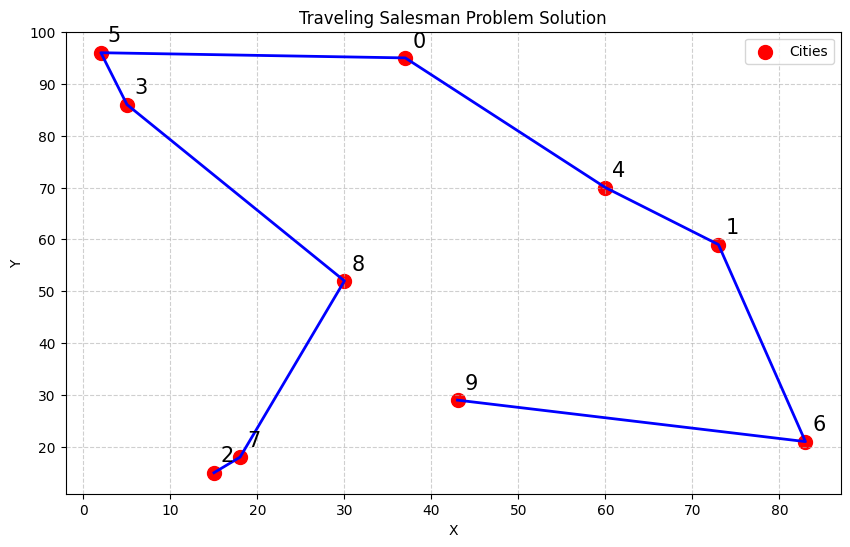
대형 언어 모델(LLM)이 전통적인 언어 작업을 넘어 강력한 추론 능력을 보이며 수치 최적화에도 활용될 가능성이 제시되고 있다. 본 논문은 LLM 기반 최적화를 구현하는 오픈소스 파이썬 프레임워크인 LLMize를 소개한다. LLMize는 후보 해를 자연어로 생성하고, 외부 목적 함수로 평가한 뒤, 해‑점수 피드백을 이용해 반복적으로 개선하는 블랙박스 최적화 과정을 제공한다. 프레임워크는 Prompt 기반 최적화(OPRO)와 진화 알고리즘·시뮬레이티드 어닐링을 차용한 하이브리드 방식 등 여러 전략을 지원한다. 자연어로 제약, 규칙, 도메인 지식을 직접 주입할 수 있어 복잡한 제약을 수학적으로 모델링하기 어려운 문제도 전문가 수준의 프로그래밍 없이 정의할 수 있다. LLMize는 볼록 최적화, 선형 계획법, 외판원 문제, 신경망 하이퍼파라미터 튜닝, 핵연료 격자 최적화 등에 대해 평가되었다. 결과는 단순 문제에서는 기존 고전 솔버에 뒤처지지만, 제약과 휴리스틱을 명시하기 어려운 복합 도메인에서는 실용적이고 접근성 높은 대안을 제공함을 보여준다.💡 논문 핵심 해설 (Deep Analysis)

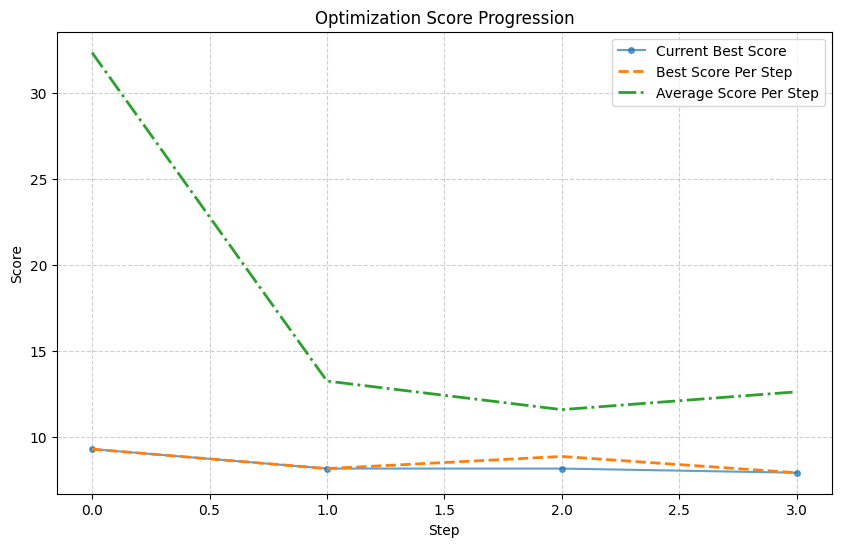
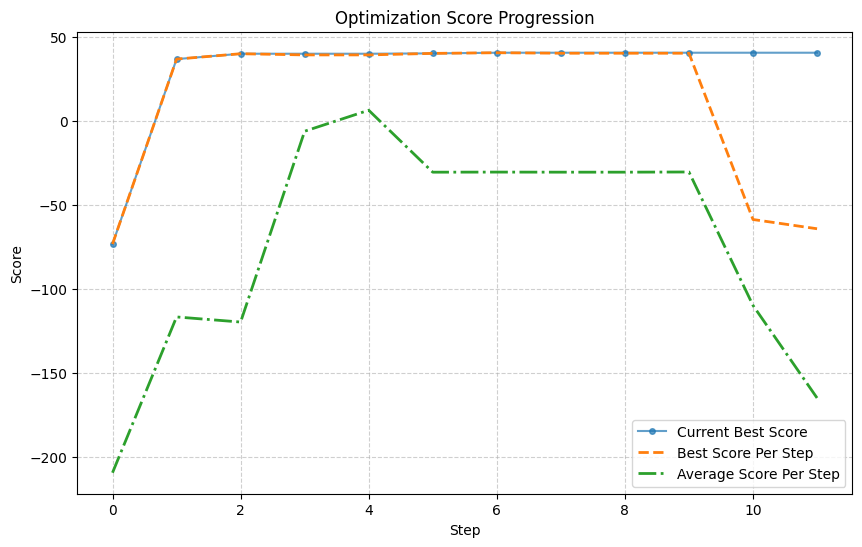
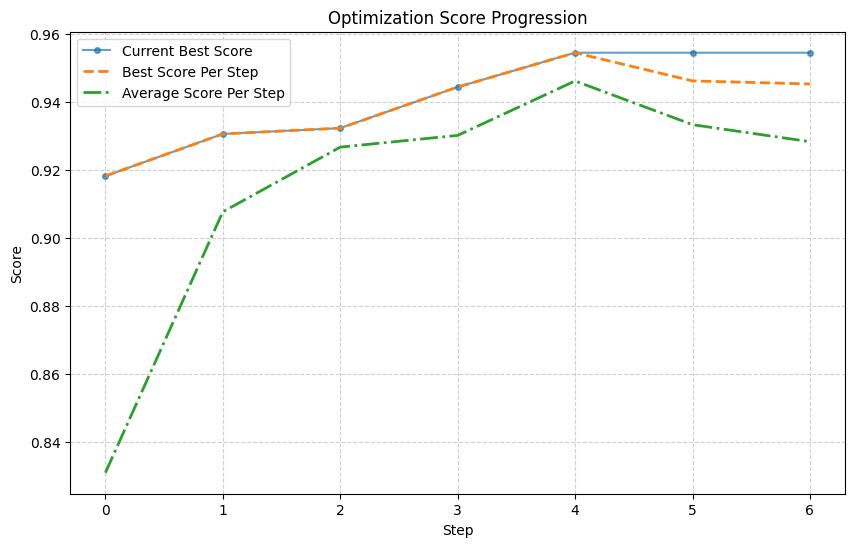
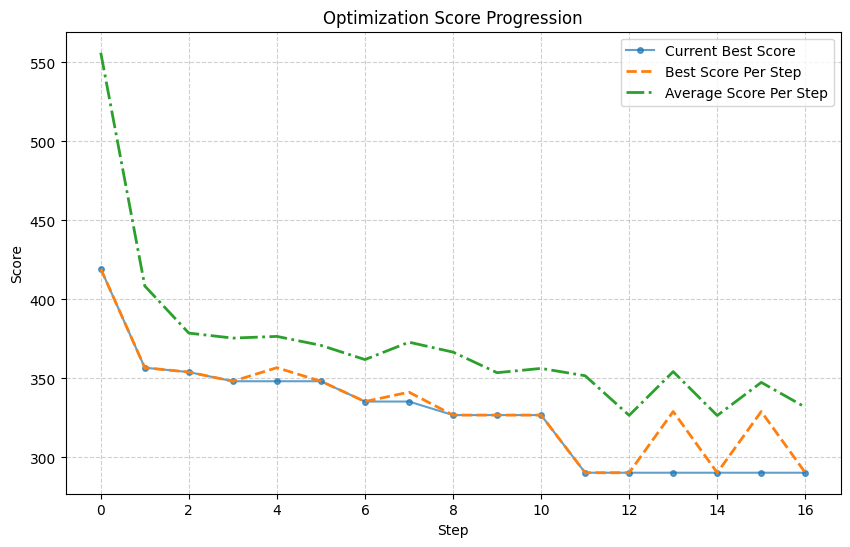
LLMize가 제공하는 두 가지 주요 전략, OPRO와 하이브리드 방식은 각각 장단점이 있다. OPRO는 순수하게 LLM의 생성 능력에 의존해 탐색 공간을 넓히지만, 탐색 효율성이 낮아 복잡한 고차원 문제에서는 수렴 속도가 느릴 수 있다. 반면, 하이브리드 방식은 진화 연산자(교배, 돌연변이)와 시뮬레이티드 어닐링의 온도 스케줄을 자연어로 기술하고, LLM이 이를 해석·실행하도록 함으로써 전통적인 메타휴리스틱의 탐색 강도와 LLM의 도메인 지식 활용을 결합한다. 실험 결과는 이러한 혼합 접근법이 특히 제약이 복잡하고 목표 함수가 블랙박스 형태인 핵연료 격자 최적화와 같은 분야에서 유의미한 성능 향상을 보였음을 보여준다.
또한 LLMize의 가장 큰 강점은 “제약과 규칙을 자연어로 주입한다”는 점이다. 전통적인 수학적 모델링에서는 비선형 제약, 논리적 규칙, 불확실성 등을 정형화하기 위해 복잡한 수식이나 추가 변수 도입이 필요하지만, LLM은 텍스트 기반 설명을 그대로 이해하고 이를 후보 해 생성 과정에 반영한다. 예를 들어, “핵연료 핀은 서로 겹치지 않아야 한다”는 문장을 프롬프트에 포함시키면, LLM은 겹침을 피하도록 레이아웃을 제안한다. 이는 도메인 전문가가 코딩 없이도 최적화 문제를 정의할 수 있게 하여, 연구·산업 현장에서의 진입 장벽을 크게 낮춘다.
하지만 한계도 명확하다. 현재 LLM의 토큰 길이 제한과 추론 비용 때문에 대규모 변수 수를 가진 문제에서는 실용성이 떨어진다. 또한 LLM이 생성한 해는 종종 비정형(예: 문자열, 비표준 포맷) 형태이므로, 파싱 및 검증 단계에서 추가적인 엔지니어링이 필요하다. 마지막으로, LLM 자체가 확률적 모델이기 때문에 동일한 프롬프트에 대해 매 실행마다 다른 해를 반환한다는 점은 재현성 측면에서 고민거리가 된다. 이러한 문제들을 해결하기 위해서는 프롬프트 엔지니어링 자동화, 토큰 효율화, 그리고 LLM 출력 검증 메커니즘이 추가로 연구되어야 할 것이다.
요약하면, LLMize는 LLM의 자연어 이해·생성 능력을 최적화 엔진으로 전환함으로써, 복잡한 제약과 도메인 지식을 손쉽게 통합할 수 있는 새로운 패러다임을 제시한다. 현재는 간단한 문제에서 고전 솔버에 뒤처지지만, 인간이 정의하기 어려운 복합 제약을 갖는 실세계 문제에서는 실용적인 대안이 될 가능성이 크다. 향후 LLM 모델의 규모와 효율성이 개선되면, LLM 기반 최적화가 전통적인 수치 최적화와 경쟁하거나 보완하는 영역이 확대될 것으로 기대된다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리