무작위 다중화: 채널 독립 고성능 전송 기술

2025년 12월 30일

읽는 시간: 4 분

...

#Information Theory #Computer Science

📝 원문 정보

Title: Random Multiplexing
ArXiv ID: 2512.24087
발행일: 2025-12-30
저자: Lei Liu, Yuhao Chi, Shunqi Huang, Zhaoyang Zhang

📝 초록 (Abstract)

무선 통신이 전통적인 다중경로 환경에서 무인항공기와 같은 고이동 시나리오로 확대됨에 따라 다중화 기법도 진화하고 있다. 기존의 단일반송파 주파수 영역 등화(SC‑FDE)와 정교한 직교 주파수 분할 다중화(OFDM)는 Toeplitz 구조의 다중경로 채널 행렬을 이용해 채널을 대각화하거나 희소화함으로써 저복잡도 검출을 가능하게 했다. 그러나 이러한 구조에 대한 의존성은 실제 동적 환경에서의 견고성을 크게 제한한다. 본 논문은 물리적 채널과 무관하게 동작하는 무작위 다중화(Random Multiplexing) 기법을 연구한다. 무작위 변환 영역에서 등방성 입력 채널 행렬을 구성함으로써 전송 신호에 대한 통계적 페이딩 채널 에르고딕성을 달성한다. 또한, 임의의 노름 제한 및 스펙트럼 수렴 채널 행렬에 대해 고유 고정점 가정 하에 AMP‑계열 검출기의 복제 MAP 비트 오류율(BER) 최적성을 보장한다. 본 연구에서는 시간 영역 채널의 희소성과 등방성 입력을 동시에 활용하는 저복잡도 교차 영역 메모리 AMP(CD‑MAMP) 검출기를 제안한다. 복제 MAP BER을 최소화하고 복제 제약 용량을 최대화하기 위한 최적 전력 할당식을 도출하고, 최적 코딩 원칙 및 CD‑MAMP 검출기의 복제 제약 용량 최적성을 분석한다. 마지막으로 무작위 다중화가 다양한 무선 응용 분야에 적용될 수 있음을 탐색하고, 수치 실험을 통해 이론적 결과를 검증한다.

💡 논문 핵심 해설 (Deep Analysis)

본 논문이 제시하는 “무작위 다중화”는 기존 OFDM·SC‑FDE가 활용하는 Toeplitz‑구조 혹은 OTFS·AFDM이 전제하는 이중 선택성(doubly‑selective) 채널 특성에 얽매이지 않는다. 전통적인 방법들은 채널 행렬을 대각화하거나 희소화함으로써 복소수 FFT/ IFFT 연산만으로 저복잡도 검출을 구현한다. 그러나 실제 고이동 환경에서는 채널 응답이 급격히 변하고, 다중 경로가 비정형적인 구조를 띠며, 스펙트럼이 비정상적으로 확산되는 경우가 빈번하다. 이러한 상황에서 Toeplitz 가정이 깨지면 OFDM·SC‑FDE의 성능은 급격히 저하되고, OTFS·AFDM도 채널 매핑 단계에서 큰 손실을 입는다.

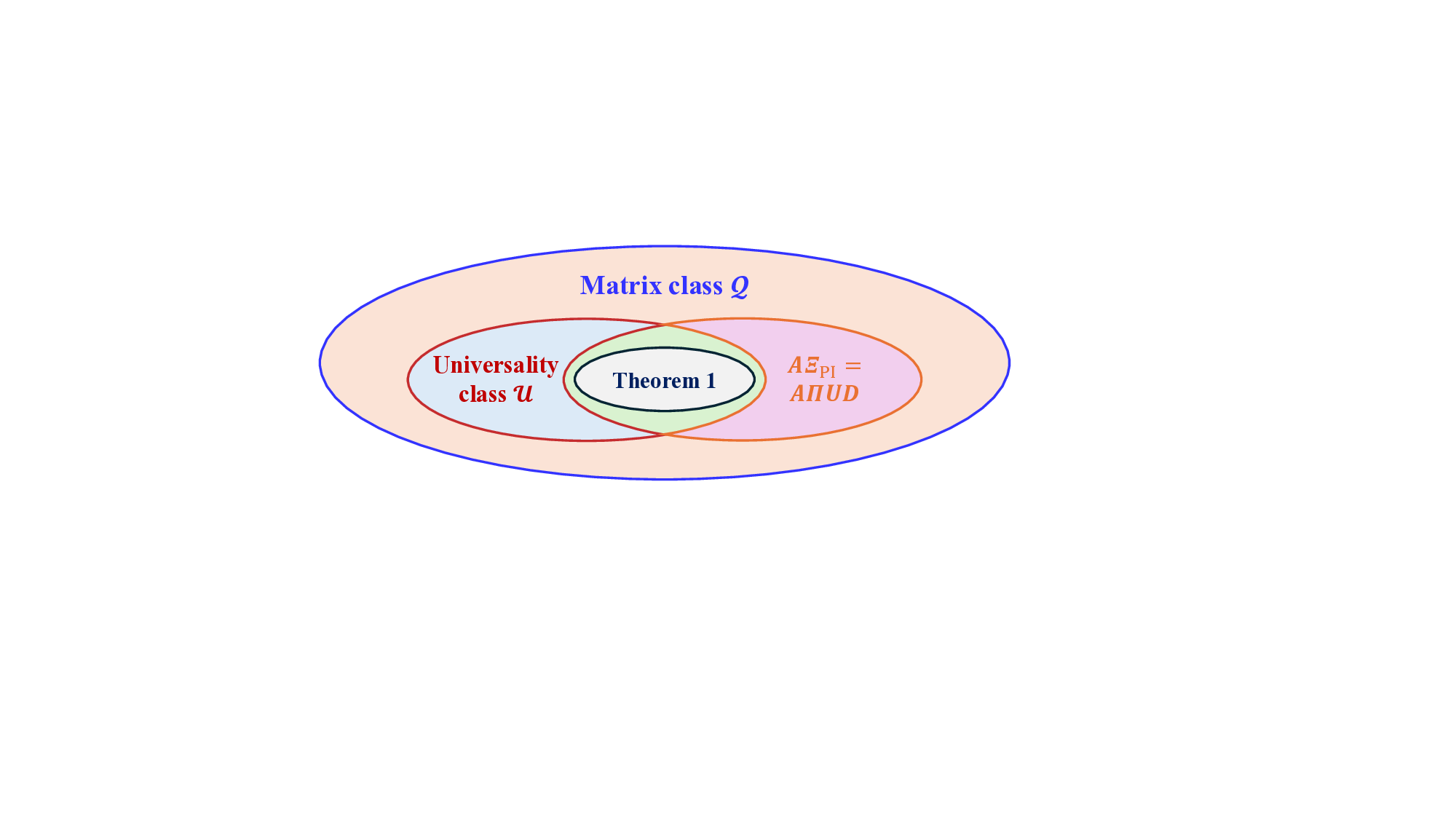
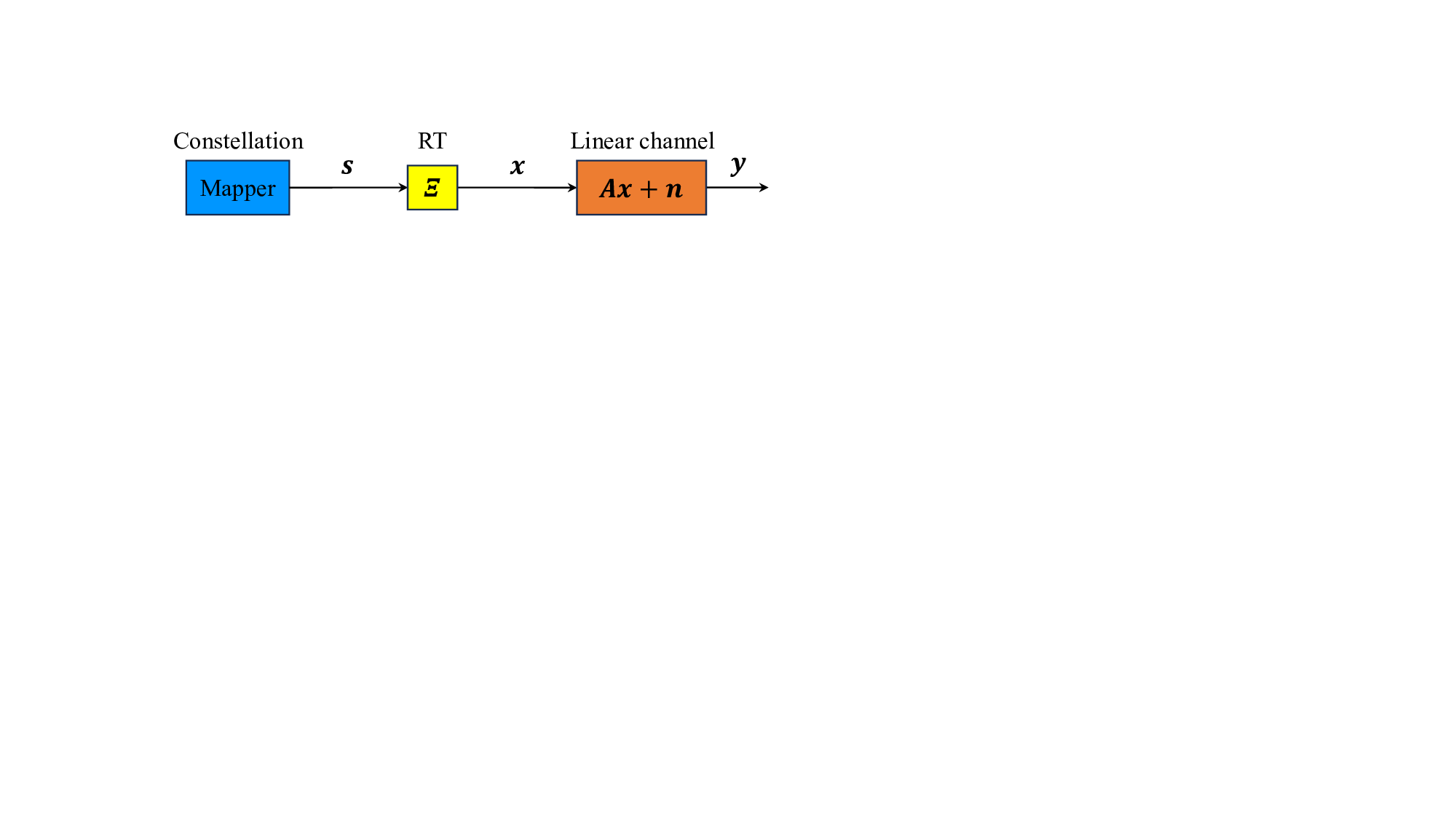
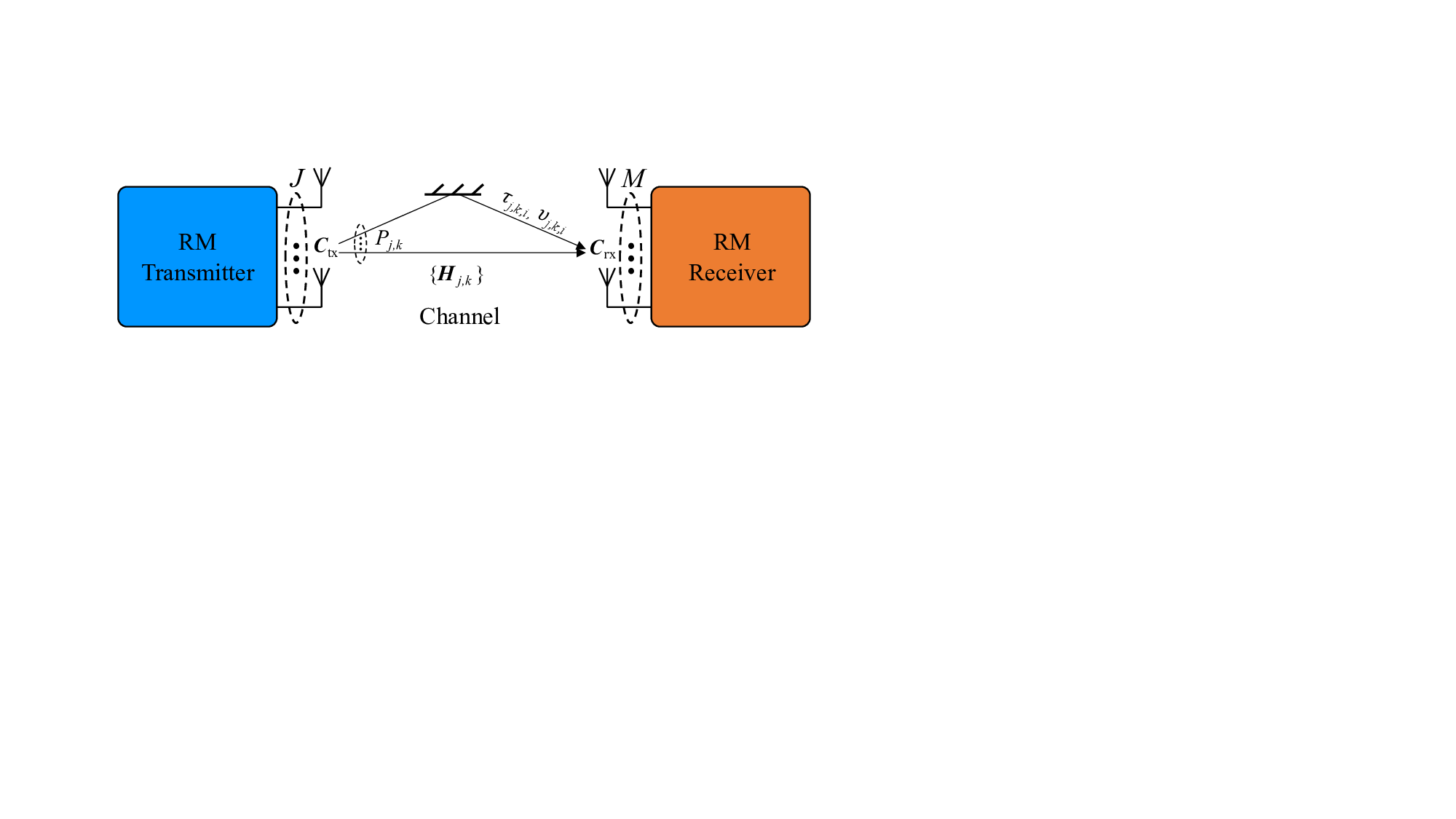
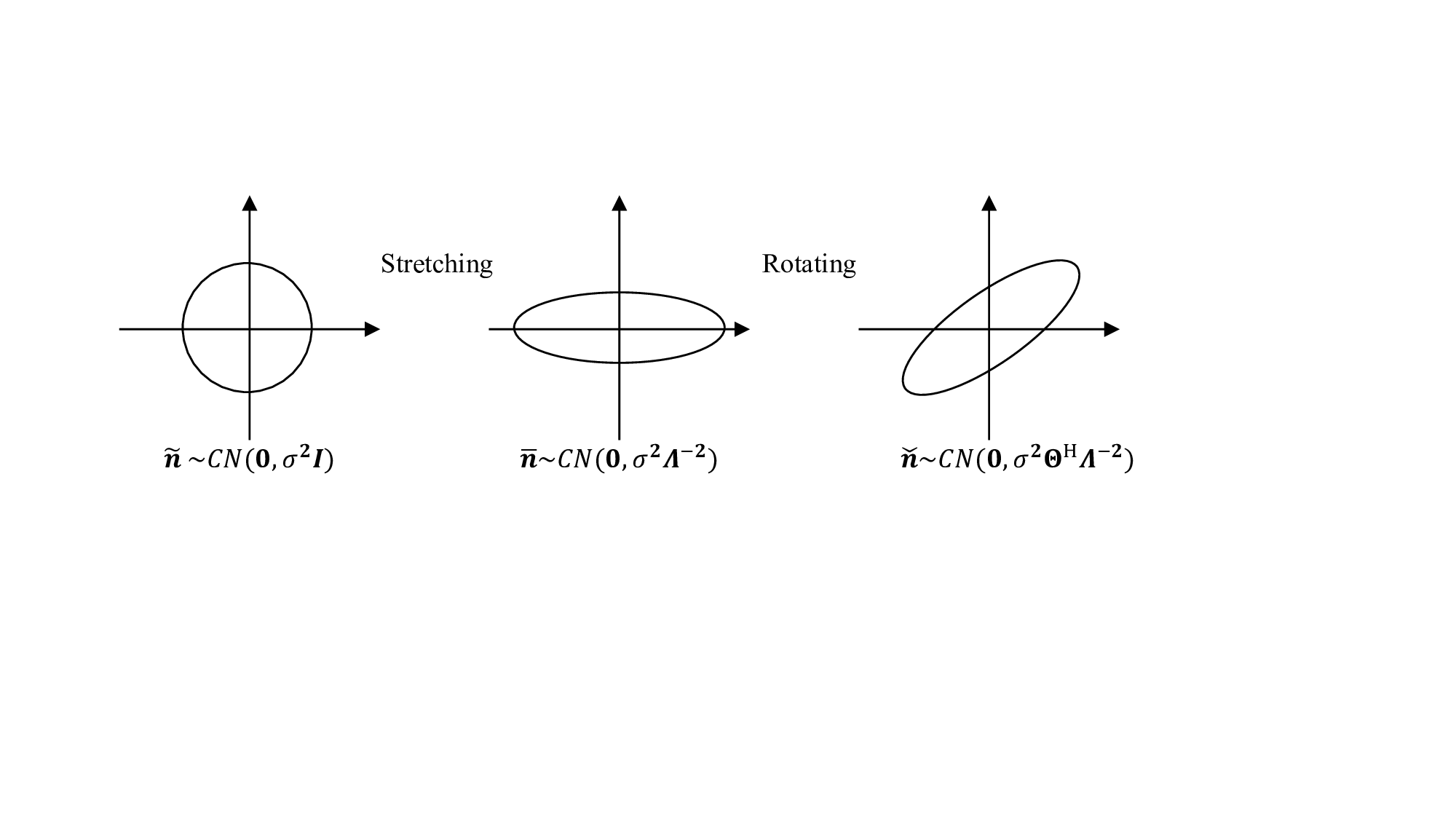
무작위 다중화는 이러한 구조적 의존성을 근본적으로 제거한다. 송신 측에서 신호를 무작위 선형 변환(예: 고차원 가우시안 행렬 또는 Haar 무작위 유니터리 행렬)으로 사전 변조하고, 수신 측에서는 동일 변환의 역을 이용해 복원한다. 이 과정에서 채널 행렬 H와 무작위 변환 행렬 Φ가 결합된 등가 행렬 A = H Φ가 “입력 등방성(isotropic)” 특성을 갖게 된다. 즉, A는 입력 신호의 방향에 무관하게 동일한 통계적 분포를 유지하므로, 복제 이론(replica method) 하에서 “채널 에르고딕성”을 보장한다.

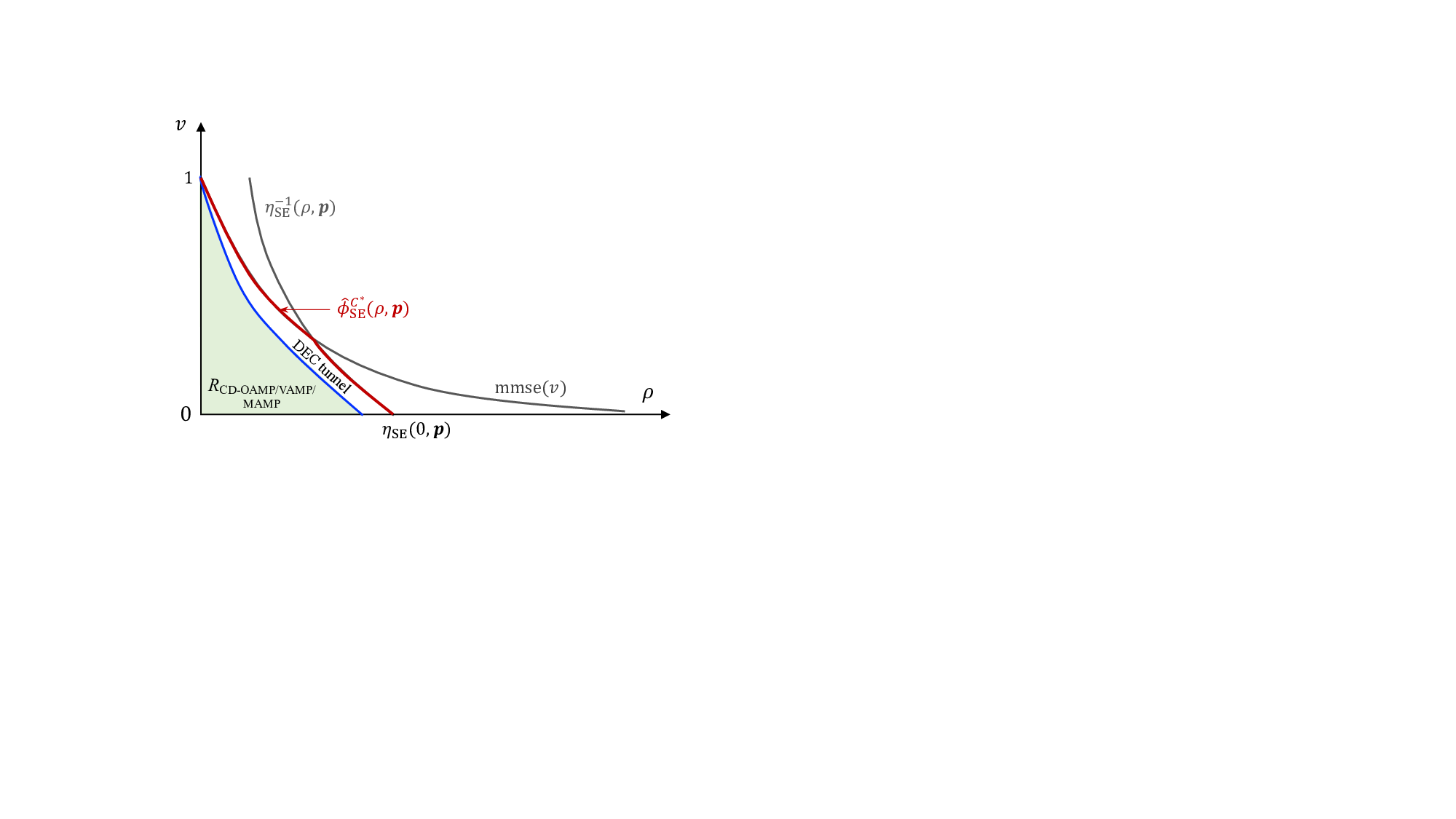
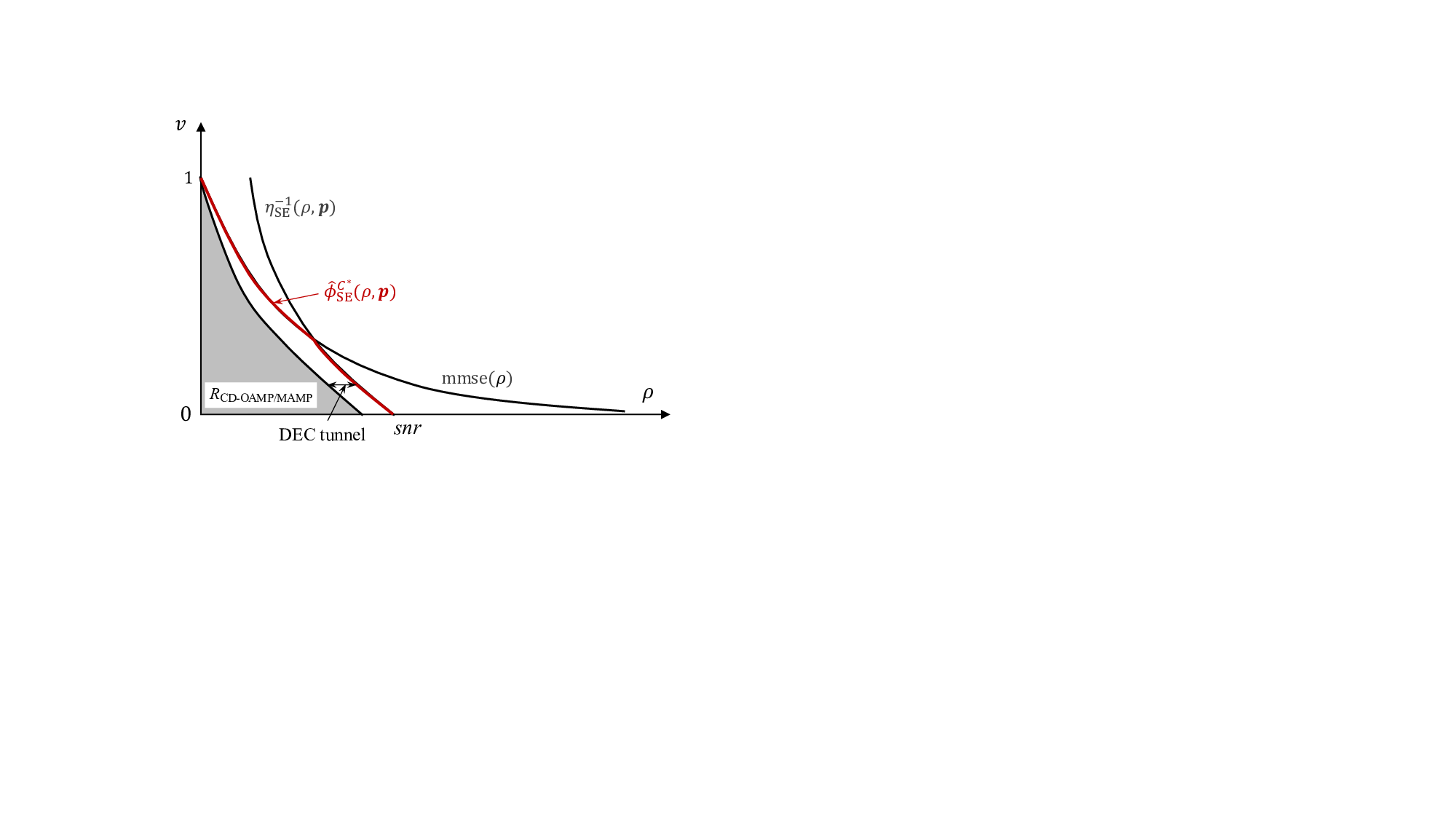
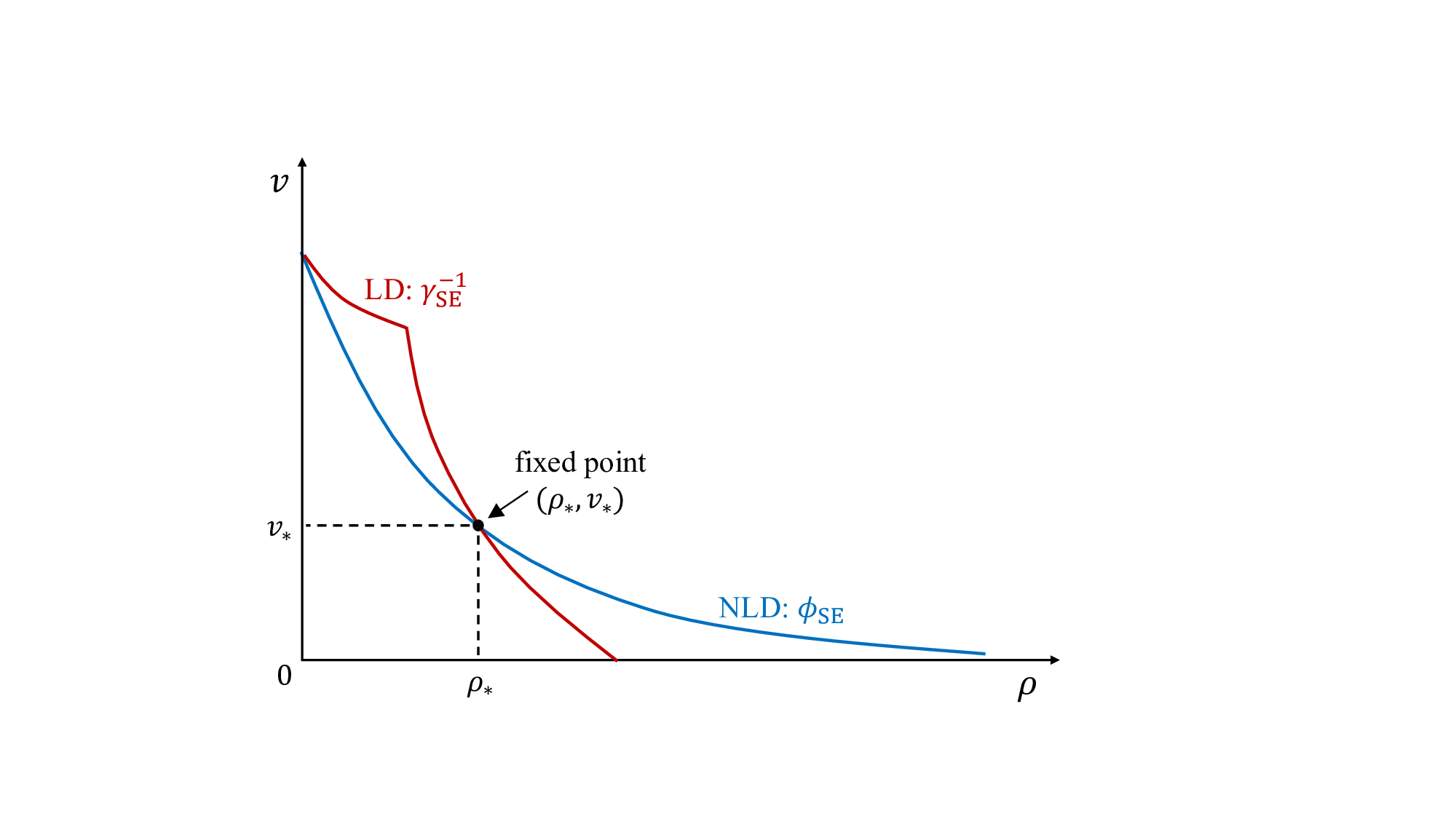
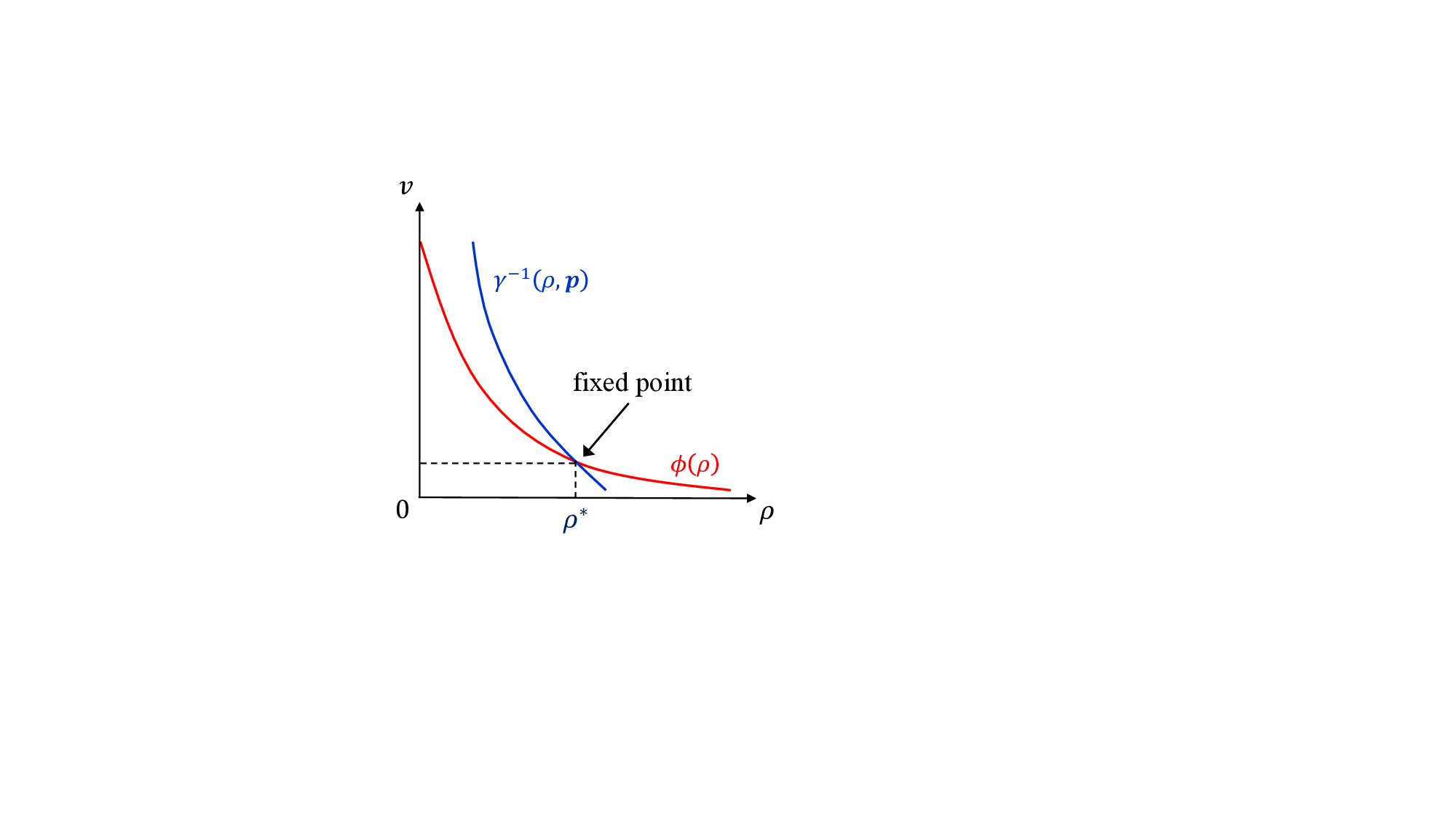
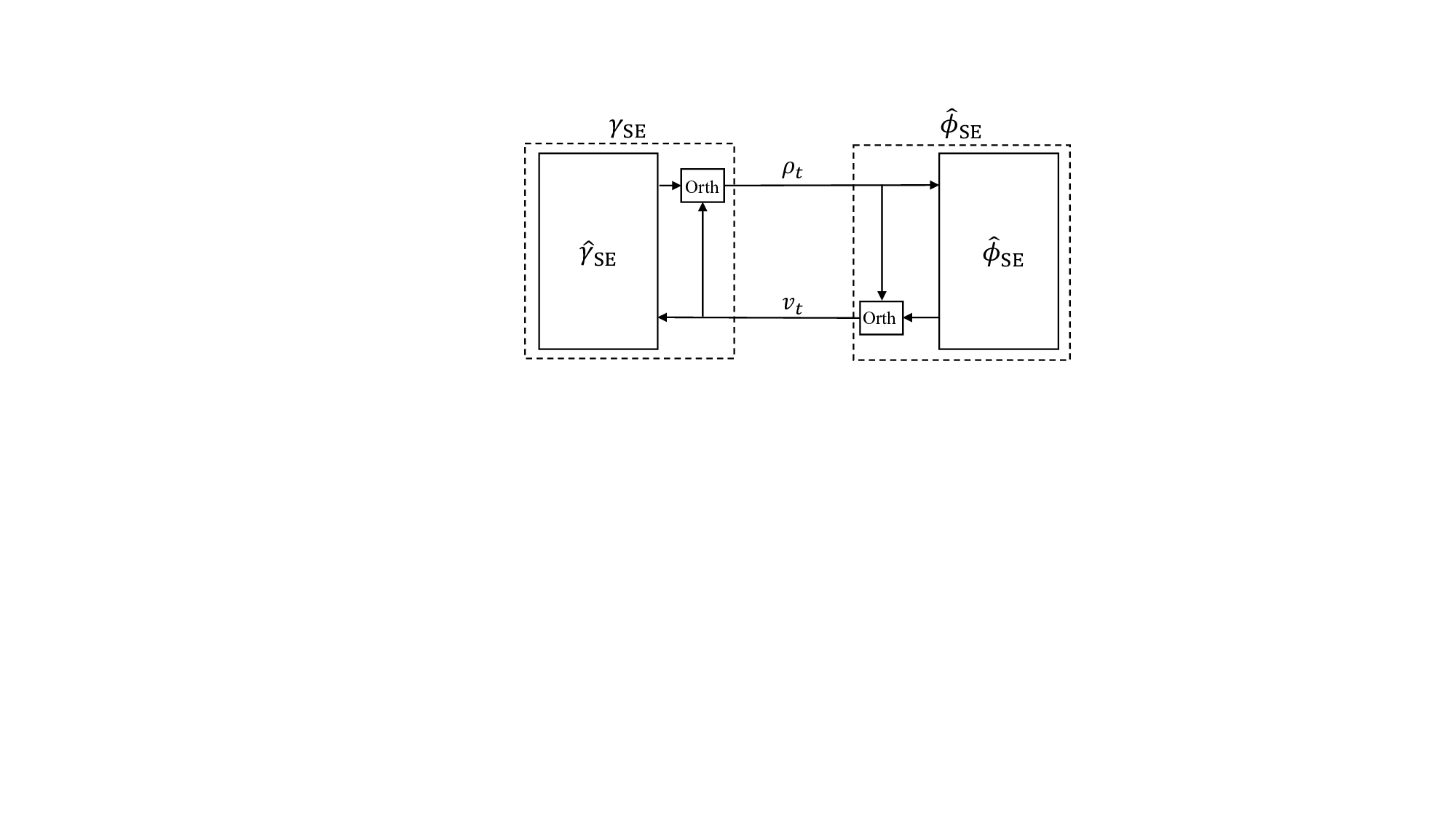
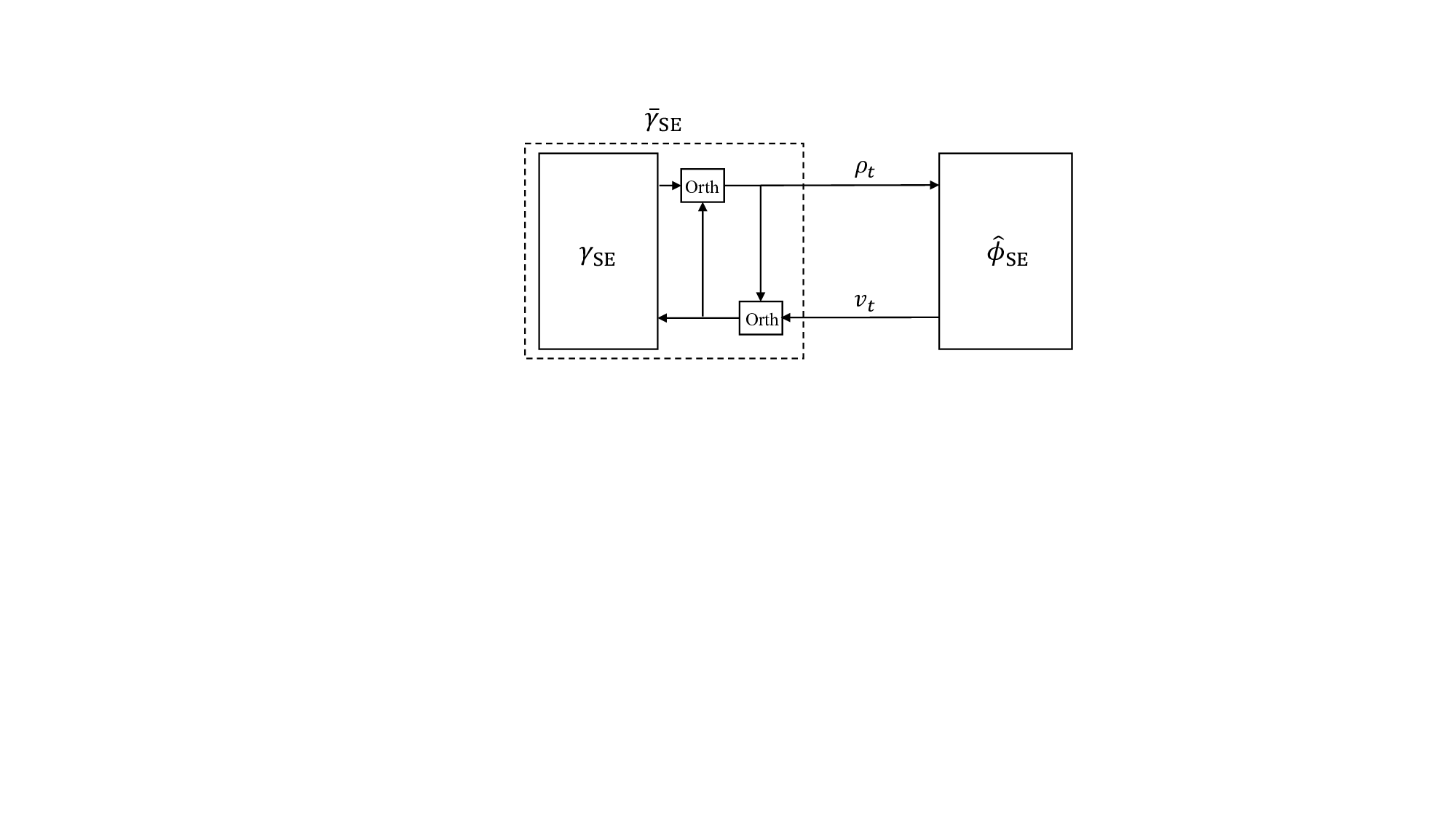
이러한 등방성은 AMP(Approximate Message Passing) 계열 검출기의 상태 진화 방정식(state evolution)이 채널 고유값 스펙트럼에만 의존하게 만든다. 논문은 “고유 고정점 가정(unique fixed‑point assumption)”을 전제로, 임의의 노름 제한(norm‑bounded) 및 스펙트럼 수렴(spectrally convergent) 채널에 대해 복제 MAP BER이 AMP의 최적점과 일치함을 증명한다. 이는 기존에 구조적 제약을 받아야 했던 AMP의 적용 범위를 크게 확장한다는 의미다.

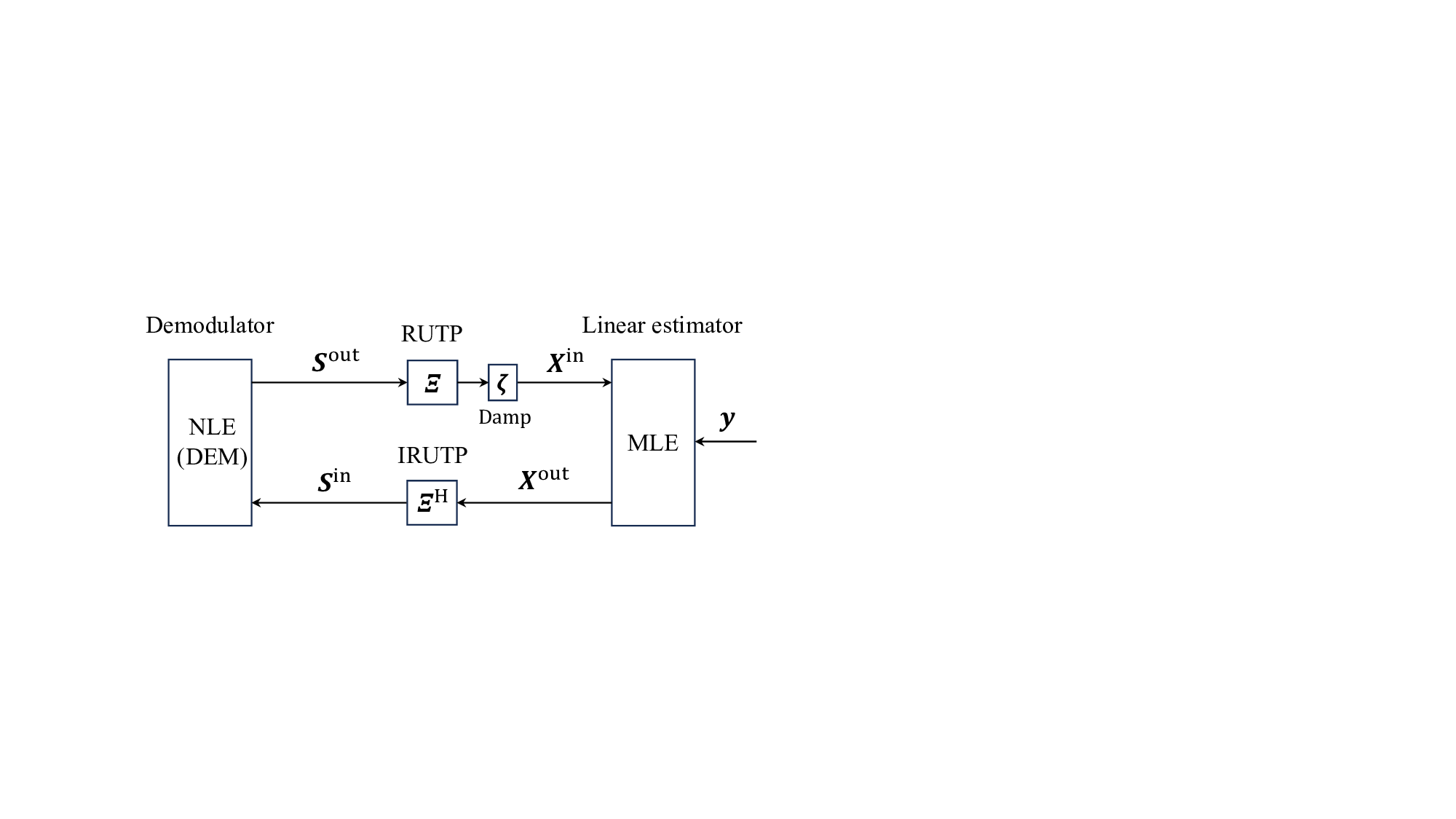
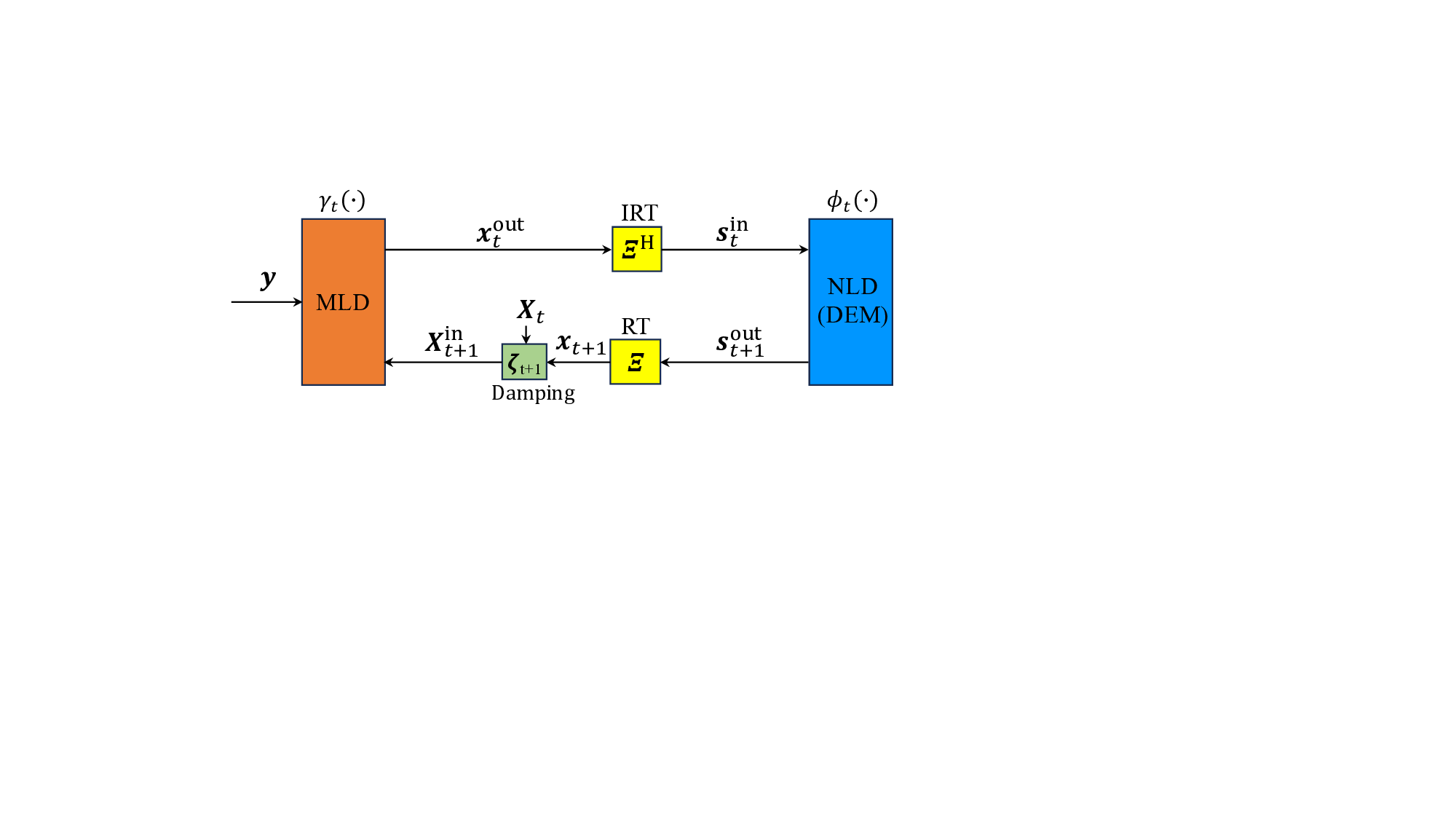
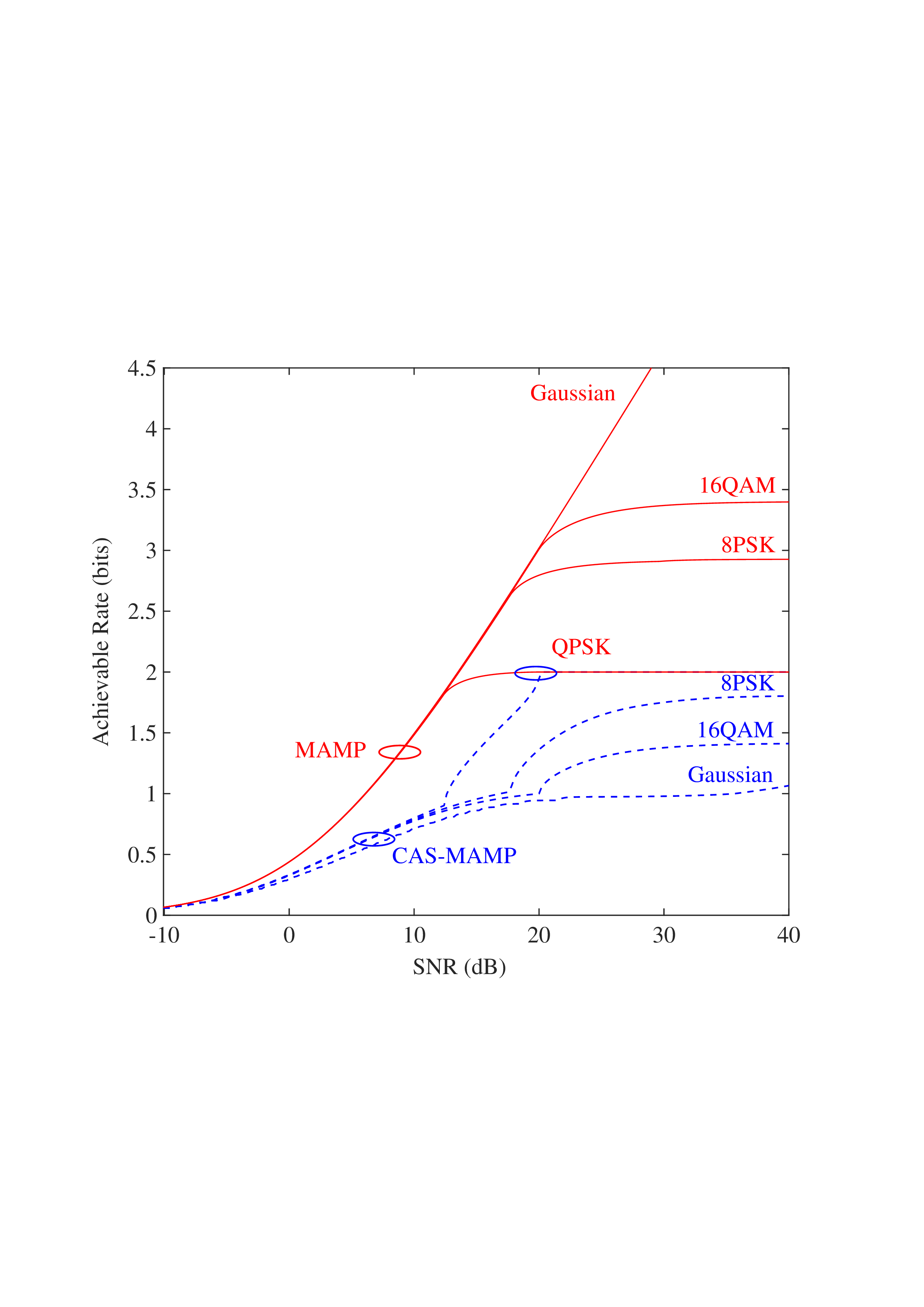
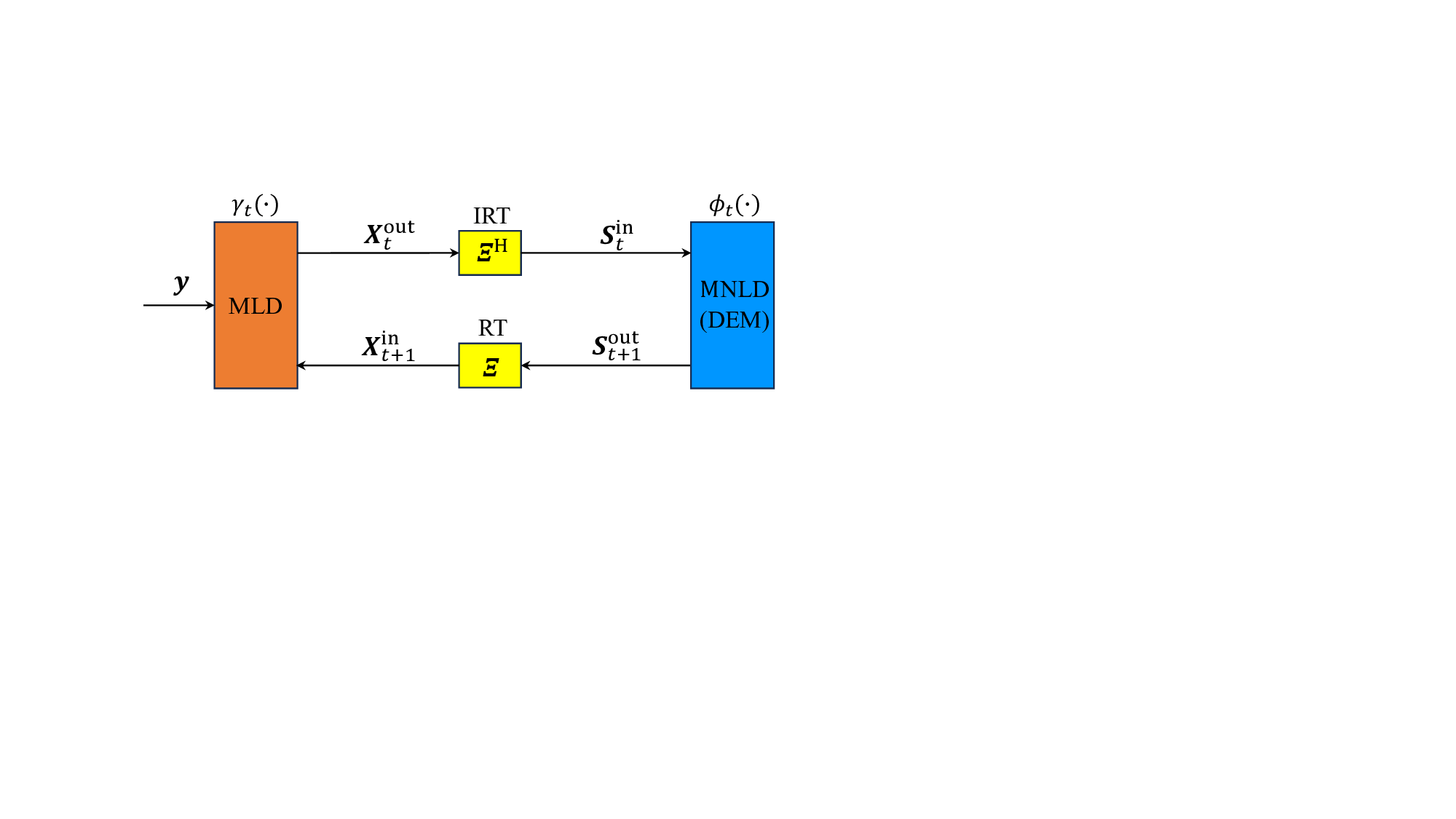
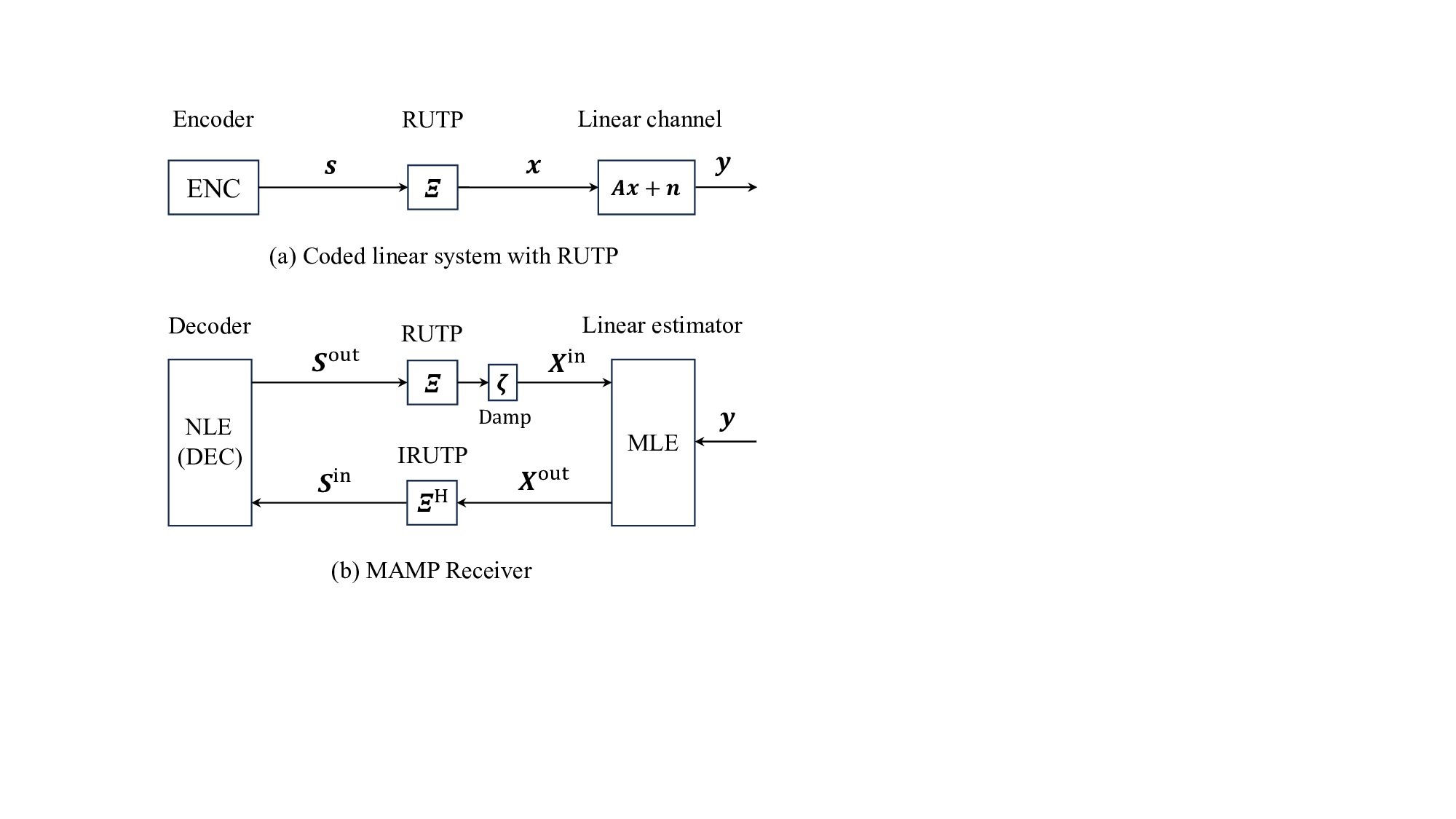
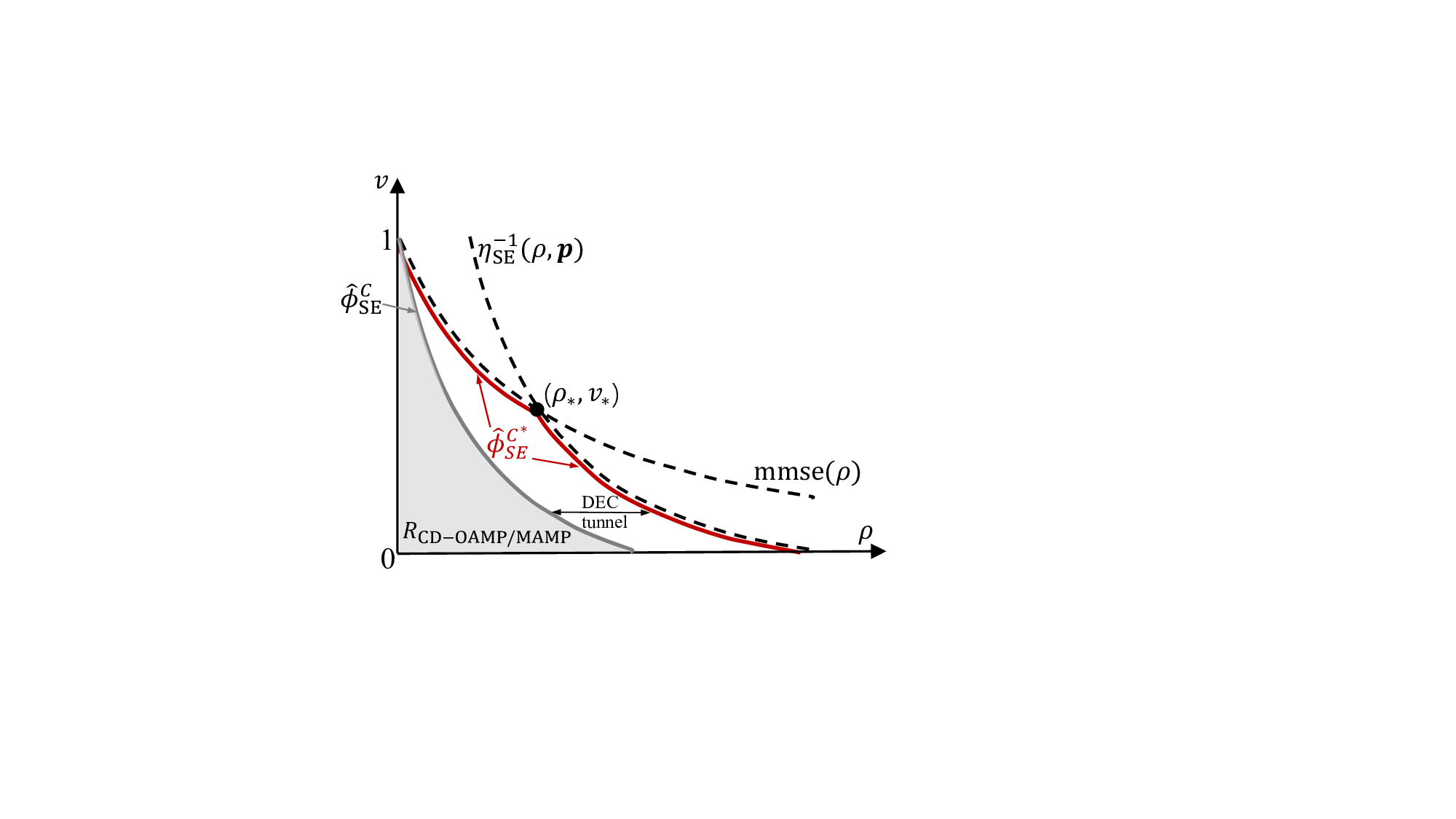
특히 저복잡도 구현을 위해 제안된 CD‑MAMP(detector) 는 두 가지 핵심 아이디어를 결합한다. 첫째, 실제 무선 채널은 시간 영역에서 매우 희소(sparse)하다는 점을 이용해 메시지 전달을 “교차 영역(cross‑domain)”으로 전이시킨다. 둘째, 무작위 변환에 의해 입력이 등방성을 갖게 되므로, 메시지 업데이트 과정에서 복잡한 행렬 곱셈 대신 스칼라 형태의 “가우시안 등가 채널” 모델을 사용할 수 있다. 결과적으로 연산 복잡도는 O(N log N) 수준으로 유지되면서도, 성능은 복제 MAP 한계에 근접한다.

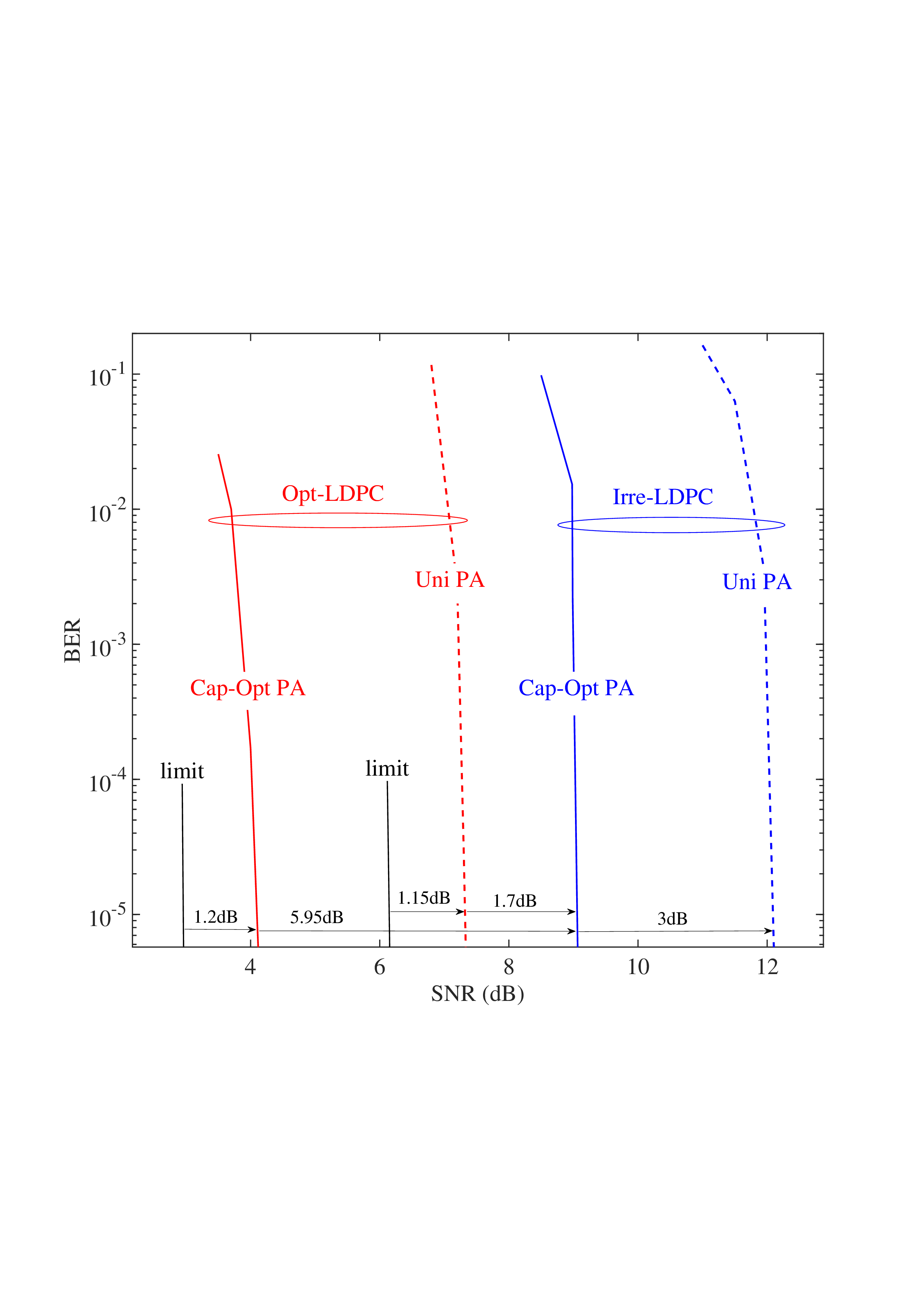
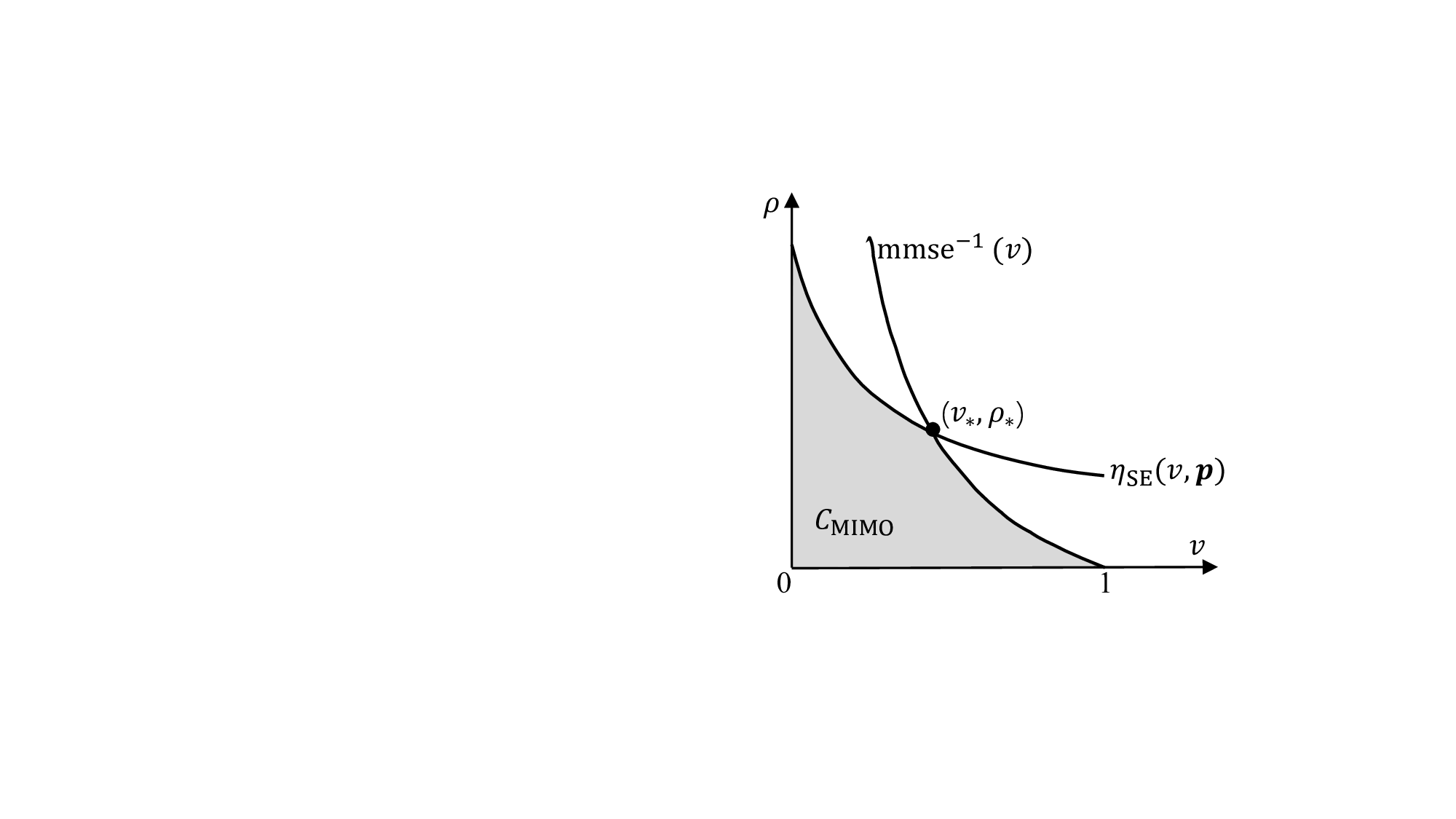
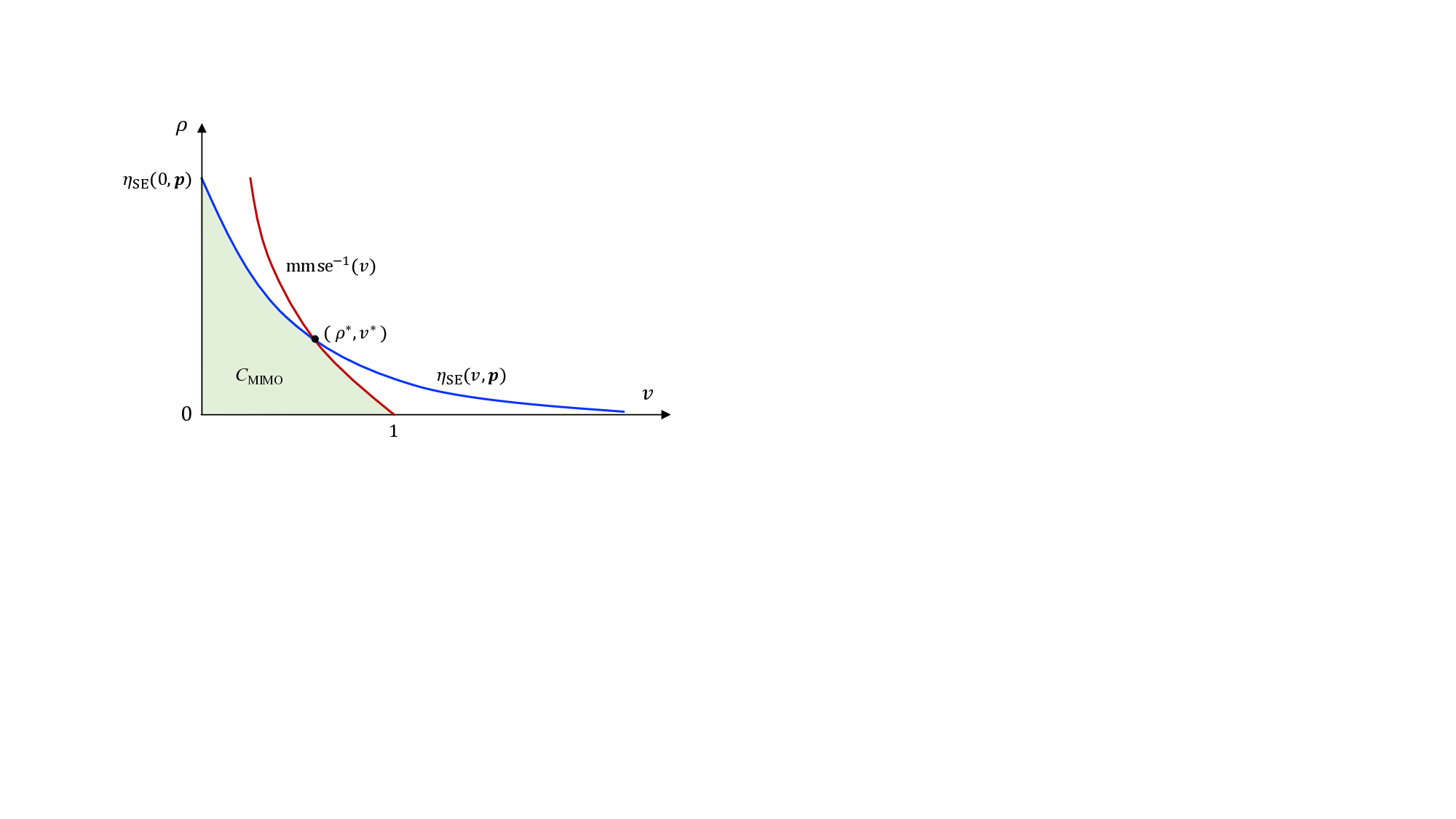
전력 할당 측면에서는 복제 MAP BER을 최소화하는 “베르누이 최적 전력 배분(Bernoulli optimal power allocation)”과, 복제 제약 용량을 최대화하는 “워터‑필링 형태의 최적 배분”을 각각 유도한다. 이때 채널 고유값 분포와 무작위 변환의 스케일 파라미터가 핵심 변수로 작용한다. 또한, 논문은 “최적 코딩 원칙(optimal coding principle)”을 제시하여, 등방성 입력에 맞는 코덱 설계가 복제 제약 용량에 도달하도록 한다.

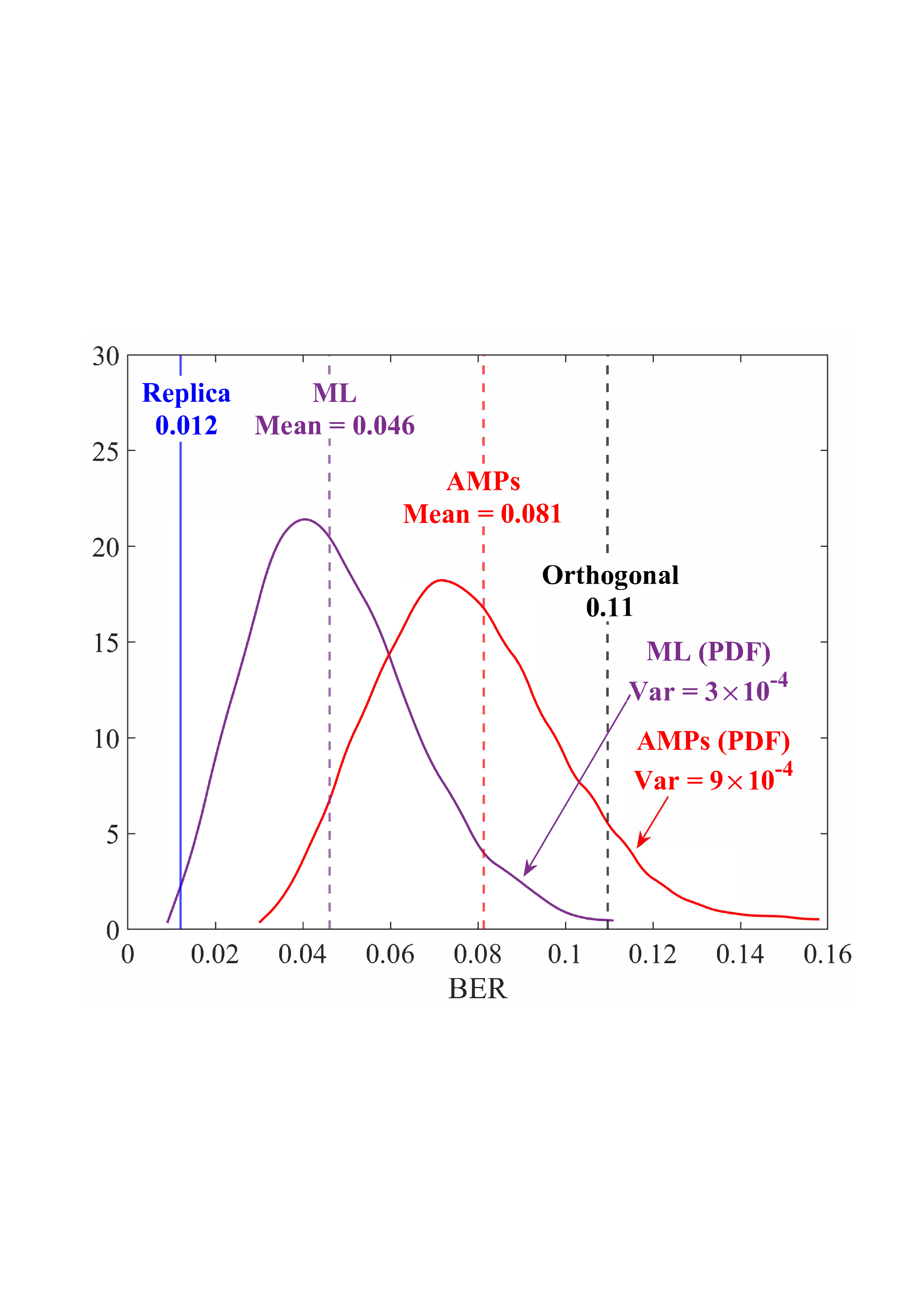
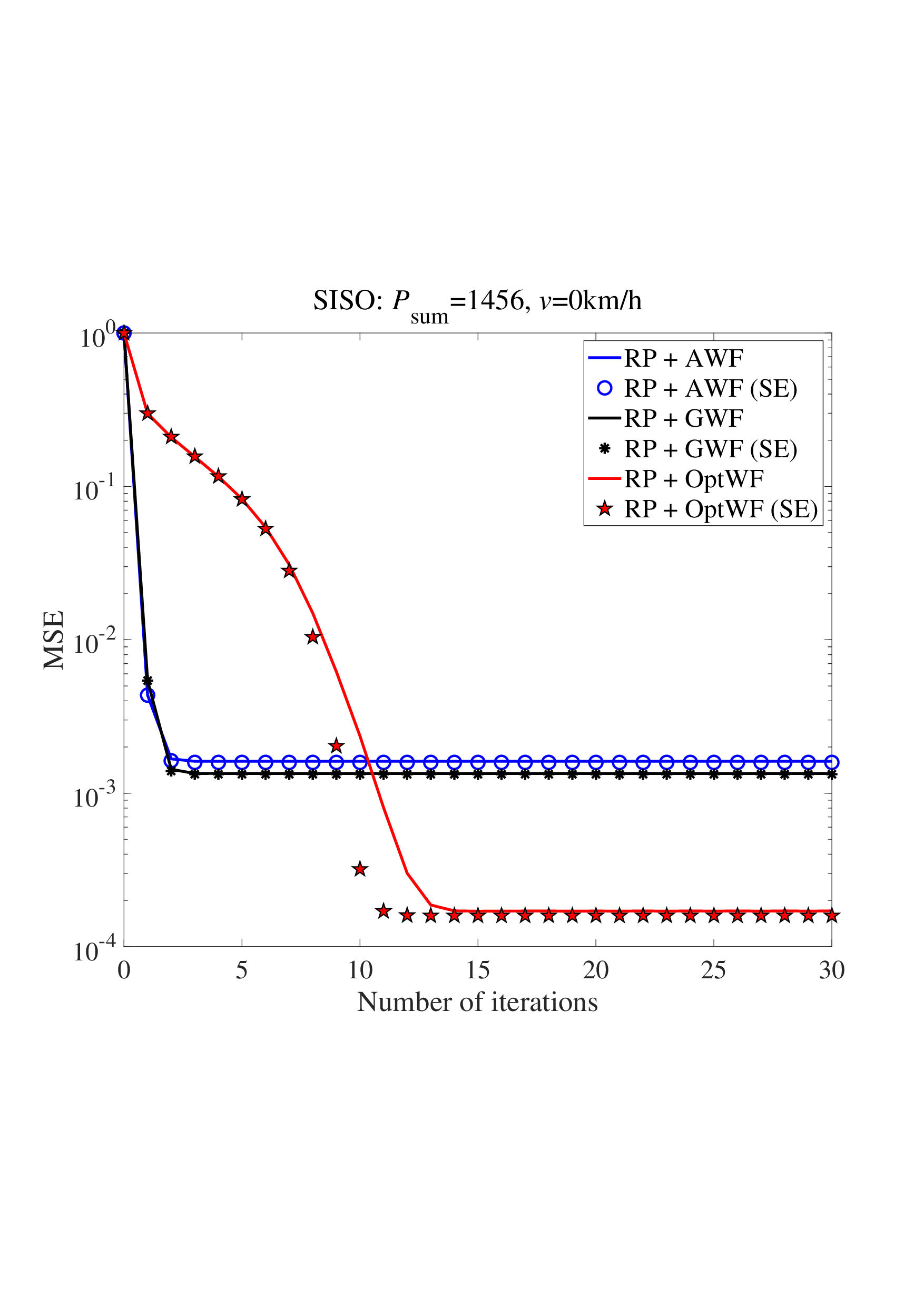
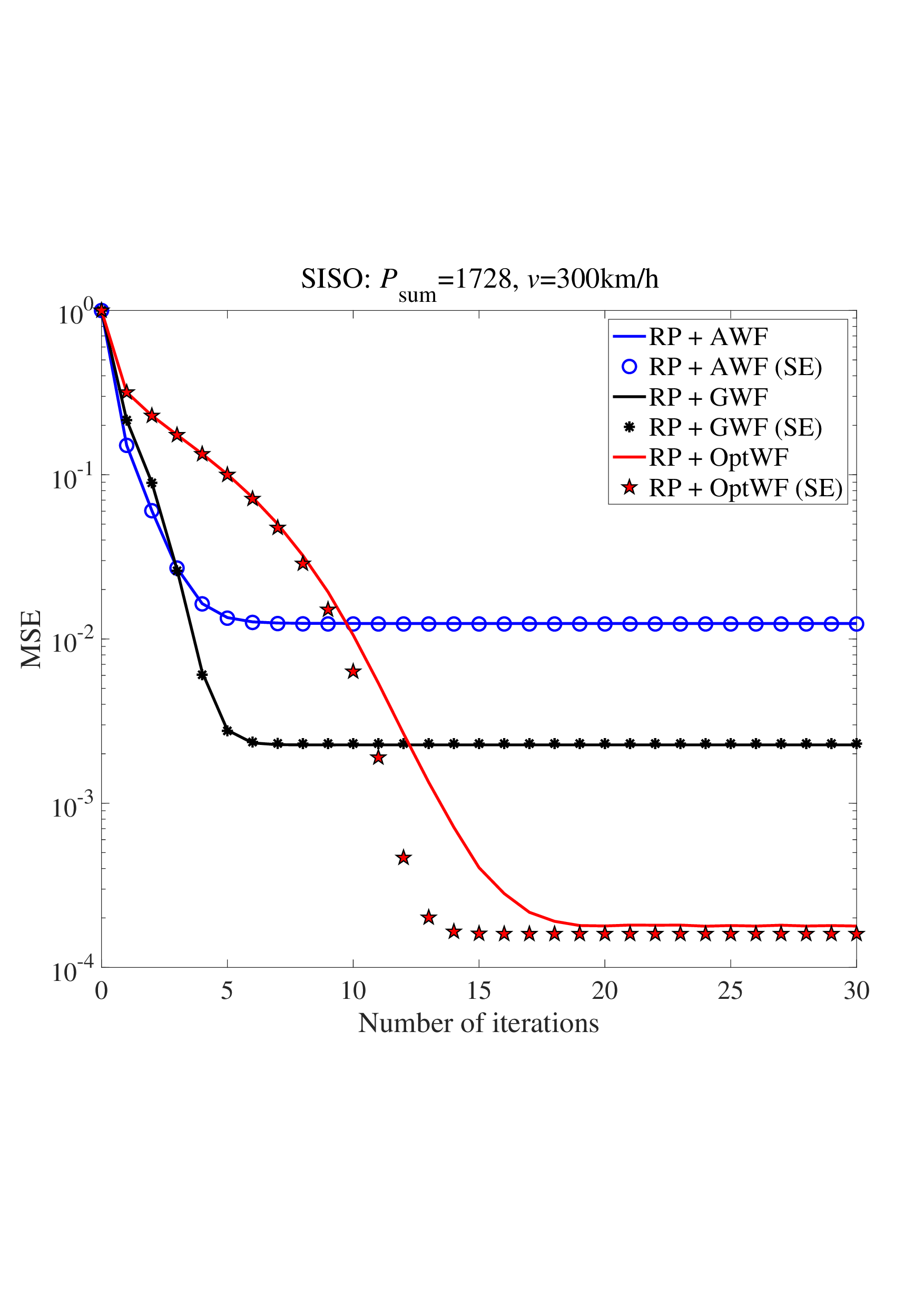
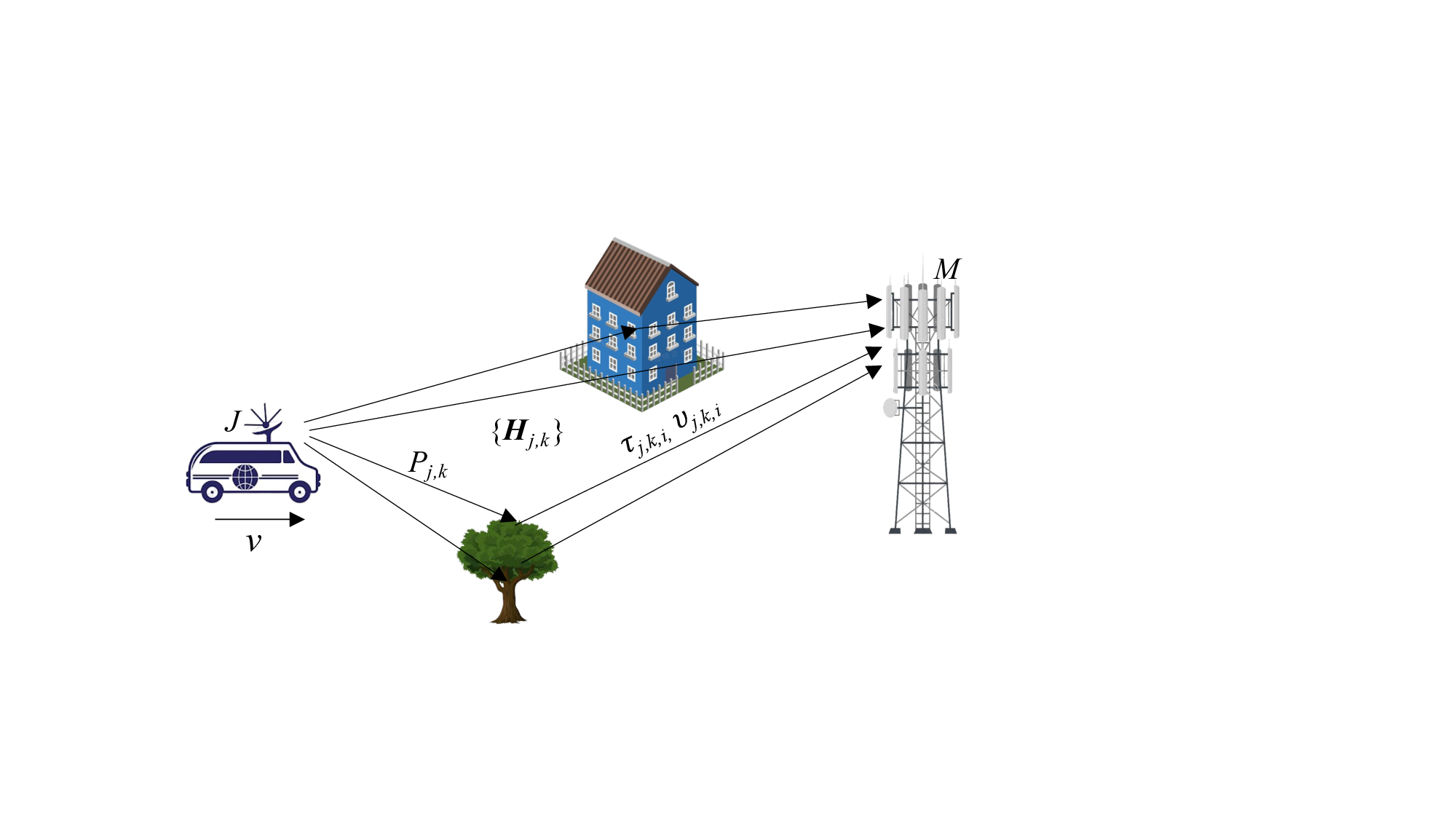
마지막으로 무작위 다중화는 위성 통신, UAV 네트워크, 밀리미터파(mmWave) 및 THz 통신 등, 채널 특성이 급변하거나 사전 모델링이 어려운 다양한 시나리오에 적용 가능함을 시뮬레이션을 통해 입증한다. 실험 결과는 전통적 구조 기반 기법 대비 2 ~ 5 dB 수준의 SNR 이득을 보여주며, 특히 고속 이동성(> 300 km/h) 상황에서 BER이 급격히 상승하는 현상을 효과적으로 억제한다.

요약하면, 무작위 다중화는 “채널 독립성”이라는 새로운 패러다임을 도입함으로써, 기존 다중화 기법이 직면한 구조적 한계를 극복하고, AMP 기반 저복잡도 검출과 최적 전력·코딩 설계가 가능한 통합 프레임워크를 제공한다. 이는 차세대 고이동·고주파 무선 시스템에서 핵심 전송 기술로 자리매김할 잠재력을 가진다.

📄 논문 본문 발췌 (Translation)

무선 통신 응용이 전통적인 다중경로 환경에서 무인항공기와 같은 고이동 시나리오로 확장됨에 따라 다중화 기술도 이에 맞추어 발전하고 있다. 기존의 단일반송파 주파수 영역 등화(SC‑FDE)와 정교한 직교 주파수 분할 다중화(OFDM)는 Toeplitz 구조를 갖는 다중경로 채널 행렬을 이용하거나, 이중 선택성 채널을 활용하는 OTFS 및 AFDM과 같은 새로운 방식에 의해 대체되었다. 이러한 방법들은 채널을 대각화하거나 희소화함으로써 저복잡도 검출을 가능하게 한다. 그러나 이러한 구조에 대한 의존성은 실제 동적 환경에서의 견고성을 크게 제한한다.

본 논문은 물리적 채널과 무관하게 동작하는 무작위 다중화(Random Multiplexing) 기법을 연구한다. 무작위 변환 영역에서 등방성 입력 채널 행렬을 구성함으로써 전송 신호에 대한 통계적 페이딩 채널 에르고딕성을 달성한다. 또한, 임의의 노름 제한 및 스펙트럼 수렴 채널 행렬에 대해 고유 고정점 가정 하에 AMP‑계열 검출기의 복제 MAP 비트 오류율(BER) 최적성을 보장한다.

본 연구에서는 시간 영역 채널의 희소성과 등방성 입력을 동시에 활용하는 저복잡도 교차 영역 메모리 AMP(CD‑MAMP) 검출기를 고려한다. 복제 MAP BER을 최소화하고 복제 제약 용량을 최대화하기 위한 최적 전력 할당식을 도출하고, 최적 코딩 원칙 및 CD‑MAMP 검출기의 복제 제약 용량 최적성을 조사한다. 또한, 무작위 다중화가 다양한 무선 응용 분야에 적용될 수 있음을 탐색한다. 수치 결과를 통해 이론적 결과를 검증한다.

📄 ArXiv 원문 PDF 보기