숨은 수학 문제로 본 LLM 추론 능력 평가
📝 원문 정보
- Title: Evaluating the Reasoning Abilities of LLMs on Underrepresented Mathematics Competition Problems
- ArXiv ID: 2512.24505
- 발행일: 2025-12-30
- 저자: Samuel Golladay, Majid Bani-Yaghoub
📝 초록 (Abstract)
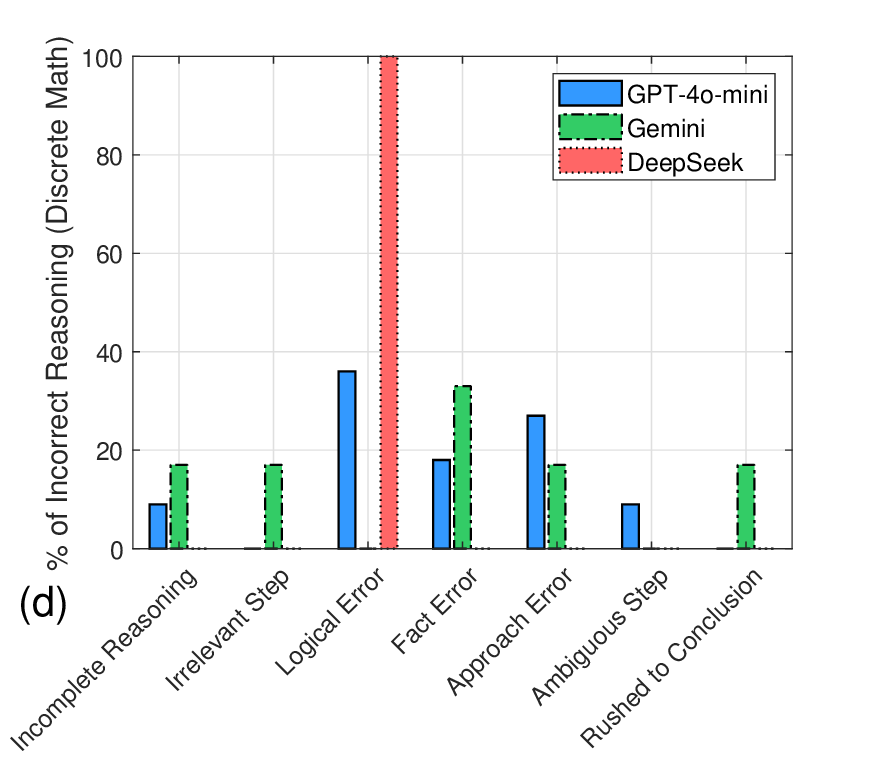
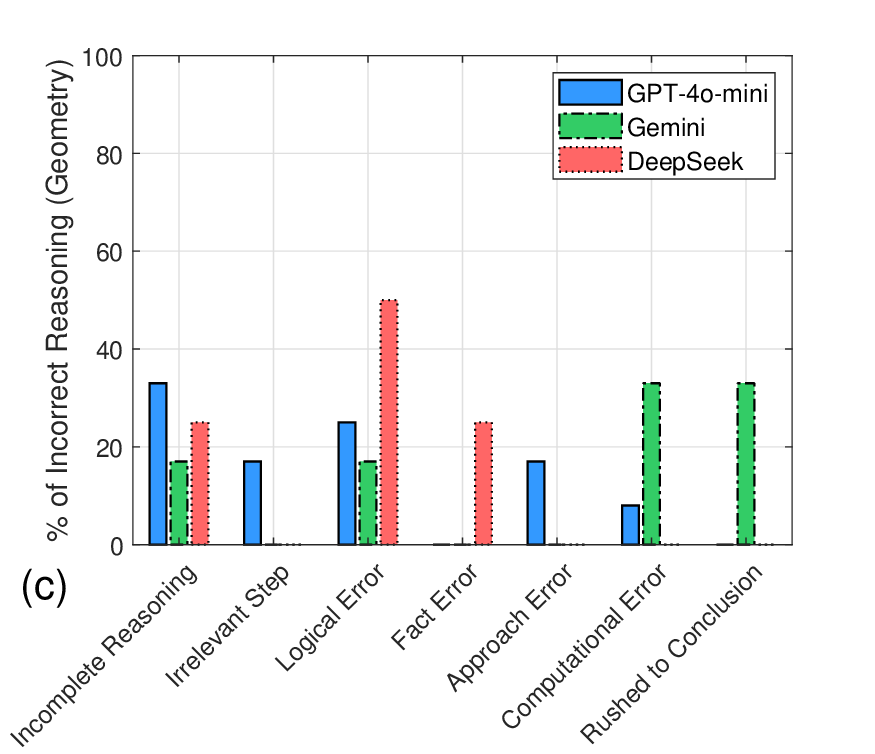
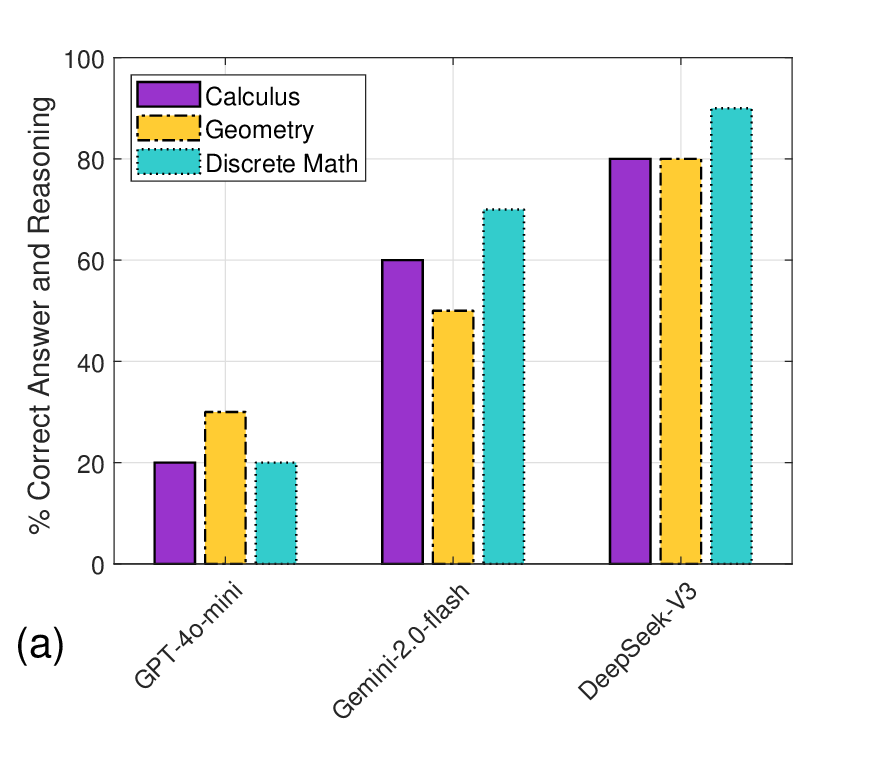
대형 언어 모델(LLM)의 수학적 추론 한계를 이해하려는 연구가 최근 활발히 진행되고 있으나, 대부분 동일한 벤치마크 데이터셋에 의존해 일반화 가능성이 제한되고 다양한 수학 과제의 도전을 충분히 포착하지 못한다는 비판이 있다. 본 연구는 이러한 한계를 보완하고자, 과소대표된 수학 경시 문제인 미주리 대학 수학 경시대회(Missouri Collegiate Mathematics Competition) 문제들을 활용해 세 가지 주요 분야(미적분, 해석기하, 이산수학)에서 LLM의 성능을 평가한다. GPT‑4o‑mini, Gemini‑2.0‑Flash, DeepSeek‑V3 세 모델에 동일한 프롬프트를 제공하고, 각 모델의 답안을 정답과 비교해 영역별 정확도를 산출하였다. 또한 모델별 추론 과정을 분석해 오류 유형과 패턴을 탐색하였다. 결과적으로 DeepSeek‑V3가 미적분(80%), 해석기하(80%), 이산수학(90%)에서 가장 높은 정확도를 기록했으며, 세 모델 모두 기하 영역에서 현저히 낮은 성능을 보였다. DeepSeek‑V3의 오류는 주로 계산 실수와 논리적 착오였고, GPT‑4o‑mini는 논리 전개와 접근 방식 선택에서 빈번히 실수를 범했다. Gemini‑2.0‑Flash는 추론 과정이 불완전하거나 성급한 결론에 도달하는 경향이 있었다. 결론적으로, 과소대표된 수학 경시 데이터셋을 활용한 평가가 LLM의 고유 오류 패턴을 드러내고, 특히 기하 분야에서 구조화된 추론 능력 향상의 필요성을 강조한다.💡 논문 핵심 해설 (Deep Analysis)
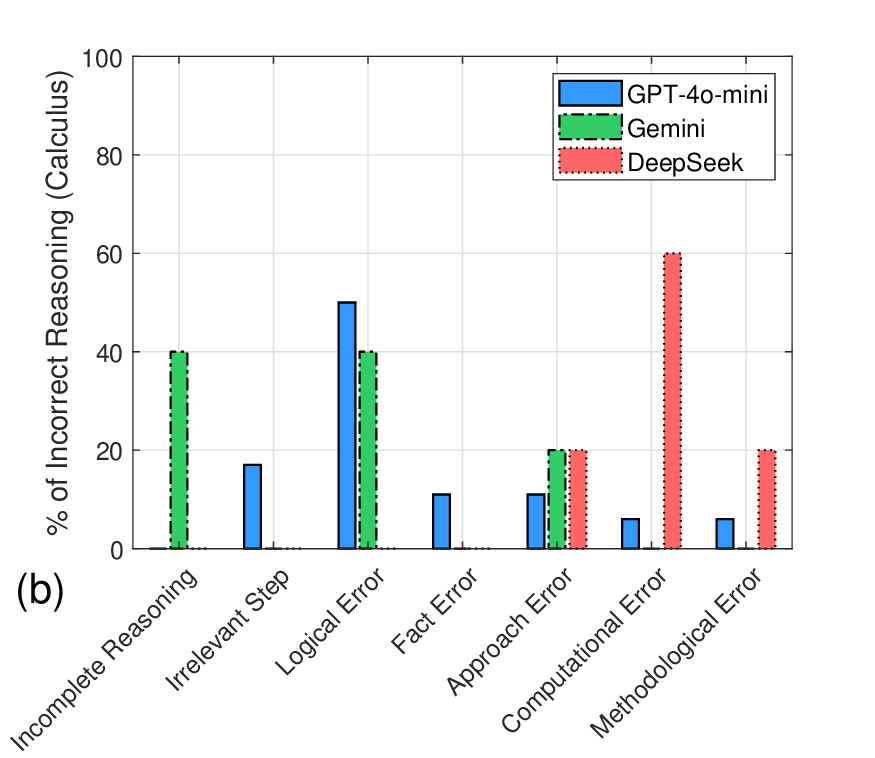
데이터 전처리 단계에서는 각 문제를 텍스트 형태로 변환하고, 정답과 상세 풀이 과정을 메타데이터로 첨부하였다. 프롬프트 설계는 “문제를 읽고, 풀이 과정을 단계별로 서술한 뒤 최종 답을 제시하라”는 일관된 지시문을 사용했으며, 모델마다 온도(temperature)와 최대 토큰 수를 동일하게 설정해 비교 조건을 통일하였다. 평가 지표는 (1) 최종 답의 정확도, (2) 풀이 과정에서 논리적 일관성 유지 여부, (3) 계산 단계에서 발생한 오류 유형으로 구분하였다.
결과 분석에서 DeepSeek‑V3는 전체 평균 83.3%의 정확도를 기록했으며, 특히 이산수학 영역에서 90%라는 높은 점수를 얻었다. 이는 그래프 이론, 조합론 등 논리적 구조가 명확한 문제에서 모델이 규칙 기반 추론을 잘 수행함을 시사한다. 반면, 미적분과 해석기하에서는 계산 단계에서 소수점 오차나 미분·적분 공식 적용 실수가 다소 눈에 띄었다. GPT‑4o‑mini는 전반적으로 논리 전개의 흐름이 부드럽지 못하고, 문제 접근 방법을 선택할 때 “어떤 공식을 써야 할지” 판단에 오류가 빈번했다. 이는 모델이 문제의 핵심을 파악하기보다 표면적인 키워드에 의존하는 경향을 보여준다. Gemini‑2.0‑Flash는 풀이 과정이 종종 중간에 끊기거나, 중간 단계에서 충분한 근거를 제시하지 않은 채 결론에 도달하는 경우가 있었다. 이는 모델이 “빠른 답변”을 우선시하면서 추론 깊이를 희생하는 현상으로 해석될 수 있다.
특히 모든 모델이 기하 영역에서 낮은 성능(30% 이하)을 보인 점은 주목할 만하다. 기하 문제는 시각적 사고와 다중 단계의 논리 전개가 요구되는데, 텍스트 기반 LLM은 이러한 공간적 관계를 내부적으로 재구성하는 데 한계가 있음을 암시한다. 향후 멀티모달 모델이나 외부 도구(예: 수학 엔진)와의 연동이 필요할 것으로 보인다.
연구의 한계로는(1) 샘플 수가 제한적이며, 특정 대회 문제에 편중된 점, (2) 프롬프트 설계가 단일 형태에 머물러 다양한 질문 방식에 대한 모델의 적응성을 평가하지 못한 점, (3) 인간 평가자의 주관적 판단이 포함된 추론 일관성 평가가 객관적 메트릭으로 완전히 대체되지 못한 점을 들 수 있다. 향후 연구에서는 더 다양한 국제 수학 경시 문제를 포함하고, 자동화된 논리 검증 도구와 결합해 추론 과정의 정밀성을 계량화하는 방안을 모색해야 한다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리