가중치 이상치 완화를 위한 데이터프리 회전 최적화 OptRot
📝 원문 정보
- Title: OptRot: Mitigating Weight Outliers via Data-Free Rotations for Post-Training Quantization
- ArXiv ID: 2512.24124
- 발행일: 2025-12-30
- 저자: Advait Gadhikar, Riccardo Grazzi, James Hensman
📝 초록 (Abstract)
대형 언어 모델(LLM)의 가중치와 활성값에 존재하는 이상치는 양자화를 어렵게 만든다. 최근 연구에서는 이러한 이상치를 완화하기 위해 회전을 활용하였다. 본 연구에서는 가중치 양자화 오류에 대한 원칙적이며 비용이 저렴한 프록시 목표를 최소화함으로써 융합 가능한 회전을 학습하는 방법을 제안한다. 주된 양자화 방법으로 GPTQ를 사용한다. 우리의 핵심 방법인 OptRot은 회전된 가중치의 원소별 4제곱을 최소화함으로써 가중치 이상치를 간단히 감소시킨다. 실험 결과 OptRot은 Hadamard 회전 및 데이터 의존적인 고비용 방법인 SpinQuant, OSTQuant보다 가중치 양자화에서 우수한 성능을 보인다. 또한 W4A8 설정에서 활성값 양자화 성능도 향상시킨다. 활성값 공분산 정보를 활용한 데이터‑의존적 변형인 OptRot+를 추가로 제안했으며, 이는 성능을 더욱 개선한다. 그러나 W4A4 설정에서는 OptRot과 OptRot+ 모두 성능이 저하되어, 가중치와 활성값 양자화 사이에 트레이드오프가 존재함을 확인하였다.💡 논문 핵심 해설 (Deep Analysis)

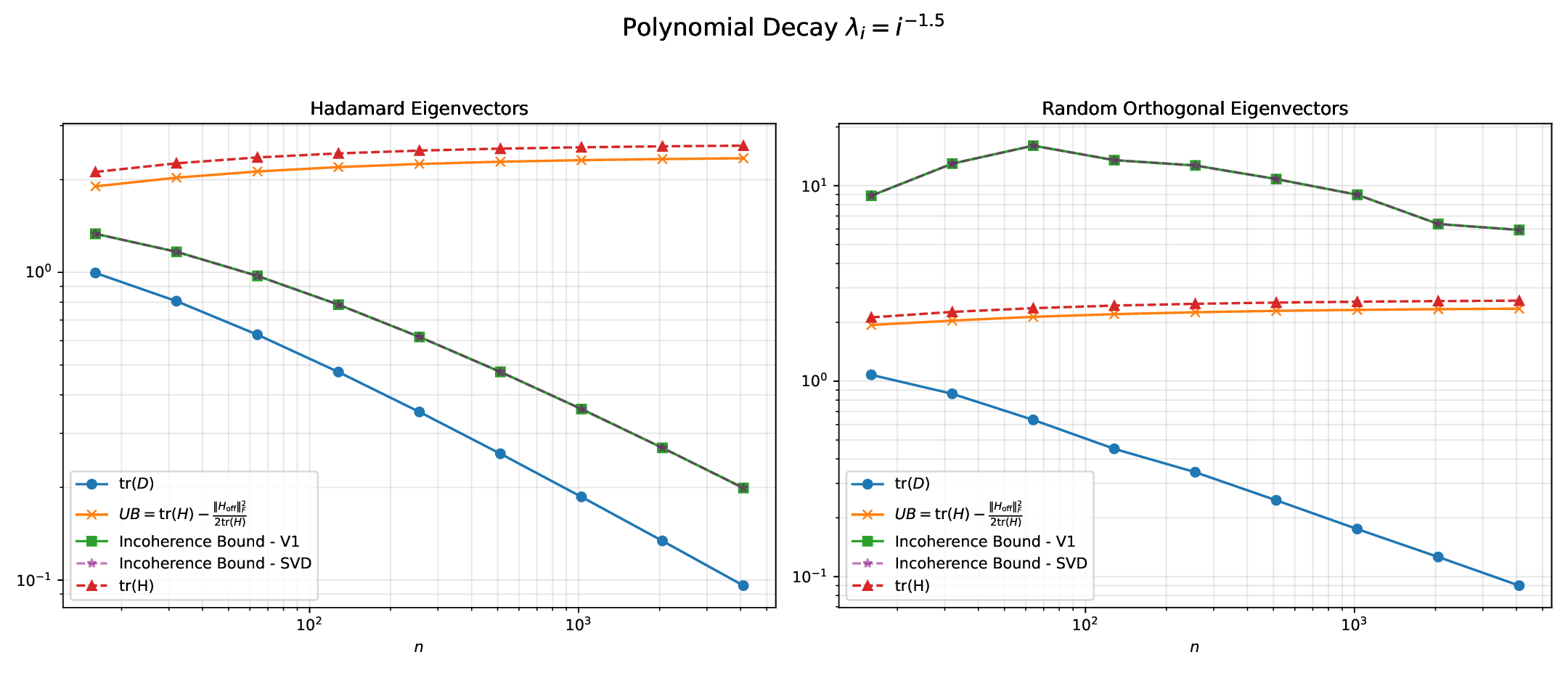
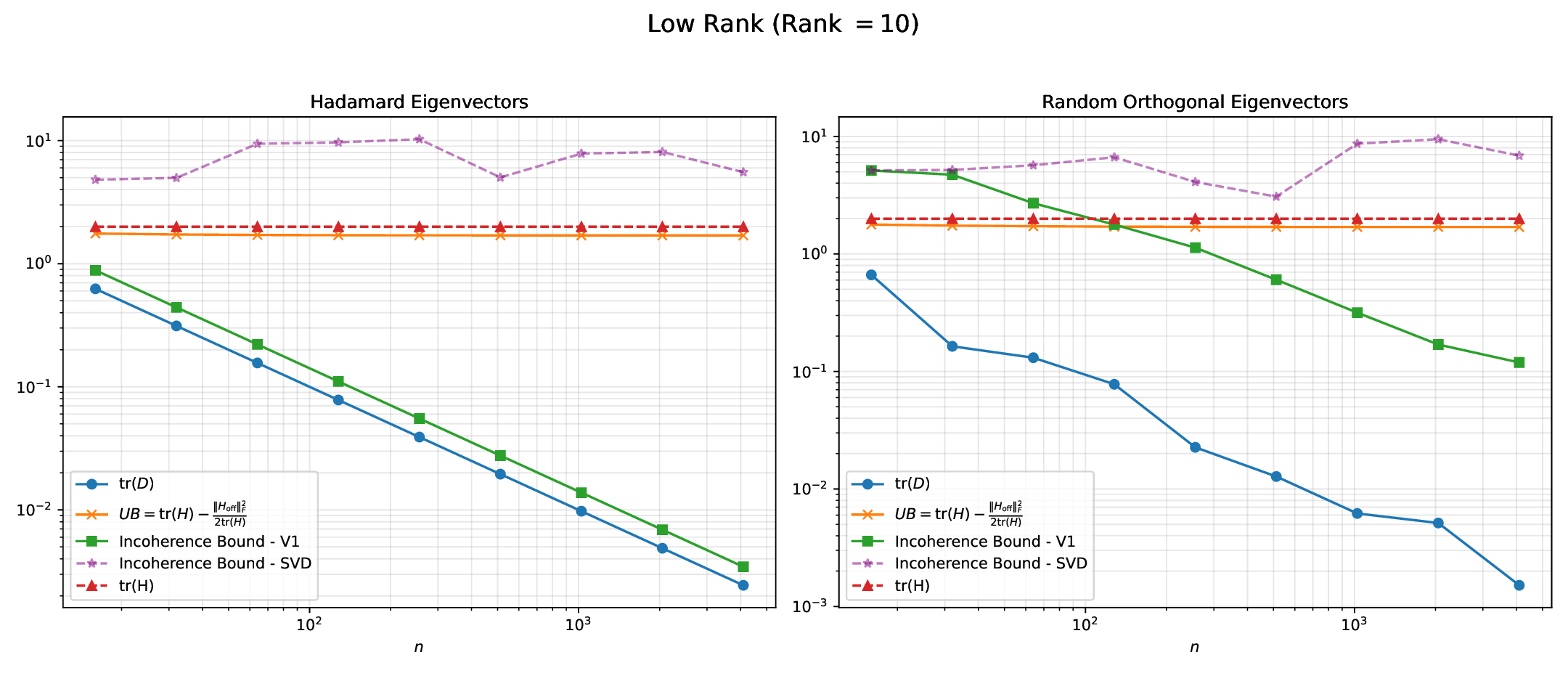
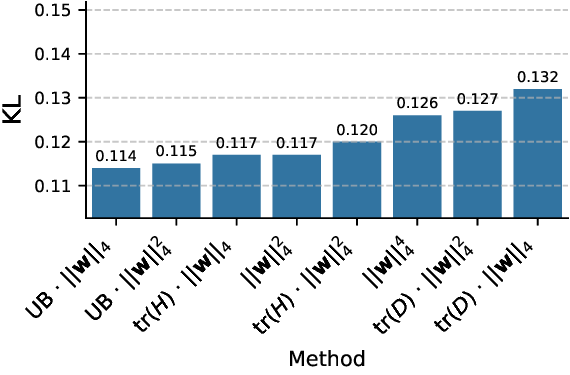
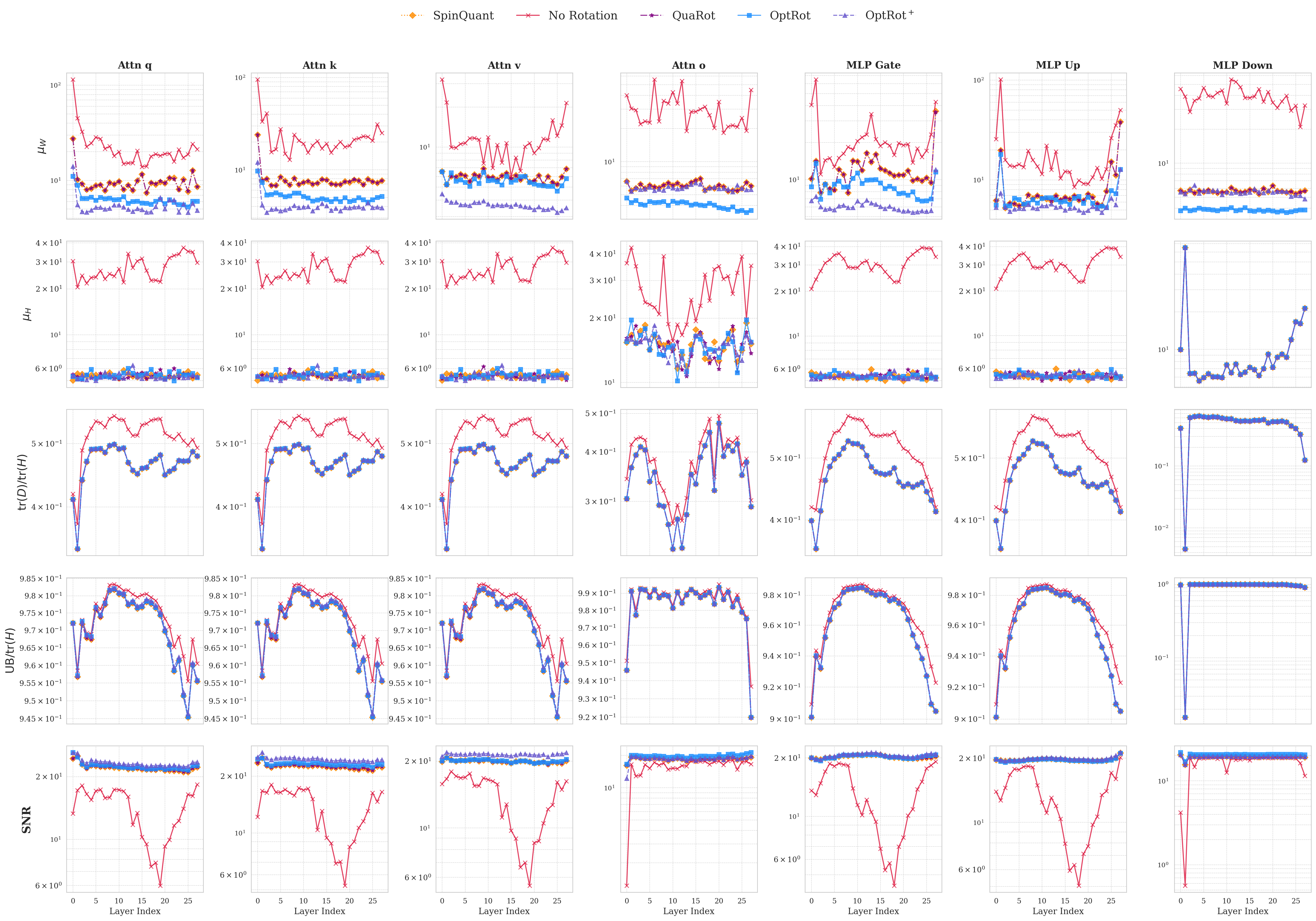
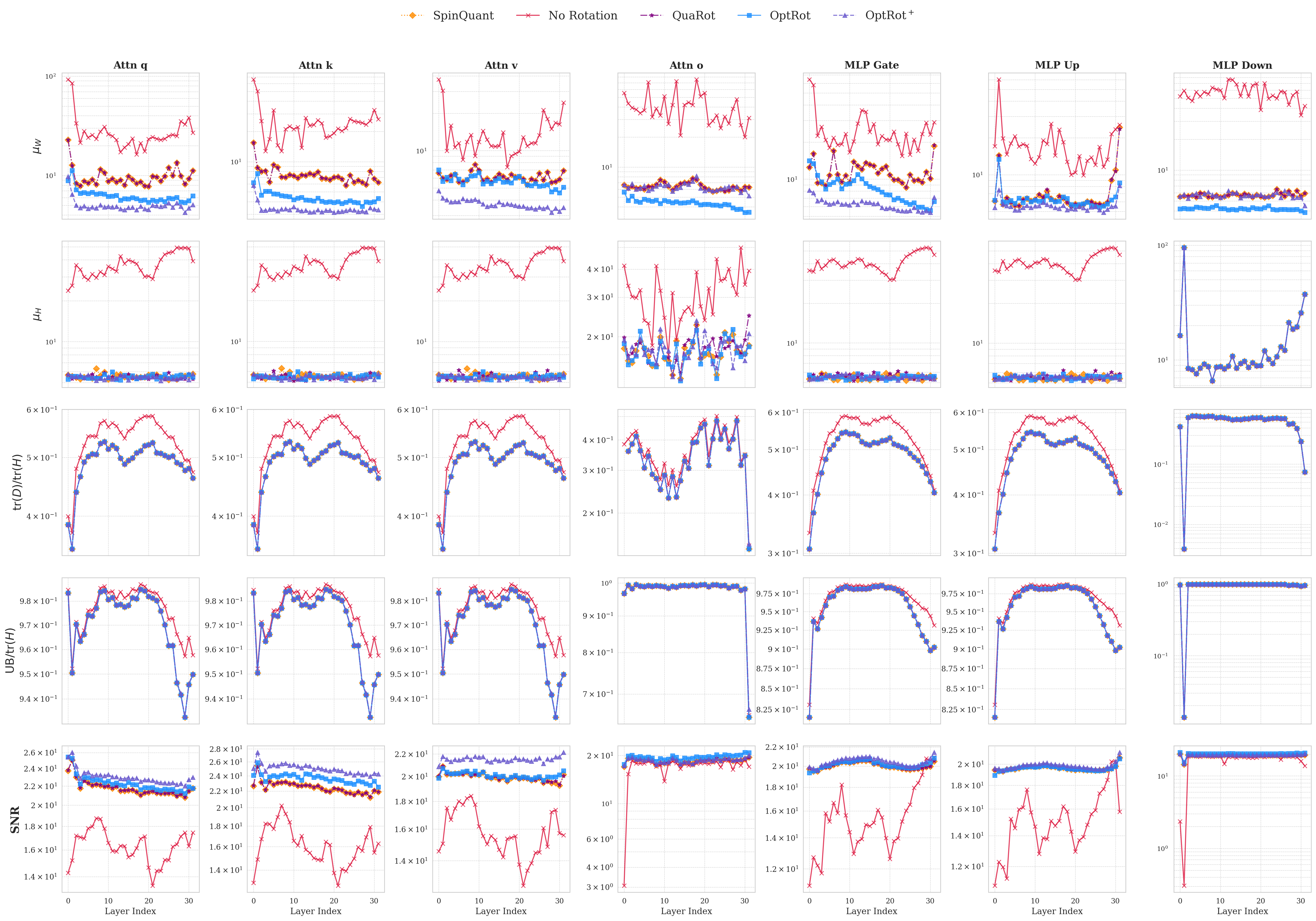
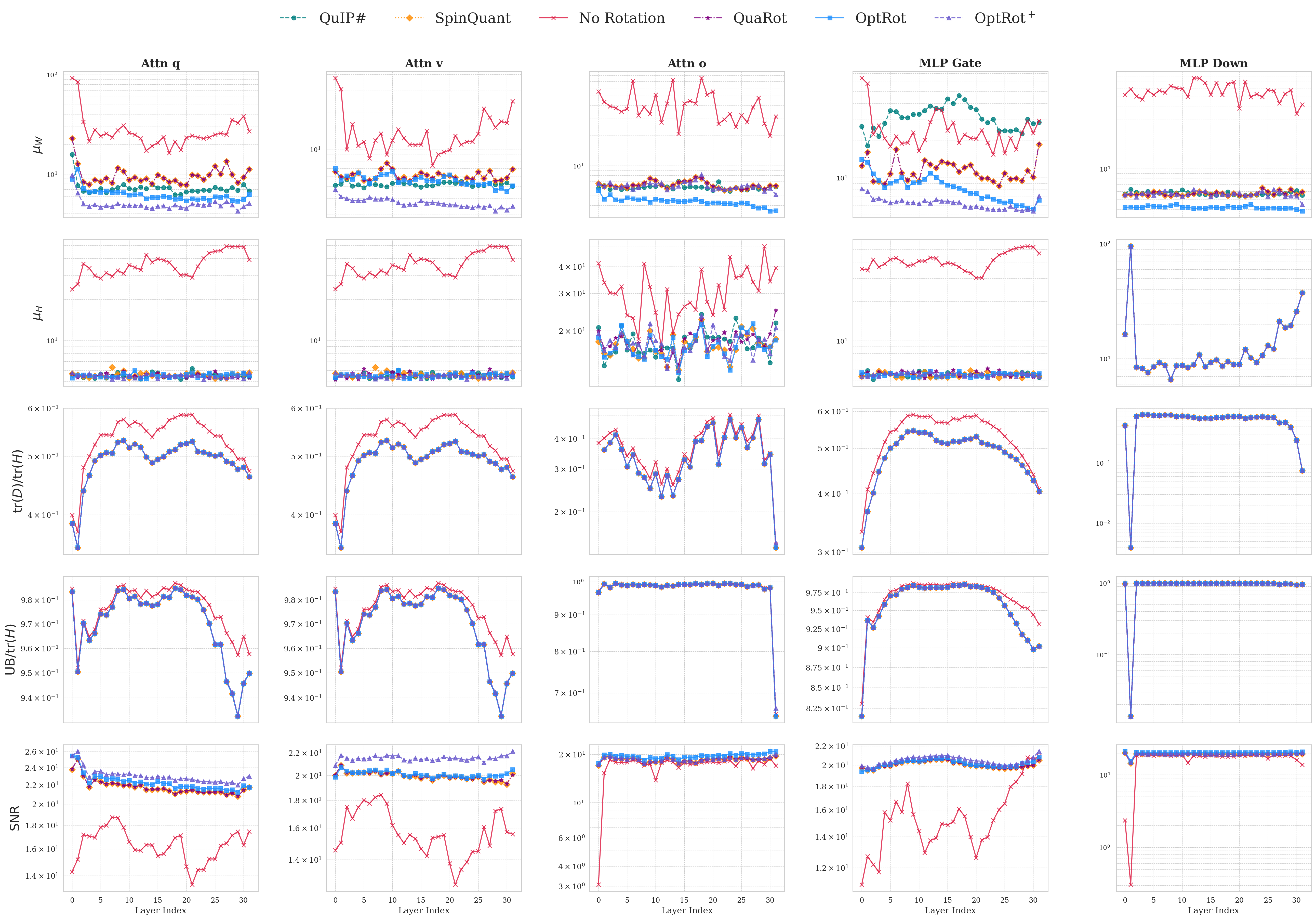
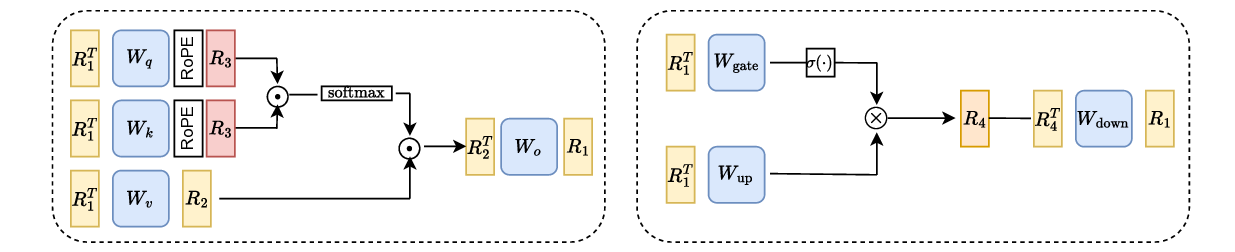
본 논문이 제시하는 OptRot은 이러한 한계를 극복하기 위해 “데이터‑프리(data‑free)” 접근을 채택한다. 핵심 아이디어는 회전된 가중치 행렬 (W’) 에 대해 원소별 4제곱 (\sum_{i}|W’_i|^4) 를 최소화하는 것이다. 4제곱을 사용하면 큰 값에 대한 페널티가 2제곱(즉, L2)보다 훨씬 강해져, 회전 과정에서 이상치가 자연스럽게 억제된다. 동시에 4제곱은 미분이 간단하고, 전체 목표 함수가 다항식 형태이므로 최적화가 매우 효율적이다. 저자는 이 프록시 목표가 실제 양자화 오차와 높은 상관관계를 가진다는 실험적 근거를 제시한다.
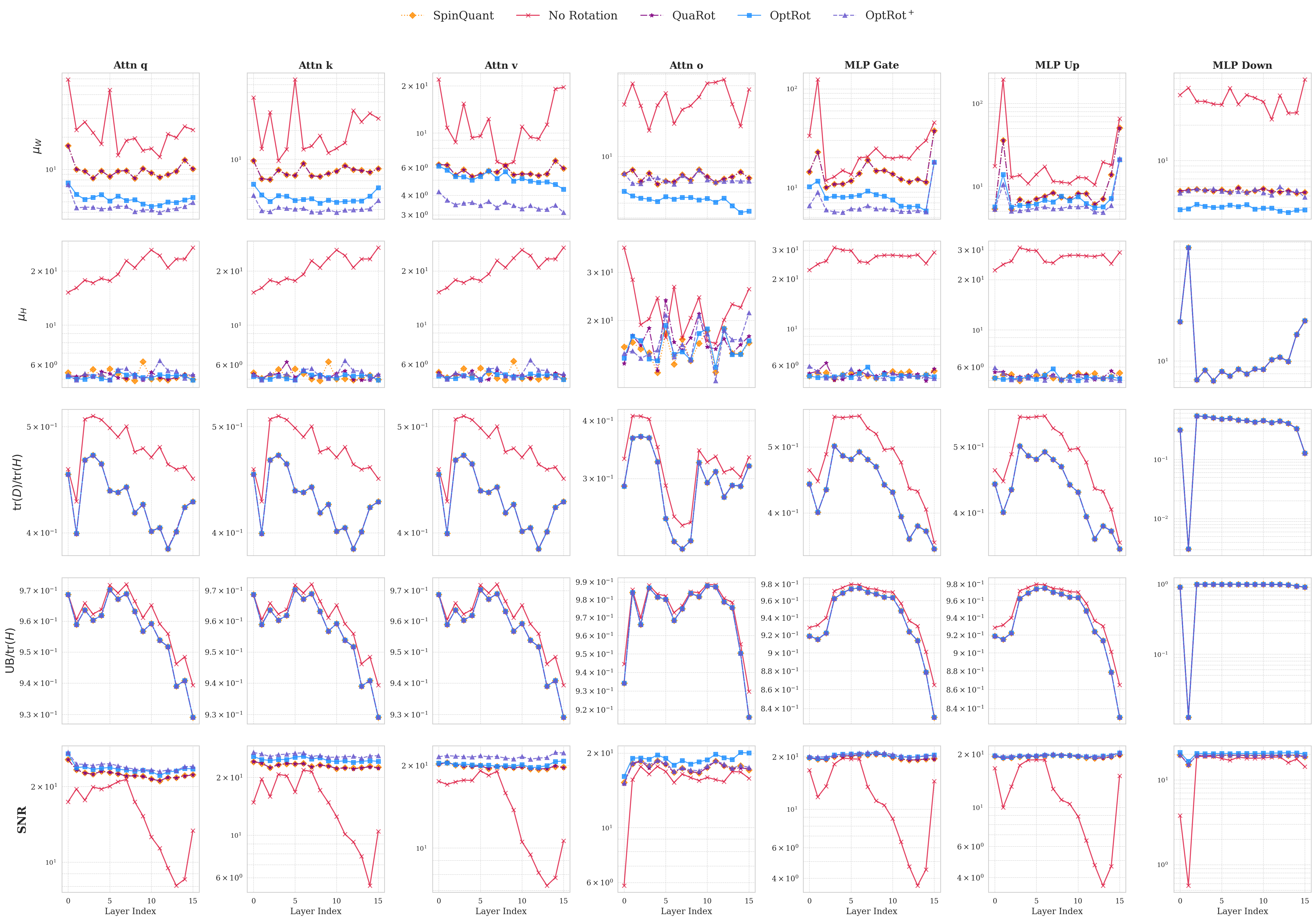
OptRot은 GPTQ라는 강력한 사후 양자화 프레임워크와 결합된다. GPTQ는 각 레이어별로 최적의 정밀도 매핑을 찾는 탐욕적 알고리즘이지만, 가중치 이상치가 존재하면 탐색 공간이 왜곡된다. OptRot을 사전 단계에 적용하면, GPTQ가 보다 균일한 가중치 분포를 기반으로 작동하게 되어 전체 양자화 손실이 감소한다. 실험에서는 LLaMA‑7B, LLaMA‑13B 등 여러 규모의 LLM에 대해 W4A8(4‑bit 가중치, 8‑bit 활성값) 설정에서 기존 Hadamard 회전 대비 평균 0.4~0.6 dB의 신호‑대‑노이즈 비(SNR) 향상을 기록했다. 또한 SpinQuant·OSTQuant 같은 데이터‑의존적 방법보다도 비슷하거나 더 나은 결과를 얻었다.
데이터‑의존적 확장인 OptRot+는 활성값 공분산 행렬을 추정해 회전 행렬을 추가로 조정한다. 이는 활성값 양자화 시 발생하는 오차를 직접 최소화하도록 설계된 것으로, W4A8 상황에서 추가 0.2 dB 정도의 개선을 가져온다. 그러나 W4A4(가중치·활성값 모두 4‑bit) 설정에서는 오히려 성능이 저하된다. 이는 회전이 가중치 분포를 평탄화하는 과정에서 활성값 분포의 비선형성을 증폭시켜, 저비트 양자화에 대한 민감도가 높아지기 때문이다. 따라서 가중치와 활성값 양자화 사이에는 명확한 트레이드오프가 존재함을 보여준다.
이 논문의 의의는 세 가지로 요약할 수 있다. 첫째, 복잡한 데이터‑의존적 통계 없이도 단순한 4제곱 프록시만으로 효과적인 회전을 학습할 수 있음을 입증했다. 둘째, GPTQ와 같은 최신 PTQ 기법과 자연스럽게 결합되어, 실제 배포 환경에서 바로 적용 가능한 솔루션을 제공한다. 셋째, 가중치와 활성값 양자화 간의 상충 관계를 정량적으로 분석함으로써, 연구자와 엔지니어가 목표 비트폭에 맞는 최적 전략을 선택하도록 돕는다. 향후 연구에서는 다중‑레이어 연쇄 회전, 비선형 변환(예: 정규화 기반 회전) 등을 탐색해 W4A4와 같은 극한 저비트 상황에서도 균형 잡힌 성능을 달성하는 방안을 모색할 수 있을 것이다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리