가족 모델 스케일링 법칙의 이론적 기반
📝 원문 정보
- Title: Theoretical Foundations of Scaling Law in Familial Models
- ArXiv ID: 2512.23407
- 발행일: 2025-12-29
- 저자: Huan Song, Qingfei Zhao, Ting Long, Shuyu Tian, Hongjun An, Jiawei Shao, Xuelong Li
📝 초록 (Abstract)
신경망 스케일링 법칙은 대규모 언어 모델(LLM) 학습 최적화의 핵심이지만, 일반적으로 단일 밀집 모델 출력을 전제로 한다. 이는 이기종 디바이스‑엣지‑클라우드 계층 전반에 걸친 보편적 지능 구현을 위한 “가족 모델(Familial Models)”이라는 변혁적 패러다임을 간과한다. 정적 아키텍처를 넘어, 가족 모델은 초기 종료와 릴레이 방식 추론을 결합해 하나의 공유 백본으로부터 G개의 배포 가능한 서브 모델을 생성한다. 본 연구는 이러한 “한 번 실행, 다수 모델” 패러다임을 포착하기 위해 모델 크기(N)와 학습 토큰(D) 외에 granularity(G)를 기본 스케일링 변수로 도입하고, 통합 함수형 L(N, D, G)를 제안한다. 대규모 실험을 통해 IsoFLOP 설계를 적용해 아키텍처 영향을 계산량으로부터 철저히 격리하였다. 고정 FLOP 예산(10¹⁹‑10²¹) 하에서 모델 크기와 granularity를 체계적으로 스위핑하고 토큰 수를 동적으로 조정하였다. 또한 개별 종료 수준의 거동을 밝히기 위해 branch scaling law를 도입했으며, 상위 브랜치가 성능에 미치는 영향은 무시할 수 있음을 확인했다. 이 법칙들을 기반으로 Efficiency Leverage(EL) 지표를 정의해 동일 FLOP 조건에서 가족 모델 평균 손실을 독립적인 동일 크기 밀집 모델과 비교하였다. 실험 결과 EL > 1이 모든 계산 구간과 granularity에서 관측되었으며, 특히 저계산량 영역에서 그 이점이 두드러졌다. 이론적으로는 고정‑계산 학습과 동적 아키텍처를 연결하고, 실용적으로는 “한 번 학습, 다수 배포” 패러다임이 밀집 모델의 계산 최적성을 손상시키지 않음을 입증한다.💡 논문 핵심 해설 (Deep Analysis)
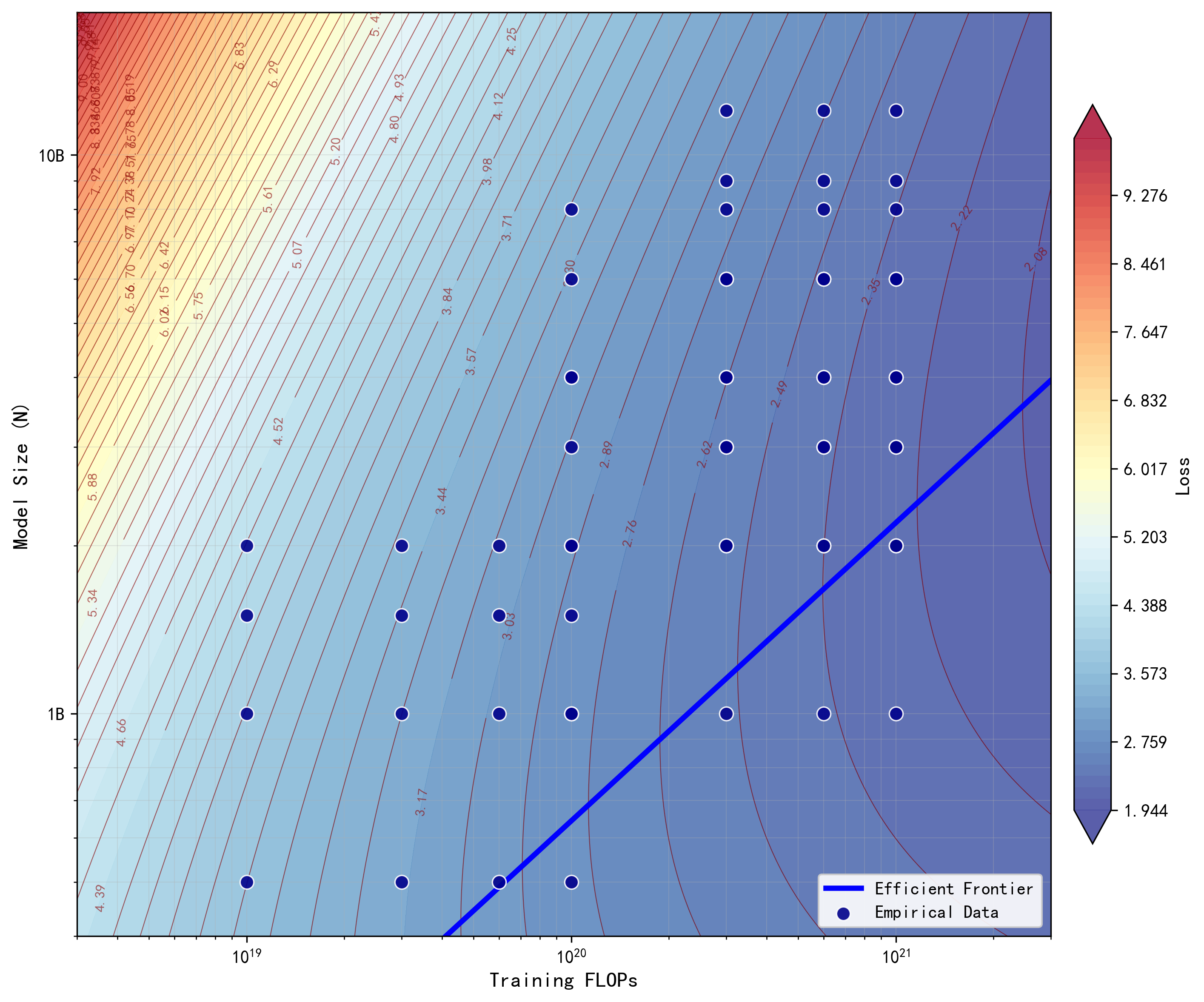
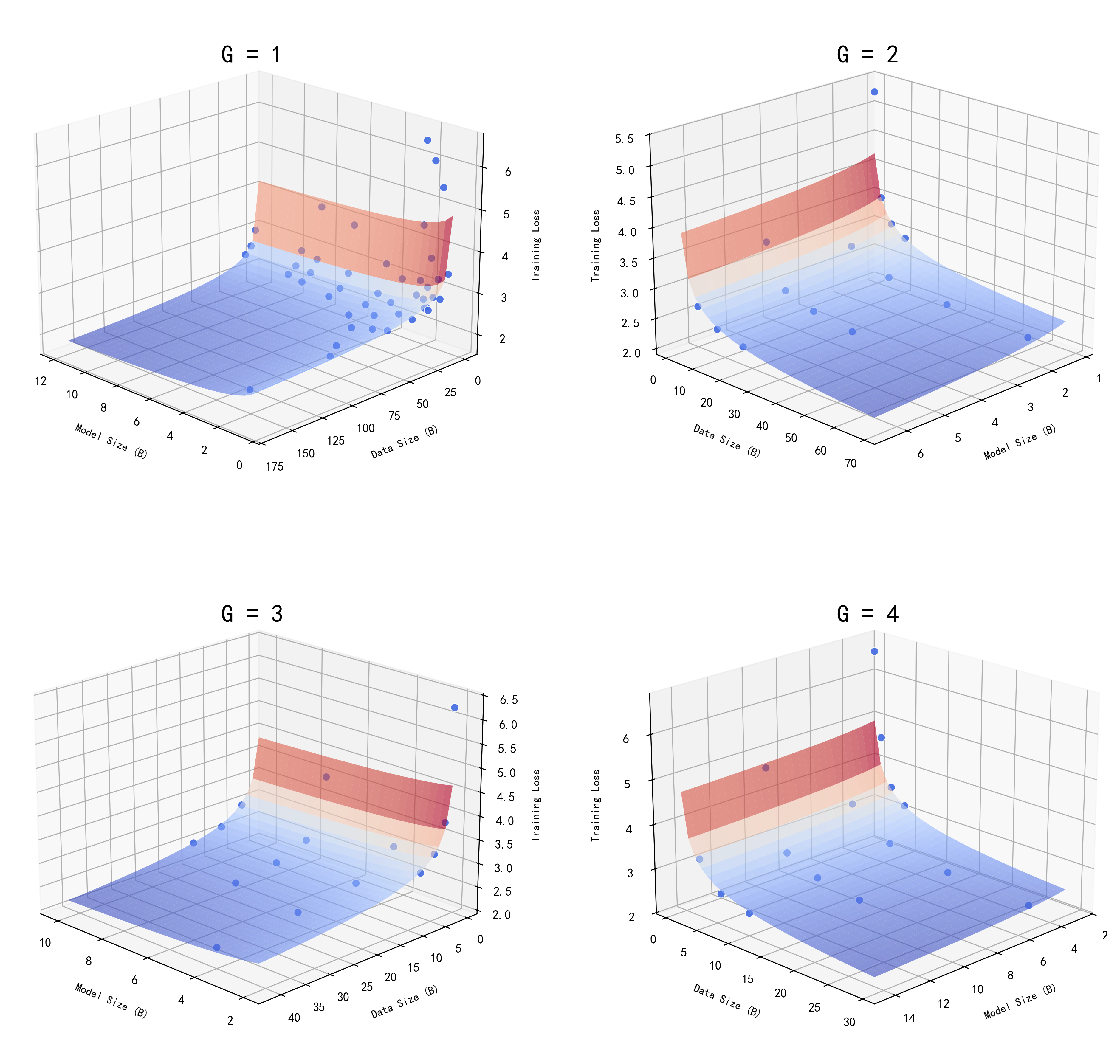
실험 설계는 특히 주목할 만하다. “IsoFLOP” 접근법을 통해 전체 FLOP 수를 일정하게 유지하면서 N과 G를 변동시키고, 그에 맞춰 D를 자동 조정한다. 이는 모델 크기와 granularity가 직접적으로 FLOP에 미치는 영향을 분리해 순수한 스케일링 효과만을 관찰할 수 있게 한다. 10¹⁹에서 10²¹ FLOP 범위는 현재 최첨단 LLM 훈련 규모와 일치하므로, 결과의 실용적 의미가 크다.
또한 “branch scaling law”를 도입해 개별 종료점(브랜치)의 영향을 별도로 분석한다. 실험 결과, 상위 브랜치(즉, 더 큰 서브 모델)들이 추가되더라도 전체 손실에 미치는 기여는 거의 무시할 수 있을 정도로 작았다. 이는 조기 종료가 모델 전체 성능을 크게 해치지 않으며, 오히려 계산 효율성을 크게 높일 수 있음을 시사한다.
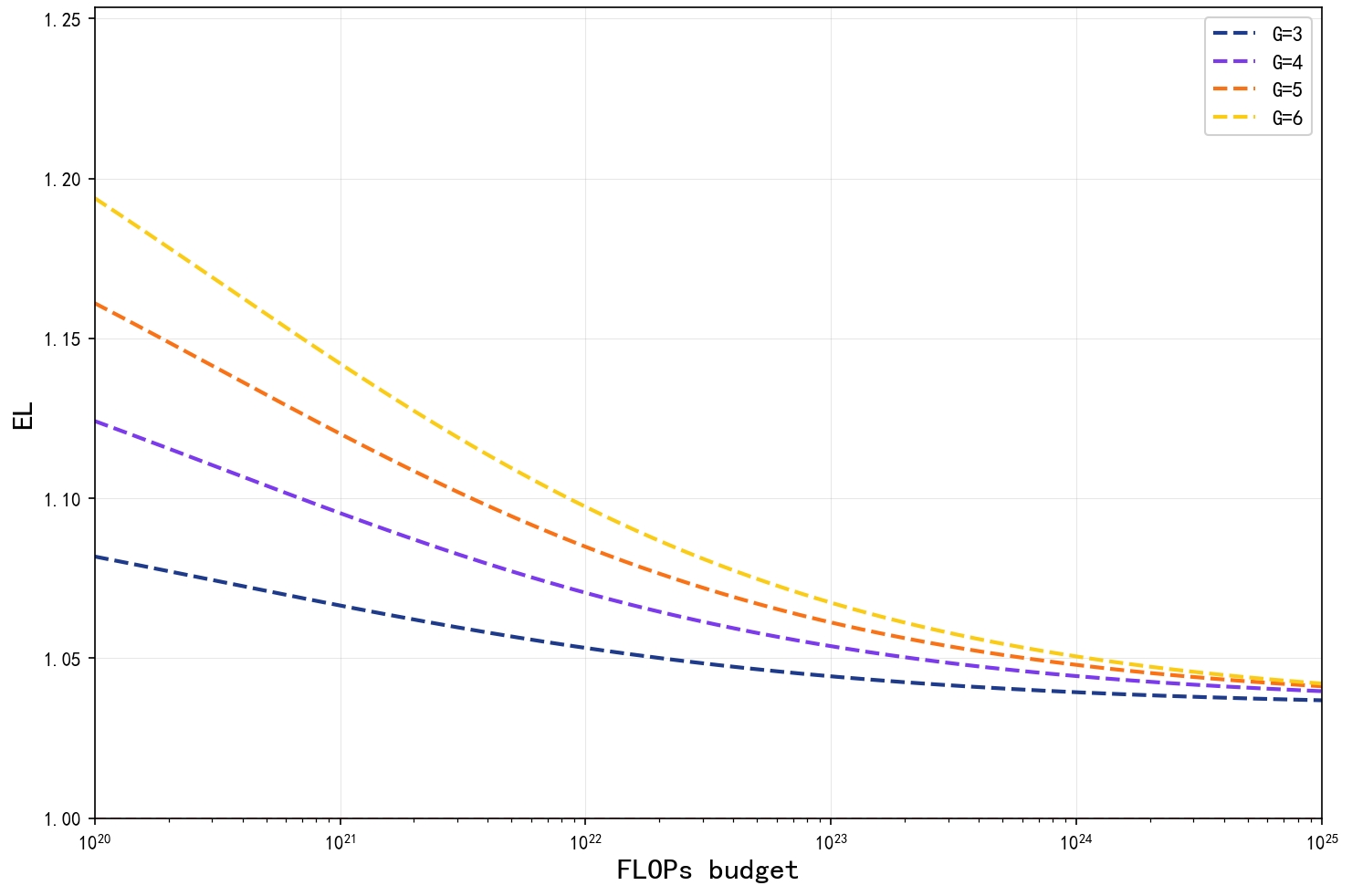
효율성 비교를 위해 제시된 Efficiency Leverage(EL) 지표는 동일 FLOP 조건에서 가족 모델과 독립적인 밀집 모델의 평균 손실 비율을 나타낸다. EL > 1이라는 결과는 같은 계산량을 사용했을 때 가족 모델이 손실 면에서 우수함을 의미한다. 특히 저계산량 구간에서 EL이 크게 나타나는 것은, 제한된 자원 환경(예: 모바일 디바이스, 엣지 서버)에서 가족 모델이 더욱 큰 이점을 제공한다는 실용적 메시지를 담고 있다.
이론적 관점에서 보면, N‑D‑G 3차원 스케일링 법칙은 기존 2차원 법칙을 일반화한 형태이며, 고정‑계산 훈련과 동적 아키텍처(조기 종료, 릴레이 추론) 사이의 연결 고리를 제공한다. 이는 “한 번 학습, 다수 배포”라는 전략이 단순한 엔지니어링 트릭이 아니라, 수학적으로도 최적화된 선택임을 뒷받침한다. 앞으로는 G 외에도 하드웨어 특성(전력, 메모리 대역폭) 등을 추가 변수로 확장하거나, 다중 태스크 전이 학습과 결합해 보다 포괄적인 스케일링 프레임워크를 구축할 여지가 있다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리