자기반성을 통한 내재적 선호 최적화 InSPO
📝 원문 정보
- Title: InSPO: Unlocking Intrinsic Self-Reflection for LLM Preference Optimization
- ArXiv ID: 2512.23126
- 발행일: 2025-12-29
- 저자: Yu Li, Tian Lan, Zhengling Qi
📝 초록 (Abstract)
직접 선호 최적화(DPO)와 그 변형은 단순성과 오프라인 안정성 때문에 대형 언어 모델(LLM) 정렬의 표준으로 자리 잡았다. 그러나 현재 방법에는 두 가지 근본적인 한계가 있다. 첫째, 현재 방법으로 도출된 정책은 불변성을 결여한다. 스칼라화 함수(예: Bradley‑Terry 모델의 로지스틱 함수)나 기준 정책과 같은 모델링 선택에 따라 정책이 달라지며, 이는 인간 선호를 반영하기보다 파라미터화의 부작용으로 나타난다. 최적 정책은 이러한 불변성을 만족해야 한다. 둘째, 기존 방법이 도출한 정책은 이론적으로 최적이 아니다. 쌍별 선호 데이터에 내재된 비교 정보를 충분히 활용하지 못해 “비교와 대조” 능력이 제한된다. 이를 해결하기 위해 우리는 내재적 자기반영 선호 최적화(InSPO)라는 새로운 방법군을 제안한다. InSPO는 쌍별 선호 설정에서 대안 응답을 조건으로 하는 전역 최적 정책을 유도하여 자기반영 개념을 명시적으로 형식화한다. 이론적으로 InSPO는 표준 DPO와 RLHF 목표보다 우수하고 스칼라화 함수와 기준 정책 선택에 대한 불변성을 보장한다. 실용적으로 InSPO는 DPO 계열 알고리즘에 플러그인 형태로 적용 가능하며, 복잡한 아키텍처 변경 없이 정렬 목표를 모델링 제약으로부터 분리한다. 특권 정보 학습(learning using privileged information) 개념을 활용해 배포 시 대안 응답을 생성할 필요가 없으므로 추론 비용이 추가되지 않는다. 다양한 DPO 계열 알고리즘에 적용한 실험 결과, InSPO가 승률과 길이 제어 지표에서 일관된 향상을 보이며, 자기반영 메커니즘이 보다 견고하고 인간에 맞는 LLM을 만든다는 것을 입증한다.💡 논문 핵심 해설 (Deep Analysis)
두 번째 결함은 ‘정보 활용의 비효율성’이다. 기존 DPO는 쌍별 선호 데이터에서 “A가 B보다 좋다”는 비교만을 이용해 정책을 학습한다. 하지만 이러한 비교는 사실상 두 응답 사이의 상대적 정보를 모두 포함하고 있다. 예를 들어, A가 B보다 더 구체적이고, B가 A보다 더 간결하다는 세부적인 차이를 내포한다. 현재 방법은 이러한 미세한 차이를 충분히 활용하지 못하고, 단순히 승패 신호만을 반영한다. 결과적으로 모델은 ‘비교와 대조’를 통한 자기반성(self‑reflection) 능력이 제한되어, 복잡한 질문에 대해 보다 깊이 있는 답변을 생성하는 데 한계가 있다.
InSPO는 이러한 두 문제를 동시에 해결한다. 이론적으로, 저자들은 쌍별 선호 데이터를 ‘조건부 정책’ 형태로 재구성한다. 즉, 정책 πθ는 단순히 컨텍스트 c만이 아니라, 대안 응답 a′(즉, 비교 대상)도 입력으로 받아서 “c와 a′를 고려했을 때 어떤 응답 a가 더 선호되는가”를 직접 모델링한다. 이렇게 하면 정책은 자연스럽게 ‘자기반영’ 메커니즘을 내재하게 된다. 중요한 점은 이 정책이 전역 최적임을 증명했으며, 스칼라화 함수와 기준 정책에 대한 의존성이 사라져 불변성을 만족한다는 것이다.
실제 구현 측면에서 InSPO는 ‘특권 정보 학습(learning using privileged information)’ 아이디어를 차용한다. 훈련 단계에서는 대안 응답 a′를 제공받아 자기반영 정책을 학습하지만, 배포 단계에서는 a′가 필요 없다. 학습된 정책은 이미 a′에 대한 정보를 내재화했기 때문에, 추론 시 추가적인 응답 생성 없이도 동일한 성능을 발휘한다. 따라서 기존 DPO‑family 알고리즘에 플러그인 형태로 쉽게 적용할 수 있으며, 모델 아키텍처를 크게 바꾸지 않아도 된다.
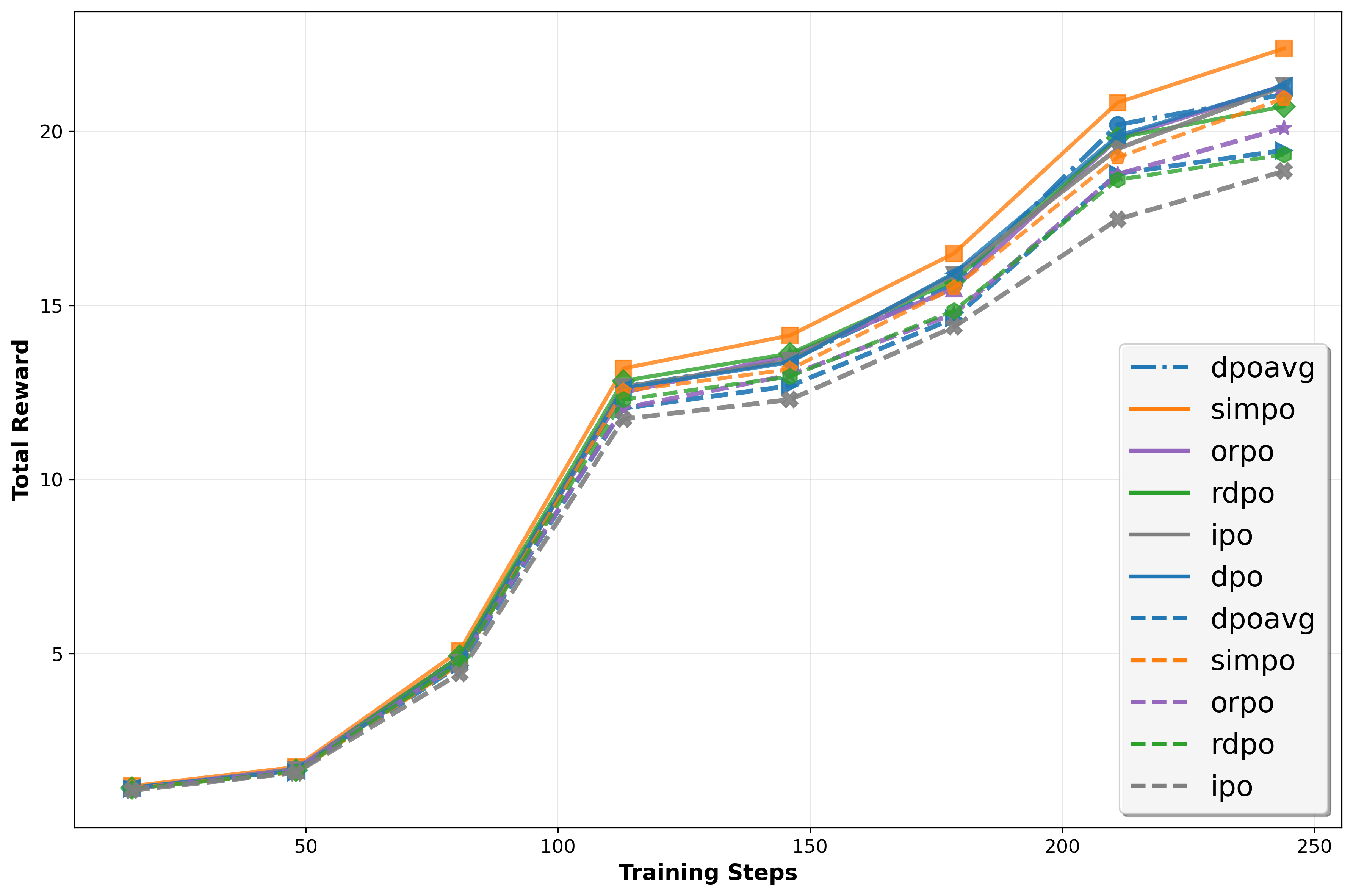
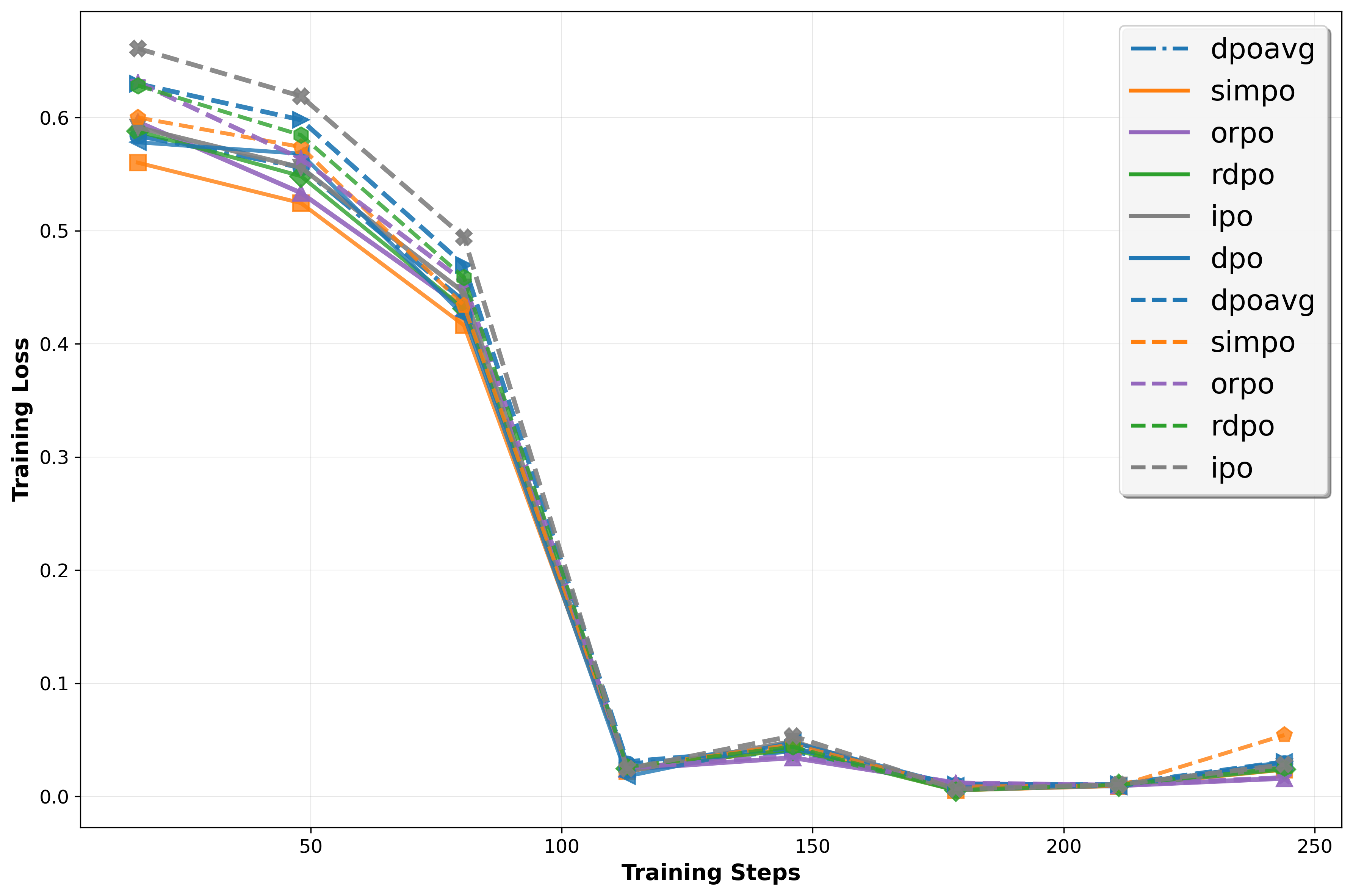
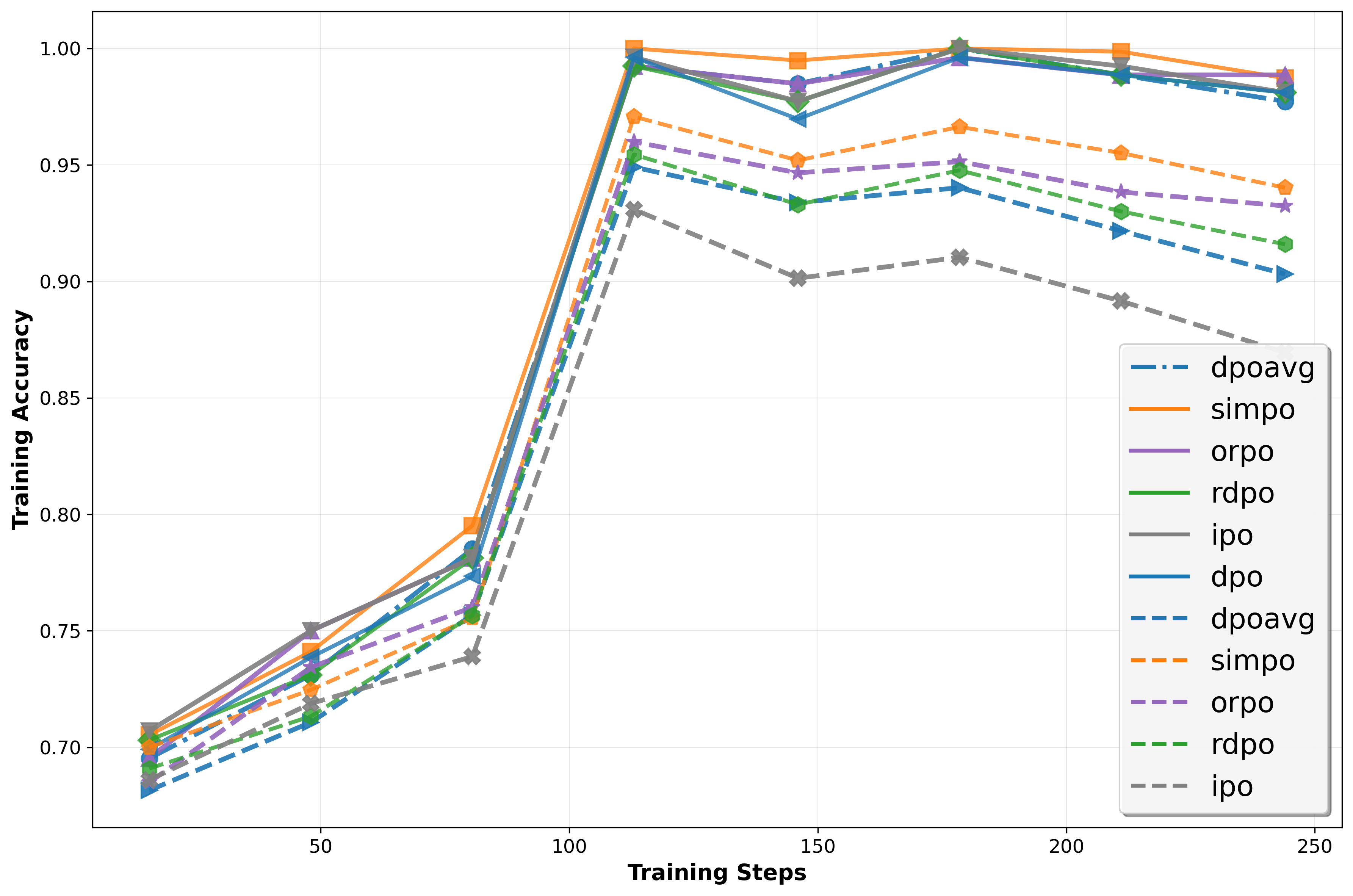
실험 결과는 설득력 있다. 다양한 규모와 아키텍처의 LLM에 InSPO를 적용했을 때, 승률(win rate)과 길이‑제어(length‑controlled) 메트릭 모두에서 일관된 상승을 보였다. 특히, 인간 평가자와의 직접적인 비교 실험에서 InSPO 모델이 기존 DPO 모델보다 더 자연스럽고, 질문 의도에 부합하는 답변을 제공한다는 점이 강조된다. 이는 ‘자기반영’이라는 메커니즘이 모델의 응답 품질을 실질적으로 향상시킨다는 강력한 증거다.
요약하면, InSPO는 DPO의 두 핵심 약점을 이론적·실용적으로 보완한 프레임워크이며, 불변성을 보장하면서도 비교 정보를 최대한 활용하는 새로운 정책 학습 방식을 제시한다. 이러한 접근은 향후 LLM 정렬 연구에서 ‘자기반영’이라는 개념을 중심으로 한 새로운 패러다임을 열어줄 가능성이 크다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리