- 저자: Matthieu Destrade, Oumayma Bounou, Quentin Le Lidec, Jean Ponce, Yann LeCun
(본 연구에서는 JEPA 세계 모델의 계획 능력을 향상시키기 위해, 임시 Q 학습(IQL) 손실을 사용하여 상태 인코더를 학습함으로써 구조화된 표현 공간을 생성했습니다. 이 접근법은 기존 예측 기반 방법보다 더 정확한 계획 결과를 제공합니다.)
1. **기본적인 개념**: JEPA 세계 모델의 계획 능력을 향상시키는 데 초점을 맞춤.
- 비유: 이 연구는 자동차의 내비게이션 시스템을 업그레이드하는 것과 같음. 더 정확한 경로를 찾기 위해 새로운 지도 데이터를 추가함.
maketitle 감사 aketitle
서론
세계 모델은 시스템의 동적을 포착하도록 설계된 딥 러닝 아키텍처입니다. 이들은 주어진 액션 시퀀스에 대한 환경의 미래 상태를 예측하는 데 훈련됩니다. 시스템의 동적으로 명시적으로 모델링함으로써, 이들은 행동이 미래 결과에 미치는 인과적인 이해를 포착하여 가능한 궤적에 대해 추론하고 계획할 수 있습니다.
제안된 다양한 아키텍처 중에서 Joint-Embedded Predictive Architectures (JEPA)는 예측 표현을 학습하는 효과적인 프레임워크를 제공합니다. JEPA 모델은 자체 감독 예측 손실을 최적화함으로써 상태와 액션에 대한 표현을 함께 학습하고, 과거 상태와 행동을 미래 표현으로 매핑할 수 있는 예측자를 학습합니다. 이러한 형식은 표현 학습과 행동 계획 모두에서 효과적이었습니다.
이 연구에서는 JEPA 모델의 계획 능력을 향상시키는 것을 목표로 합니다. 강화 학습의 진전을 바탕으로, 임베디드 상태 간 유클리드 거리(또는 준거)가 도달 비용과 관련된 음의 목표 조건 가치 함수를 근사하도록 표현을 학습합니다. 이 구조는 계획을 위한 의미 있는 잠재 공간을 제공하며, 계획 최적화 중에 국소 최소값 문제를 완화할 수 있습니다. 우리는 제어 작업에서 우리의 방법을 평가하고, 이러한 표현을 포함한 모델이 표준 JEPA 모델보다 계획 성능이 일관되게 향상된다는 것을 관찰합니다.
관련 연구
JEPA 세계 모델
JEPA(Joint-Embedded Predictive Architectures)는 표현 학습과 행동 계획을 위한 세계 모델 구현에 효과적인 방법을 제공합니다. 이들은 미래 상태 예측이 원래 관찰 공간보다 학습된 표현 공간에서 더 쉽다는 가설에 기반하고 있으며, 예측 가능성을 강제하면 의미 있는 표현이 유도된다는 가정을 합니다. JEPA 모델은 일반적으로 상태 인코더, 액션 인코더 및 예측자로 구성됩니다. 이들은 상태와 행동의 시퀀스를 사용하여 예측 손실 $\mathcal{L}_\text{pred}$을 최소화하도록 훈련됩니다. 훈련 중에 붕괴를 방지하기 위해 표준 접근법은 VCReg 손실 $\mathcal{L}_\text{VCReg}$ 또는 지수 이동 평균(EMA) 스키마를 사용합니다.
최근 연구에서는 JEPA 모델을 행동 계획 작업에 적용하여 유망한 성능을 보였지만 여전히 한계가 있음을 보여주었습니다. 이를 위해, 그들은 최적화된 예측 제어(MPC) 절차를 사용하며, 이는 목표 표현과 예측된 표현 사이의 거리를 최소화하는 계획 손실을 반복적으로 최소화합니다.
가치 함수 학습
MPC의 효율성을 향상시키기 위해 여러 연구에서는 MPC 절차를 안내하기 위한 가치 함수 학습을 제안했습니다. 이 접근법은 MPC가 더 긴 시간 범위를 고려할 수 있도록 하고, 목표 도달 작업을 용이하게 하는 추가 비용 항을 제공함으로써 절차의 안정성을 높입니다.
암시적 Q 학습(IQL)은 기대값 회귀를 활용하여 무라벨 트래JECT로리에서 목표 조건 가치 함수를 학습합니다. 저자들은 IQL을 통해 시스템 상태의 구조화된 표현 공간을 학습하고, 그 공간에서 음의 유클리드 거리가 도달 비용에 해당하는 목표 조건 가치 함수를 근사하도록 합니다. 이 표현은 다양한 강화 학습 작업을 효과적으로 해결할 수 있음을 보여줍니다. 일반적으로 목표 조건 가치 함수는 대칭적이지 않기 때문에, 준거를 사용하여 이를 학습하는 방법이 제안되었습니다.
가치 지향 JEPA 행동 계획
JEPA 모델의 계획 능력을 향상시키기 위해, 우리는 MPC 계획 비용을 계산하는 데 사용되는 표현을 강화합니다. 표준 JEPA 프레임워크에서 계획은 예측된 상태와 목표 사이의 거리를 최소화하여 수행됩니다. 그러나 이 비용은 여러 국소 최소값을 가질 수 있어 최적화가 어렵습니다. 이를 해결하기 위해, 우리는 표현 공간에서 유클리드 거리가 주어진 환경에서 도달 비용과 관련된 음의 목표 조건 가치 함수를 근사하도록 학습합니다.
베이스라인 손실 함수
표현 공간에서 가치 함수 기준을 강제하기 위해, JEPA 모델의 상태 인코더에 대한 몇 가지 간단한 손실 함수를 고려하며 이들을 베이스라인으로 사용합니다. 구체적으로, 연속적인 상태를 양적 예로, 무작위 상태 쌍을 음성 예로 사용하여 대비 손실 $\mathcal{L}_\text{contrastive}$ 및 연속 상태 사이의 거리를 1로 강제하는 회귀 손실 $\mathcal{L}_\text{regressive}$를 적용합니다.
JEPA 모델을 위한 IQL
$`\mathcal{S}_0`$는 상태 공간, $`\theta`$는 매개변수이고 $`\mathcal{E}_\theta`$는 JEPA 모델의 상태 인코더입니다. 모든 $`(s, g) \in \mathcal{S}_0^2`$, 우리는 $`V_\theta(s, g) = -\Vert \mathcal{E}_\theta(s) - \mathcal{E}_\theta(g) \Vert_2`$을 정의합니다. 우리의 목표는 $`V_\theta`$가 도달 비용 $`C: (s, a, g) \mapsto \mathbf{1}_{s \neq g}`$와 관련된 목표 조건 가치 함수 $`V^\star`$를 근사하도록 $`\theta`$를 학습하는 것입니다. 이는 상태 $`s`$가 목표 $`g`$와 같지 않은 모든 시간 단계에서 패널티를 부과합니다.
$(T, N) \in \mathbb{N}^2$는 훈련 트래JECT로리의 길이와 훈련 목표의 수를 나타냅니다. $`\mathcal{D}`$는 트래JECT로리 $(s_t)_{t\in\llbracket0,T\rrbracket}$가 $\mathcal{S}_0^{T+1}$에 속하고, 목표 $(g_n)_{n\in\llbracket0,N\rrbracket}$가 $\mathcal{S}_0^{N+1}$에 속하는 데이터셋입니다. 우리는 $`\theta`$에 대해 평균 IQL 손실을 경사하강법으로 최소화합니다:
\begin{equation}
\forall ((s_t),(g_n)) \in \mathcal{D}, \quad
\mathcal{L}_\text{VF}^\theta((s_t),(g_n)) = \sum_{n=0}^N \sum_{t=0}^{T-1}
L_\tau^2 \Big( -\mathbf{1}_{s_t \neq g_n} + \gamma V_{\bar{\theta}}(s_{t+1}, g_n) - V_\theta(s_t, g_n) \Big),
\end{equation}
여기서 $`\bar{\cdot}`$는 stop-gradient를 나타내며; $`\tau, \gamma \in ]0,1[`$는 1에 가깝고 모든 $`x \in \mathbb{R},`$에 대해 $`\; L_\tau^2(x) = |\tau - \mathbf{1}_{x<0}| \, x^2`$은 기대값 회귀를 수행합니다. 매개변수 $\gamma$는 학습하려는 가치 함수의 할인 요소입니다. 실제로 우리는 두 가지 다른 유형의 목표를 사용합니다: 훈련 트래JECT로리의 마지막 상태와 훈련 배치에서 무작위로 샘플링된 목표.
더 나은 근사를 얻기 위해, 우리는 $`V_\theta`$ 정의에서 유클리드 거리를 준거로 대체하는 것을 추가로 탐구합니다. $`V^\star`$를 학습하기 위해 사용되는 준거는 제안된 일반 형태입니다.
JEPA 모델을 훈련시키는 두 가지 접근법을 고려합니다. 첫 번째 접근법은 “Sep"으로, 상태 인코더만 $`\mathcal{L}_\text{VF}`$ 목표를 사용하여 독립적으로 훈련하고, 그 후 행동 인코더와 예측자를 $`\mathcal{L}_\text{pred}`$ 손실을 사용하여 훈련합니다. 두 번째 접근법은 모든 네트워크를 함께 훈련하며 $`\mathcal{L}_\text{VF}`$ 및 $`\mathcal{L}_\text{pred}`$의 합을 목표로 합니다.
실험
실험 설정
우리는 오프라인 강화 학습 환경에서 두 개의 환경에서 실험을 수행합니다. 모델은 환경에서 샘플링된 무작위 트래JECT로리로 훈련됩니다. 모델에 입력되는 상태는 관찰 이미지이며, 추가 센서 정보가 포함될 수 있습니다. 데이터셋의 상세한 설명은 부록 7.1에 제공됩니다.
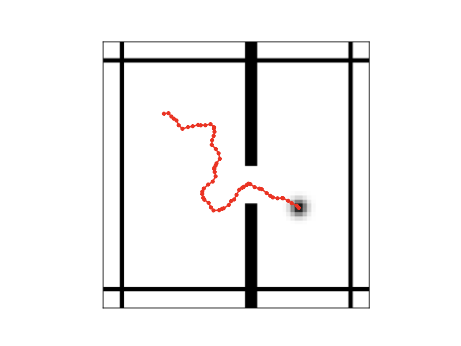
벽 환경은 벽과 문으로 구분된 정사각형 공간입니다. 환경이 인스턴스화될 때 벽과 문의 위치는 무작위로 초기화됩니다. 에이전트는 임의의 시작 위치에서 벽의 반대쪽에 있는 임의의 목표 위치로 이동해야 합니다. 그들은 이동을 나타내는 벡터에 해당하는 액션을 실행할 수 있습니다. 우리는 두 가지 설정으로 데이터셋을 생성합니다: WS는 작은 노름을 가진 액션, WB는 더 큰 노름을 가진 액션입니다.
미로 환경은 임의의 시작 위치에서 임의의 목표 위치까지 랜덤 미로 내부를 이동해야 하는 에이전트가 포함되어 있습니다. 그들의 행동은 속도 명령입니다. 이 환경에서 계획에는 에이전트의 위치와 속도 모두가 표현에 인코딩되어야 하며, 이는 관성 시뮬레이션을 나타냅니다. 비슷한 접근법을 사용하여, 우리는 상태를 위한 인코더에게 에이전트의 속도를 입력으로 포함시킵니다.
표현을 통한 계획
다른 학습 방법의 계획 성능을 평가하기 위해 실험을 수행합니다. 구체적으로, 다음과 같이 JEPA 모델을 훈련시키고 있습니다:
| 이름 |
상태 인코더 손실 |
Sep |
| 대비 |
$`\mathcal{L}_\text{contrastive}`$ |
|
| 회귀 |
$`\mathcal{L}_\text{regressive}`$ & $`\mathcal{L}_\text{VCReg}`$ |
|
| pred_VCReg |
$`\mathcal{L}_\text{VCReg}`$ |
$`\times`$ |
| pred_EMA |
EMA 절차 |
$`\times`$ |
| VF |
$`\mathcal{L}_\text{VF}`$ |
|
훈련 접근법
| 이름 |
상태 인코더 손실 |
Sep |
| VF_pred |
$`\mathcal{L}_\text{VF}`$ |
$`\times`$ |
| VF_quasi |
$`\mathcal{L}_\text{VF}`$ & 준거 |
|
| VF_quasi_pred |
$`\mathcal{L}_\text{VF}`$ & 준거 |
$`\times`$ |
| VF_VCReg |
$`\mathcal{L}_\text{VF}`$ & $`\mathcal{L}_\text{VCReg}`$ |
|
| VF_VCReg_pred |
$`\mathcal{L}_\text{VF}`$ & $`\mathcal{L}_\text{VCReg}`$ |
$`\times`$ |
훈련 접근법
실험의 세부 설정은 부록 7.2에 설명되어 있습니다.
우리는 학습된 표현의 품질을 평가하기 위해 모델의 계획 정확성을 평가합니다. 이는 임의의 초기 상태와 목표 쌍에 대한 성공적인 계획 비율로 정의됩니다. 우리는 200개의 벽 환경 인스턴스와 80개의 미로 환경 인스턴스에서 이를 계산하여 결과의 분산이 작아지도록 합니다. MPC 절차에 MPPI 최적화기를 사용합니다. 결과는 표 4에 표시됩니다.
| 유형 |
WS |
WB |
미로 |
| 대비 |
0.49 |
0.59 |
0.50 |
| 회귀 |
0.54 |
0.57 |
0.46 |
| pred_VCReg |
0.55 |
0.89 |
0.54 |
| pred_EMA |
0.46 |
0.43 |
0.04 |
| VF |
0.63 |
0.94 |
0.49 |
다양한 환경에서의 계획 결과
| 유형 |
WS |
WB |
미로 |
| VF_pred |
0.55 |
0.75 |
0.49 |
| VF_quasi |
0.71 |
0.96 |
0.63 |
| VF_quasi_pred |
0.61 |
0.85 |
0.43 |
| VF_VCReg |
0.49 |
0.75 |
0.39 |
| VF_VCReg_pred |
0.47 |
0.67 |
0.39 |
다양한 환경에서의 계획 결과
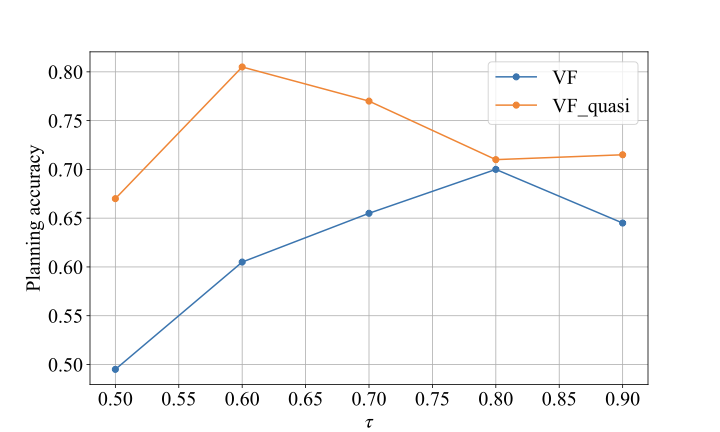
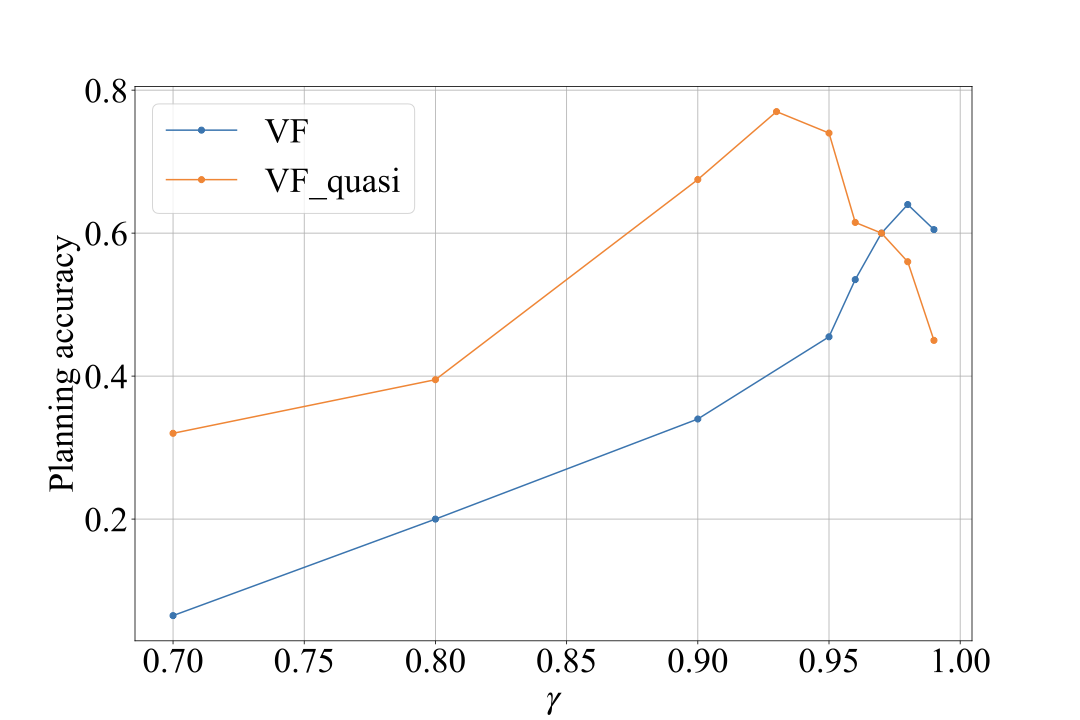
결과는 IQL 접근법이 계획 중 유용한 안내를 제공하고 예측 기반 접근법보다 더 나은 성능을 보여줍니다. 흥미롭게도, VF_quasi 접근법은 이론적인 가치 함수가 대칭적일지라도 일관되게VF 접근법보다 우수합니다. 이를 통해 준거는 네트워크의 표현력을 높이므로 훈련 과정을 용이하게 한다는 것을 시사합니다.
예측 손실과 IQL 손실을 모두 사용하여 표현을 학습하는 것은 단독으로 IQL 손실만 사용하는 것보다 효과적이지 않습니다. VCReg를 사용하여 IQL 손실로 학습할 때 다양성을 촉진하더라도 계획 성능이 좋지 않습니다. WB 데이터셋에서 얻은 결과가 WS 데이터셋에서 얻은 결과보다 우수합니다. 이는 단일 트래JECT로리가 WB 데이터셋에서는 환경을 더 많이 탐색하고 에이전트가 벽과 충돌할 가능성이 높기 때문입니다.
논의
훈련의 지역성: 불완전한 결과는 우리의 접근법으로 학습된 가치 함수가 정확하지 않다는 것을 나타냅니다. 상태 간에 로컬 관계를 올바르게 포착할 수 있지만, 먼 거리 관계는 두 가지 주요 이유로 덜 가능합니다. 첫째, 훈련 중 먼 삼중 상태(시작 상태, 다음 상태 및 목표)의 공간은 희박하게 샘플링됩니다. 둘째, 상태가 주어진 목표로부터 멀리 있을 때 가치 함수에 대한 상태에 대한 경사도는 작아집니다. 그런 상태에서는 가치 함수의 신호 대 잡음 비율이 낮습니다. 이는 표현 공간 계층을 사용하여 긴 거리를 모델링하거나 더 적게 샘플링된 트래JECT로리를 통해 먼 관계를 포착하고 개선된 결과를 얻을 수 있음을 시사합니다.
데이터셋의 영향: IQL 손실에 대한 이론적 결과는 $`\tau`$가 1에 가까워질 때 실제로 훈련 데이터셋을 생성하는 정책의 지지만 중요하다고 나타냅니다. 그러나 실제에서는 다른 요인이 관련될 가능성이 있습니다. 매우 서브옵티멀한 트래JECT로리에서 서로 근접한 상태는 멀리 떨어져 보일 수 있어 학습이 더 어려울 수 있습니다. 따라서 “전문가” 트래JECT로리를 사용하는 것이 좋을 수 있지만, 이들은 다양성과 탐색에 대한 비용을 치르며 얻기 어렵습니다. 또한, IQL 손실에서 훈련 중 상태를 전체 상태 공간을 포괄하도록 하는 것이 중요합니다. 실제로 이를 달성하기 위해서는 더 큰 학습 데이터셋 크기를 증가시키거나 효과적인 데이터 수집 전략을 사용해야 합니다.
결론
본 연구에서는 JEPA 세계 모델의 계획 능력을 향상시키려고 시도했습니다. 이를 위해 상태 인코더를 학습하여 표현 공간에서 유클리드 거리 또는 준거가 주어진 목표 도달 비용과 관련된 음의 목표 조건 가치 함수를 근사하도록 강화했습니다. 이는 JEPA 모델의 상태 인코더를 암시적 Q 학습(IQL) 손실을 사용하여 학습함으로써 달성되었습니다.
우리는 이러한 방법들을 직관적인 접근법 및 표준 예측 기반 JEPA 훈련 접근법과 비교하여 벤치마크 행동 계획 작업에서 실험했습니다. 우리의 결과는 가치 함수 기반 방법, 특히 준거를 사용하는 것이 우수함을 보여줍니다.