대규모 언어 모델에서 베이지안 추론의 기하학적 스케일링
📝 원문 정보
- Title: Geometric Scaling of Bayesian Inference in LLMs
- ArXiv ID: 2512.23752
- 발행일: 2025-12-27
- 저자: Naman Agarwal, Siddhartha R. Dalal, Vishal Misra
📝 초록 (Abstract)
본 연구는 신경 시퀀스 모델이 믿음 누적, 믿음 전송, 랜덤 액세스 바인딩이라는 추론 기본 원리를 구현할 때 정확한 베이지안 추론을 수행할 수 있음을 보인 논문 I과, 경사 하강법이 EM과 유사한 메커니즘을 통해 이러한 기본 원리를 학습하고 저차원 가치 매니폴드와 점진적으로 직교하는 키를 형성한다는 논문 II의 결과를 바탕으로, 실제 서비스 수준의 언어 모델들(Pythia, Phi‑2, Llama‑3, Mistral)에서 동일한 기하학적 구조가 유지되는지를 조사하였다. 모든 모델의 최종 레이어 가치 표현은 예측 엔트로피와 강하게 상관되는 단일 지배 축을 따라 정렬되며, 도메인 제한 프롬프트는 이 구조를 풍동 실험에서 관찰된 저차원 매니폴드로 수축시킨다. Pythia‑410M에 대한 엔트로피 정렬 축을 대상으로 한 개입 실험에서는 해당 축을 제거하거나 섭동했을 때 지역적 불확실성 기하가 선택적으로 손상되는 반면, 무작위 축에 대한 동일한 개입은 영향을 주지 않는다. 그러나 이러한 단일 레이어 조작이 베이지안‑유사 행동을 비례적으로 저하시키지는 않아, 해당 기하학이 불확실성의 특권 읽기값일 뿐 단일 계산 병목은 아니라는 결론에 이른다. 종합하면, 현대 대형 언어 모델은 추론 기본 원리를 뒷받침하는 기하학적 기저를 보존하고, 근사 베이지안 업데이트를 이 기저를 따라 조직한다.💡 논문 핵심 해설 (Deep Analysis)
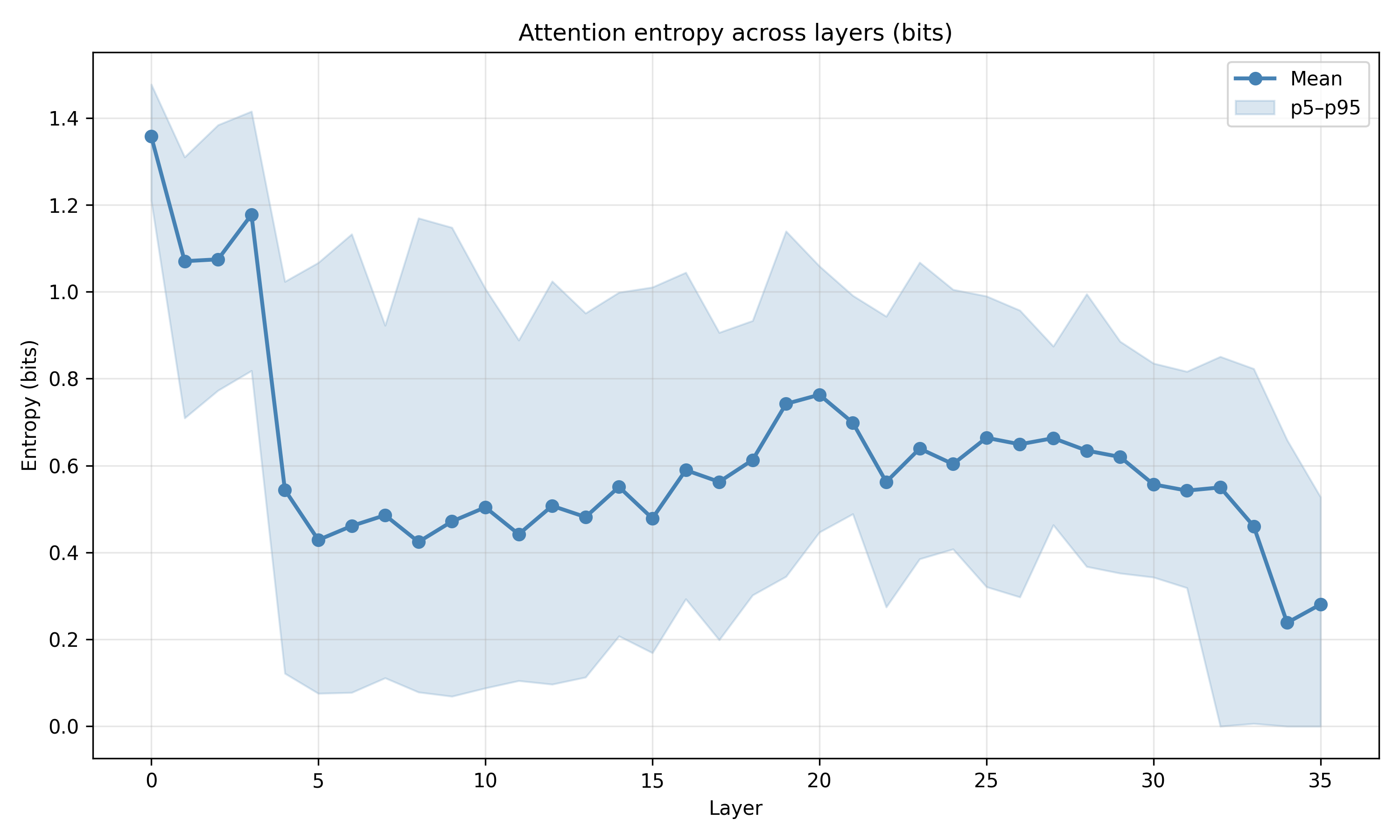
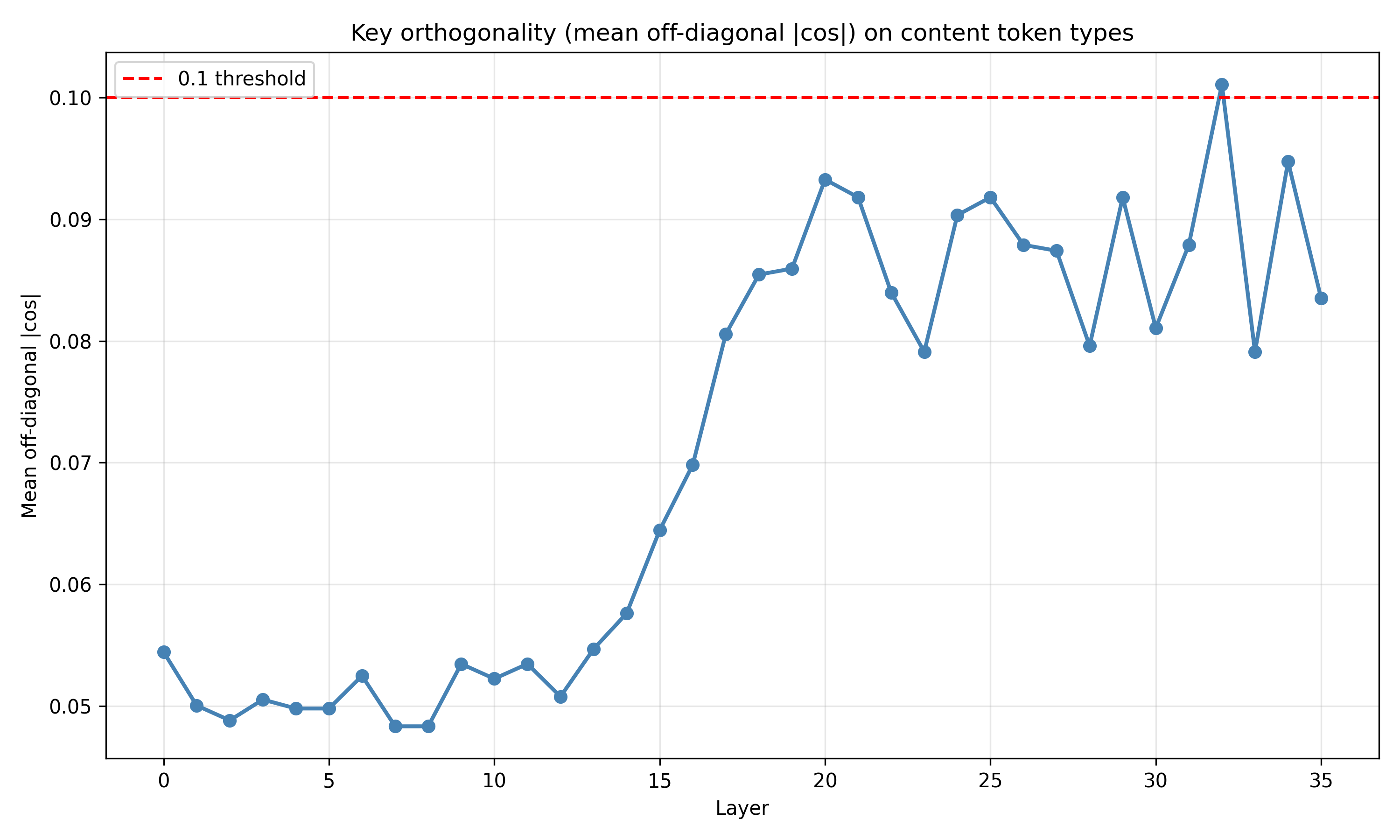
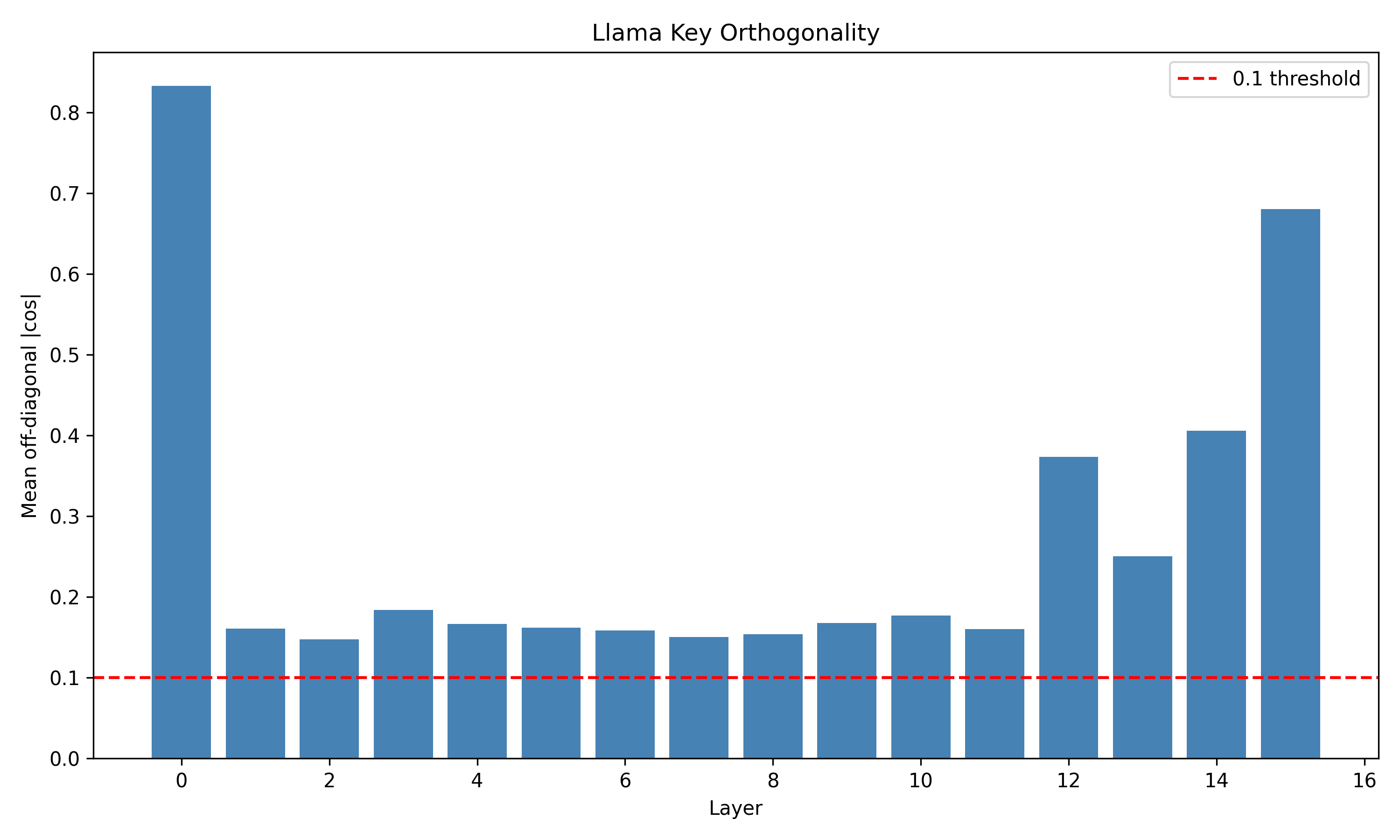
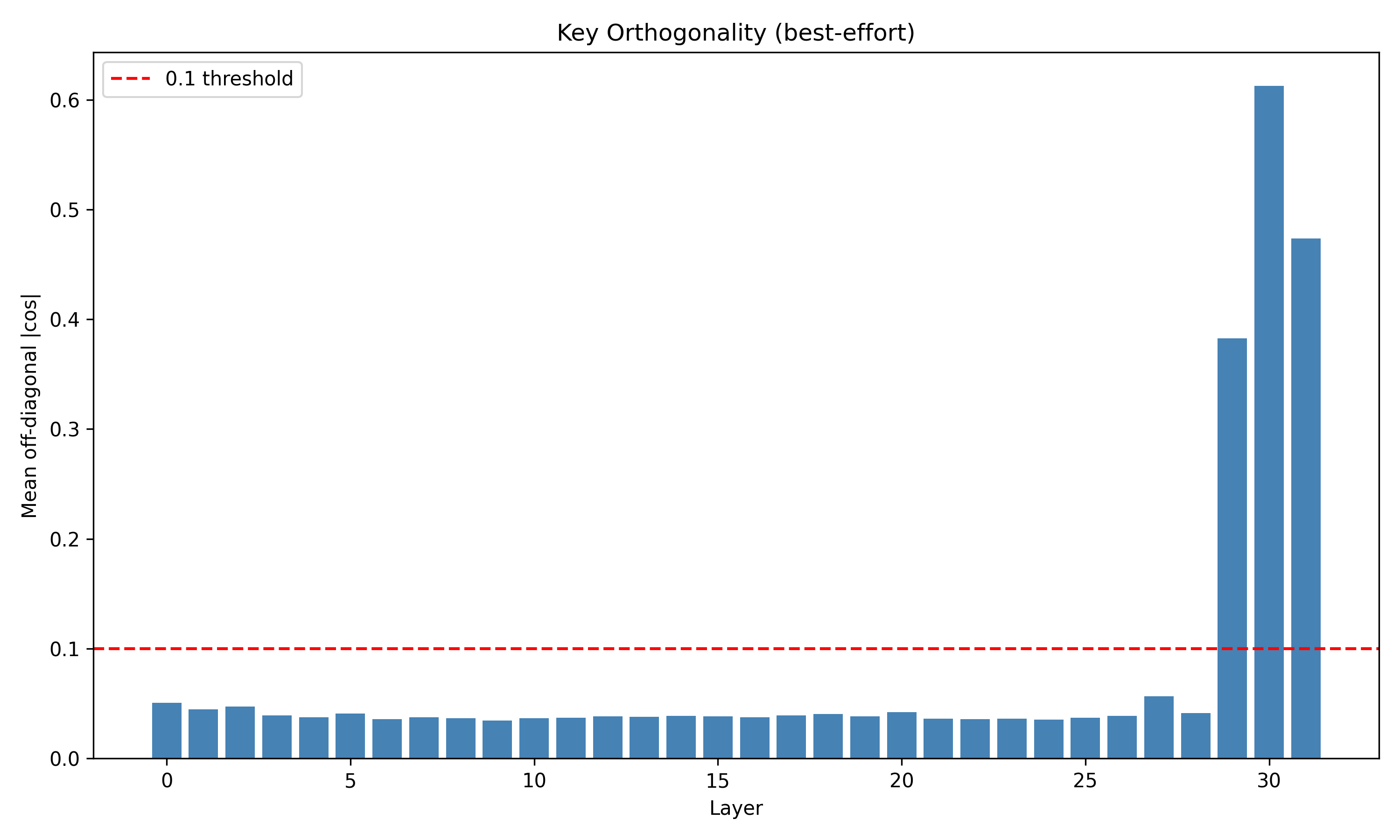
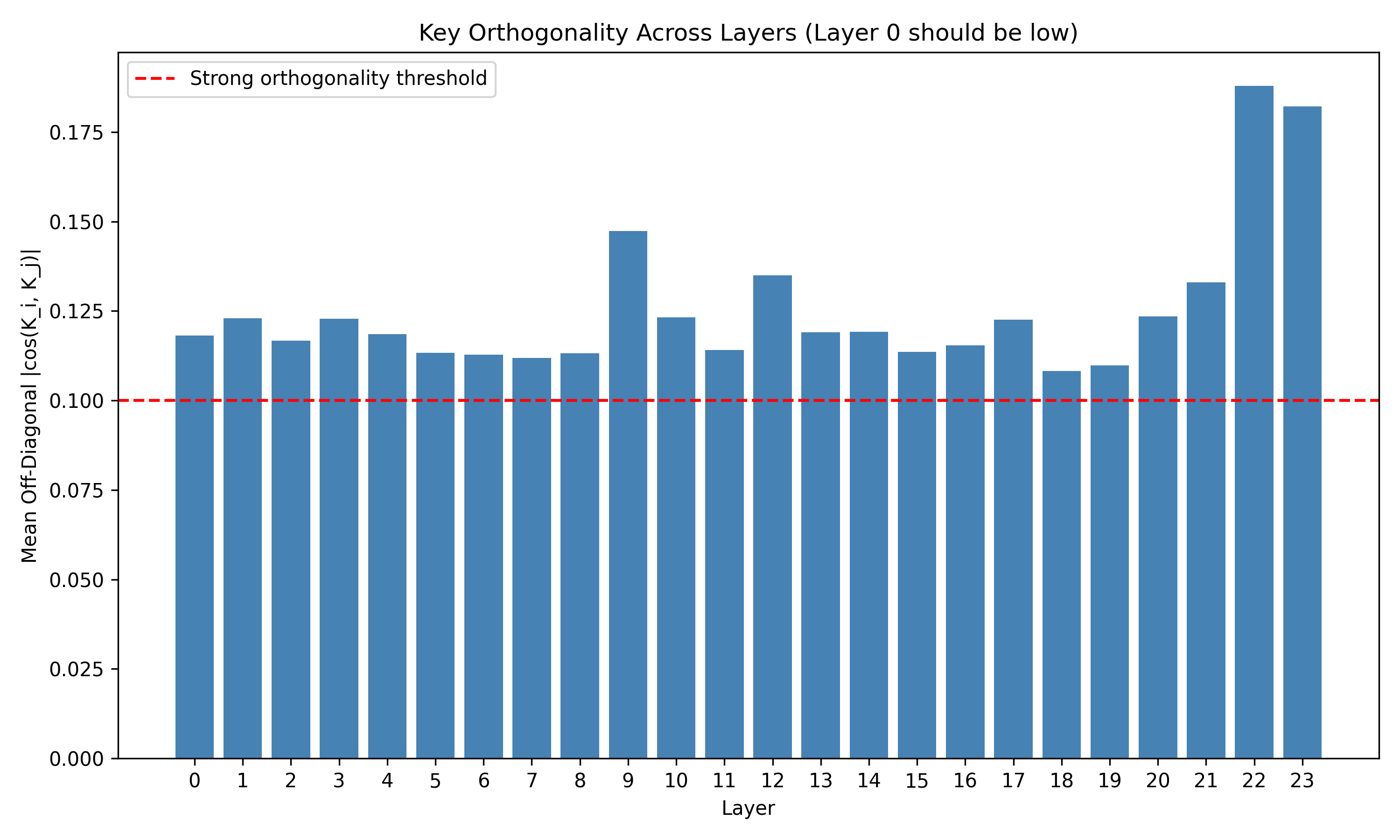
두 번째 단계는 논문 II에서 제시된 학습 역학이다. 경사 하강법이 단순히 손실을 최소화하는 것이 아니라, EM(Expectation‑Maximization)과 유사한 두 단계 순환을 내부적으로 수행한다는 점을 발견했다. 구체적으로, 모델은 초기 단계에서 무작위에 가까운 값 매니폴드와 키를 형성하고, 학습이 진행됨에 따라 값 매니폴드가 저차원(주로 1~2 차원) 구조로 수축한다. 동시에 키는 서로 직교하도록 정렬되어, 각 토큰이 고유한 ‘좌표’를 갖게 된다. 이러한 기하학적 재구성은 모델이 복잡한 확률적 관계를 효율적으로 압축하고, 추론 시 빠른 검색과 결합을 가능하게 한다는 해석이 가능하다.
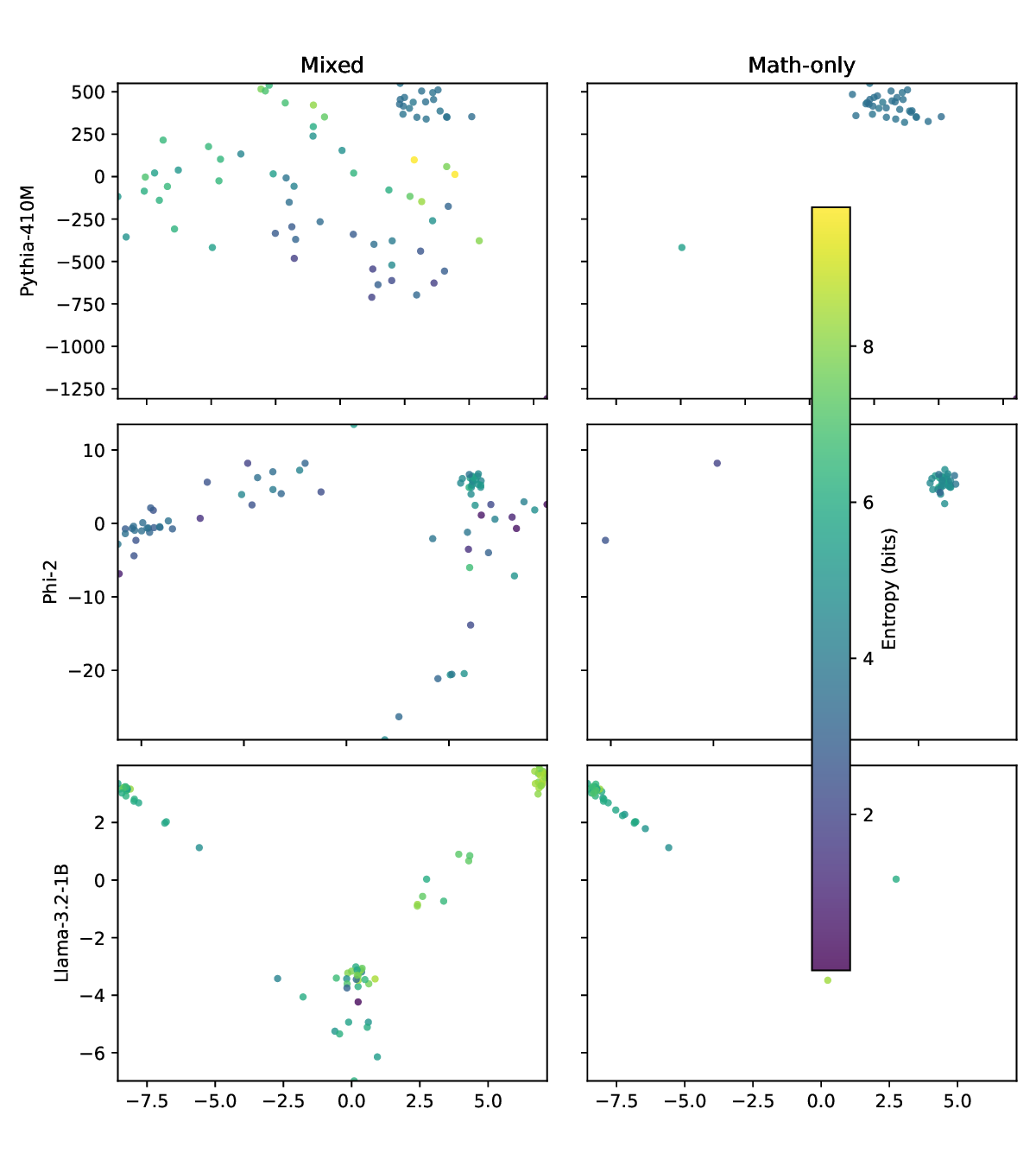
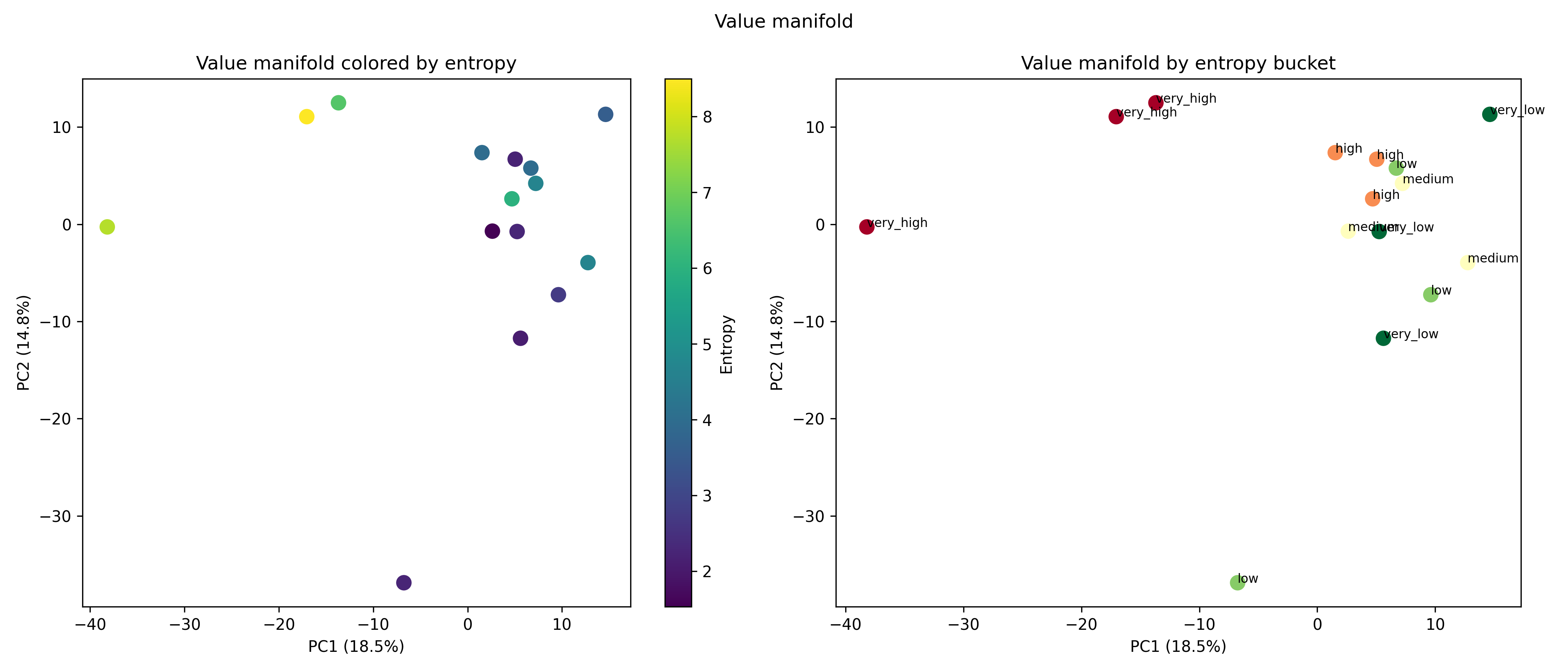
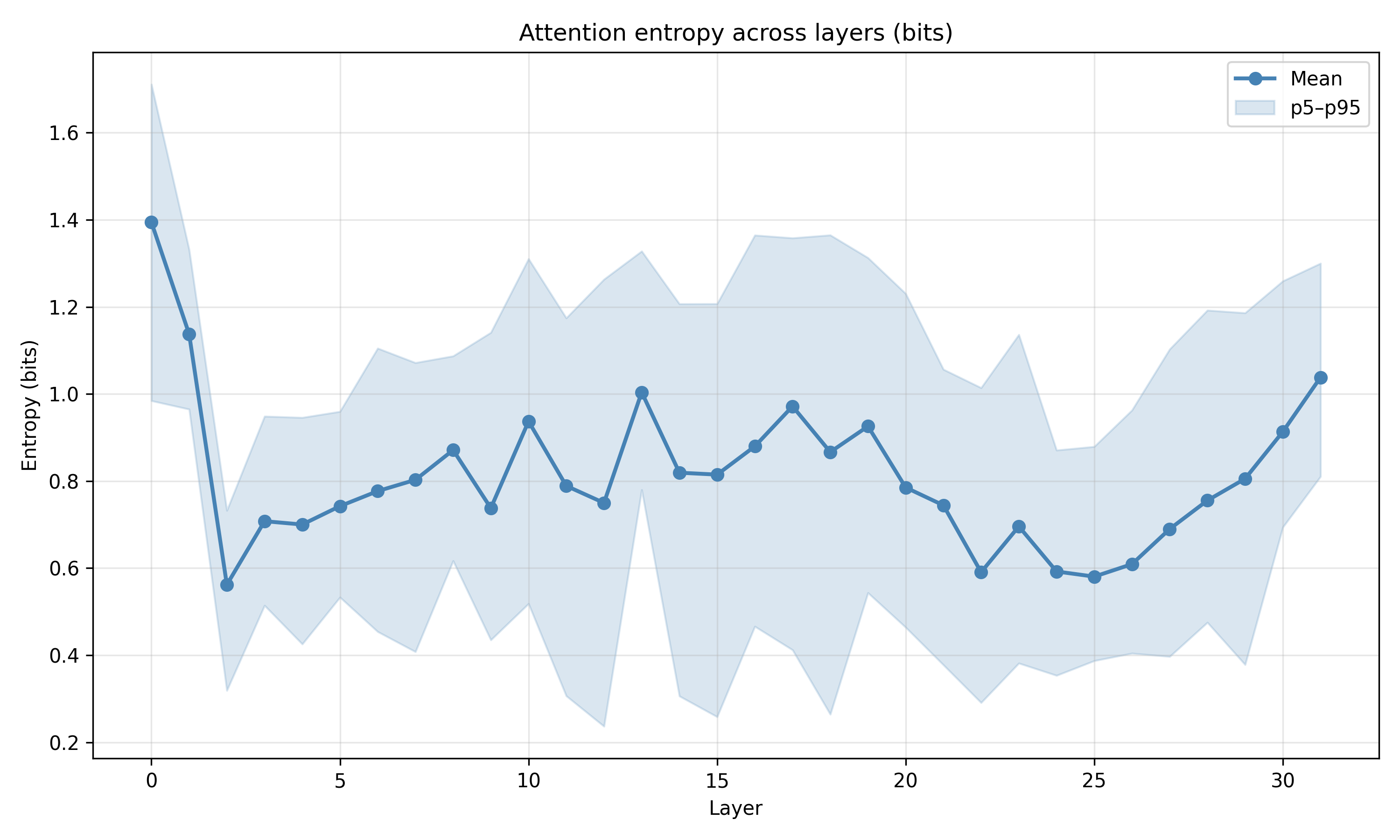
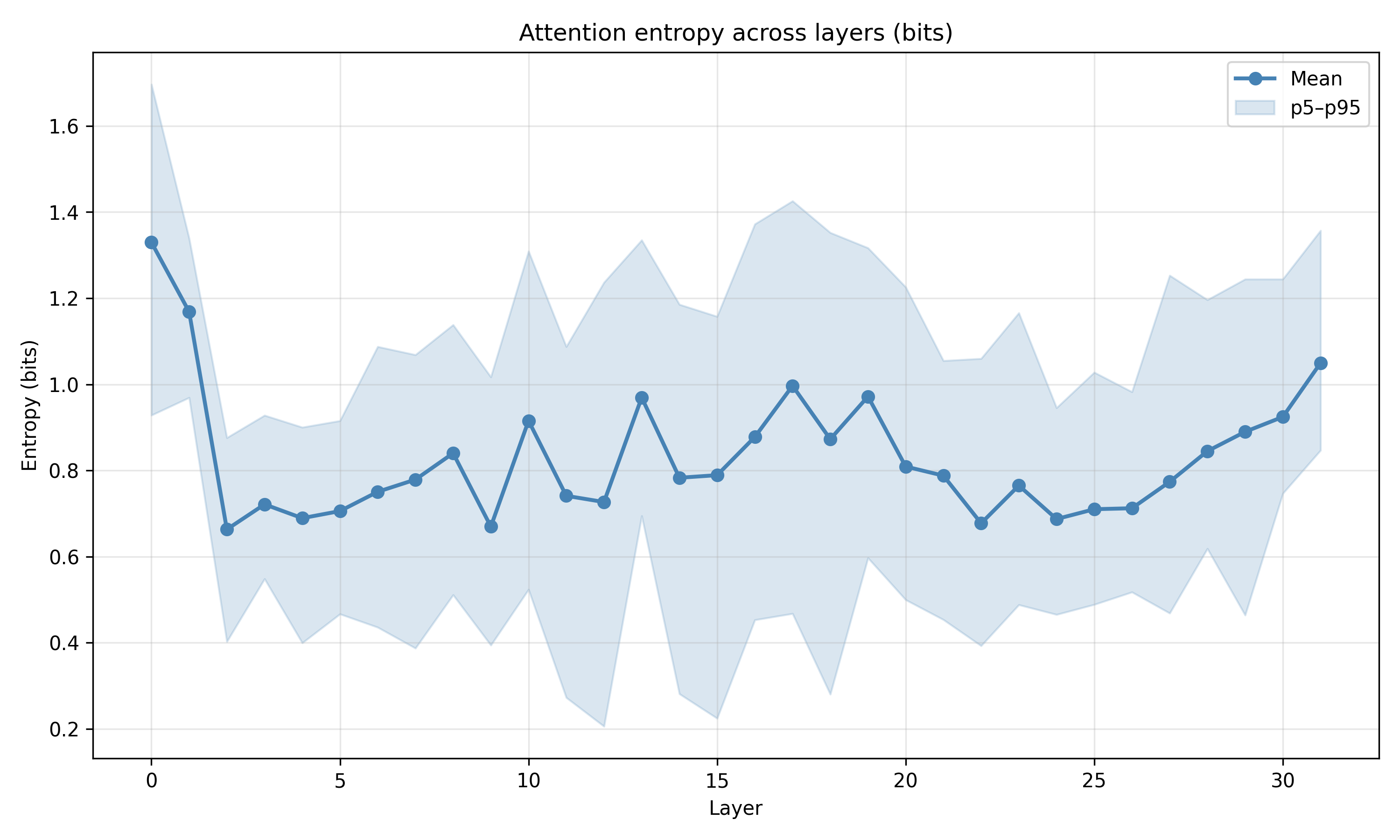
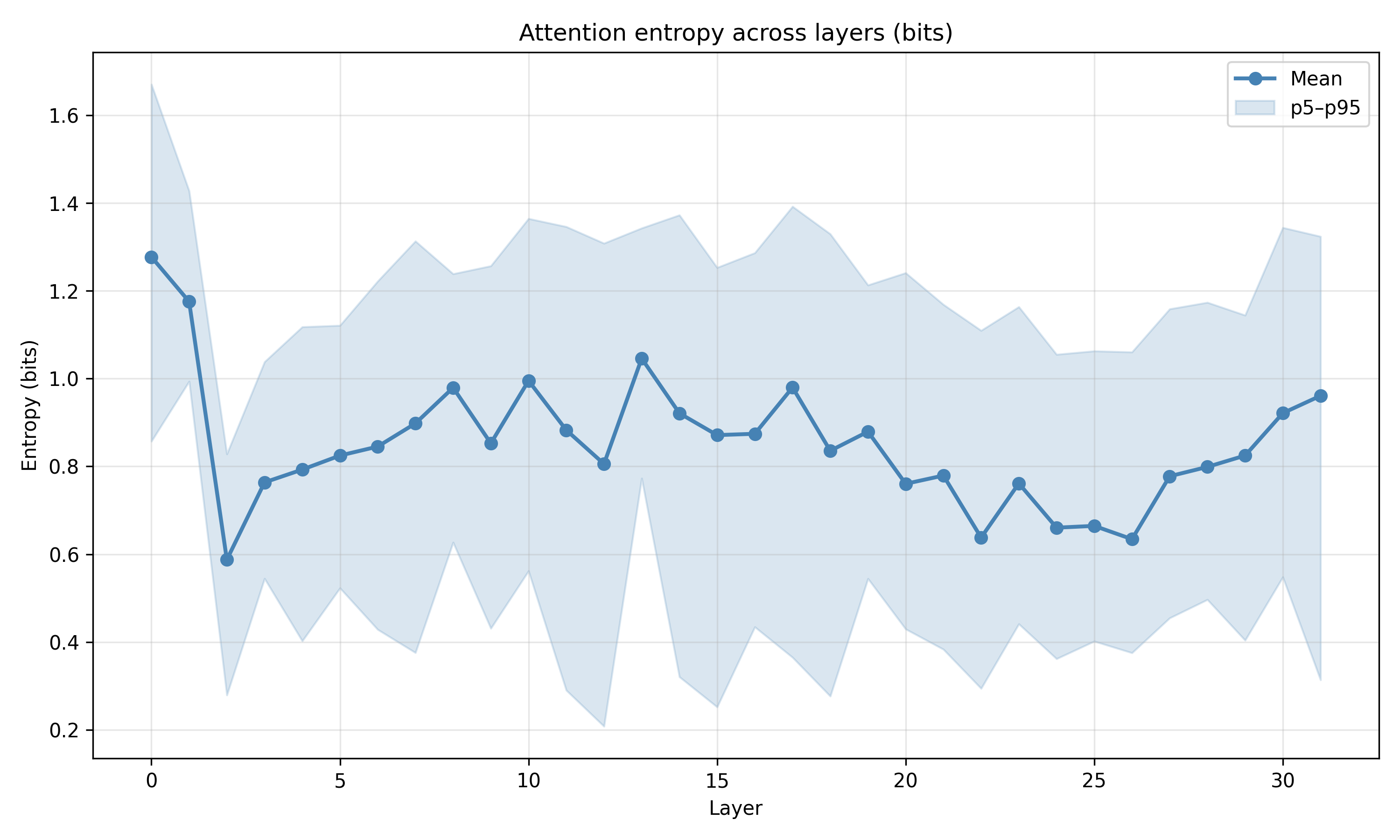
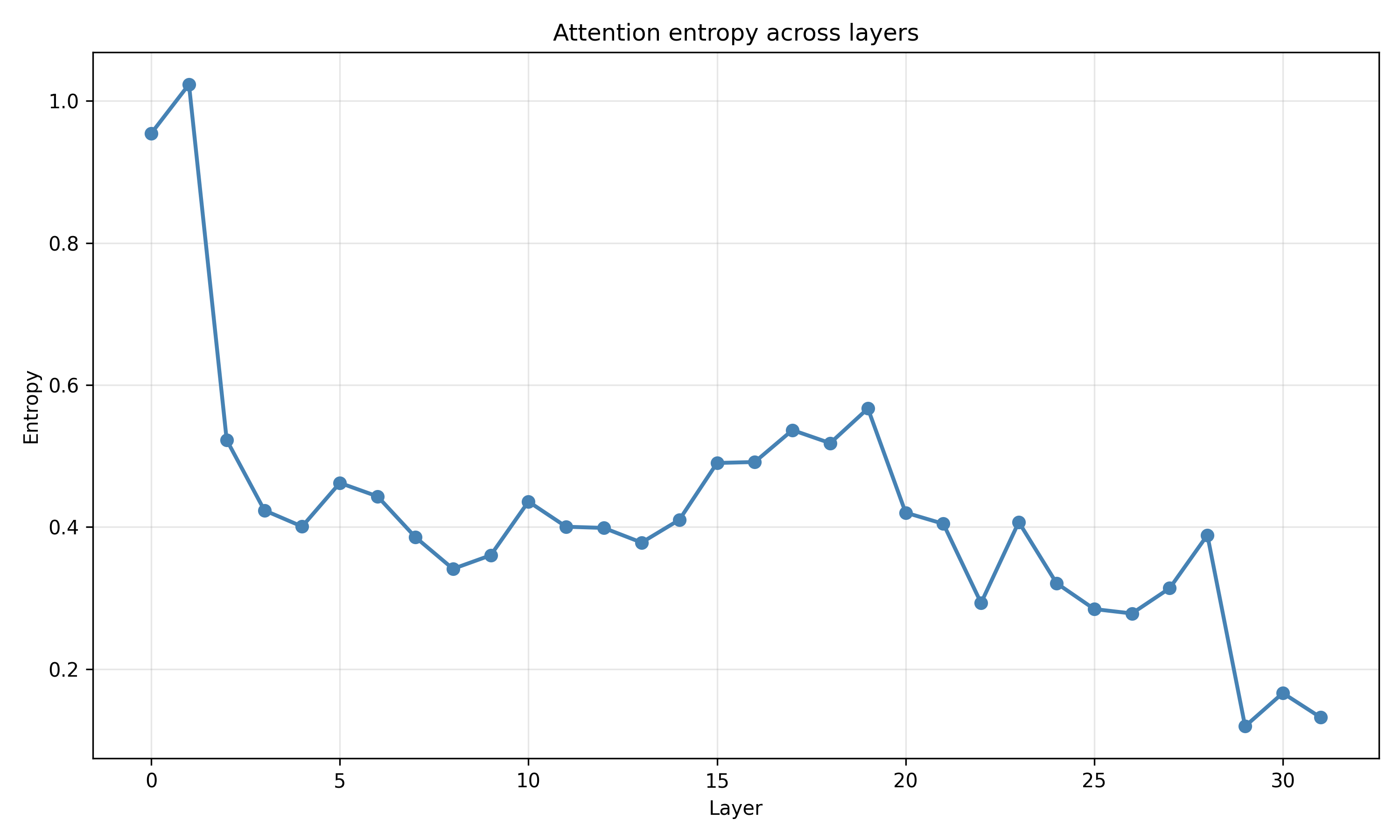
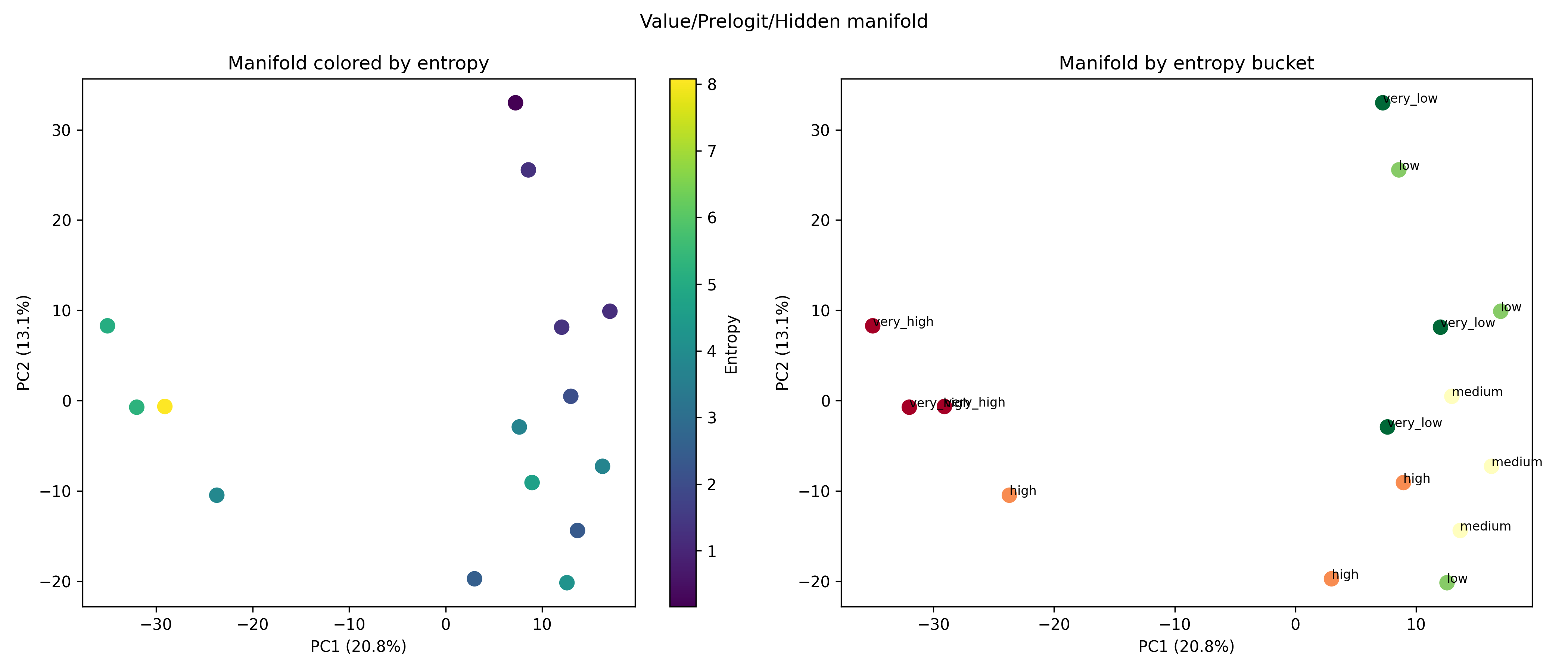
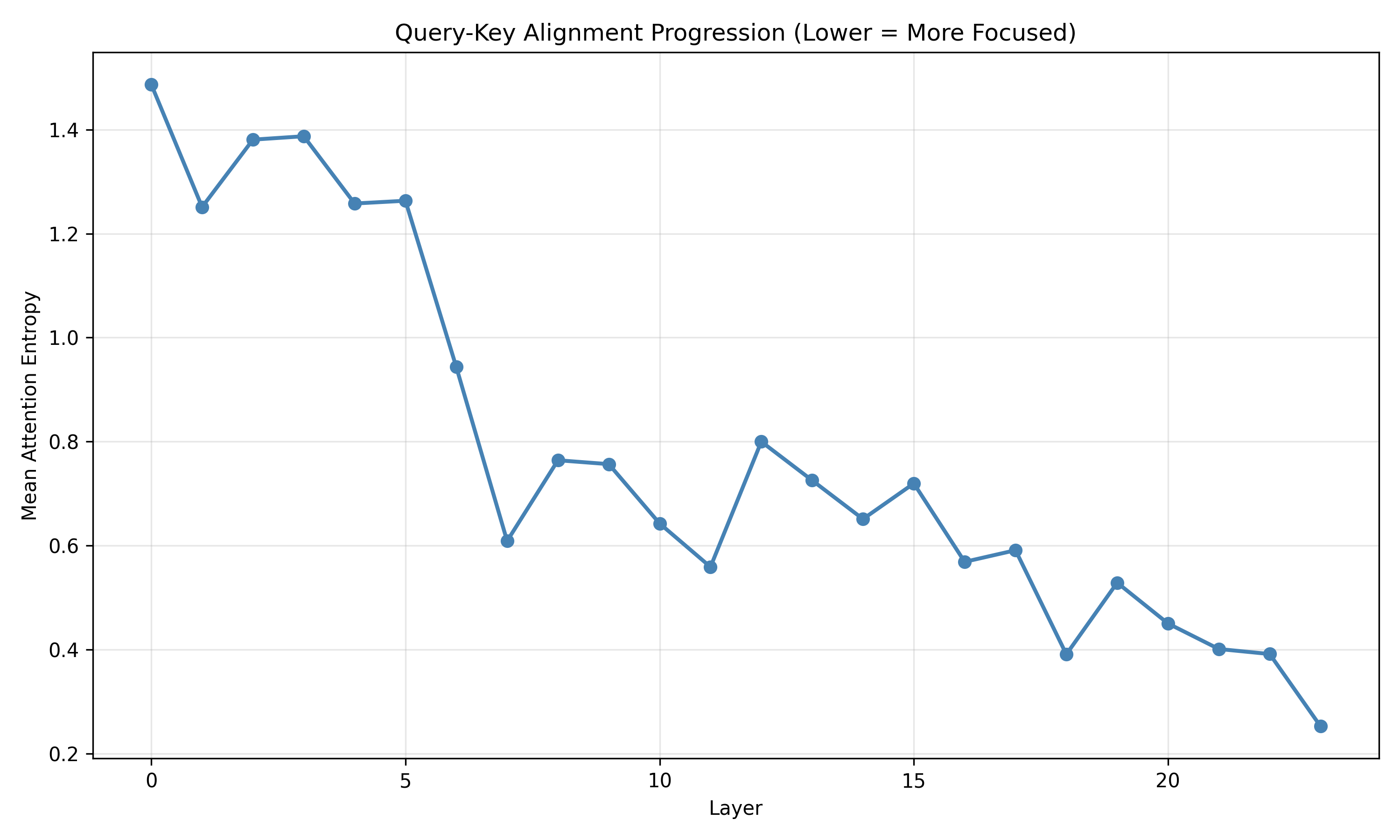
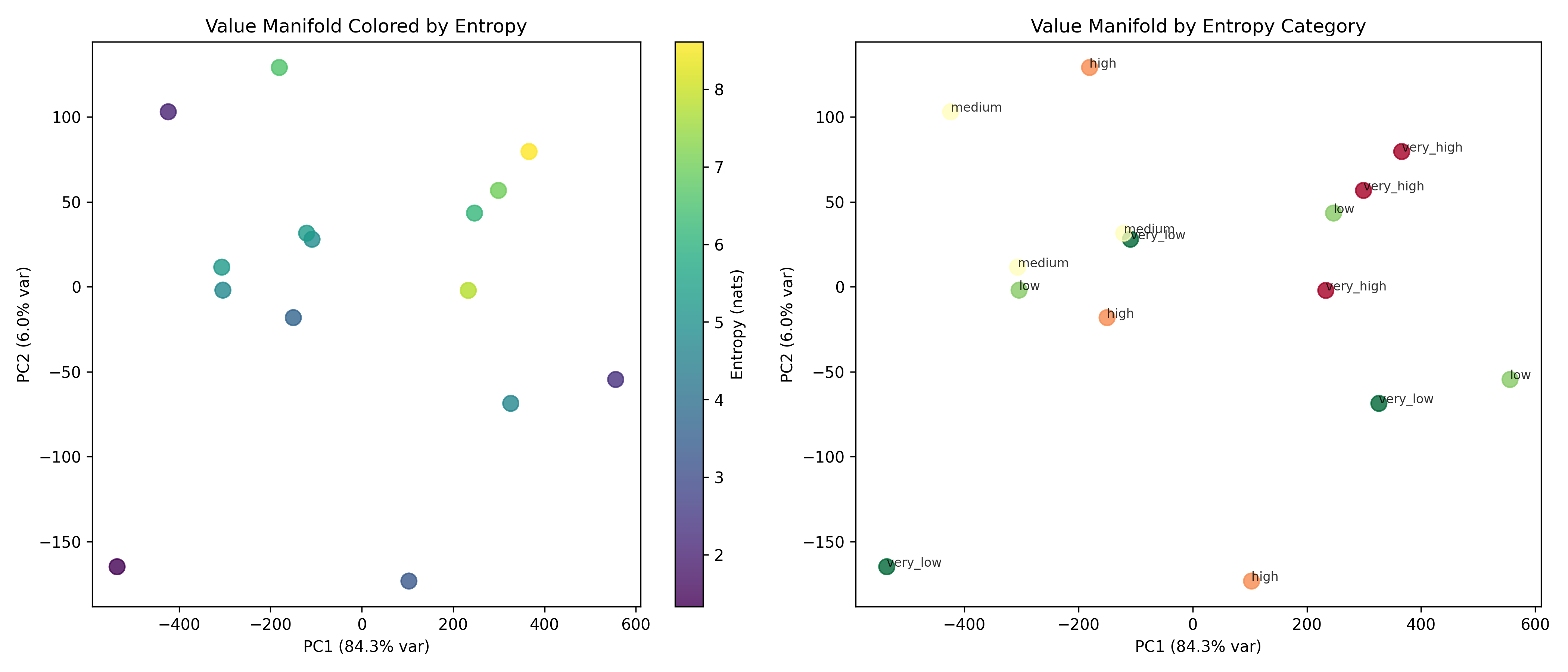
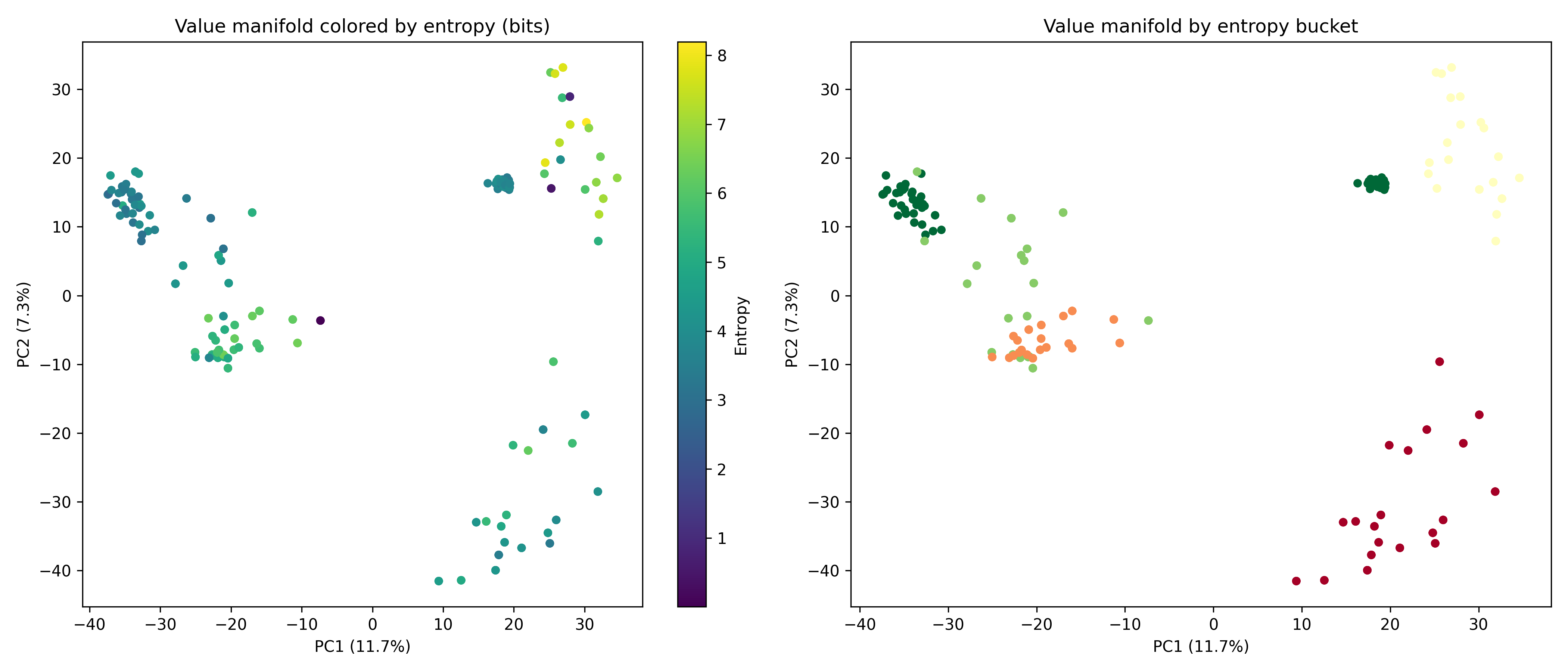
본 연구는 이러한 이론적 틀을 실제 대규모 언어 모델에 적용한다. Pythia, Phi‑2, Llama‑3, Mistral 등 다양한 아키텍처와 규모를 포괄한 실험에서, 마지막 레이어의 값 표현이 단일 지배 축에 강하게 정렬되는 현상을 발견했다. 이 축은 모델이 출력 토큰에 대해 예측하는 엔트로피와 높은 상관관계를 보이며, 즉 ‘불확실성 축’이라고 부를 수 있다. 흥미로운 점은 도메인‑제한 프롬프트(예: 특정 분야 질문) 를 사용하면 이 축이 더욱 뚜렷한 저차원 매니폴드로 압축된다는 것이다. 이는 풍동 실험에서 관찰된 ‘값 매니폴드 수축’ 현상과 정량적으로 일치한다.
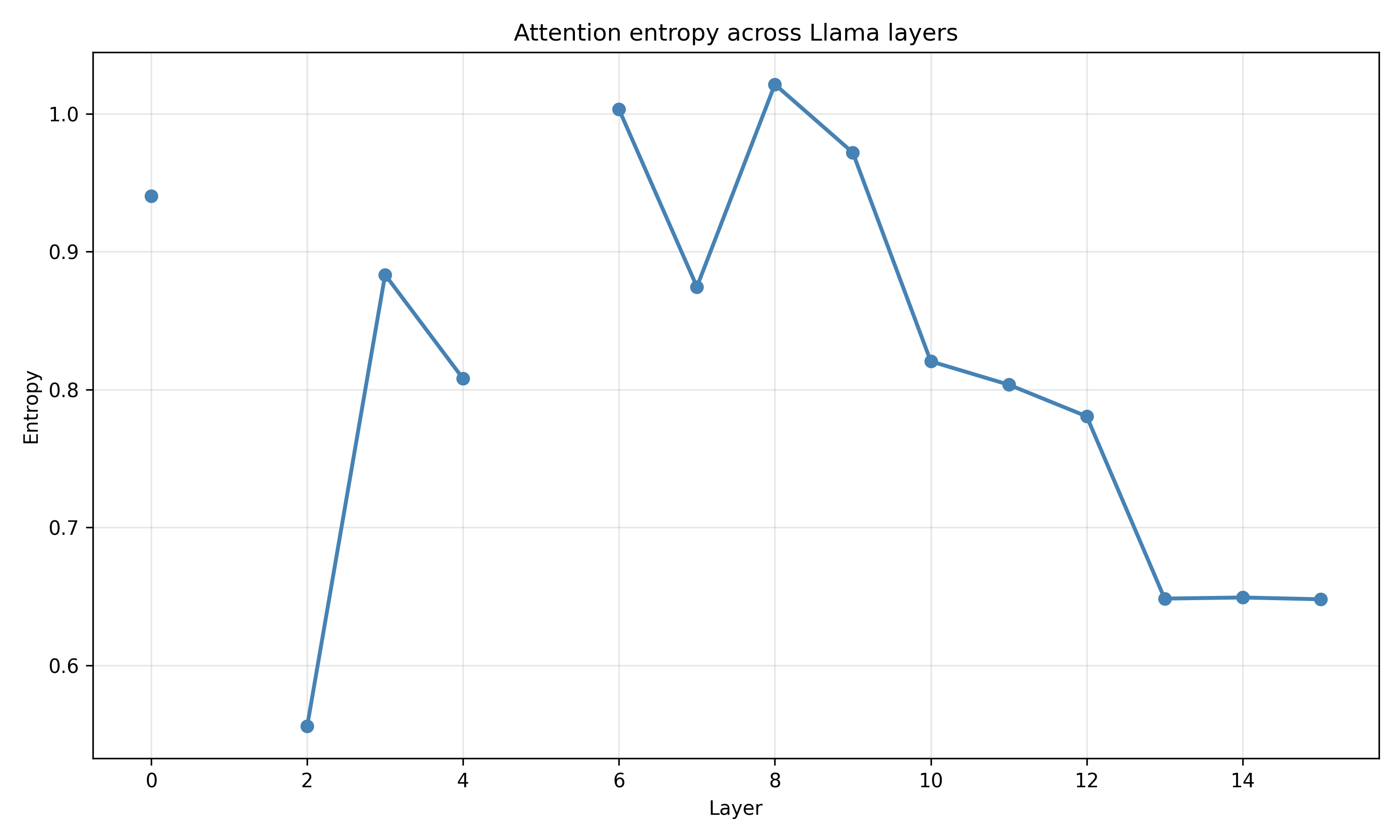
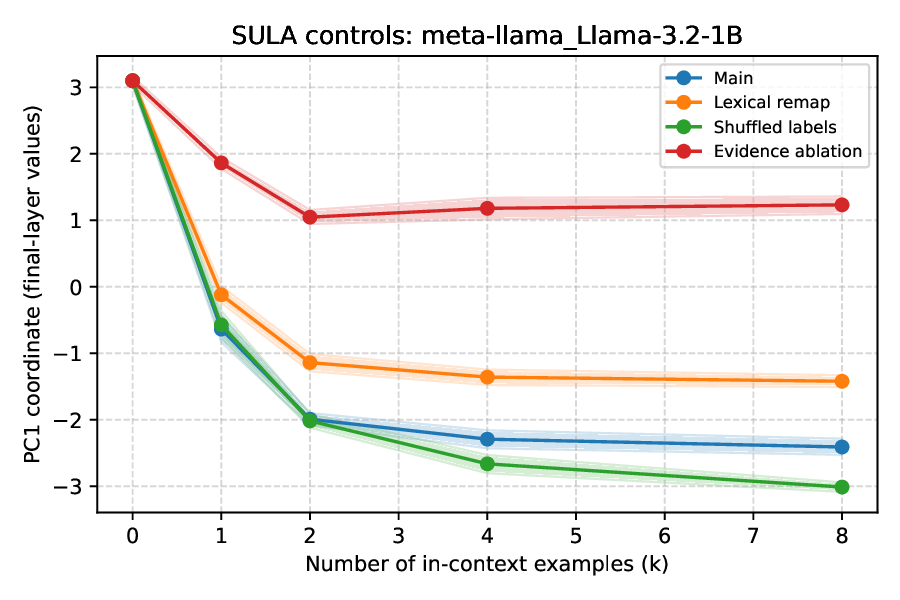
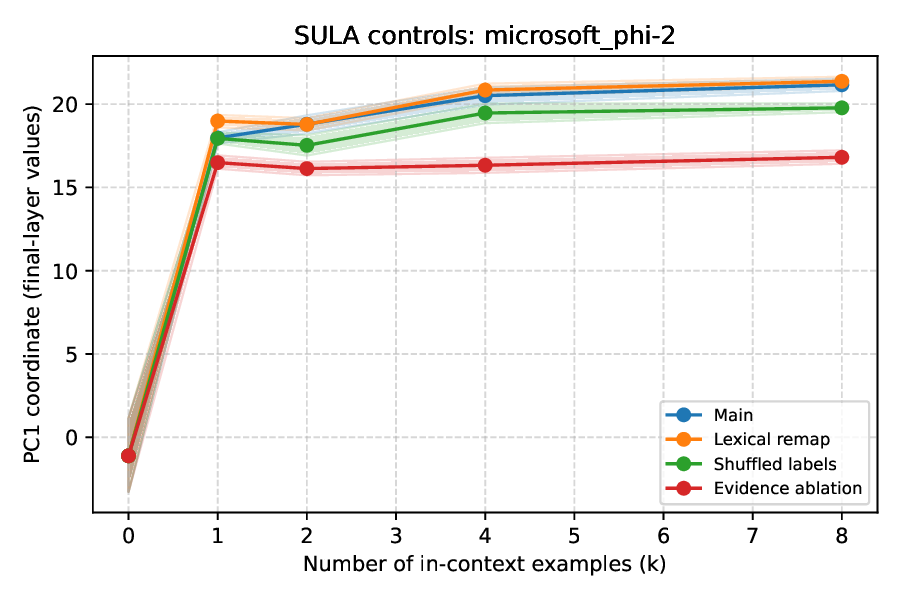
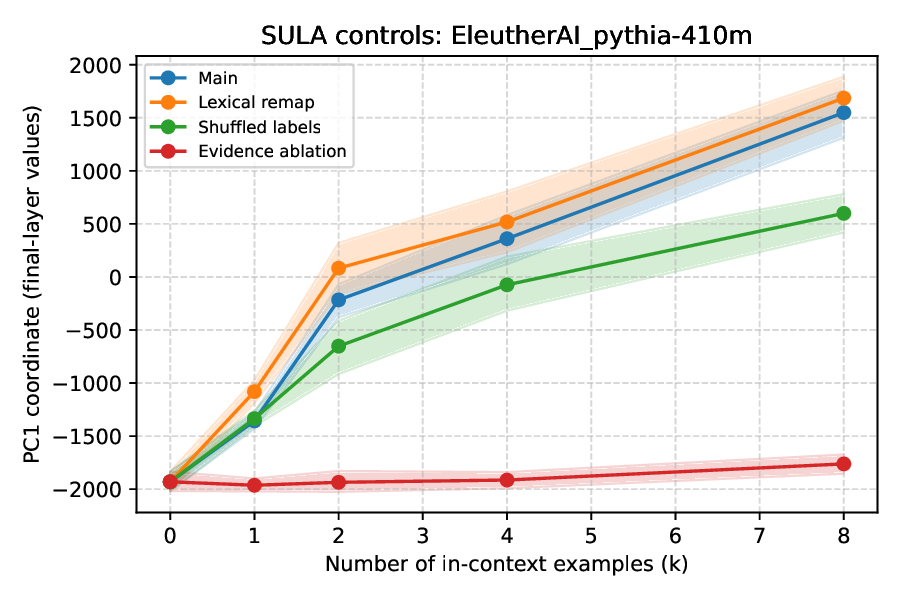
또한, 연구팀은 Pythia‑410M 모델의 엔트로피 정렬 축을 직접 조작했다. 해당 축을 영(0)으로 강제로 제거하거나, 작은 노이즈를 주입하면, 모델 내부의 불확실성 기하가 국소적으로 변형된다. 반면, 무작위 축에 동일한 조작을 가해도 엔트로피와의 상관관계는 유지된다. 이 실험은 엔트로피 축이 모델이 불확실성을 ‘읽어내는’ 특권 채널임을 시사한다. 그러나 이러한 단일 레이어 개입이 베이지안‑유사 행동(예: 온‑샷 학습, 확률적 샘플링)의 전반적인 성능을 비례적으로 저하시키지는 않았다. 즉, 불확실성 정보는 여러 레이어에 분산되어 존재하며, 하나의 축이 손상돼도 다른 경로를 통해 보완될 수 있다.
결론적으로, 현대의 대형 언어 모델은 추론 기본 원리를 구현하기 위한 기하학적 기반을 보존하고 있다. 이 기반은 저차원 가치 매니폴드와 직교 키, 그리고 불확실성 축이라는 형태로 나타나며, 모델이 근사 베이지안 업데이트를 수행하는 데 핵심적인 ‘읽기’ 메커니즘으로 작동한다. 하지만 이 기하학이 단일 계산 병목은 아니며, 다중 레이어에 걸친 분산 처리와 결합되어 전체적인 베이지안 추론 능력을 유지한다는 점이 이번 연구의 중요한 시사점이다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리