언어모델의 추론능력 향상: 잘못된 최종답안에도 불구하고 합성 데이터를 통한 개선
📝 원문 정보
- Title: Shape of Thought: When Distribution Matters More than Correctness in Reasoning Tasks
- ArXiv ID: 2512.22255
- 발행일: 2025-12-24
- 저자: Abhranil Chandra, Ayush Agrawal, Arian Hosseini, Sebastian Fischmeister, Rishabh Agarwal, Navin Goyal, Aaron Courville
📝 초록 (Abstract)
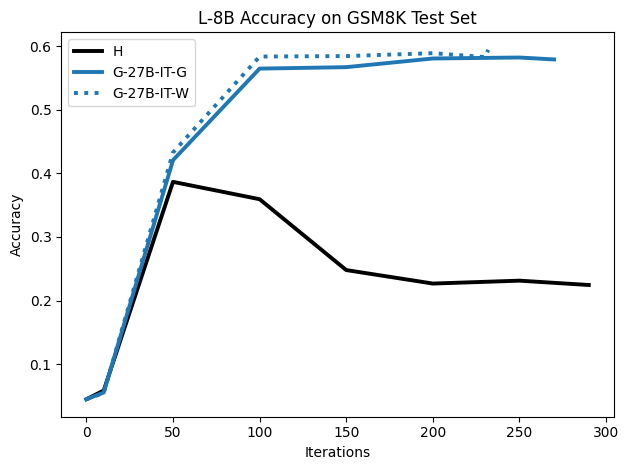
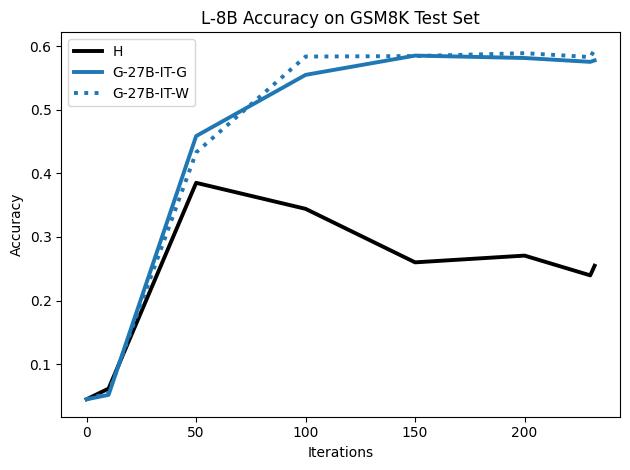
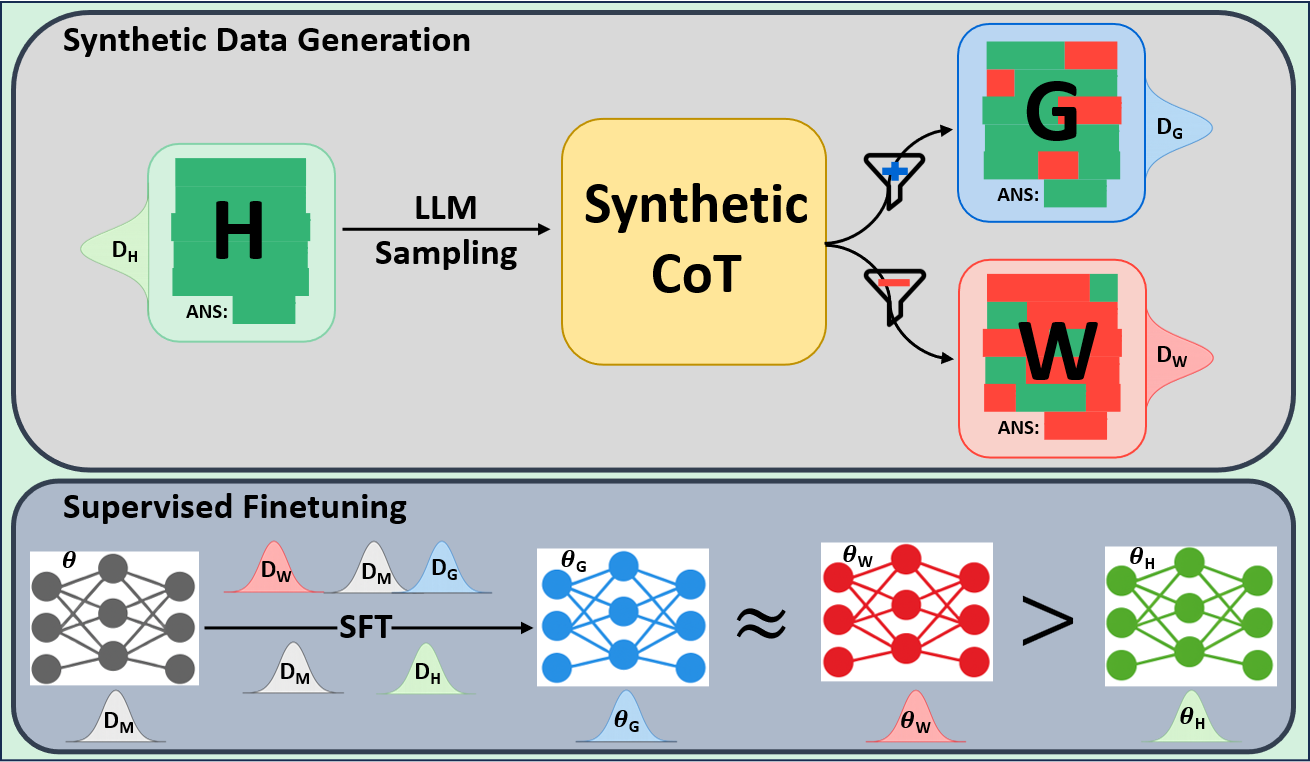
우리는 언어 모델의 추론 능력을 합성 데이터셋을 통해 향상시킬 수 있다는 놀라운 발견을 제시합니다. 이 합성 데이터셋은 더 우수한 모델에서 생성된 사슬형 사고(CoT) 추적을 포함하며, 모든 추적이 잘못된 최종 답안으로 이어지더라도 성능이 향상됩니다. 우리의 실험 결과는 이러한 접근법이 인간 주석 데이터셋에 대한 학습보다 더 나은 추론 작업 성능을 제공할 수 있음을 보여줍니다. 우리는 이를 설명하는 두 가지 주요 요인을 제안합니다: 첫째, 합성 데이터의 분포가 언어 모델 자체의 분포와 더 가깝기 때문에 학습이 용이하다는 점입니다. 둘째, 이러한 '잘못된' 추적은 종종 부분적으로 잘못되었지만 유효한 사고 단계를 포함하고 있어 모델이 이를 통해 배울 수 있다는 점입니다. 첫 번째 가설을 검증하기 위해 언어 모델을 사용하여 인간 주석 추적을 문장 변환하여 분포를 모델의 분포에 더 가깝게 이동시키고 성능 향상을 보여줍니다. 두 번째 가설을 검증하기 위해 점점 더 잘못된 CoT 추적을 도입하고 모델이 이러한 결함에 얼마나 견딜 수 있는지 연구합니다. 우리는 MATH, GSM8K, Countdown 및 MBPP 데이터셋을 사용하여 다양한 언어 모델(Qwen, Llama, Gemma)에서 1.5B에서 9B 사이의 크기로 이 발견을 여러 추론 영역(수학, 알고리즘적 사고, 코드 생성 등)에 걸쳐 보여줍니다. 우리의 연구는 데이터셋이 모델의 분포에 더 가깝게 구성되는 것이 중요한 측면임을 입증합니다. 또한 정확한 최종 답안은 항상 신뢰할 수 있는 충실한 추론 과정의 지표가 아님을 보여줍니다.💡 논문 핵심 해설 (Deep Analysis)
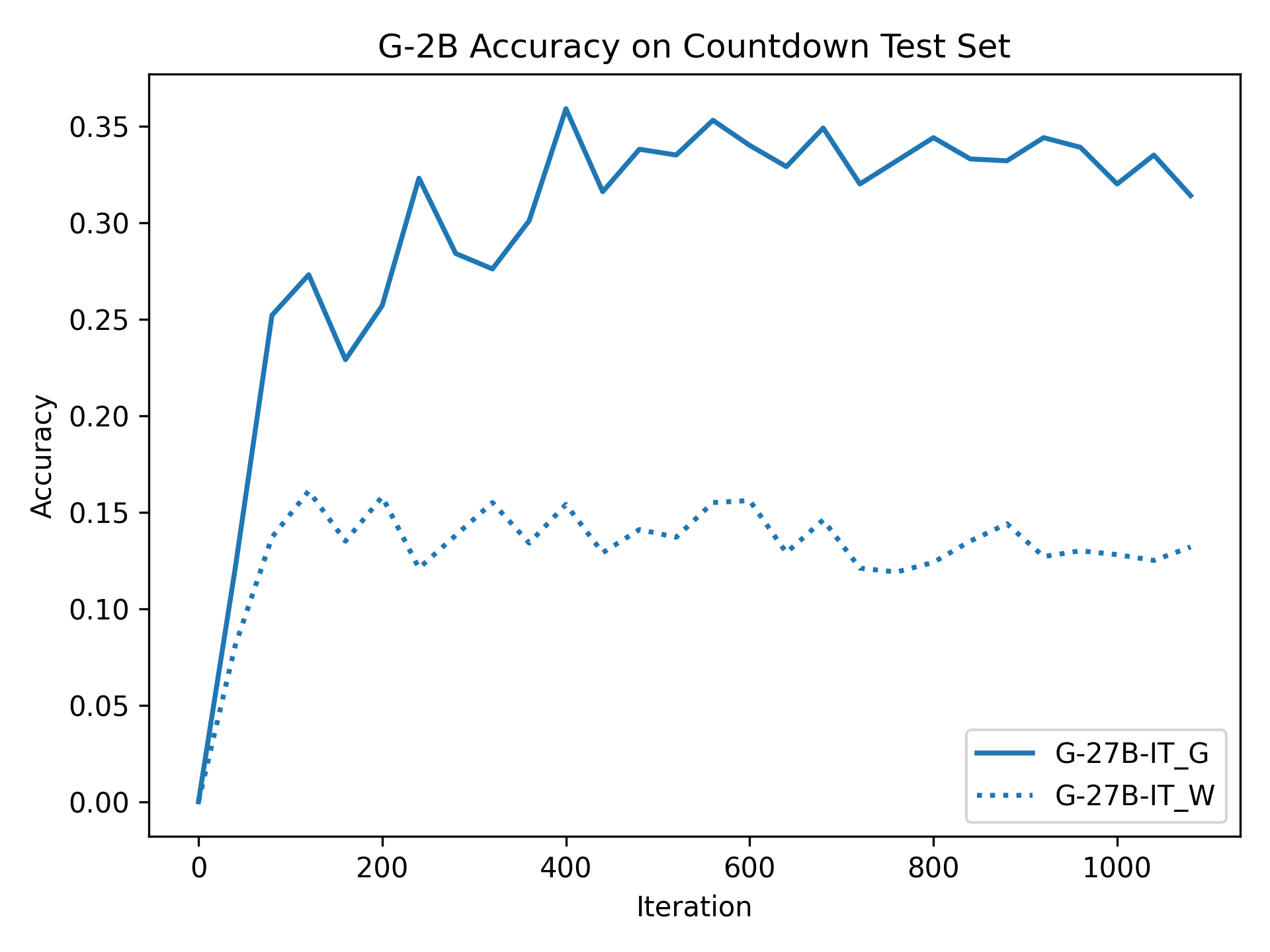
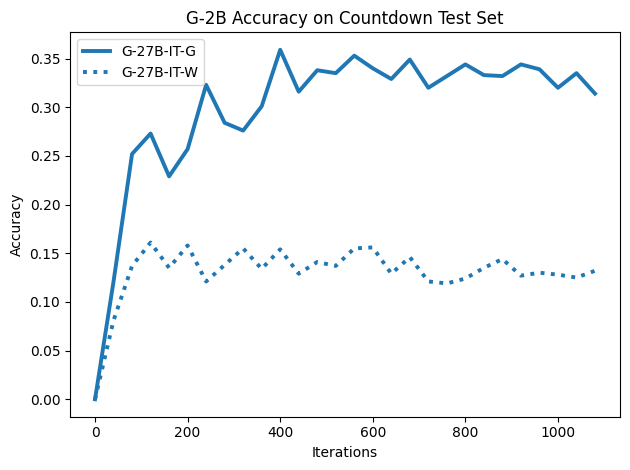
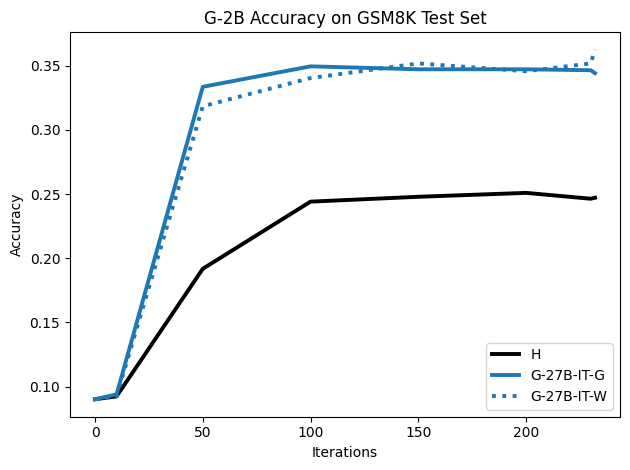
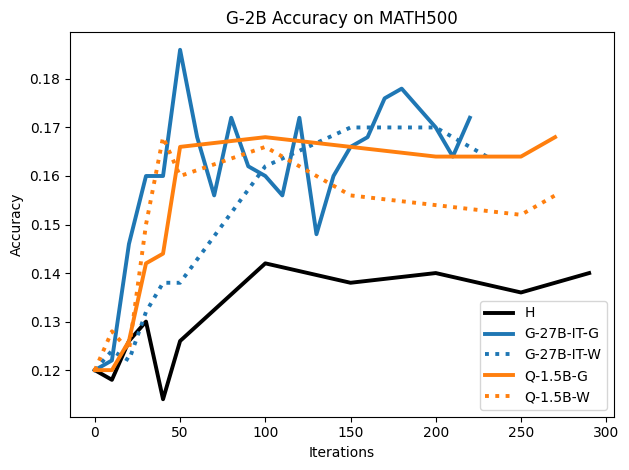
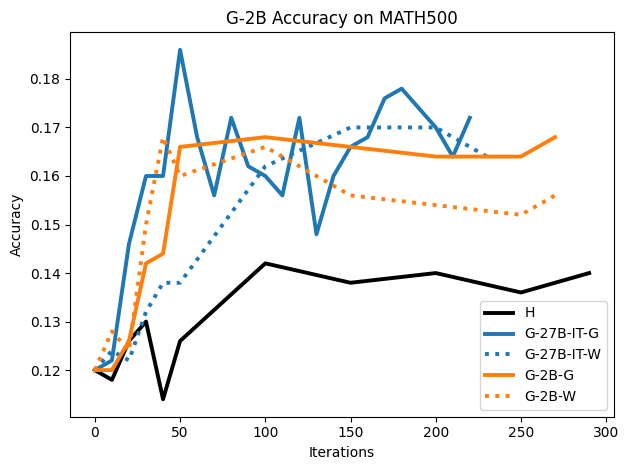
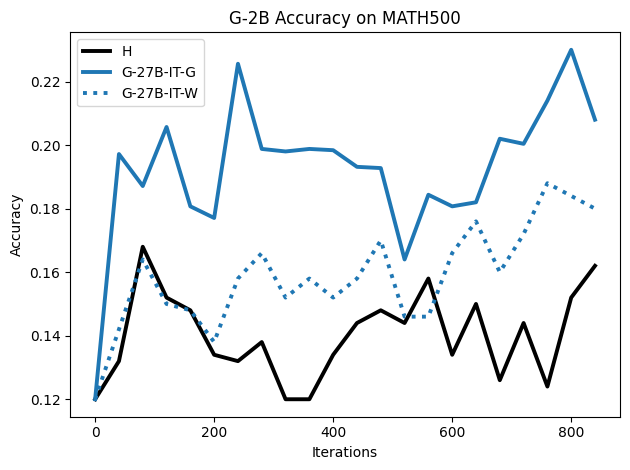
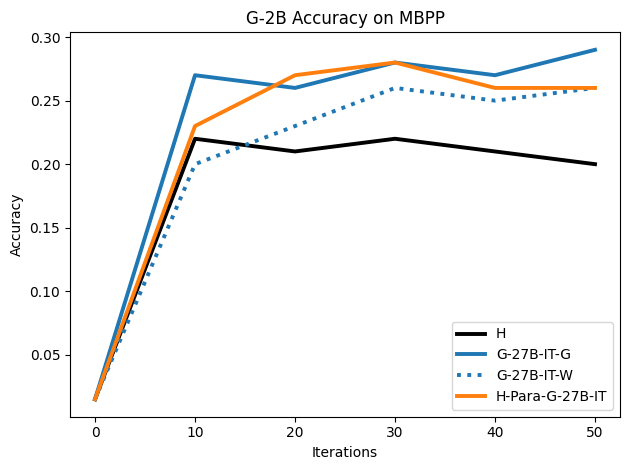
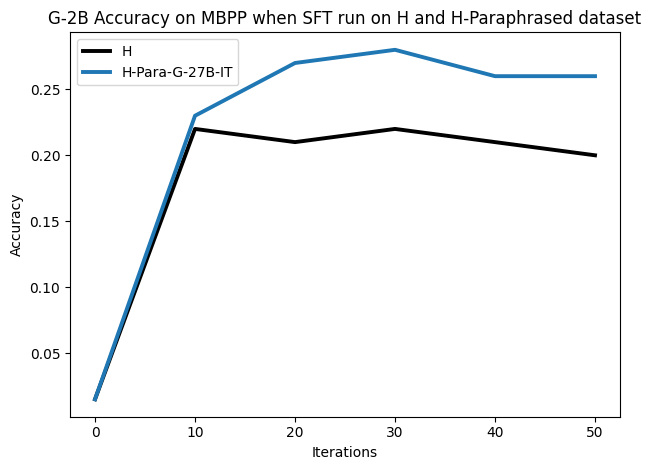
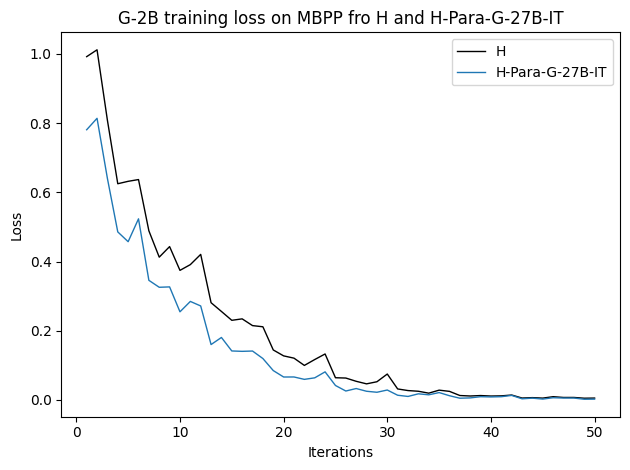
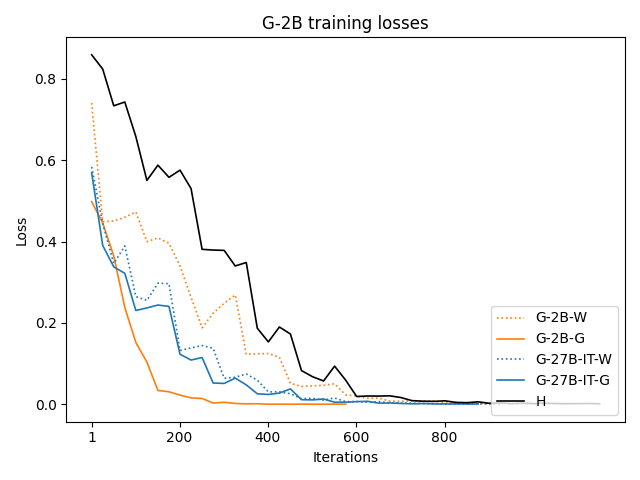
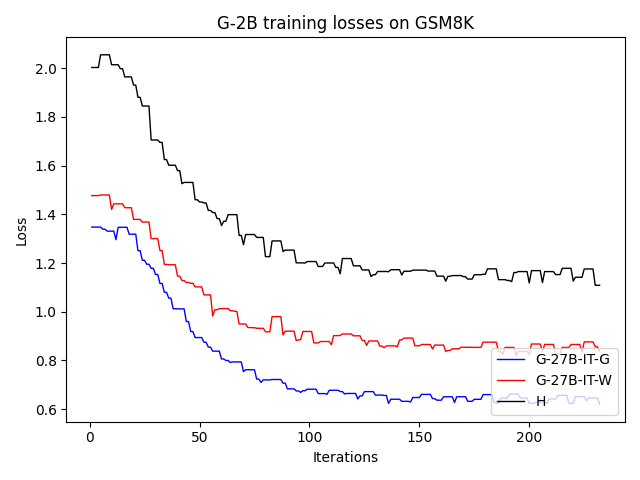
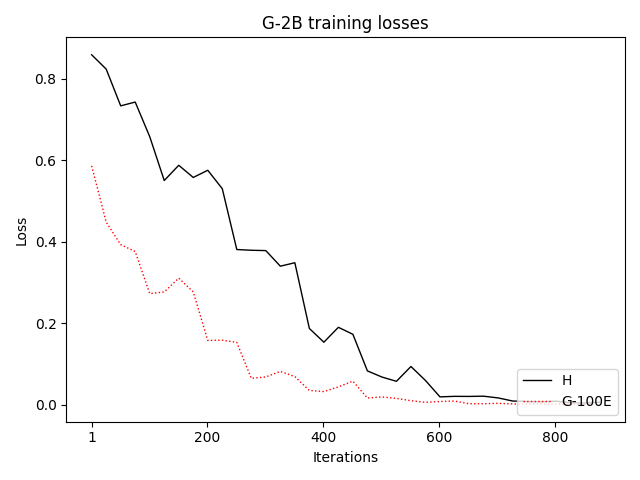
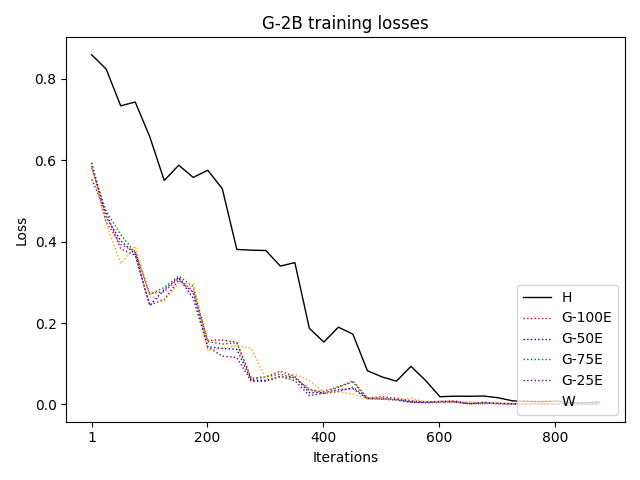
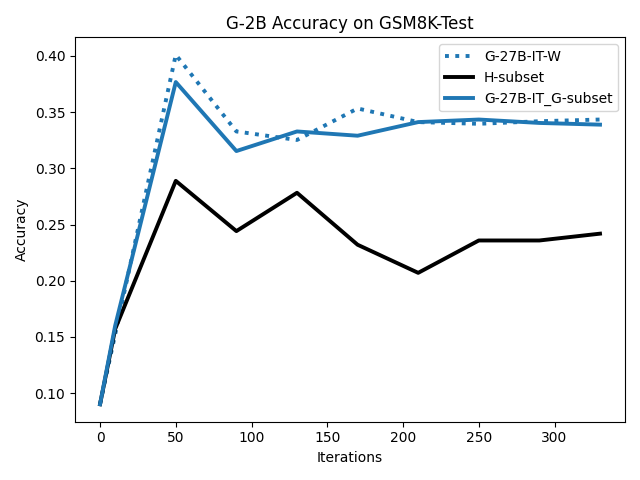
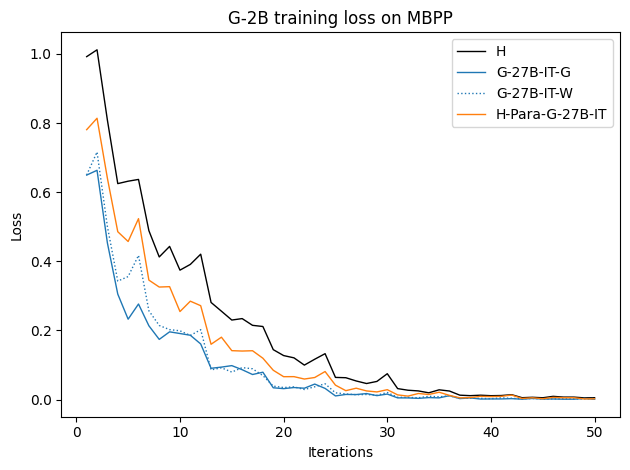
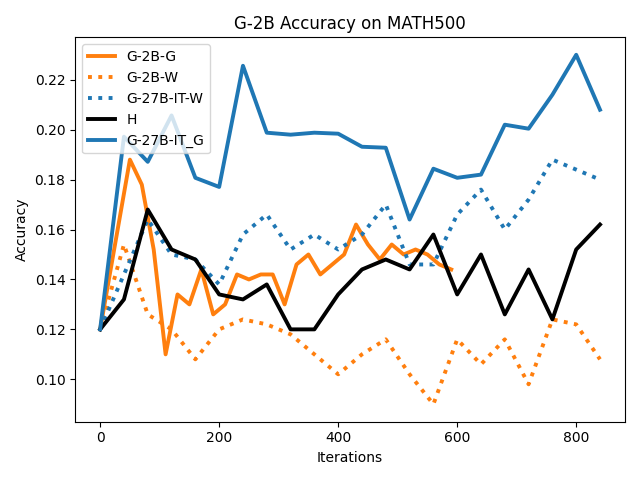
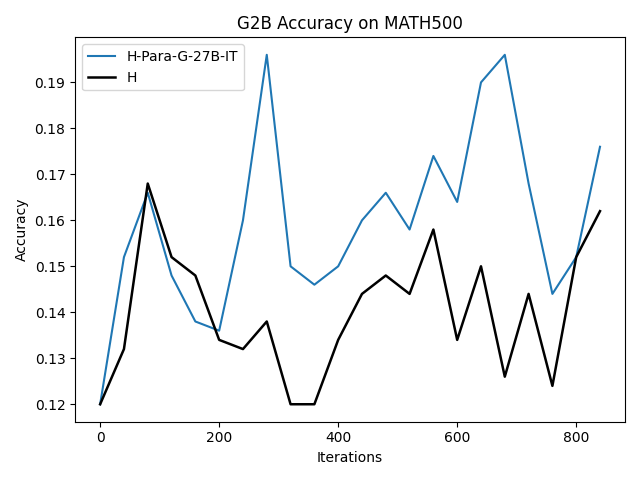
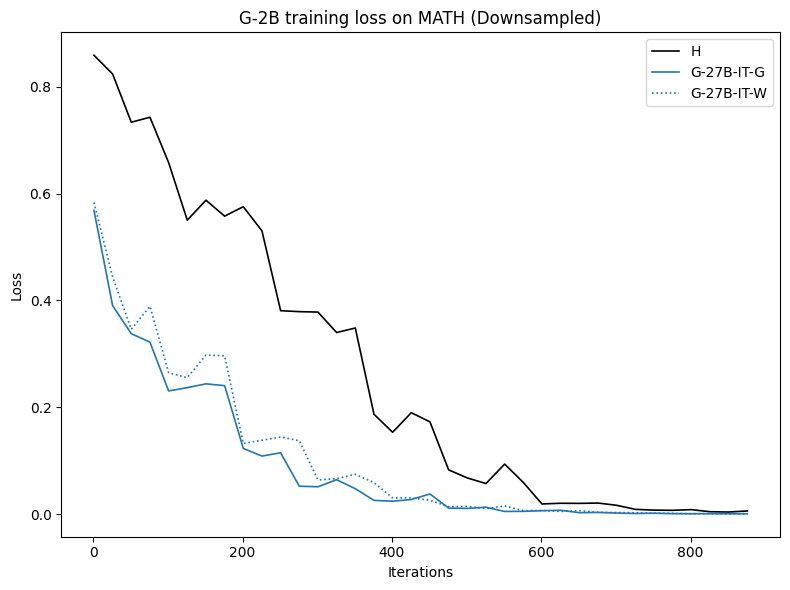
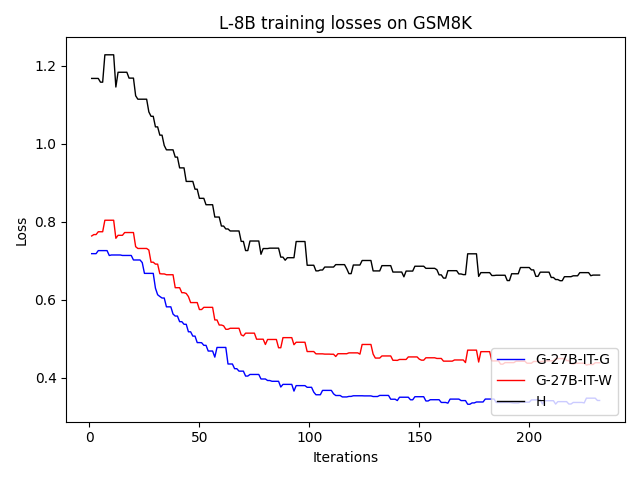
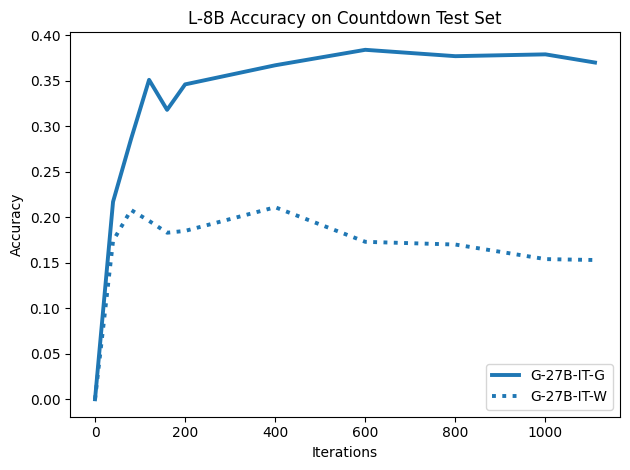
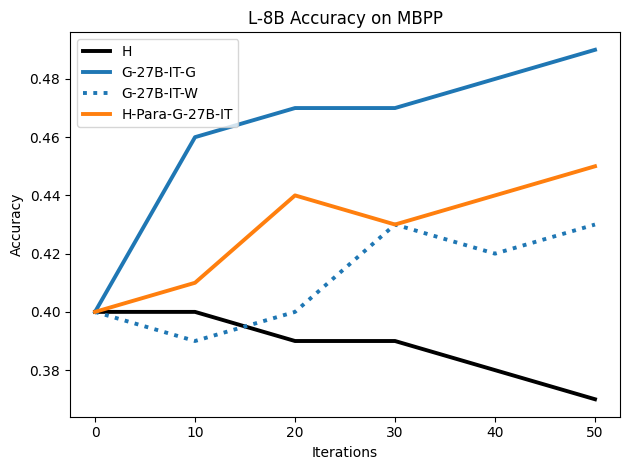
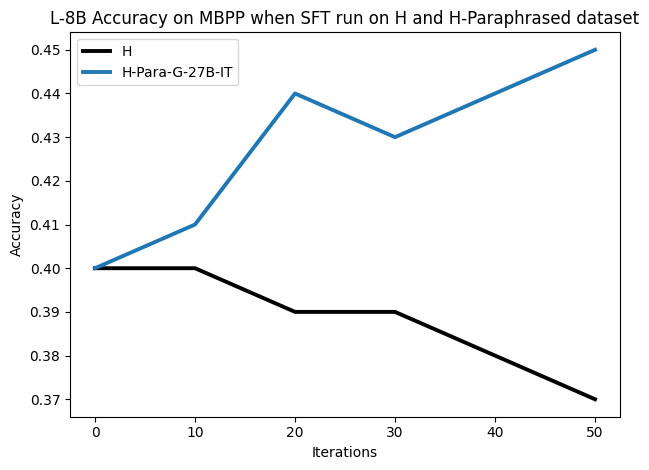
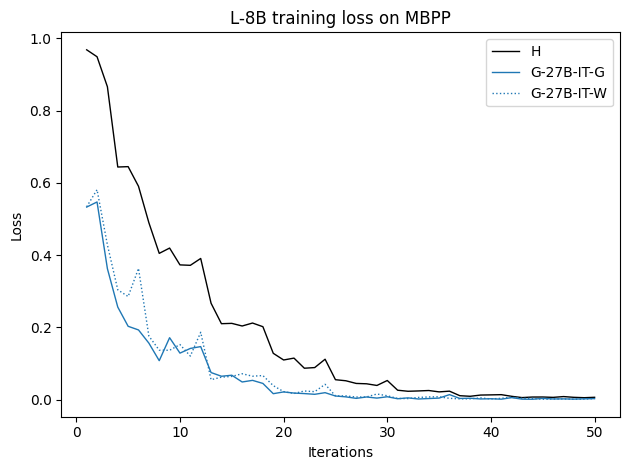
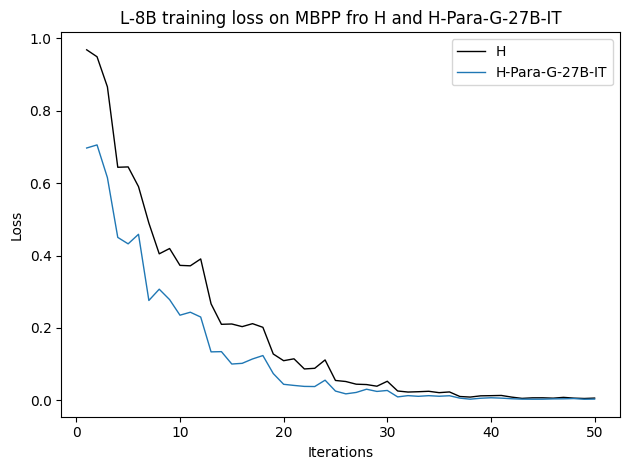
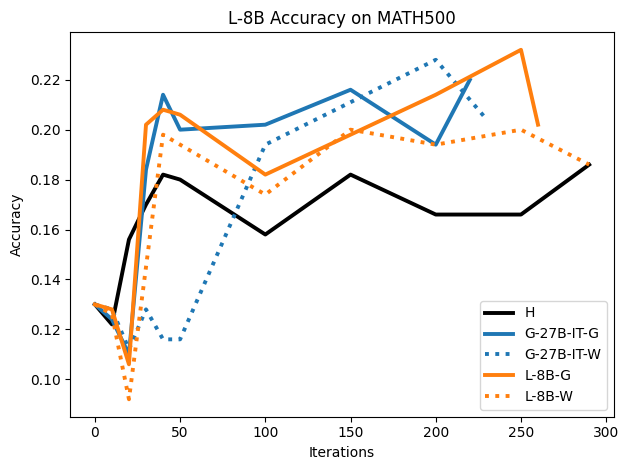
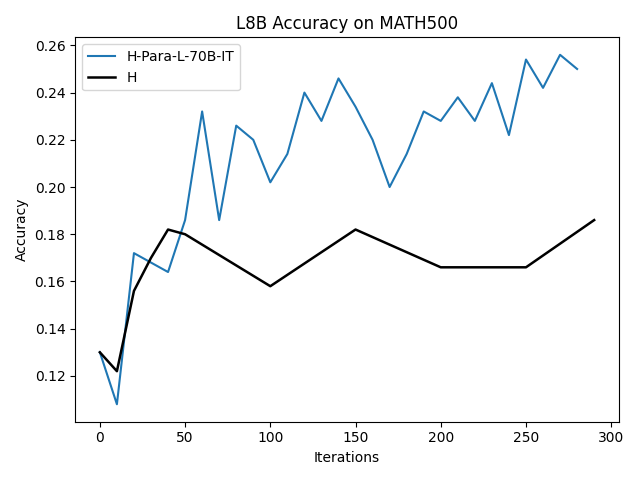
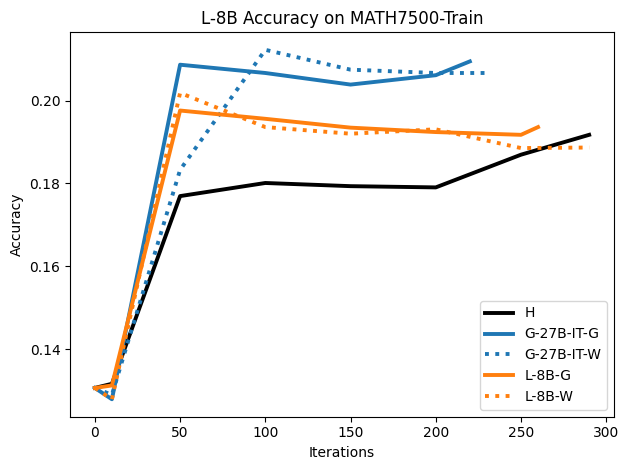
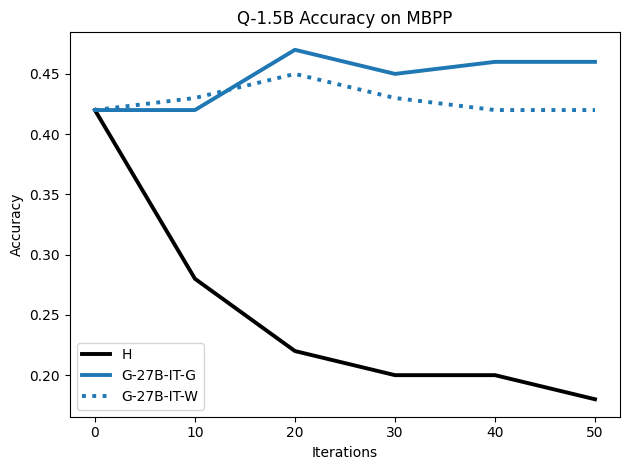
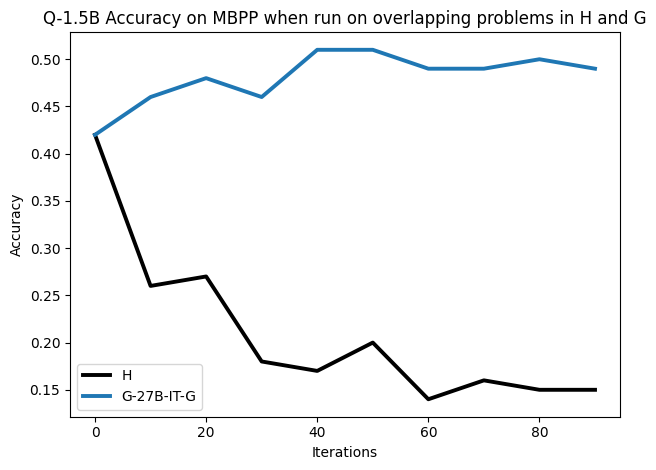
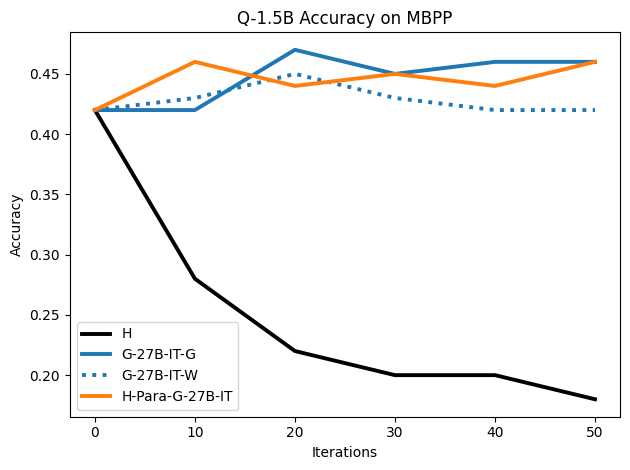
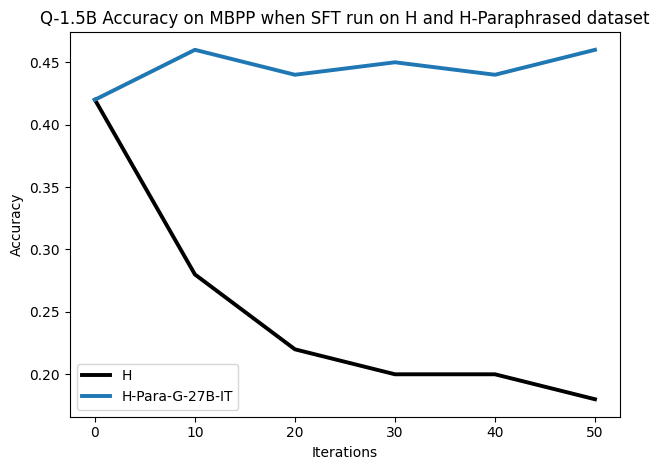
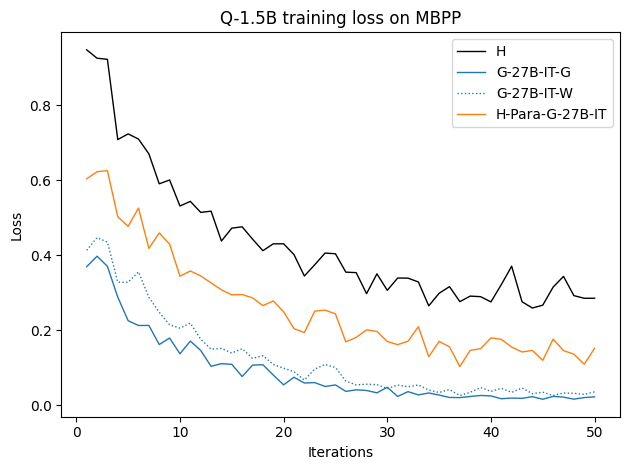
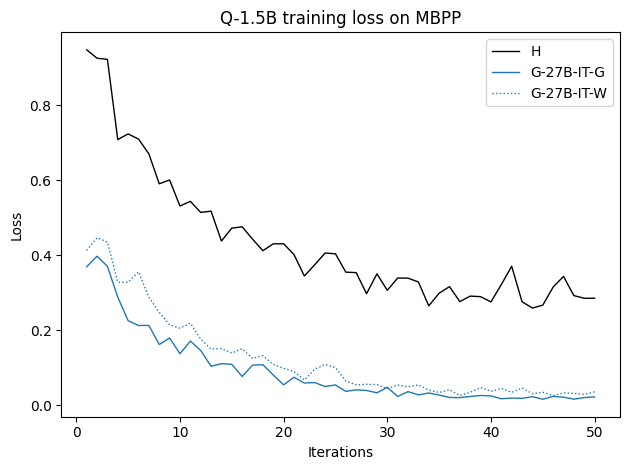
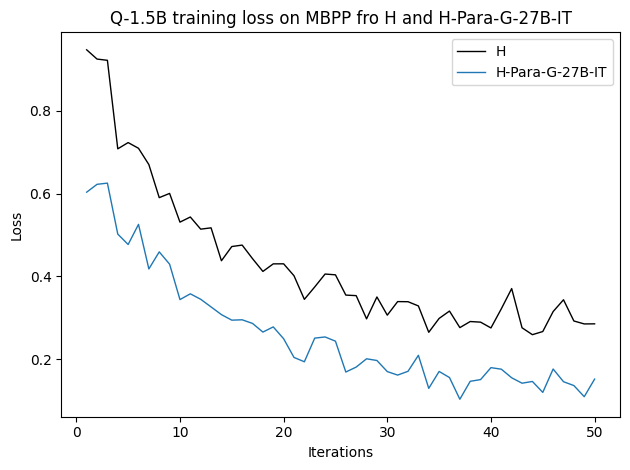
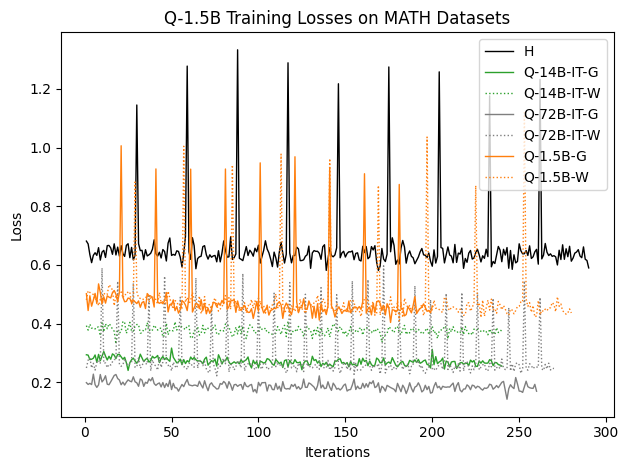
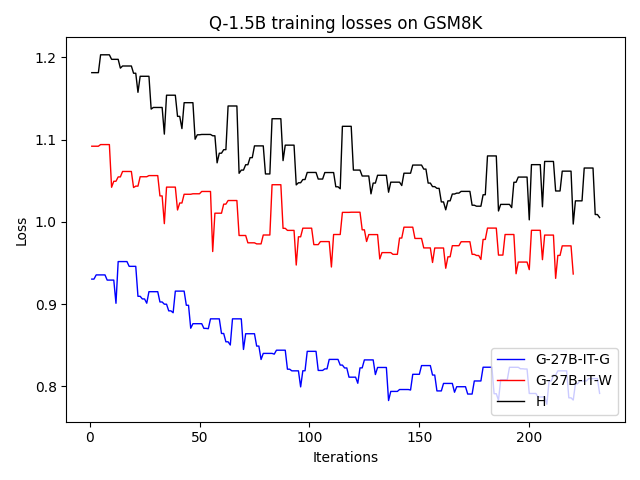
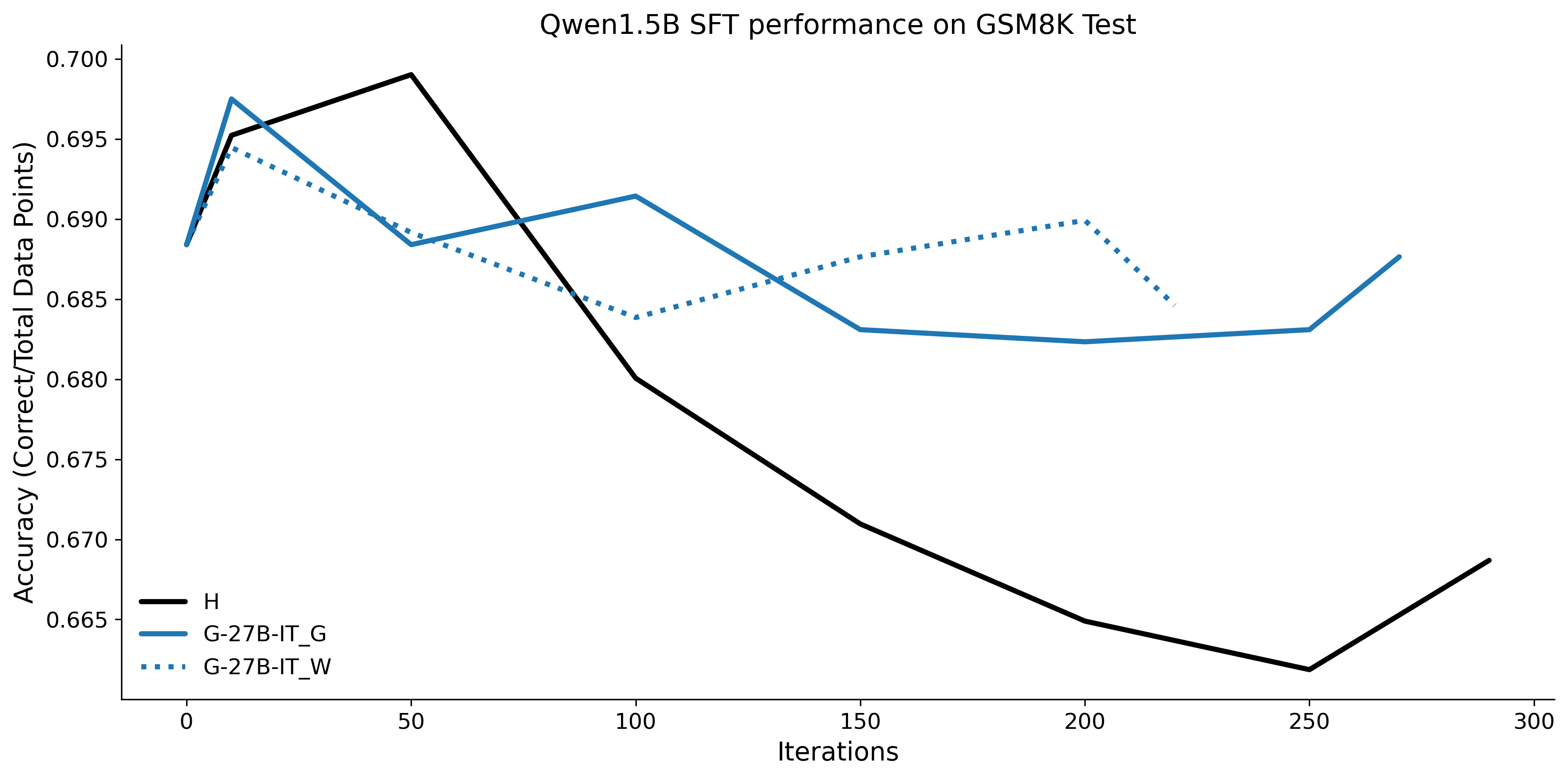
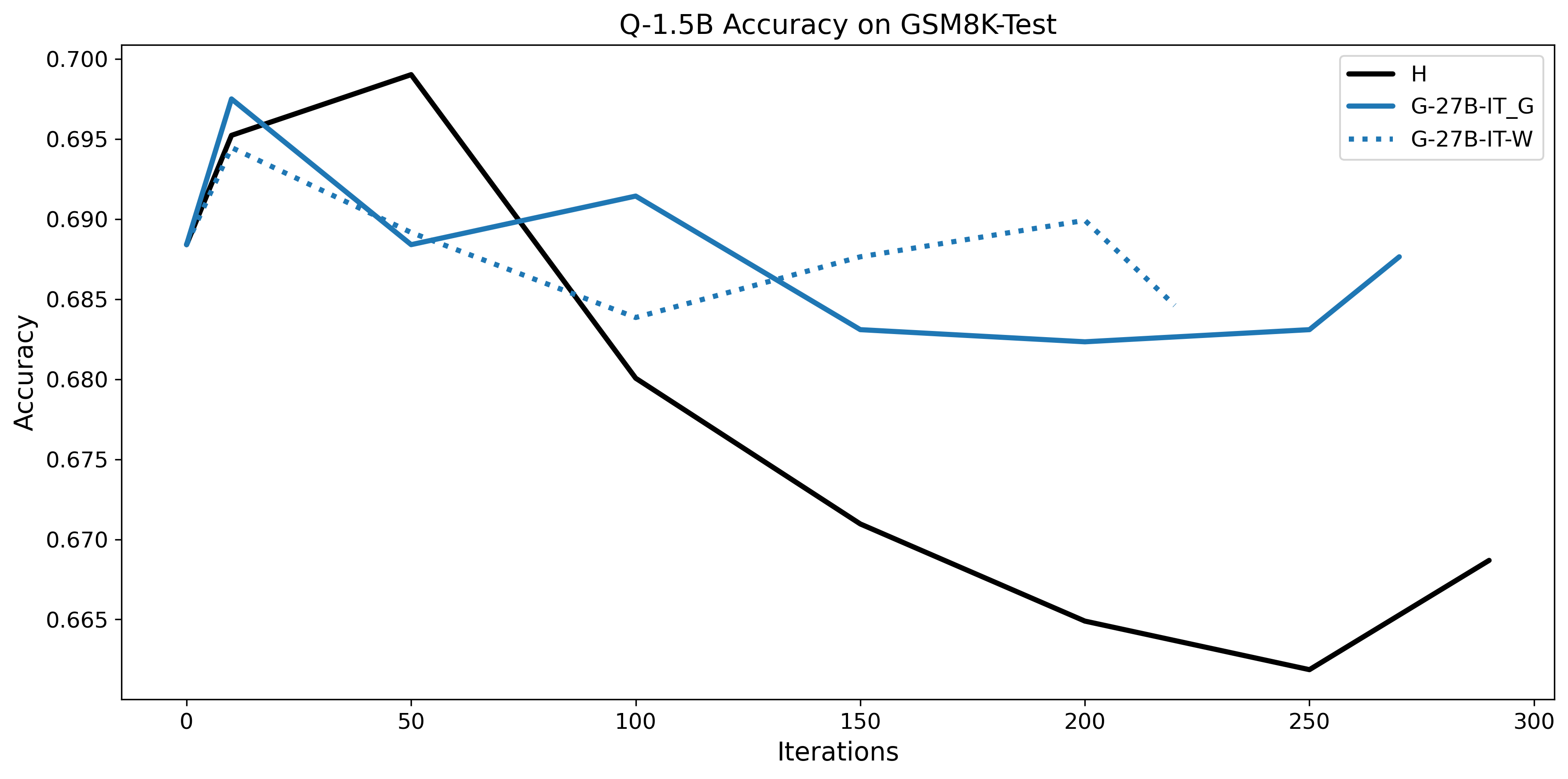
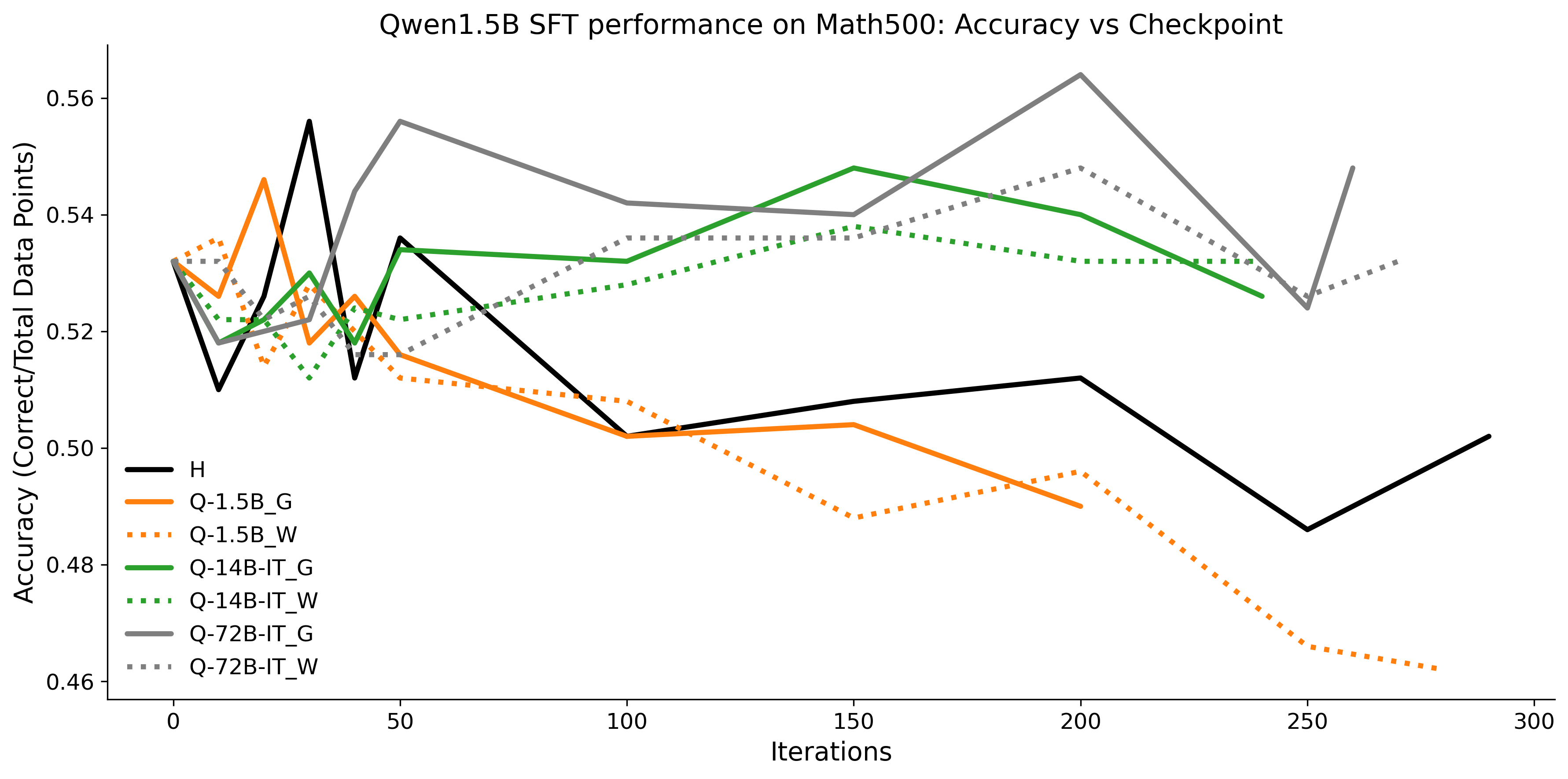
논문에서는 두 가지 주요 가설을 제시합니다: 첫째, 합성 데이터의 분포가 언어 모델 자체의 분포와 더 가깝기 때문에 학습이 용이하다는 점입니다. 이를 검증하기 위해 인간 주석 추적을 문장 변환하여 분포를 모델의 분포에 더 가깝게 이동시키고 성능 향상을 확인합니다.
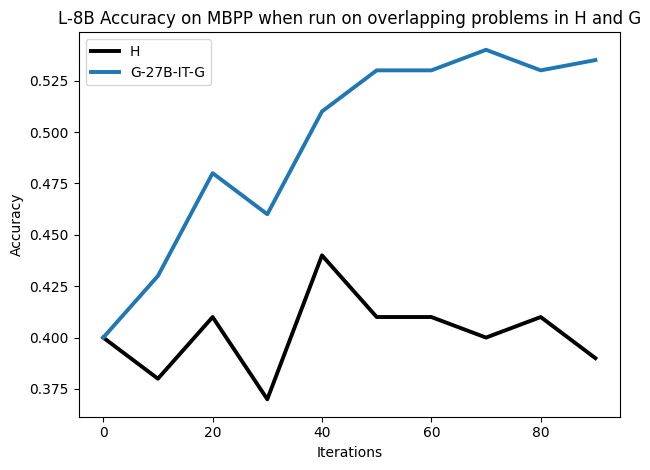
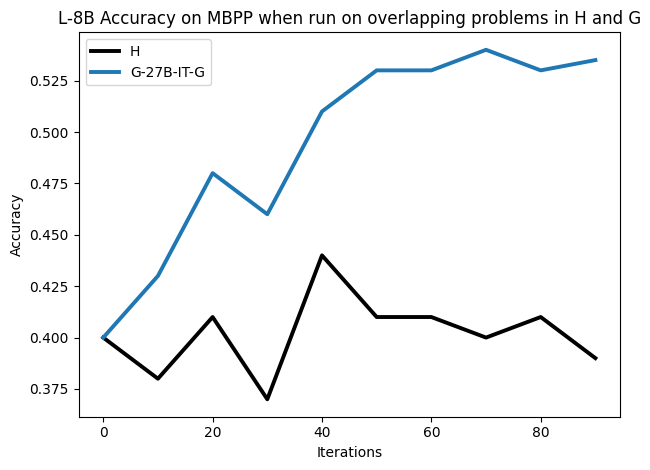
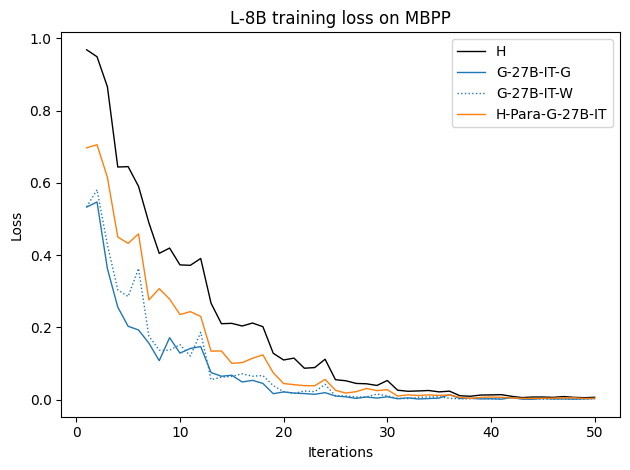
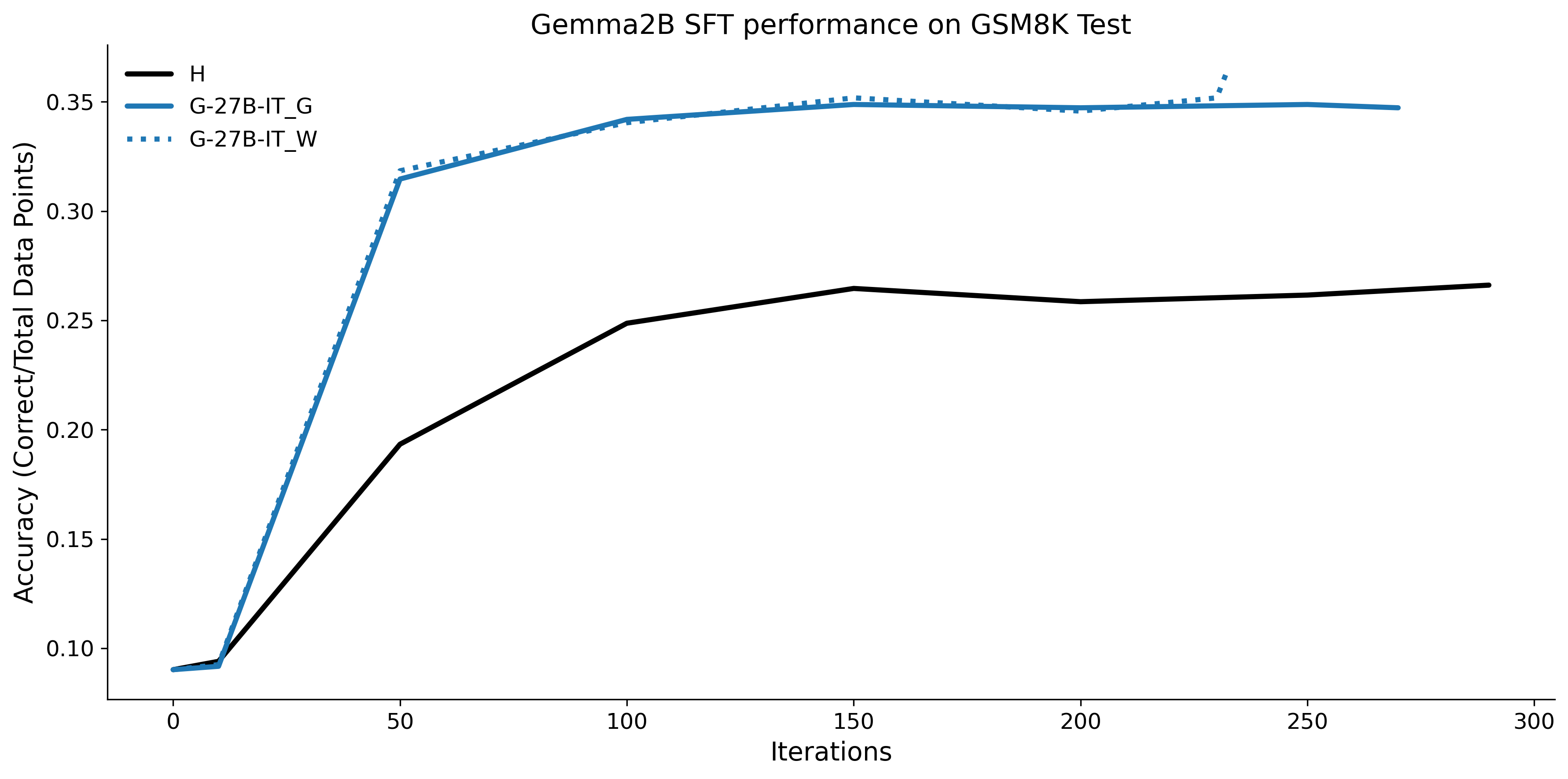
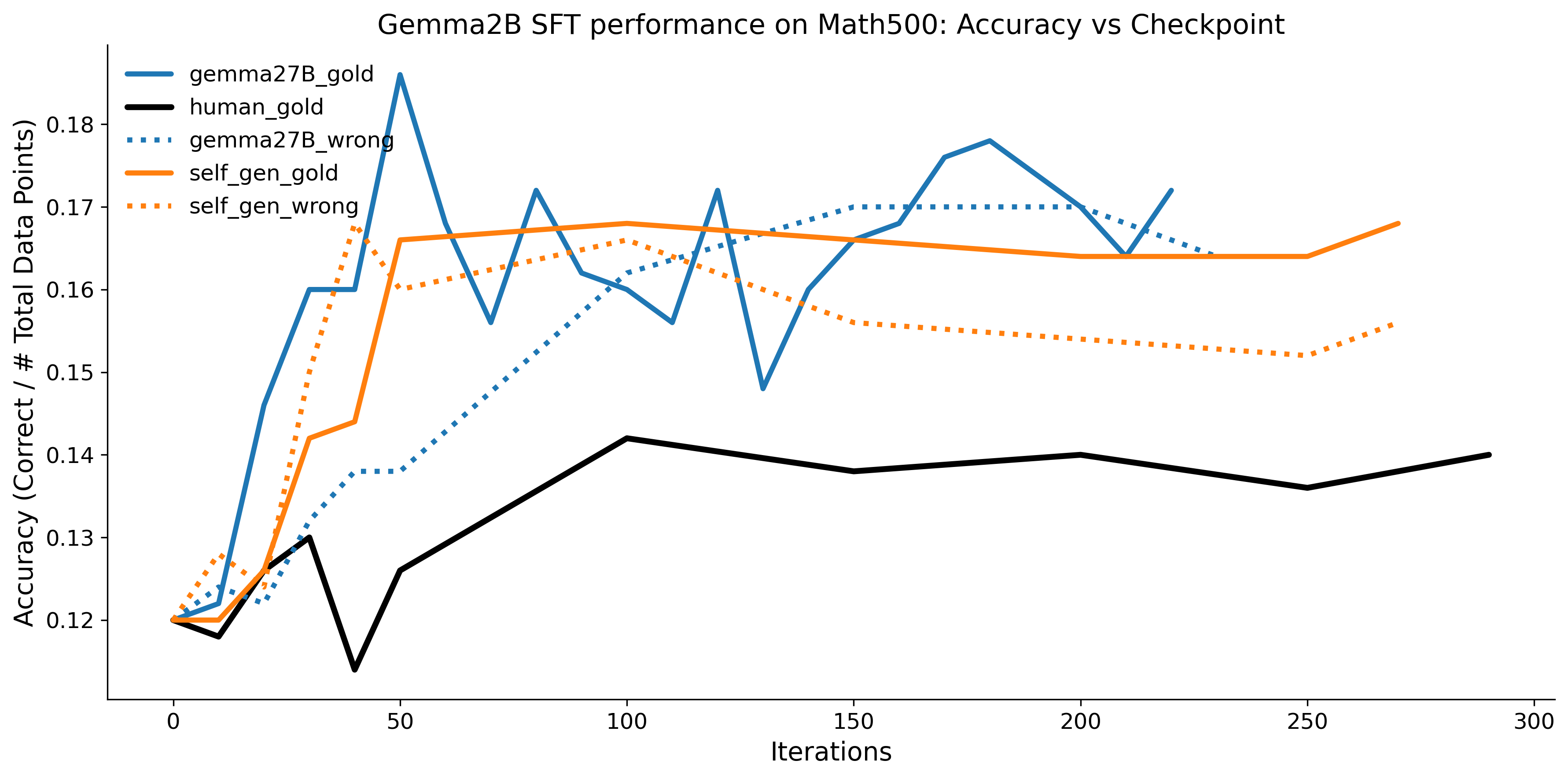
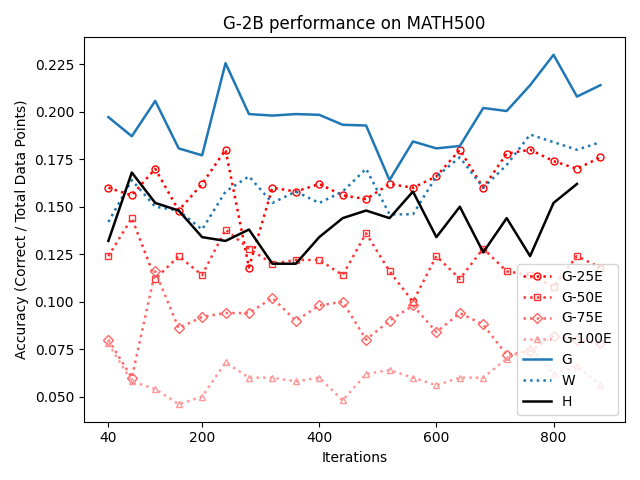
둘째, ‘잘못된’ CoT 추적이 종종 부분적으로 잘못되었지만 유효한 사고 단계를 포함하고 있어 모델이 이를 통해 배울 수 있다는 점입니다. 이를 검증하기 위해 점점 더 잘못된 CoT 추적을 도입하고 모델의 견디는 능력을 연구합니다.
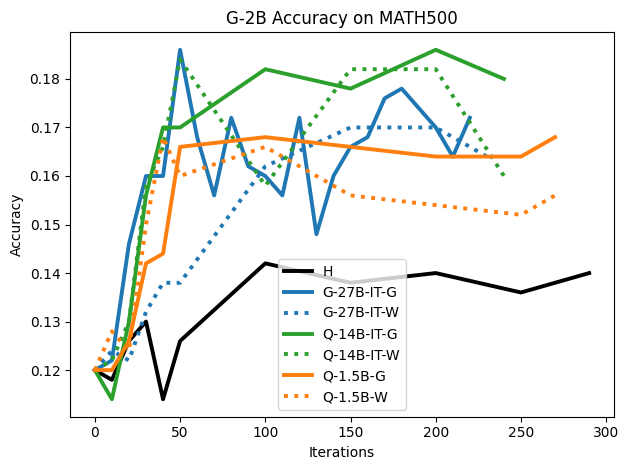
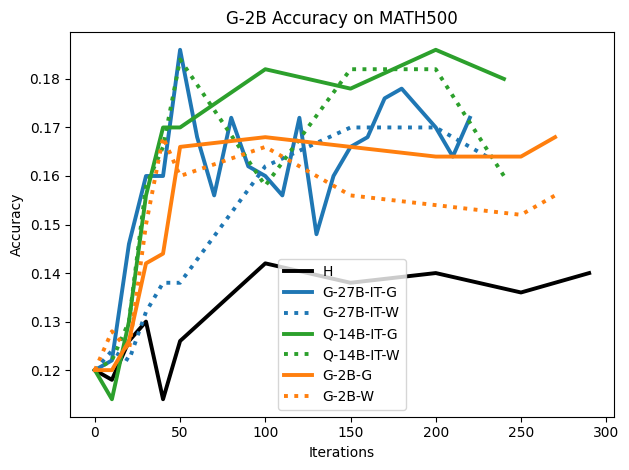
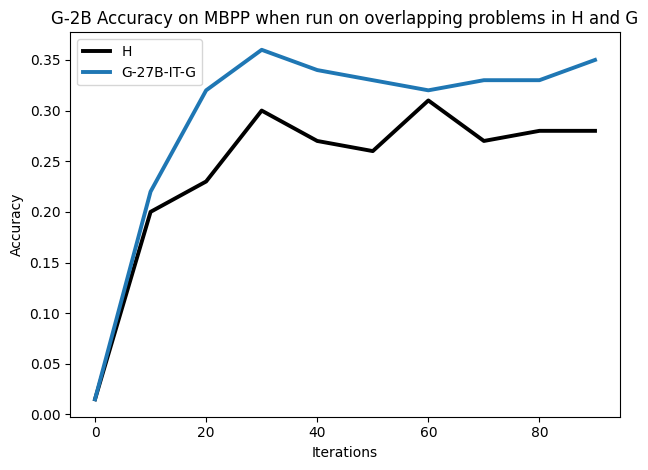
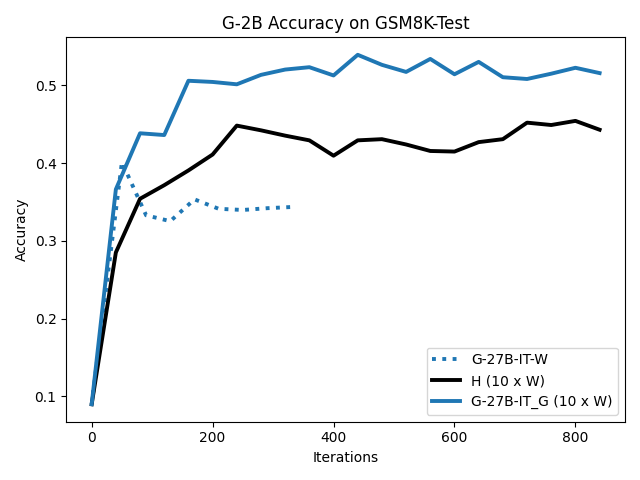
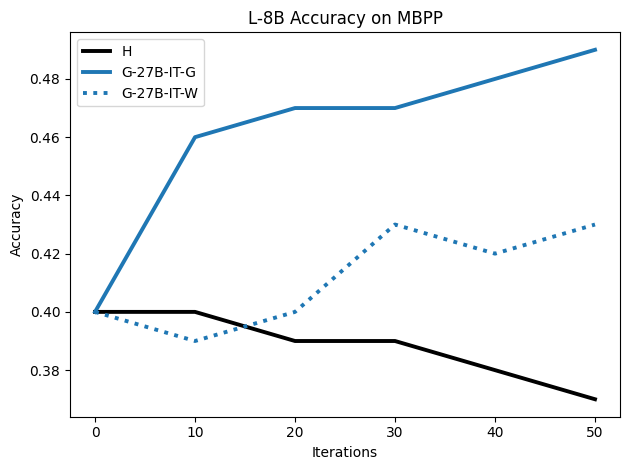
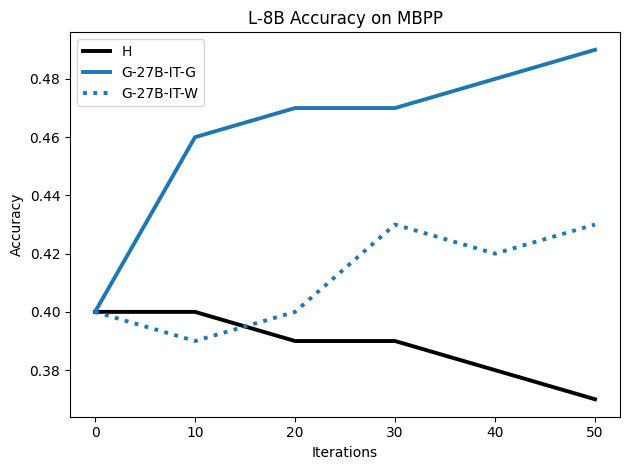
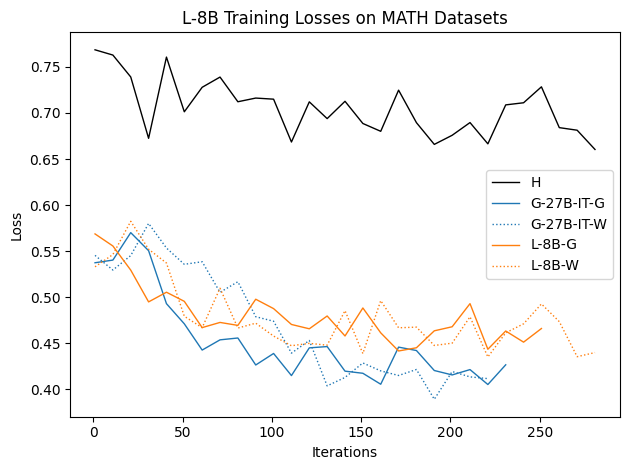
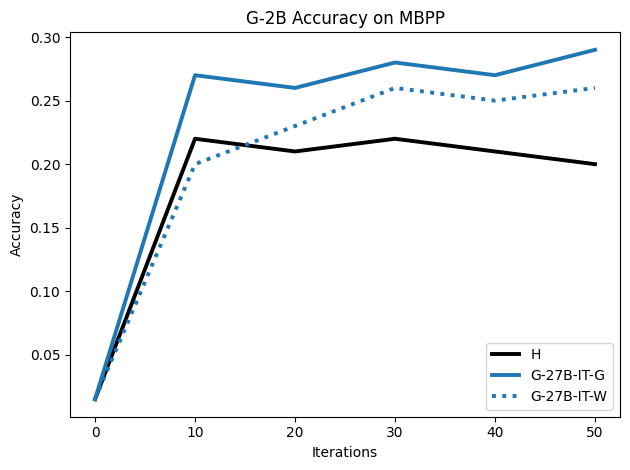
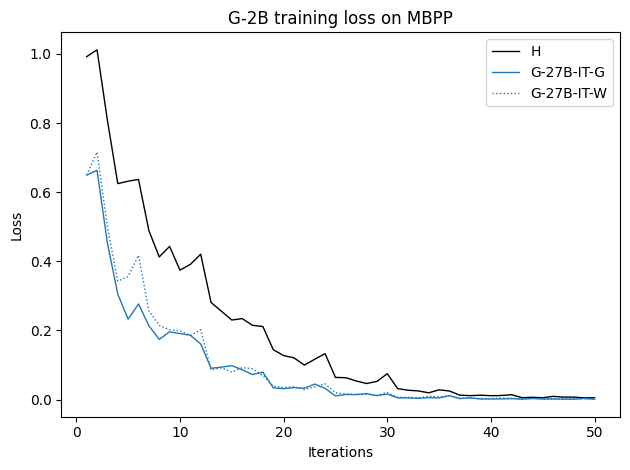
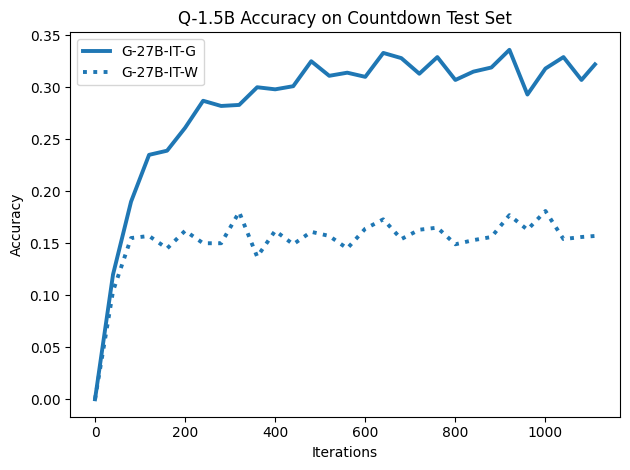
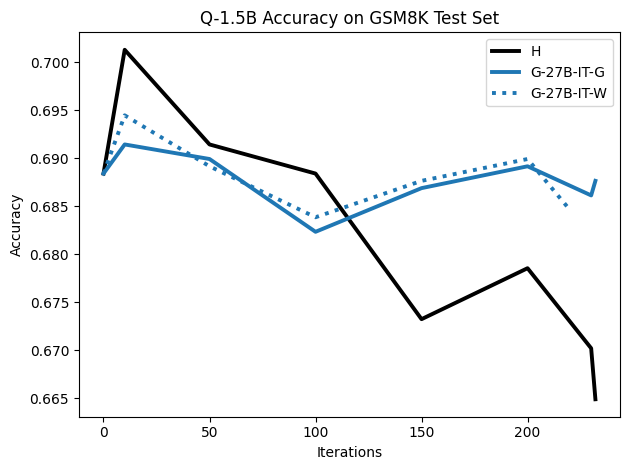
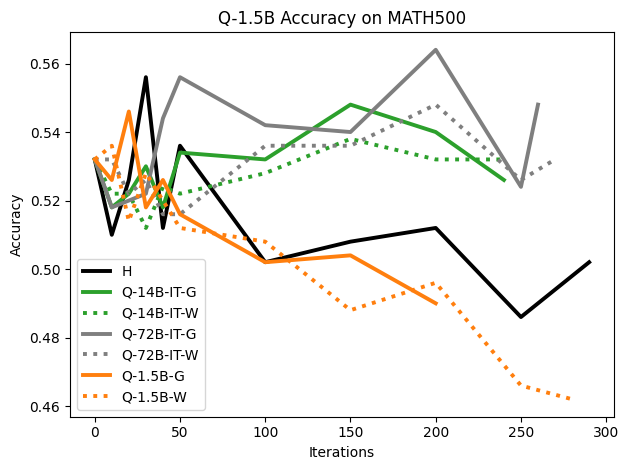
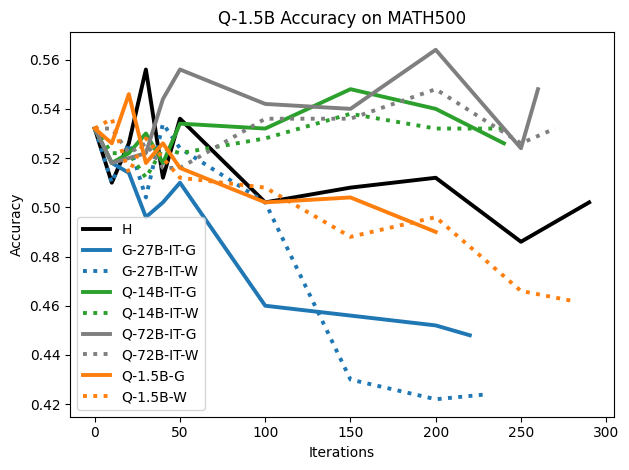
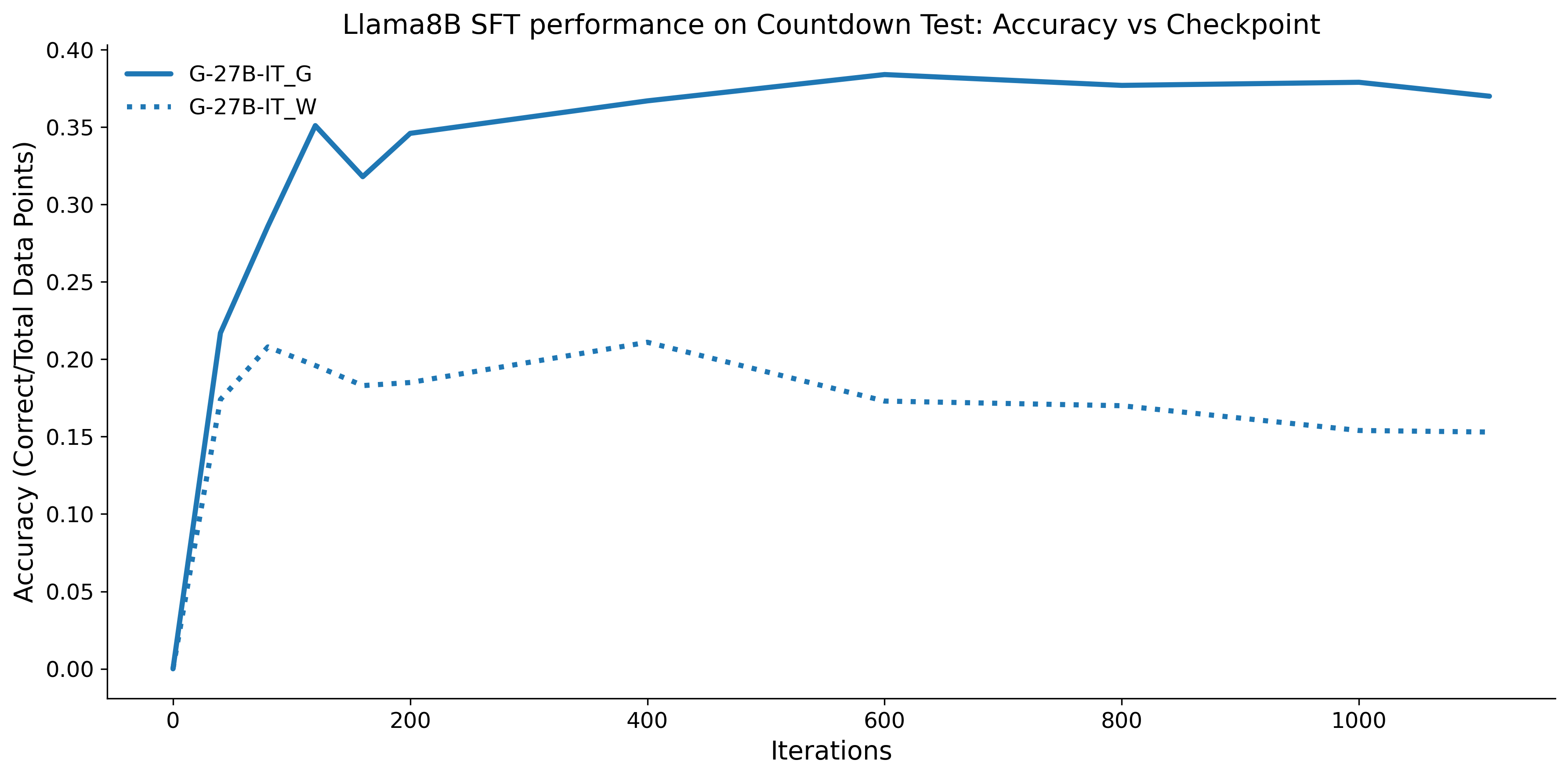
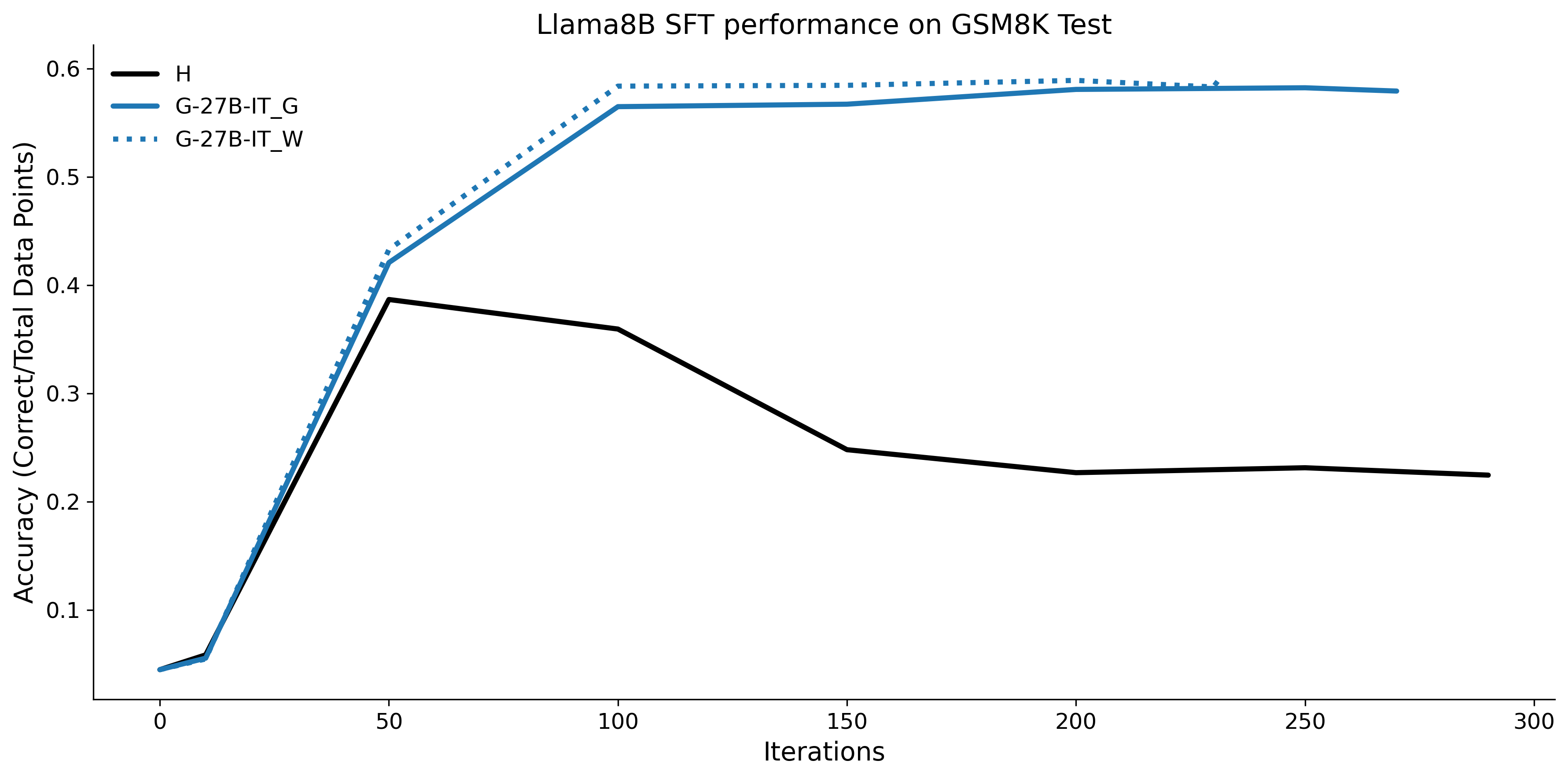
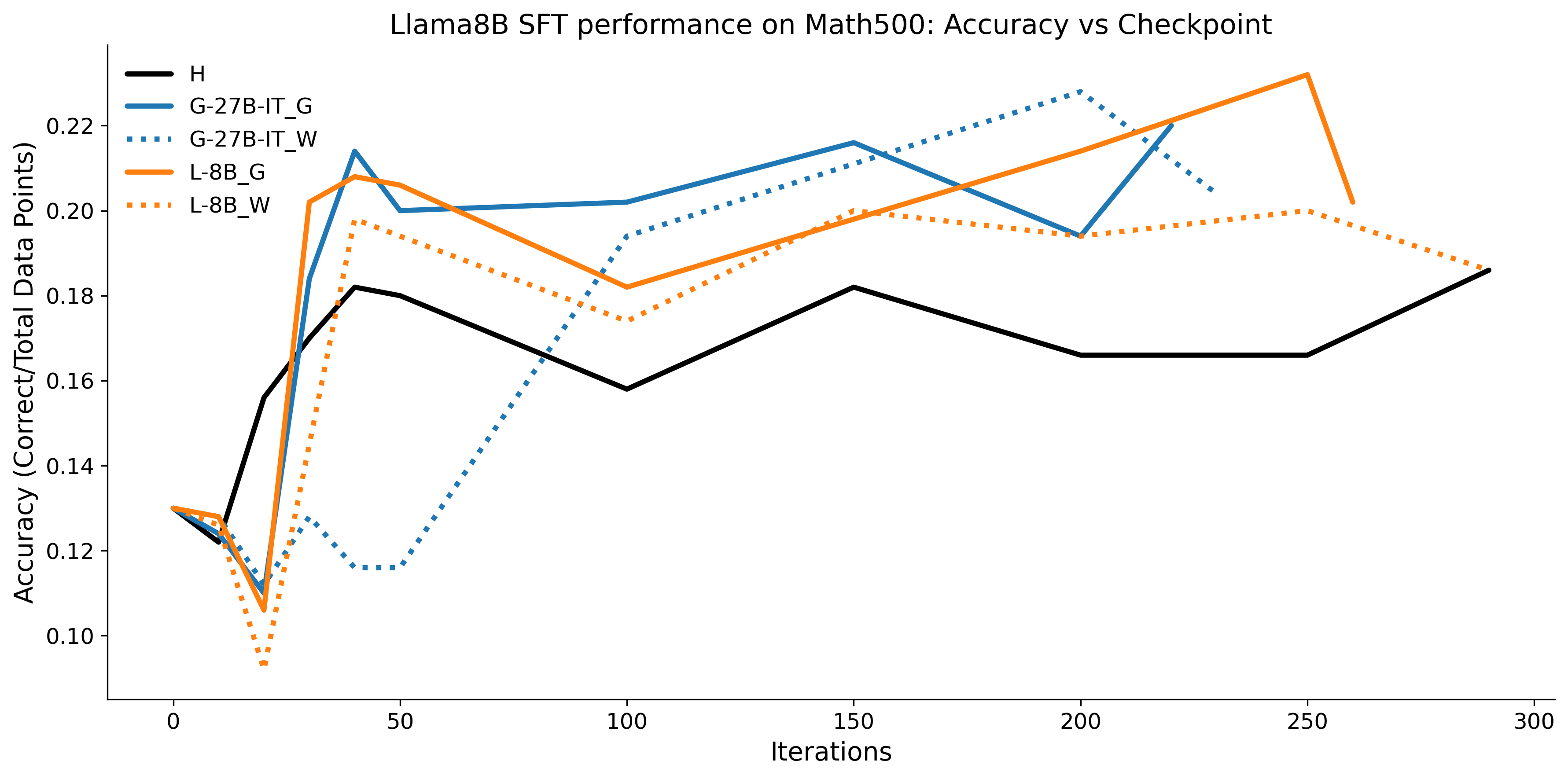
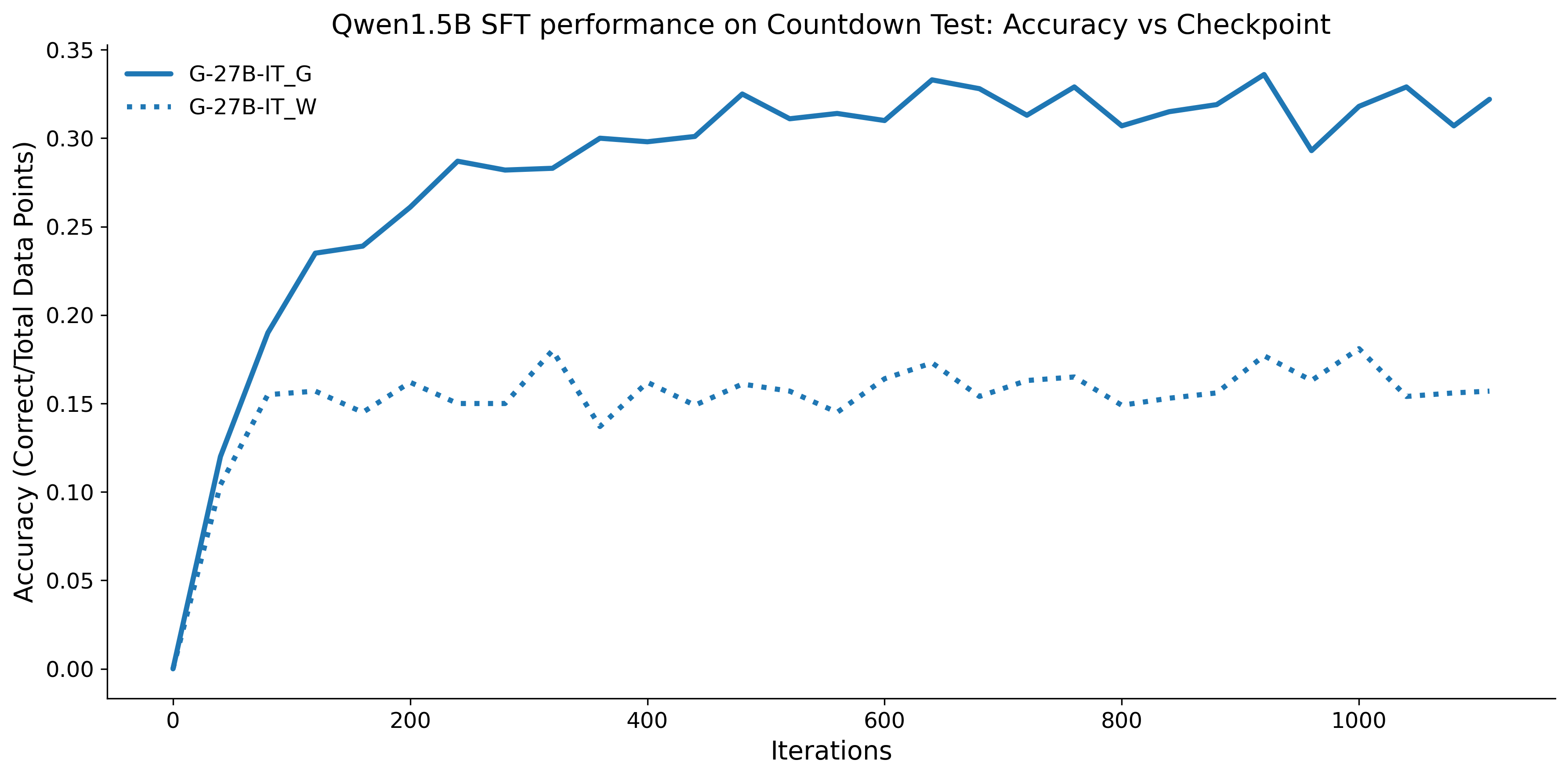
이 논문은 다양한 언어 모델(Qwen, Llama, Gemma)과 여러 크기(1.5B에서 9B 사이)를 사용하여 MATH, GSM8K, Countdown 및 MBPP 데이터셋을 통해 이 발견을 여러 추론 영역(수학, 알고리즘적 사고, 코드 생성 등)에 걸쳐 보여줍니다.
결과적으로 논문은 언어 모델의 성능 향상을 위한 합성 데이터셋의 중요성을 강조하며, 정확한 최종 답안이 항상 신뢰할 수 있는 추론 과정을 나타내는 지표가 아님을 보여줍니다. 이 연구는 언어 모델의 학습 방법에 대한 새로운 이해를 제공하고, 향후 연구에서 더 나은 성능을 위한 데이터셋 구성 전략을 제시합니다.
📄 논문 본문 발췌 (Excerpt)
📸 추가 이미지 갤러리