정확성을 넘어: 체스 평가에서 대형 언어 모델의 기하학적 안정성 분석
📝 원문 정보
- Title: Beyond Accuracy: A Geometric Stability Analysis of Large Language Models in Chess Evaluation
- ArXiv ID: 2512.15033
- 발행일: 2025-12-17
- 저자: Xidan Song, Weiqi Wang, Ruifeng Cao, Qingya Hu
📝 초록 (Abstract)
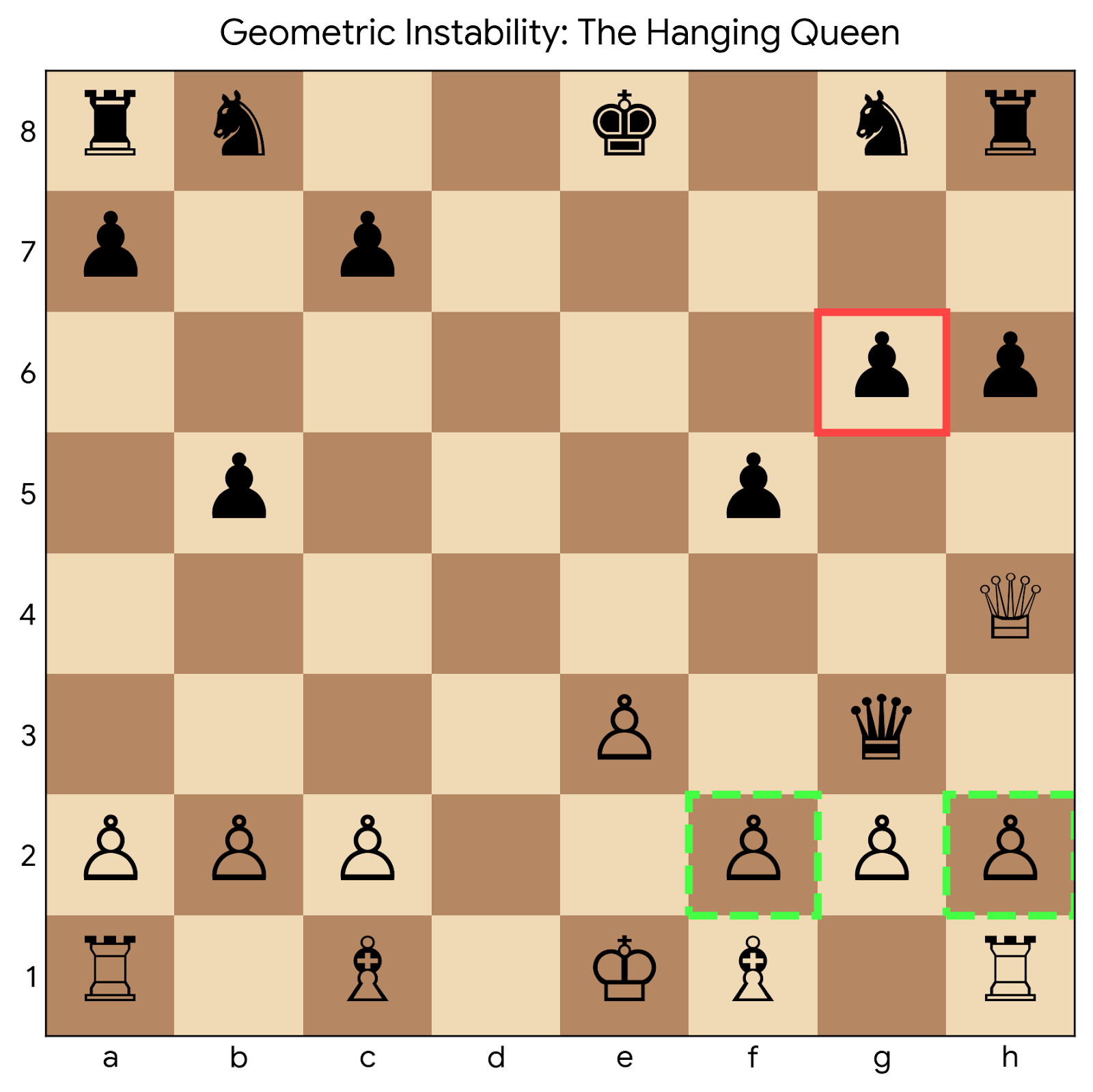
대형 언어 모델(LLM)의 복합 추론 능력을 평가할 때는 보통 Stockfish와 같은 강력한 체스 엔진을 기준으로 정확도를 측정한다. 그러나 높은 스칼라 정확도가 실제 개념적 이해를 보장하지는 않는다. 본 논문은 기존 정확도 지표가 모델이 기하학적 추론을 수행하는지, 아니면 정형화된 보드 상태를 암기하는지 구분하지 못한다는 점을 지적한다. 이를 해결하기 위해 보드 회전, 대칭, 색상 반전, 포맷 변환 등 불변 변환 하에서 모델의 일관성을 검증하는 ‘기하학적 안정성 프레임워크’를 제안한다. 약 3,000개의 포지션을 이용해 GPT‑5.1, Claude Sonnet 4.5, Kimi K2 Turbo 등 6개 최신 LLM을 비교 분석한 결과, GPT‑5.1은 표준 포지션에서 평균 절대 오차가 362 cp 정도로 거의 최적에 가까운 정확도를 보였지만, 회전 변환에서는 오류가 600 % 이상 급증해 2,500 cp를 초과했다. 이는 모델이 패턴 매칭에 의존하고 추상적 공간 논리를 부족하게 사용한다는 증거이다. 반면 Claude Sonnet 4.5와 Kimi K2 Turbo는 모든 변환 축에서 높은 일관성을 유지하며 정확도와 안정성 모두에서 우수한 성능을 보였다.💡 논문 핵심 해설 (Deep Analysis)
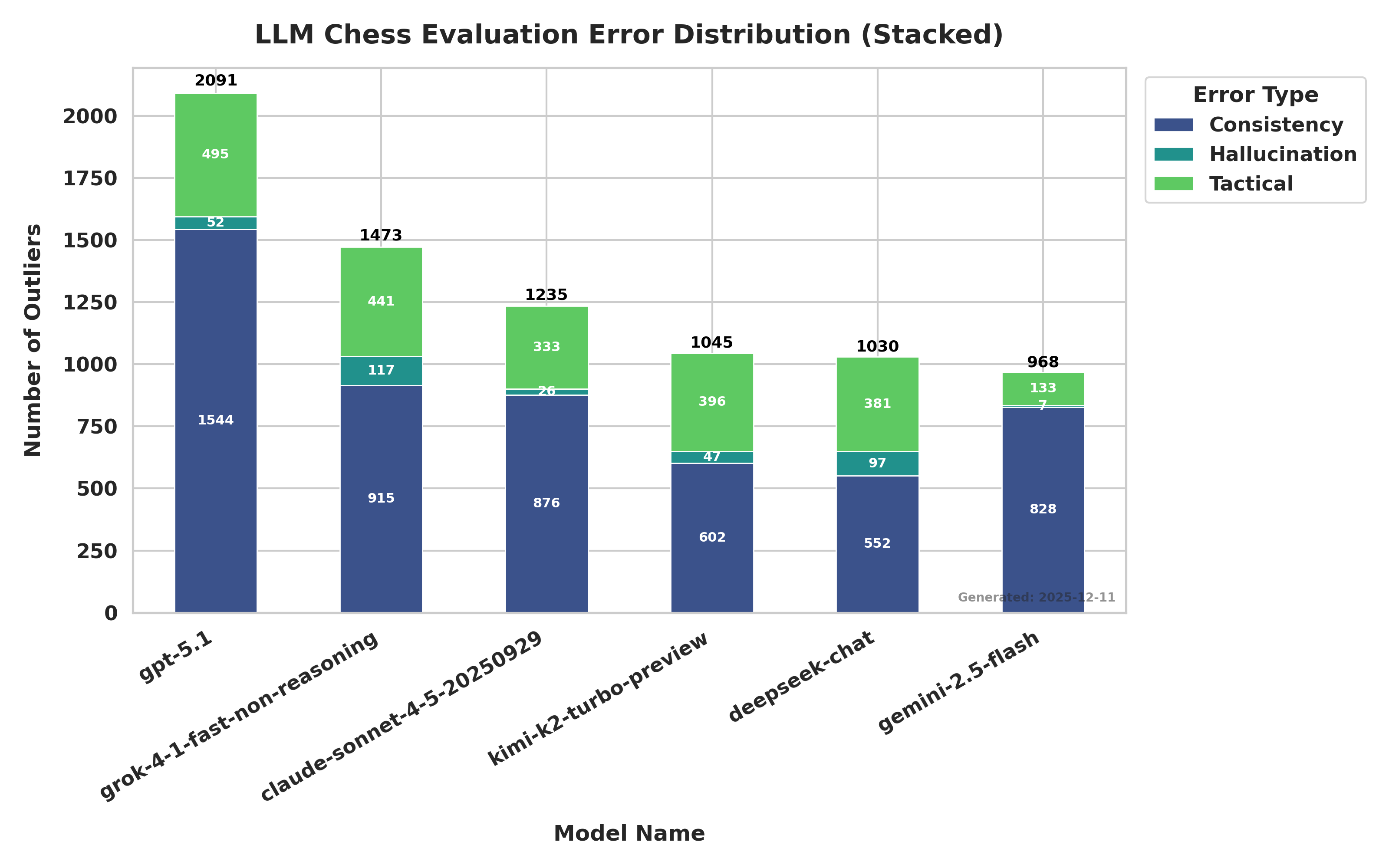
실험 결과를 보면, GPT‑5.1은 표준 포지션에서는 평균 절대 오차(MAE) 362 cp라는 거의 인간 수준의 정확도를 기록했지만, 보드를 90도 회전시켰을 때 오차가 2,500 cp를 넘어 600 % 이상 급증한다. 이는 모델이 “e4”와 같은 특정 기보를 기억하고 있을 뿐, “e4”가 보드의 어느 위치에 있든 동일한 전략을 적용한다는 추상적 규칙을 내재하고 있지 않음을 의미한다. 반면 Claude Sonnet 4.5와 Kimi K2 Turbo는 회전, 좌우 대칭, 색상 반전, FEN↔ASCII 변환 등 모든 변환에서 오차 증가폭이 미미했고, 전체 MAE가 400 cp 이하로 유지되었다. 이는 두 모델이 체스 보드의 기하학적 구조를 보다 깊이 이해하고, 변환 불변성을 학습했음을 시사한다.
또한 논문은 ‘정확도‑안정성 역설(Accuracy‑Stability Paradox)’이라는 현상을 제시한다. 높은 정확도가 반드시 모델의 일반화 능력이나 추론 능력을 보장하지 않으며, 오히려 변환에 대한 취약성은 모델이 표면적인 패턴 매칭에 의존하고 있음을 드러낸다. 따라서 LLM을 실제 복합 추론 도메인에 적용하려면, 정확도 외에도 변환 불변성, 논리적 일관성, 구조적 견고성을 평가하는 다차원 지표가 필요하다.
이 연구는 체스뿐 아니라 수학, 물리, 그래픽스 등 기하학적 불변성이 핵심인 다른 분야에도 적용 가능하다. 향후 연구에서는 변환 종류를 확대하고, 변환에 강인한 사전 학습 기법이나 구조적 프롬프트 설계 방안을 모색함으로써 LLM의 ‘추상적 사고’를 한 단계 끌어올릴 수 있을 것이다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리