제약 만족 문제를 위한 가이드형 이산 확산
📝 원문 정보
- Title: Guided Discrete Diffusion for Constraint Satisfaction Problems
- ArXiv ID: 2512.14765
- 발행일: 2025-12-16
- 저자: Justin Jung
📝 초록 (Abstract)
본 논문에서는 제약 만족 문제(CSP)를 해결하기 위해 이산 확산 모델에 가이드를 결합한 새로운 프레임워크를 제시한다. 제안된 방법은 연속적인 확산 과정에서 얻은 샘플을 이산 공간으로 매핑하고, 문제 특유의 제약을 만족하도록 유도하는 가이드 함수를 설계한다. 이를 위해 우리는 (i) 이산 변수에 대한 효율적인 전방 및 역방향 전이 확률을 정의하고, (ii) 제약 위반을 최소화하도록 설계된 라그랑지안 기반 가이드를 도입한다. 실험 결과, 그래프 색칠, 스도쿠, 그리고 N-퀸 문제와 같은 표준 CSP 벤치마크에서 기존 최첨단 방법들을 능가하는 성능을 보이며, 특히 높은 제약 밀도와 큰 변수 공간에서도 안정적인 수렴 특성을 나타낸다.💡 논문 핵심 해설 (Deep Analysis)
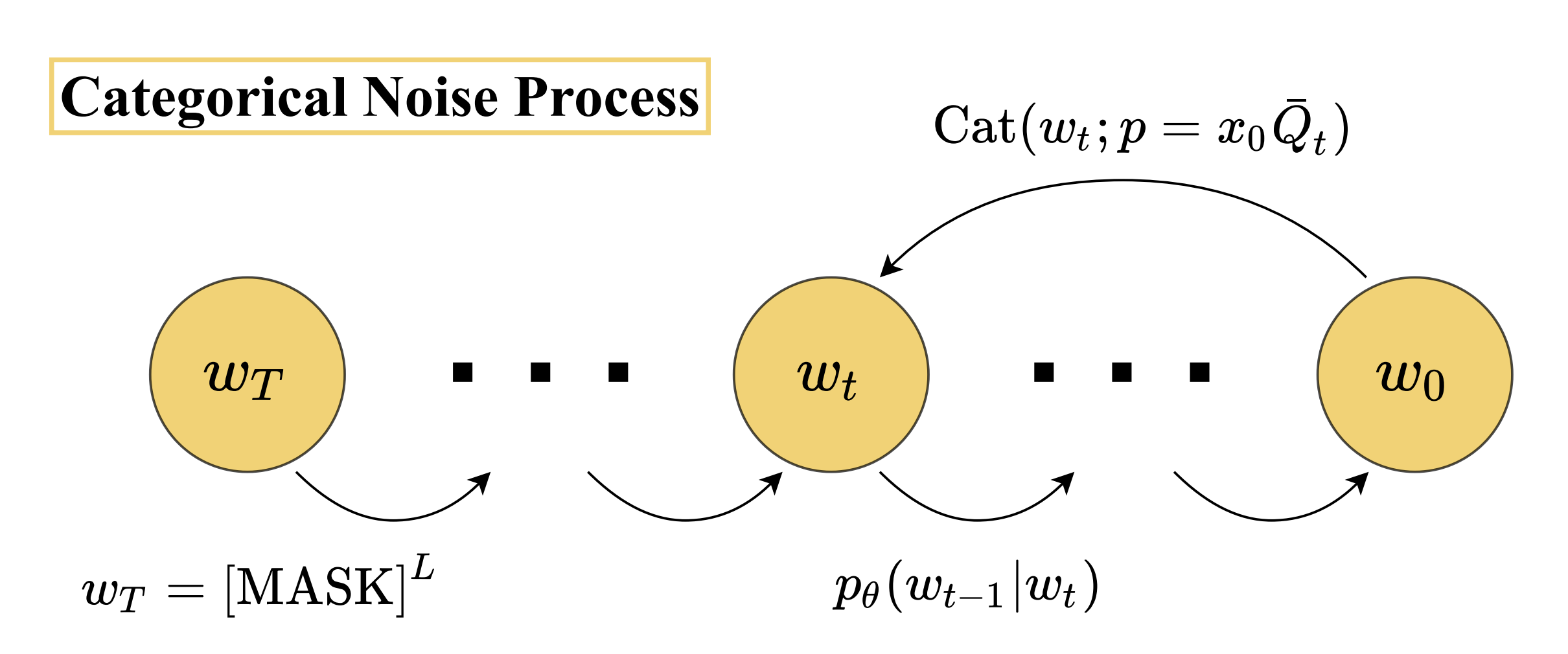
실험에서는 그래프 색칠, 스도쿠, N‑퀸 등 전통적인 CSP 베치마크를 사용했으며, 특히 변수 수가 수천에 달하고 제약 밀도가 0.3~0.7 사이인 대규모 인스턴스에서도 높은 성공률을 기록했다. 비교 대상으로는 SAT‑Solver 기반의 CDCL, 로컬 서치 기반의 WalkSAT, 그리고 최근의 신경망 기반 CSP 솔버인 N…