정확한 Zoeppritz 방정식을 활용한 비선형 진폭‑오프셋 역전
읽는 시간: 2 분
...
📝 원문 정보
- Title: Nonlinear seismic amplitude versus offset inversion using the exact Zoeppritz equation
- ArXiv ID: 2512.13172
- 발행일: 2025-12-15
- 저자: Wiktor Waldemar Weibull, Nisar Ahmed
📝 초록 (Abstract)
진폭‑변화‑오프셋(AVO) 역전 기술은 모델링된 지진 응답을 관측 데이터에 맞추어 탄성 물성을 추정하도록 설계된다. 역문제 해결을 위해서는 목표 목적 함수를 최소화해야 하며, 이를 위해 흔히 그래디언트 기반 최적화 방법이 사용된다. 그러나 이러한 방법의 효율성과 정확성은 목표 함수의 그래디언트를 계산하는 방식에 크게 좌우된다. 본 연구에서는 정확한 Zoeppritz 방정식을 다층 매질에 대해 이산화하고, 인접 상태(adjoint‑state) 방법을 이용해 명시적인 해석 그래디언트를 도출하였다. 도출된 식은 컨볼루션 기반 목적 함수에 대한 P파 속도, S파 속도 및 밀도에 대한 그래디언트를 제공한다. 인접 상태 기반 해법은 수치적 근사 없이 그래디언트를 고정밀도로 계산함으로써 계산 효율성을 크게 향상시킨다. 또한 정확한 Zoeppritz 방정식을 사용함으로써 지하층 간 탄성 물성 대비가 약한 경우에 발생하는 한계를 극복한다. 최소제곱 목표 함수를 비선형 제한 메모리 quasi‑Newton 알고리즘으로 최소화한다. 우리는 P·S 파 속도와 밀도 모델을 포함하는 지진 역전 문제에 대해 정확한 Zoeppritz 방정식의 해석 그래디언트 해법이 효과적임을 입증한다. 1차원 시추공 로그 기반 및 2차원 합성 지진 데이터를 다양한 잡음 수준에서 검증한 뒤, 노르웨이 북해 트롤 유전의 2차원 현장 데이터에 적용하였다. 결과는 제안된 역전 프레임워크가 탄성 물성 모델을 안정적이고 신뢰성 있게 추정함을 보여준다.💡 논문 핵심 해설 (Deep Analysis)
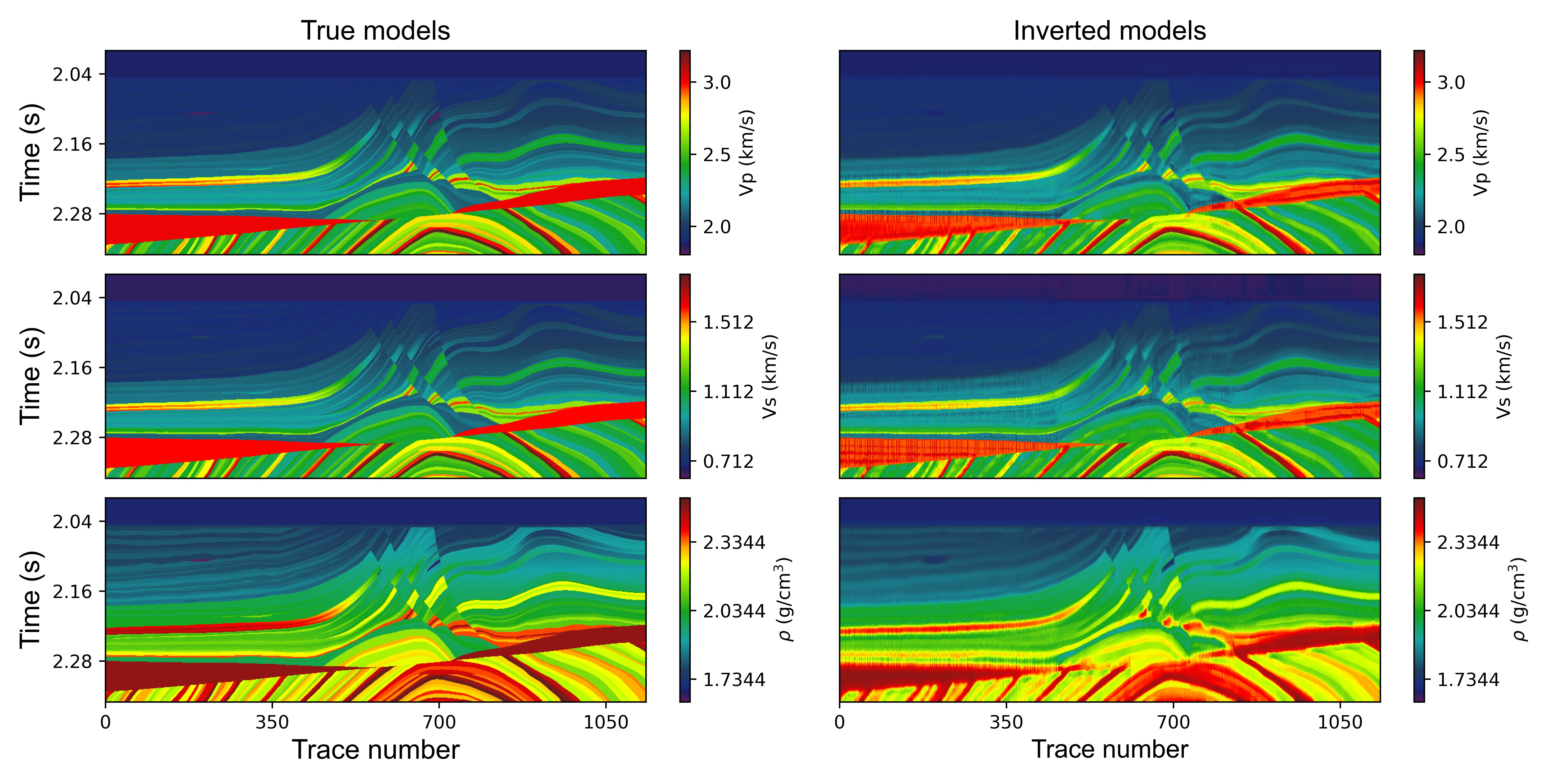
이 연구는 정확한 Zoeppritz 방정식을 다층 매질에 대해 이산화하고, 인접 상태(adjoint‑state) 방법을 적용해 목표 함수의 미분을…