동적 시스템에서 임계 전이 탐지를 위한 잡음 강인 대조 학습

2025년 12월 14일

읽는 시간: 3 분

...

#System #Detection #Learning

📝 원문 정보

Title: Noise-robust Contrastive Learning for Critical Transition Detection in Dynamical Systems
ArXiv ID: 2512.12523
발행일: 2025-12-14
저자: Wenqi Fang, Ye Li

📝 초록 (Abstract)

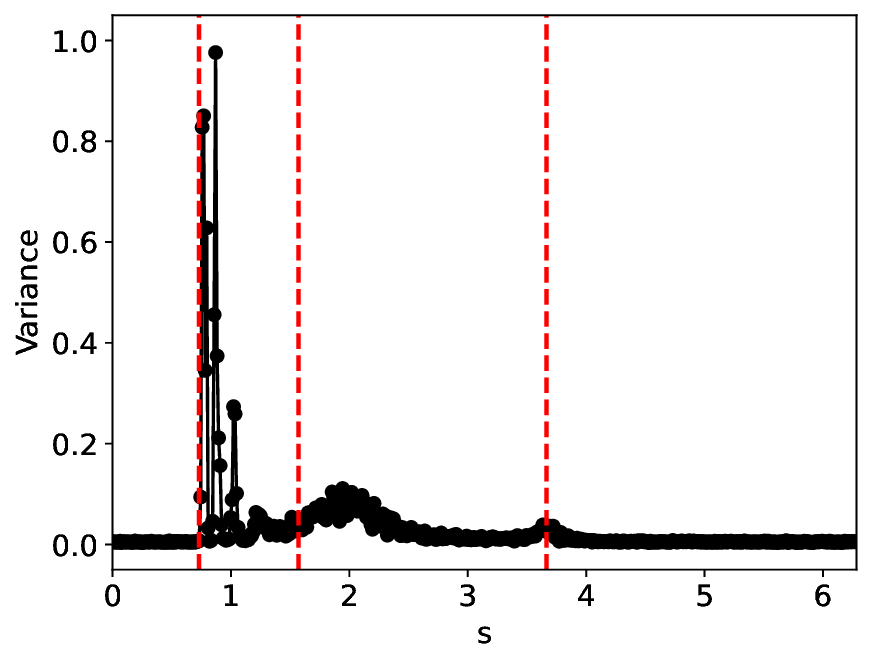
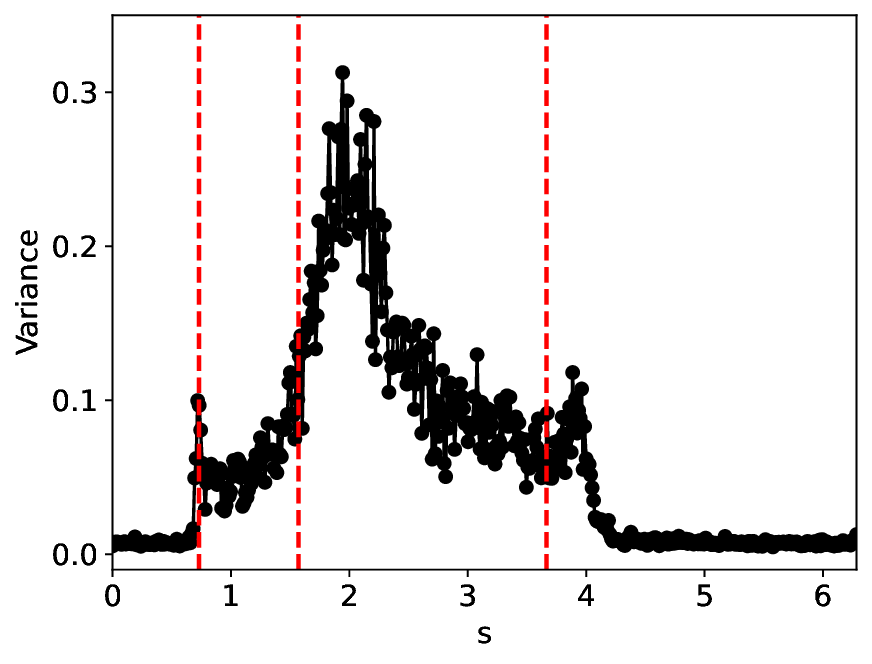
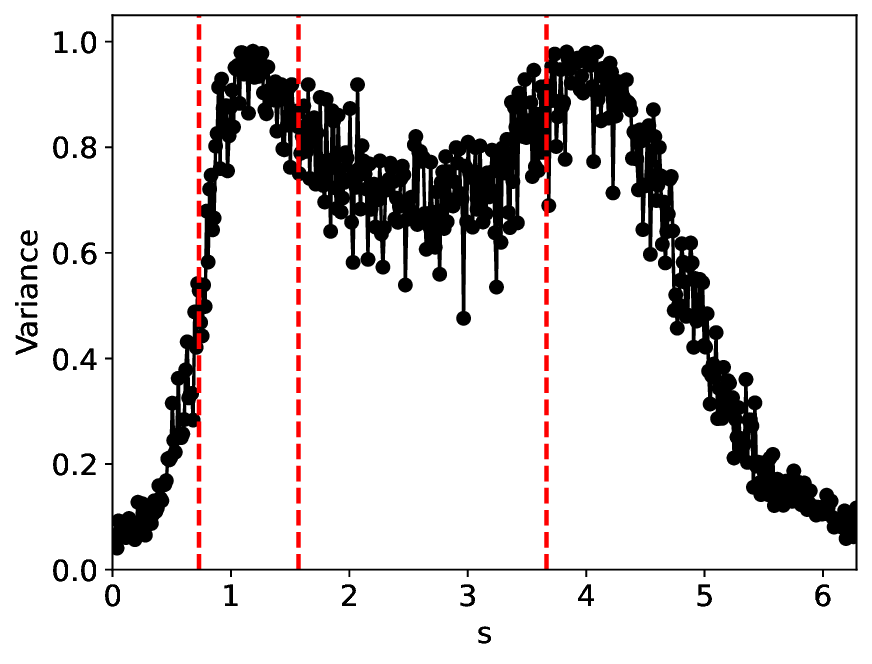
복잡하고 잡음이 많은 시계열 데이터에서 임계 전이를 탐지하는 것은 과학·공학 전반에 걸친 핵심 과제이다. 이러한 전이는 저차원 순서 매개변수의 출현으로 예고될 수 있으나, 고진폭의 확률적 변동에 가려지기 쉽다. 기존 딥 뉴럴 네트워크 기반 대조 학습은 전이 탐지에 유망하지만, 과다 파라미터화와 무관한 잡음에 대한 민감성으로 정확도가 떨어진다. 본 연구는 특이값 분해(SVD) 기반 신경망 구조와 반직교성 제약 학습 알고리즘을 도입해 전통적 대조 학습의 성능을 유지하면서 경량화와 잡음 저항성을 크게 향상시킨다. 광범위한 실험 결과, 제안 방법이 기존 기법과 동등한 전이 식별 능력을 보이며, 특히 잡음이 심한 상황에서 현저히 우수한 견고성을 나타냄을 확인하였다.

💡 논문 핵심 해설 (Deep Analysis)

이 논문은 동적 시스템의 임계 전이(critical transition)를 사전에 감지하기 위한 새로운 대조 학습(contrastive learning) 프레임워크를 제시한다. 기존 연구에서는 복잡계의 전이를 포착하기 위해 고차원 시계열을 저차원 임베딩으로 압축하고, 정상 상태와 전이 전후를 구분하는 손실 함수를 최적화하는 방식이 주를 이루었다. 그러나 이러한 접근은 네트워크 규모가 커질수록 과적합 위험이 커지고, 특히 높은 신호‑대‑잡음비(SNR) 환경에서 잡음이 학습에 혼입되어 전이 신호를 왜곡한다는 한계가 있었다.

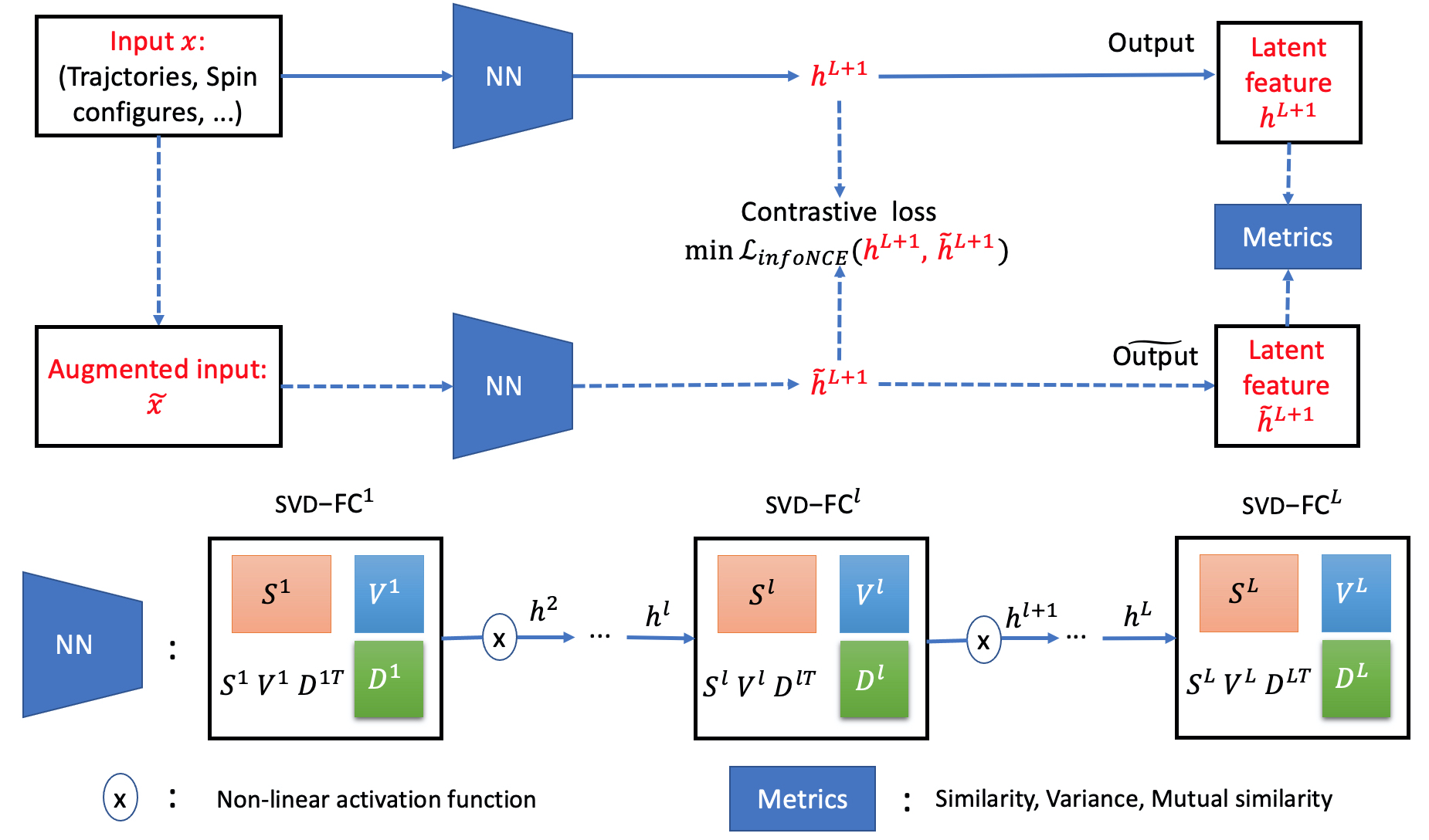
논문이 제안한 핵심 아이디어는 두 가지다. 첫째, 신경망 가중치를 직접 SVD 형태로 초기화하고, 주요 특이값만을 보존함으로써 파라미터 수를 근본적으로 감소시킨다. 이는 ‘핵심 모드’만을 학습하도록 강제하여 불필요한 자유도를 제거한다. 둘째, 학습 과정에서 가중치 행렬이 반직교성(semi‑orthogonality) 조건을 만족하도록 제약을 가한다. 반직교성은 행렬이 서로 거의 직교함을 의미하므로, 입력 변동이 출력에 비선형적으로 증폭되는 것을 억제하고, 잡음 성분이 서로 상쇄되도록 만든다. 이러한 제약은 기존의 L2 정규화보다 강력하게 잡음에 대한 로버스트성을 부여한다.

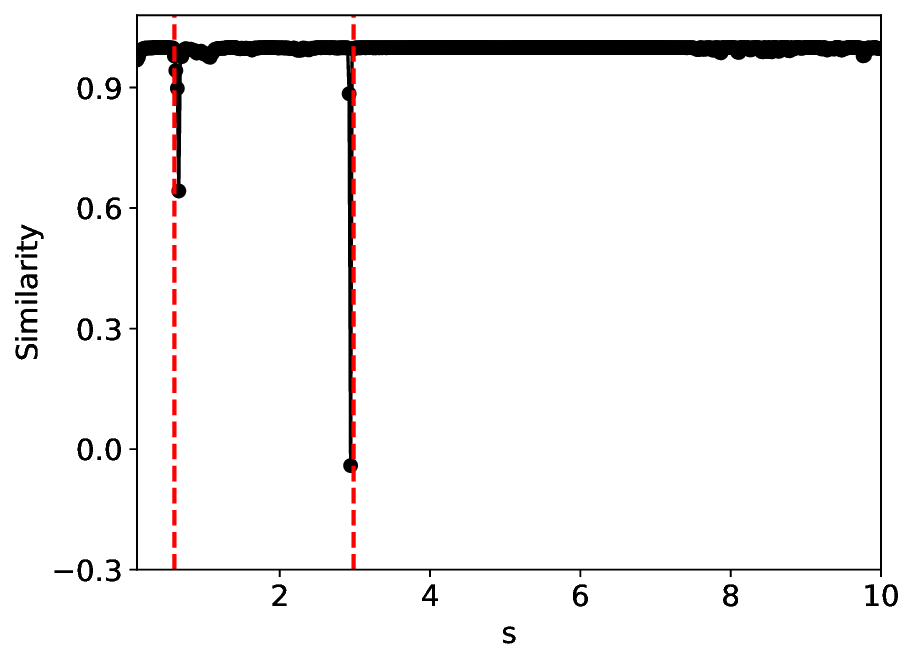
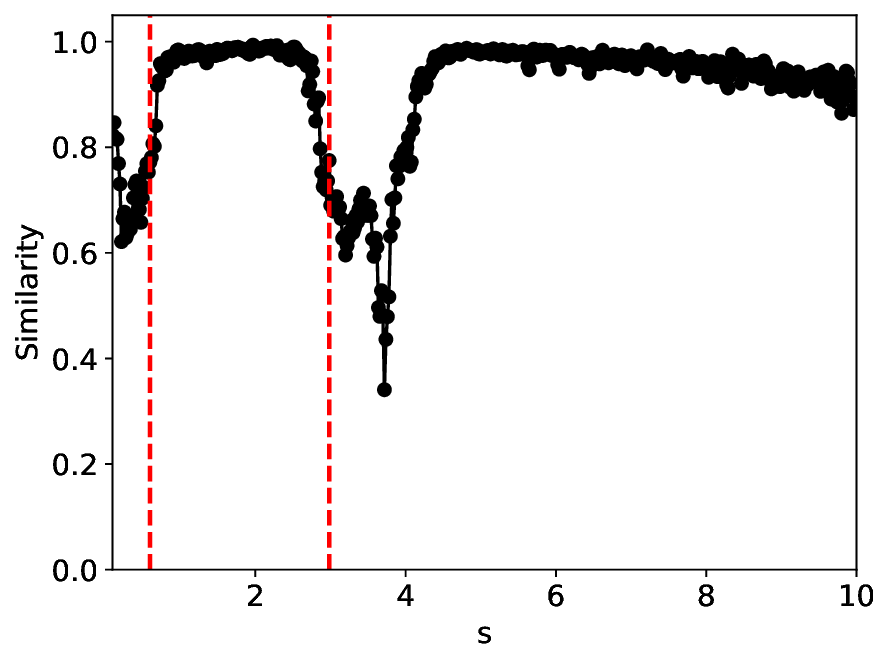
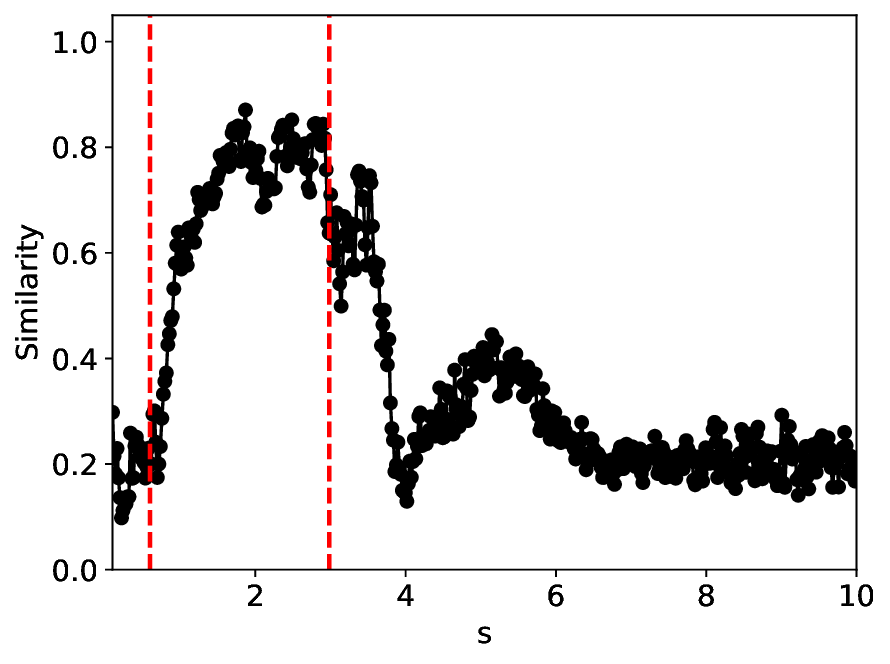
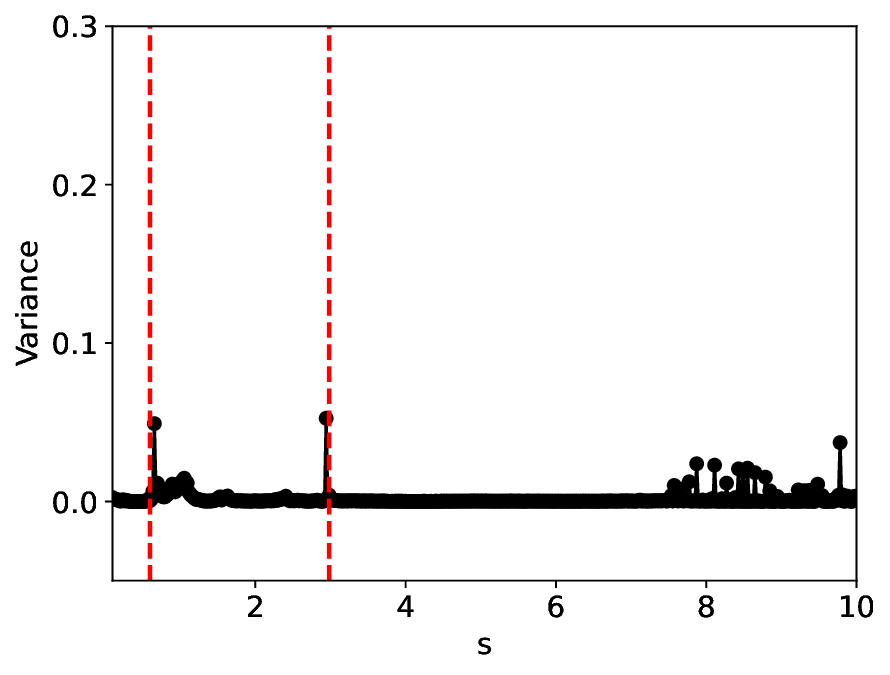
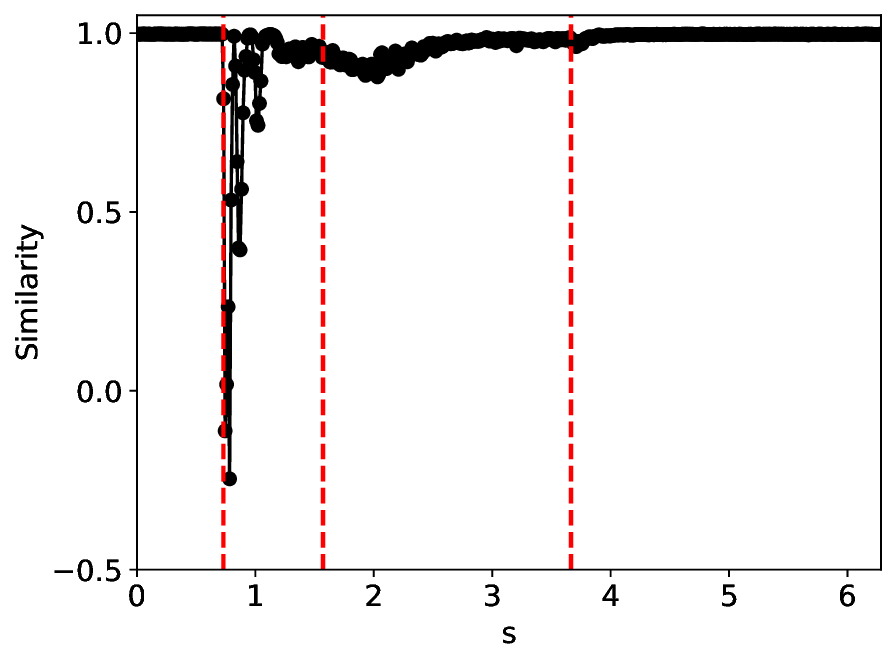
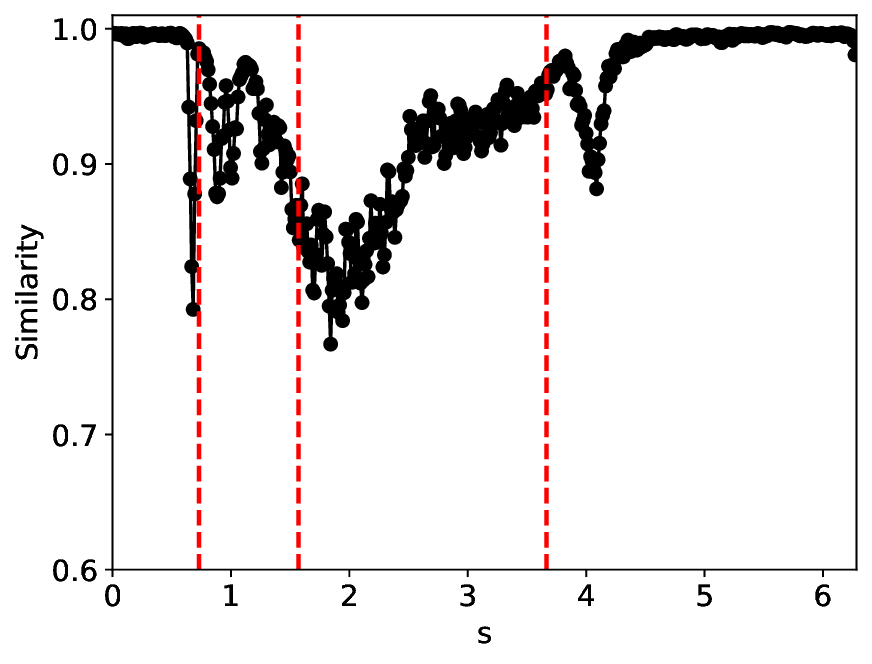
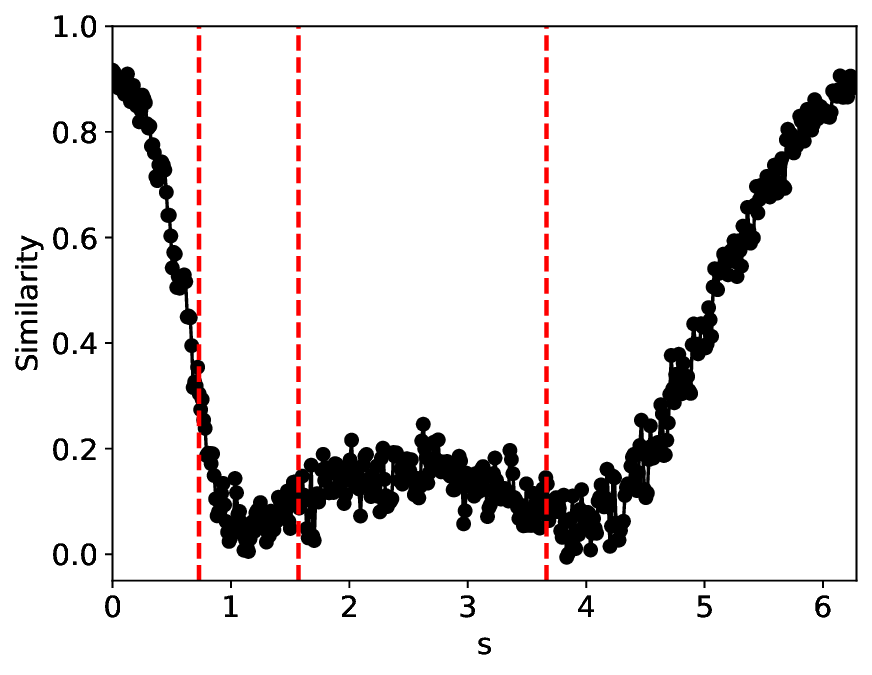
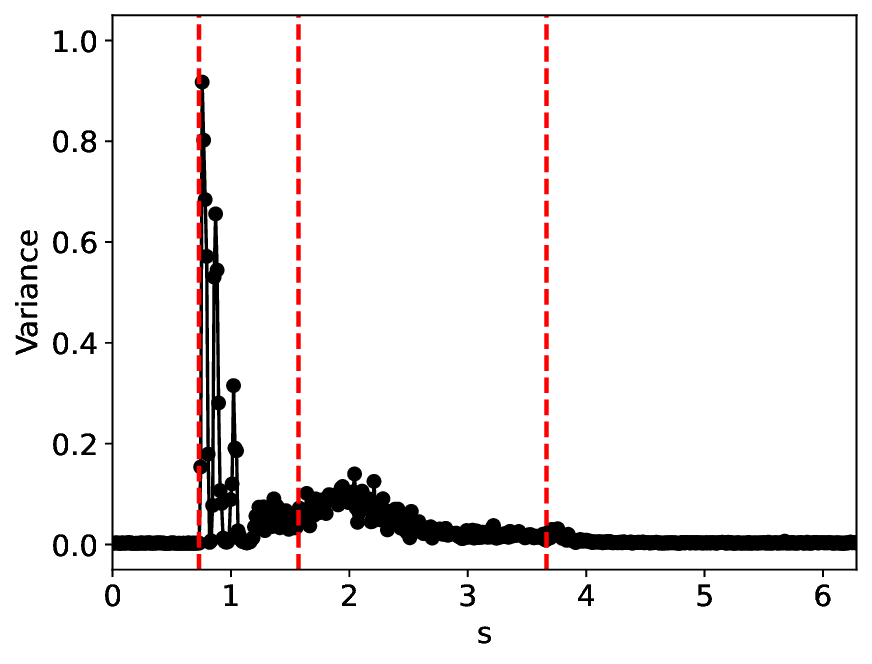
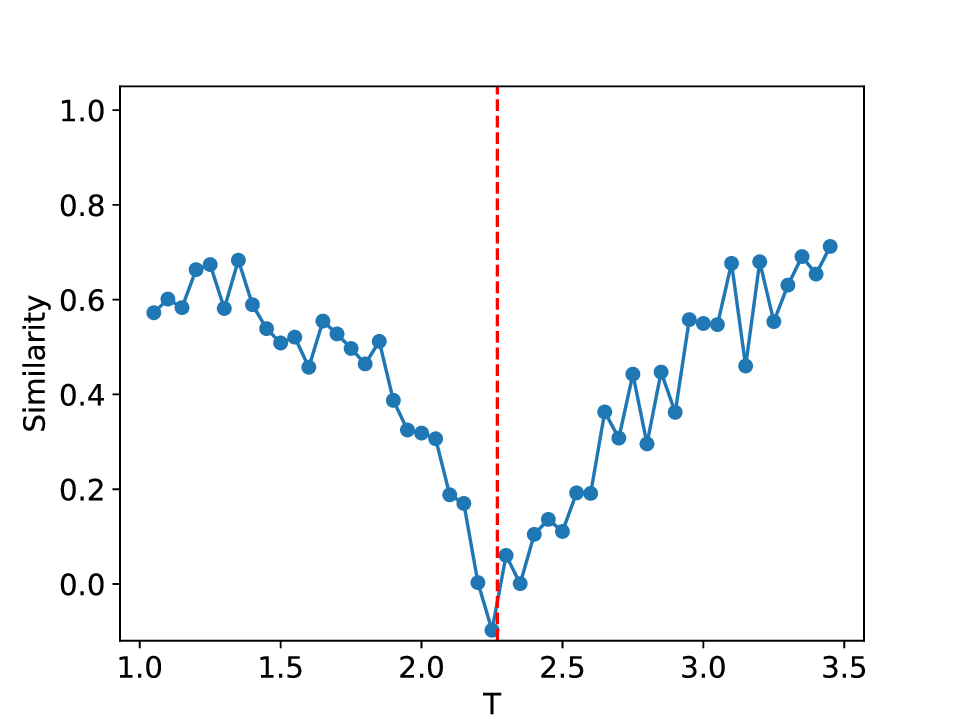
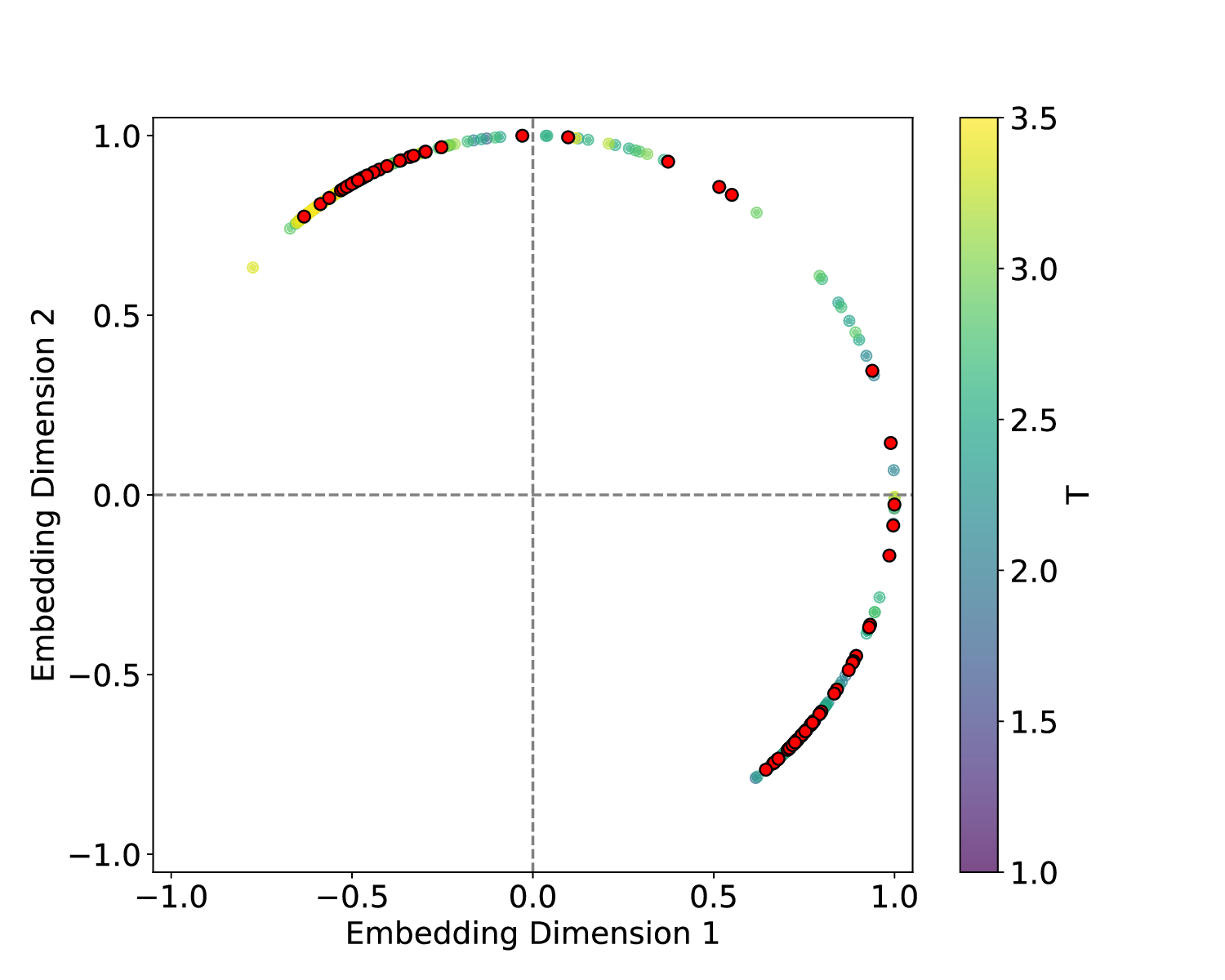
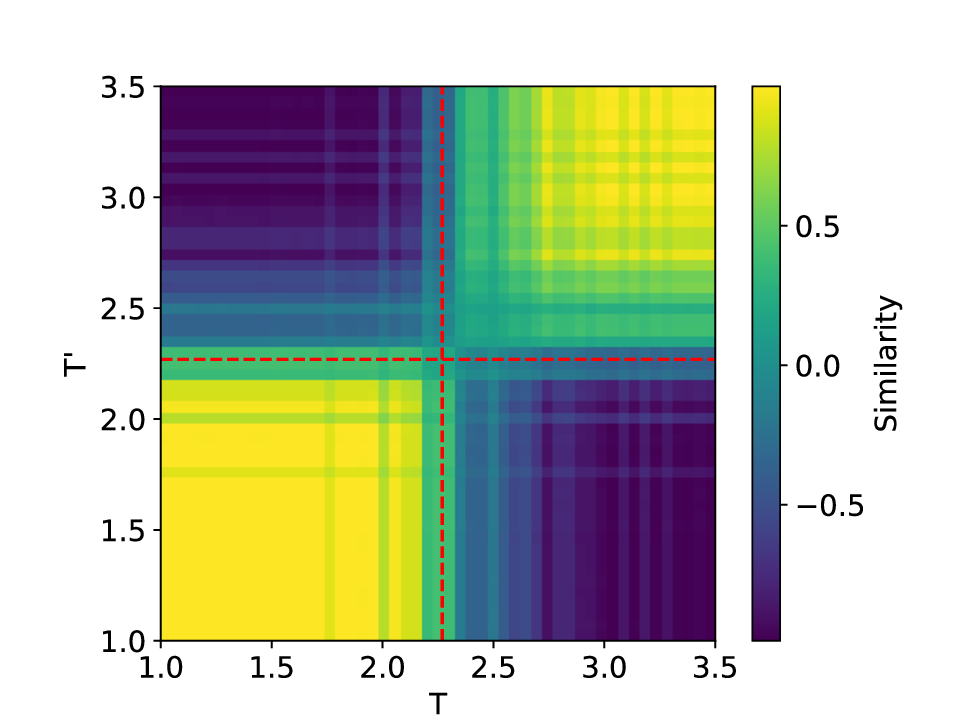
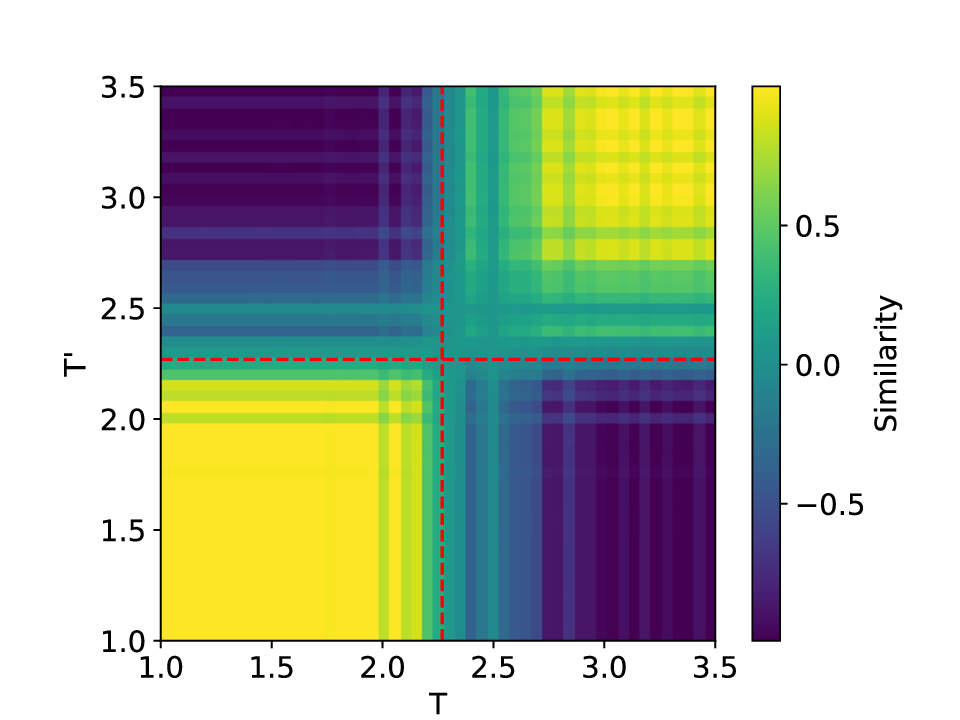
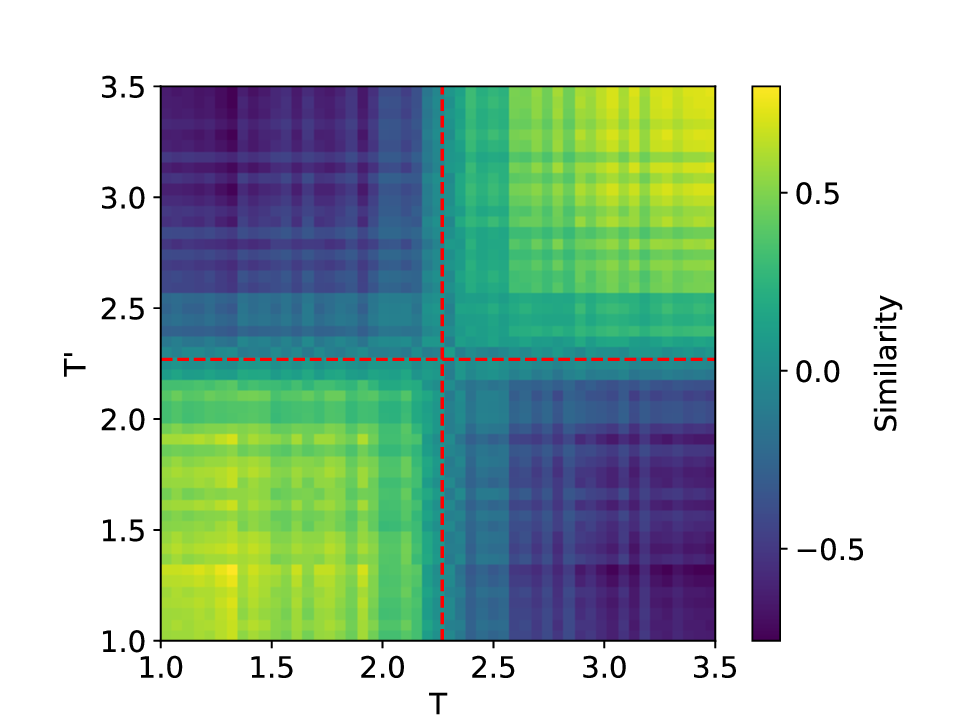
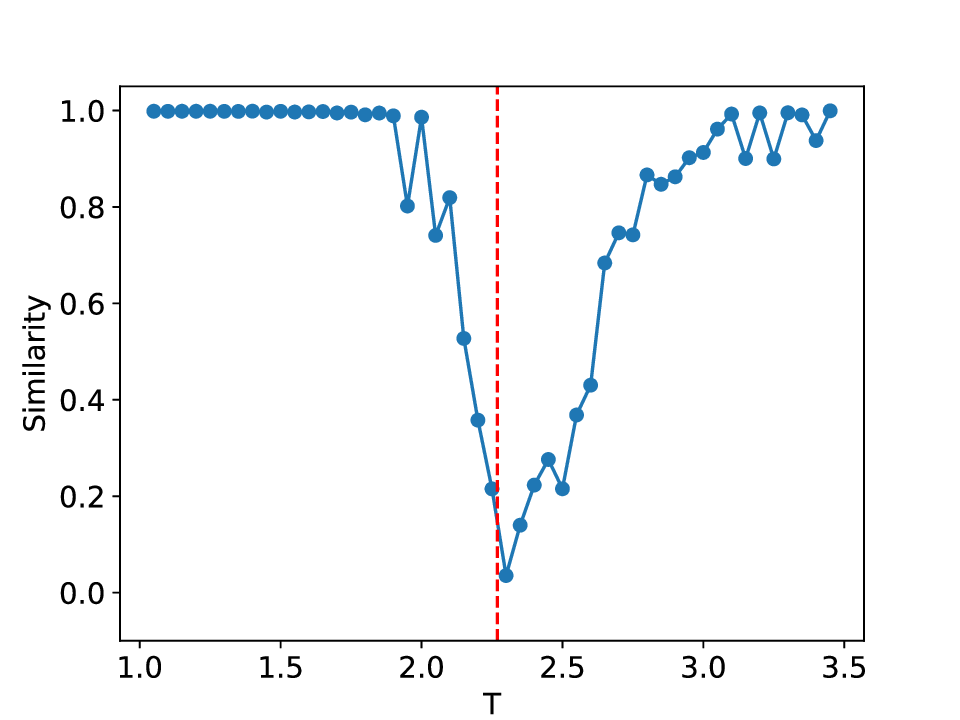
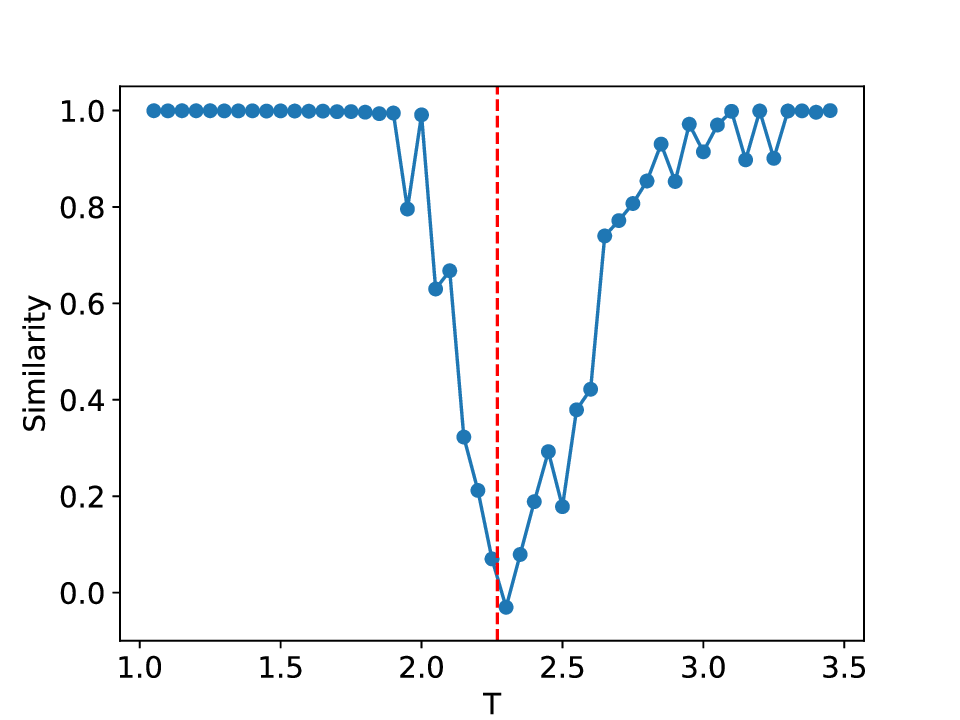
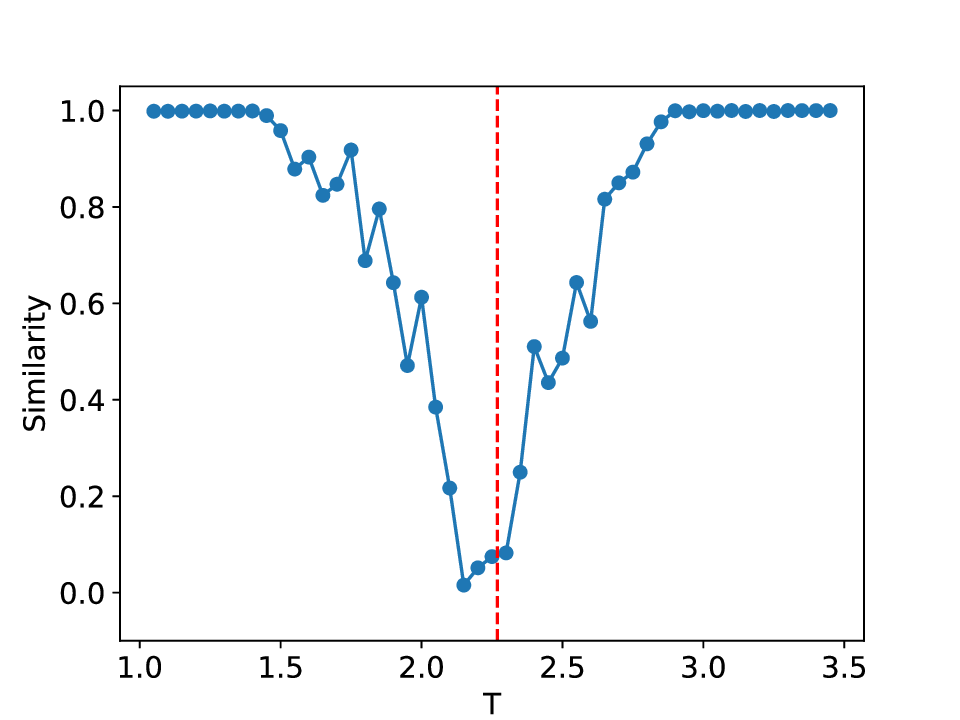
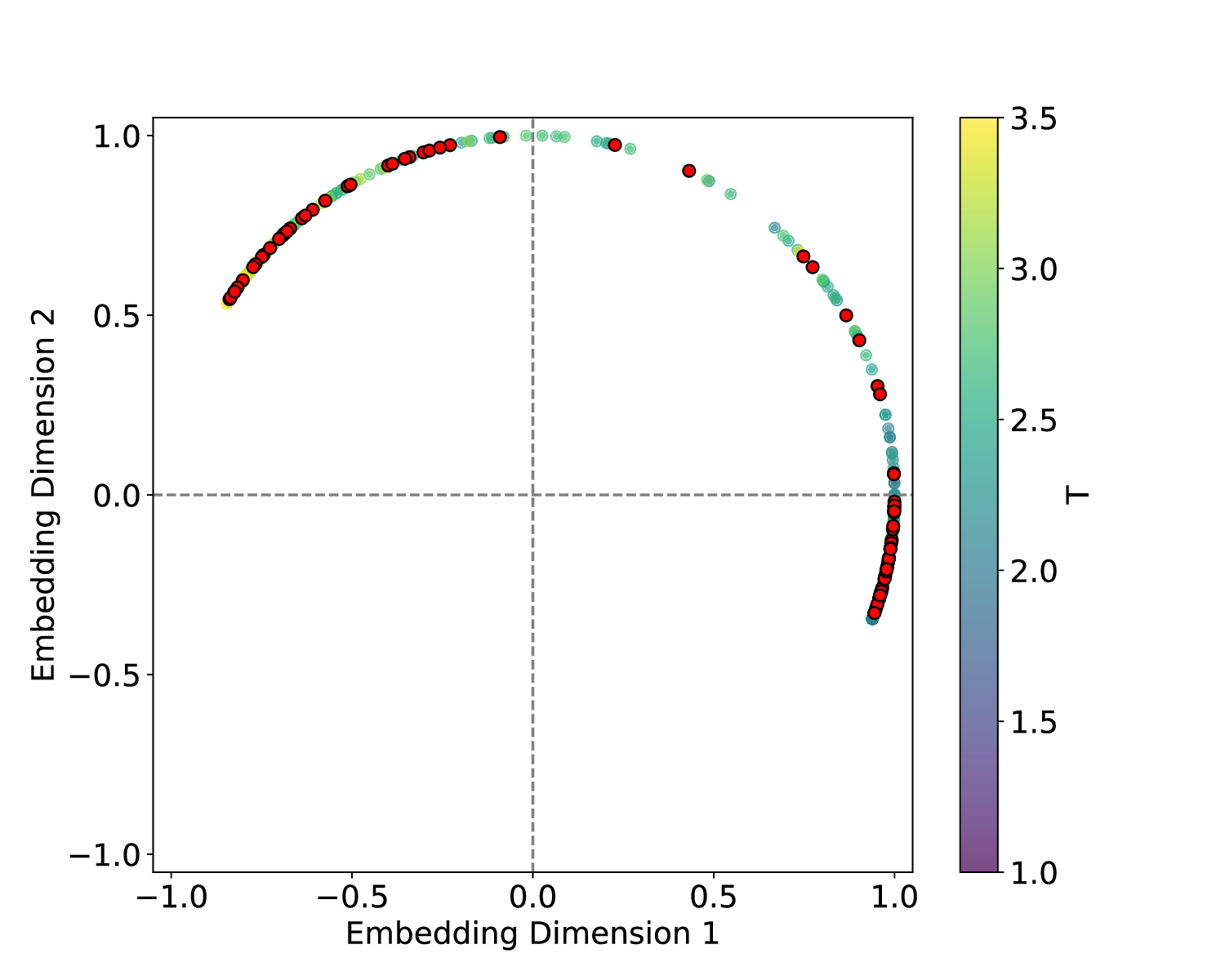
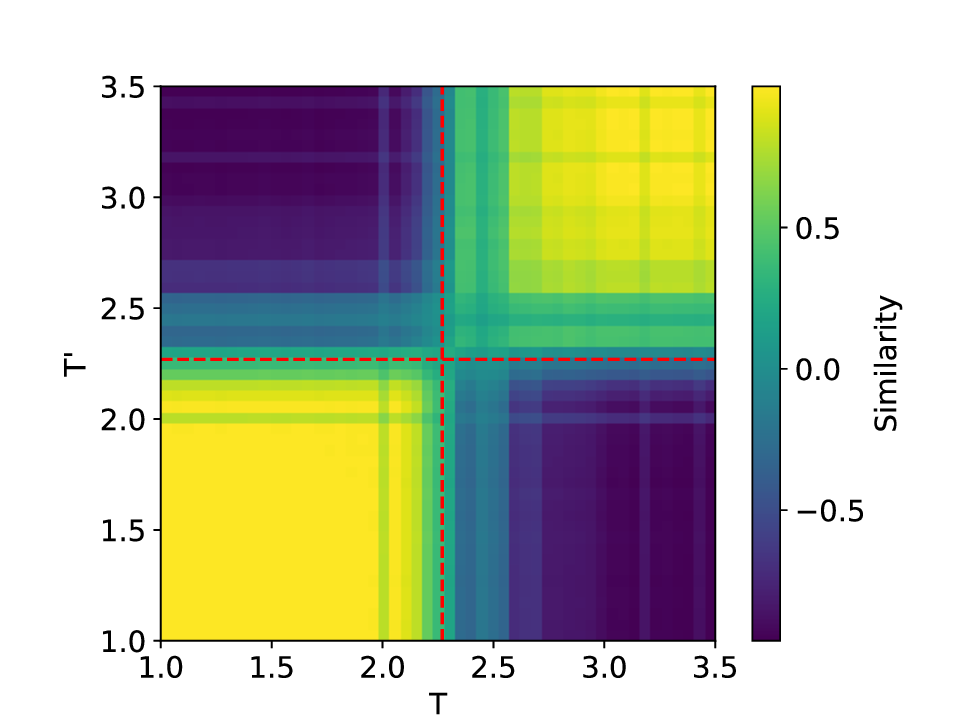
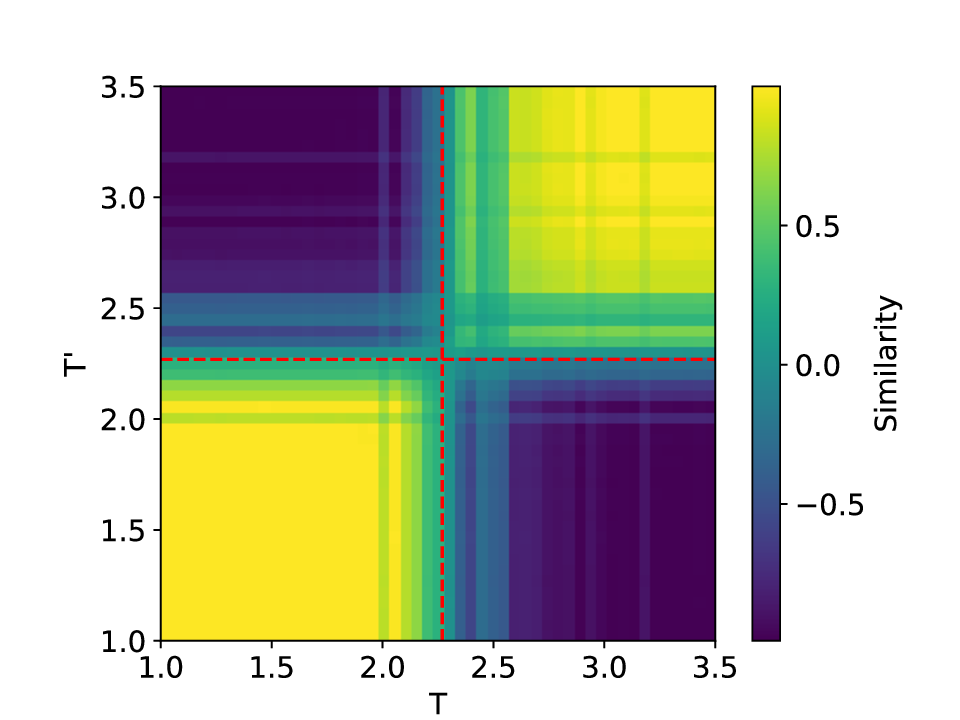
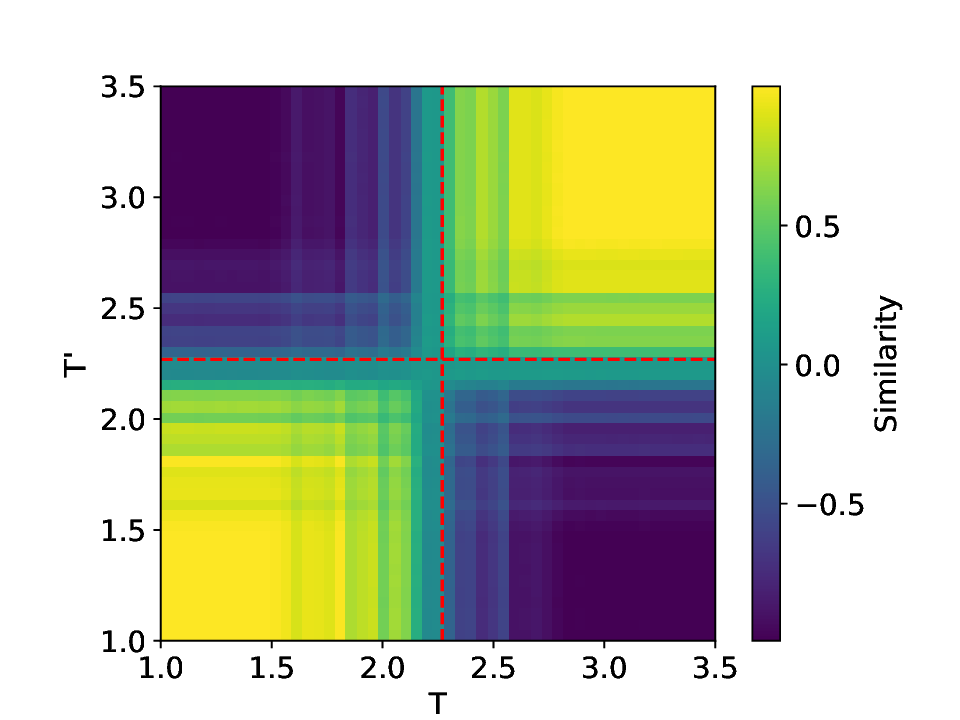
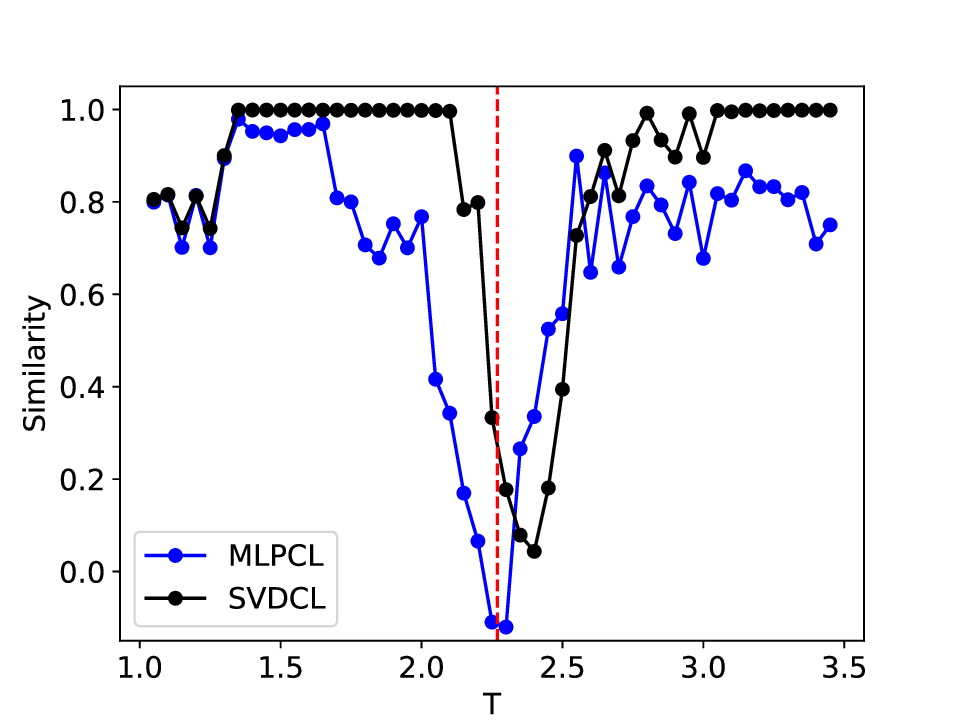
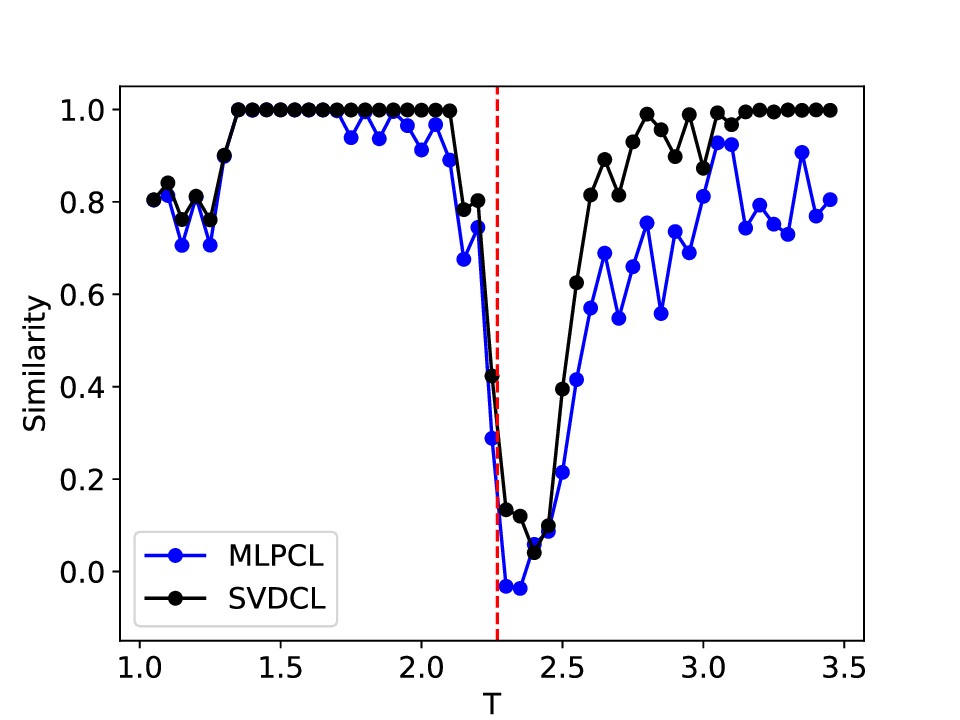
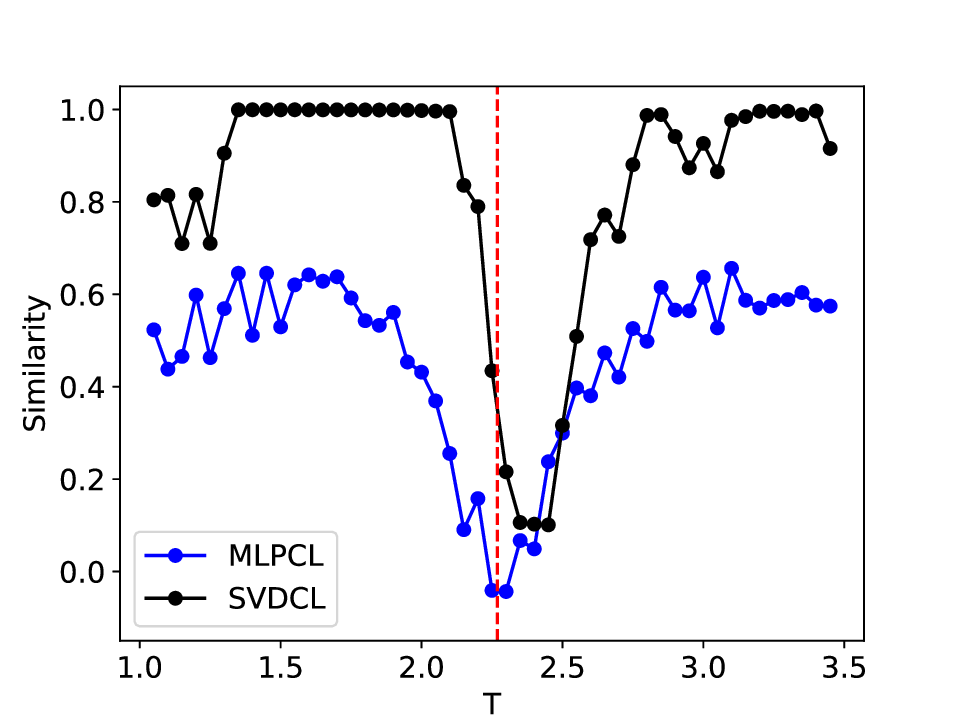
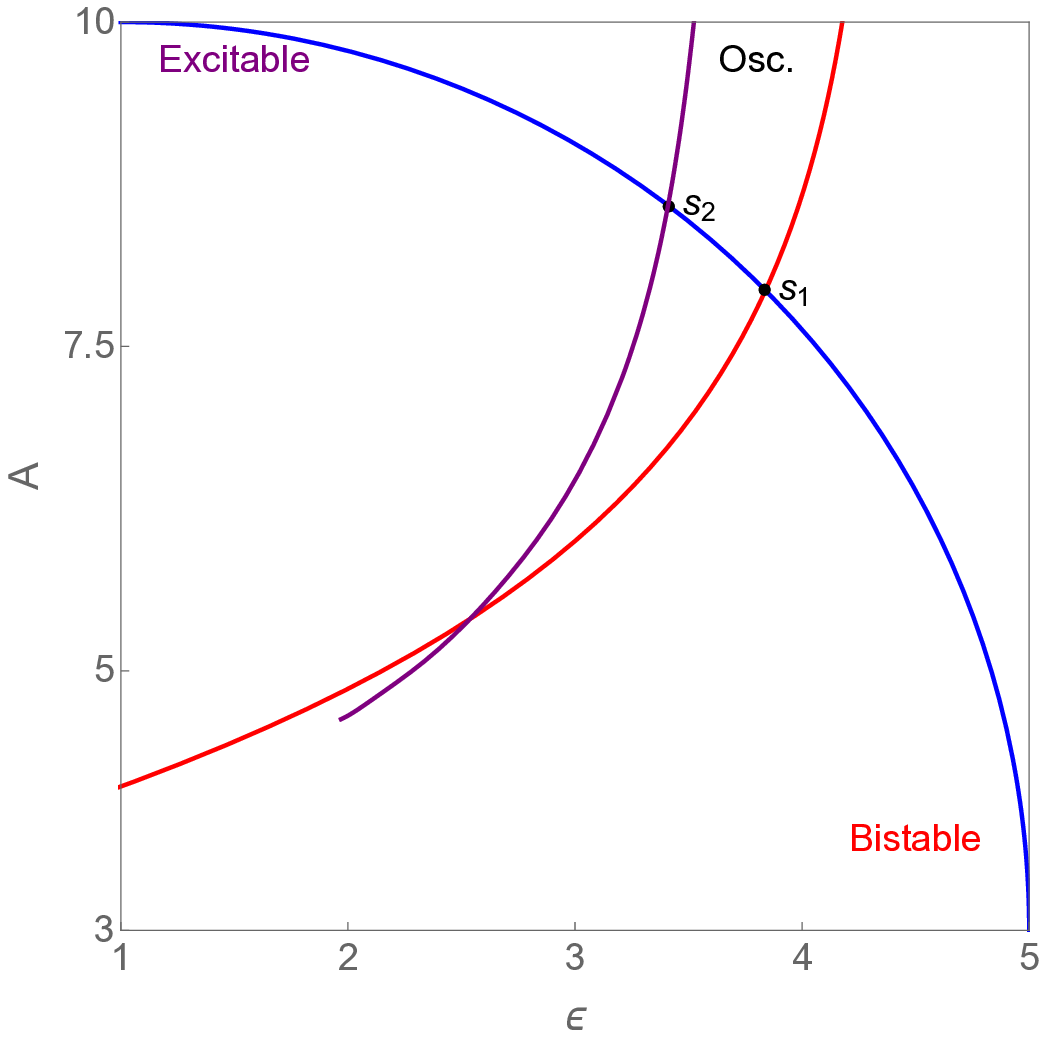
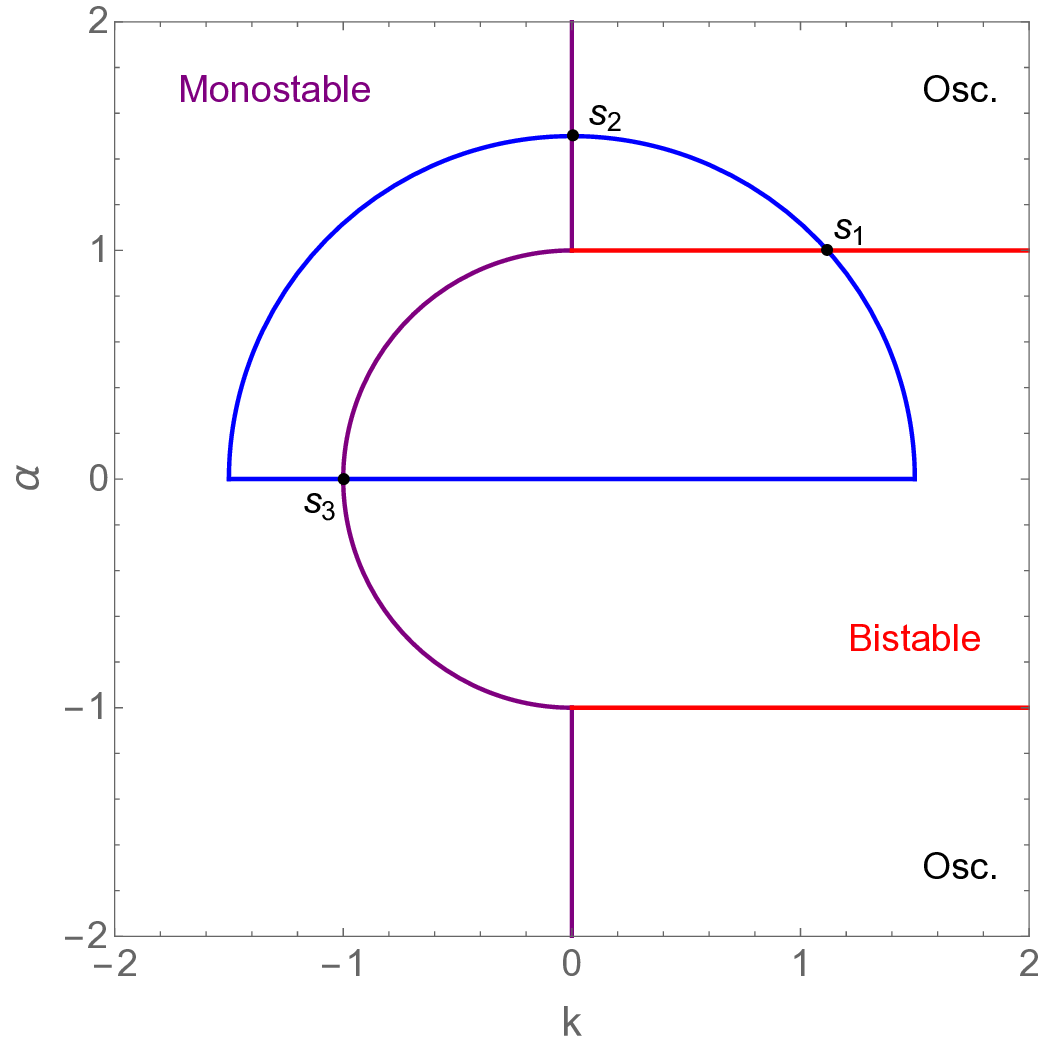
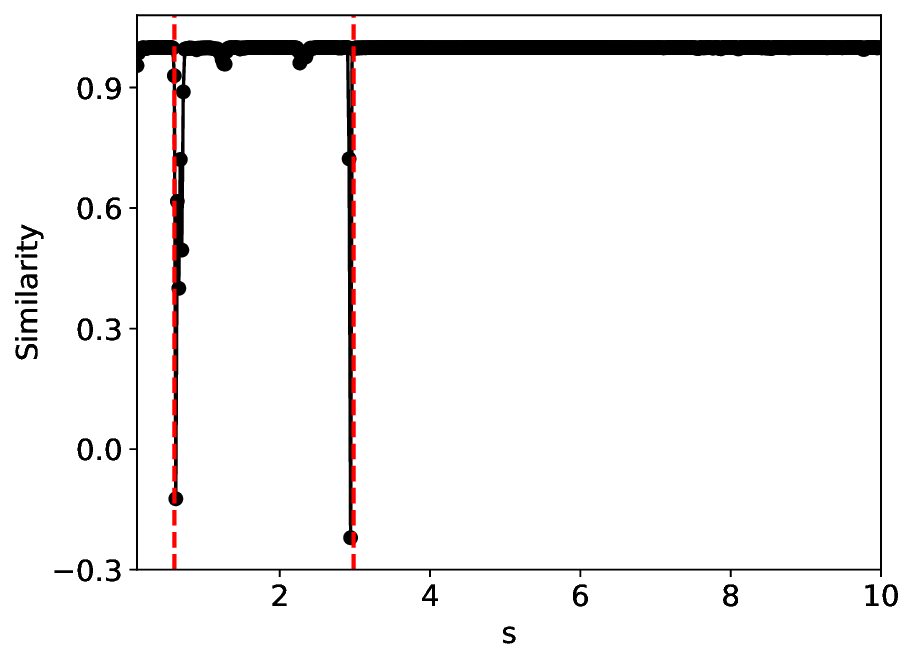
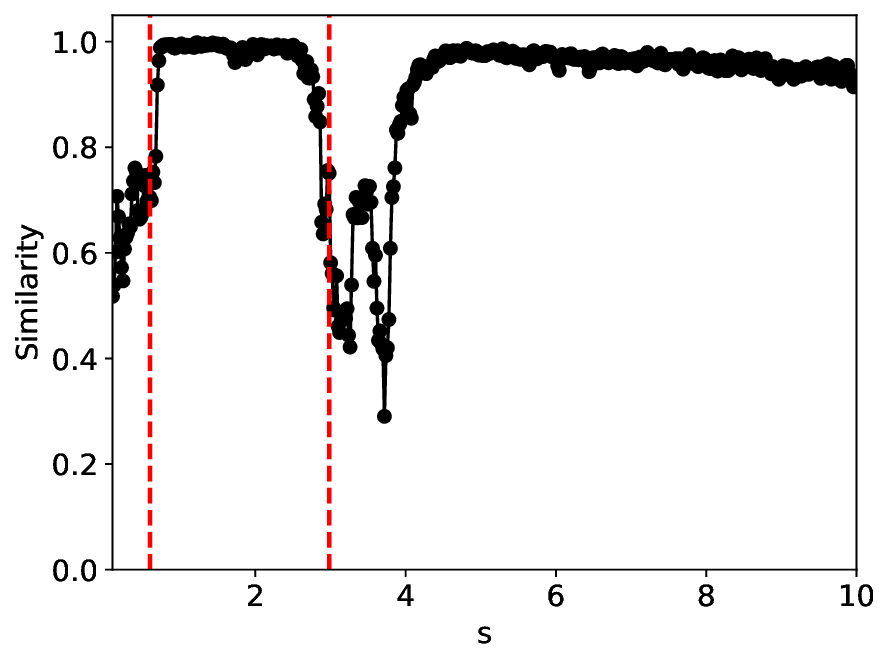
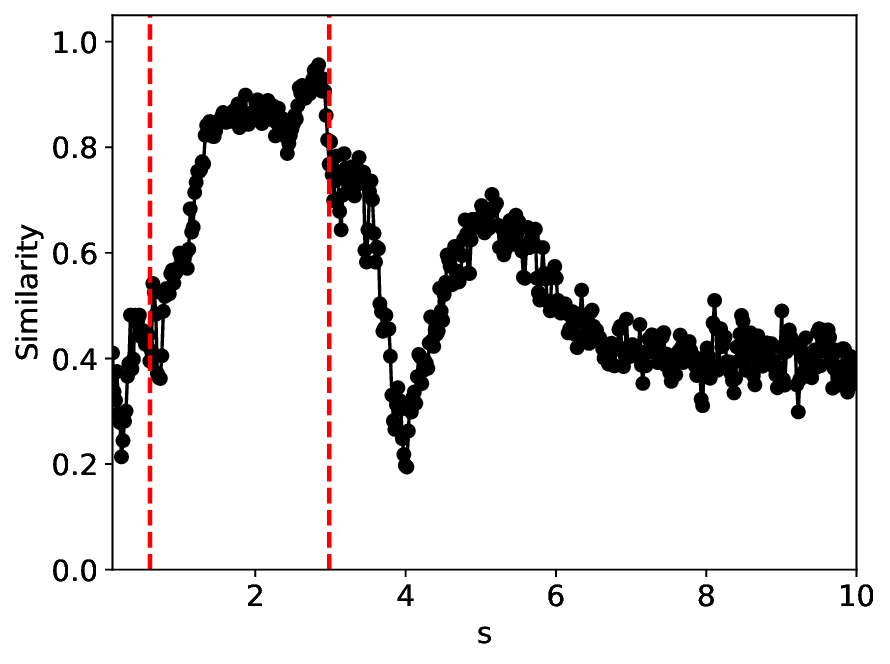
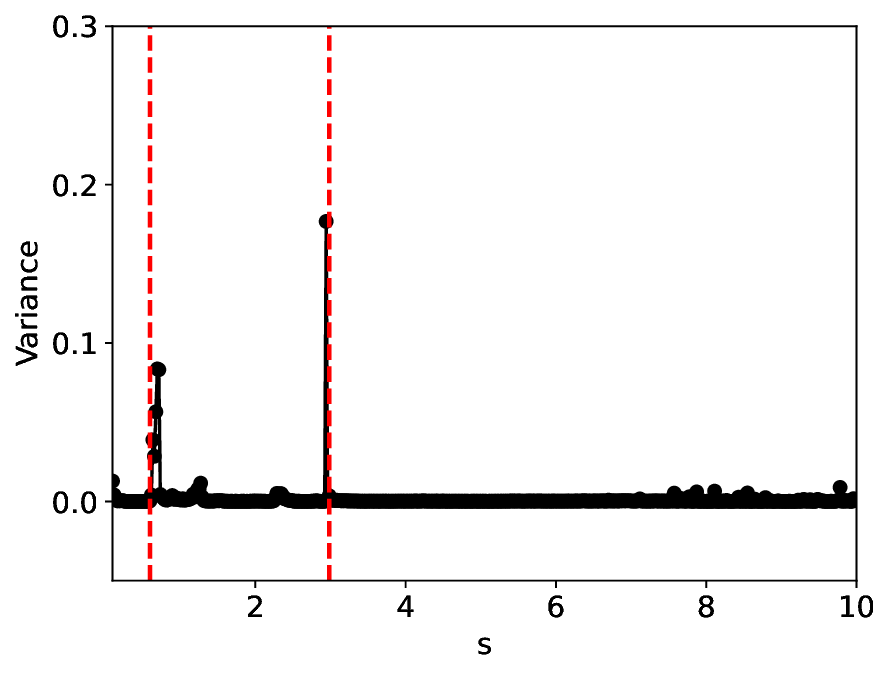
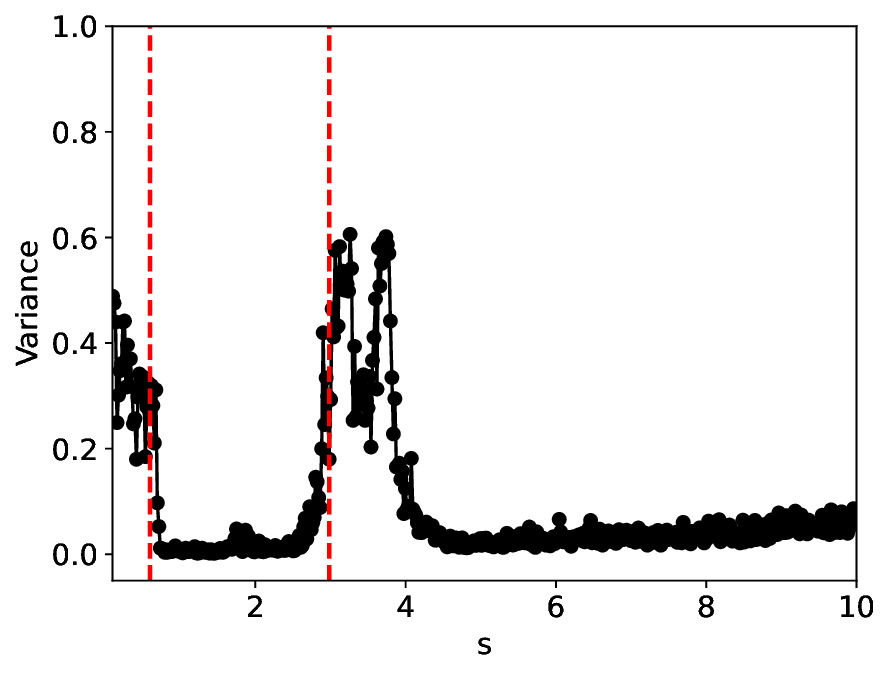
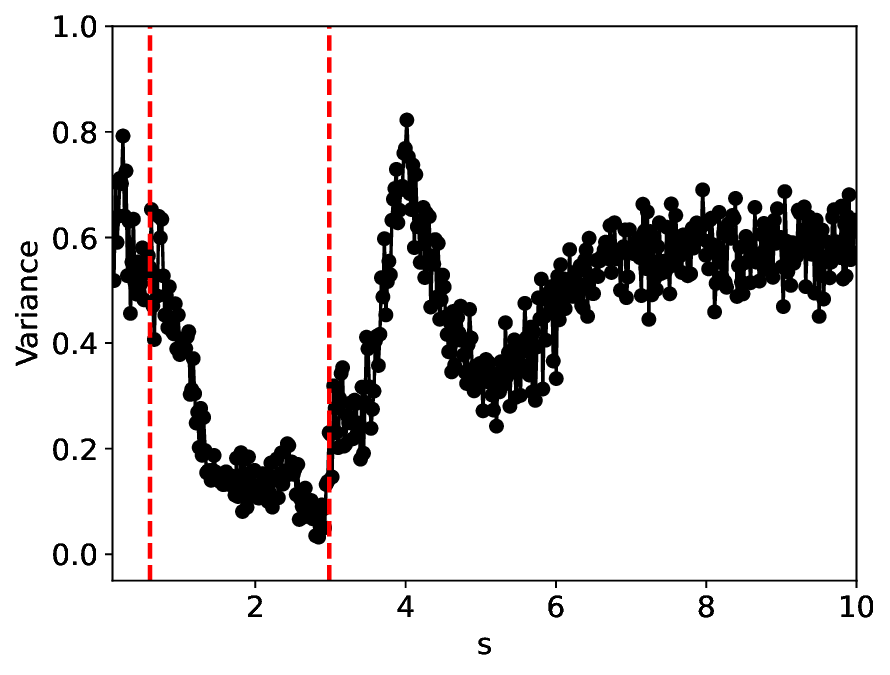
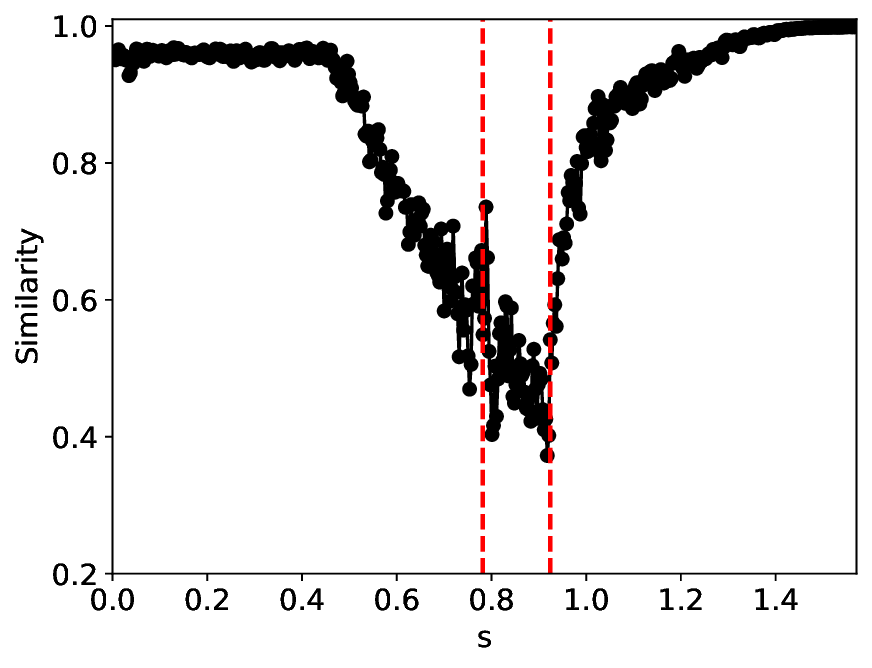
실험에서는 표준 대조 학습 모델과 비교해 동일한 데이터셋(예: 로렌즈 시스템, 생태학적 모델)에서 정확도와 F1‑score가 거의 동일했지만, 신호‑대‑잡음비를 0 dB 수준까지 낮춘 경우 제안 모델의 성능 저하가 현저히 적었다. 또한 파라미터 수가 70 % 이상 감소했음에도 불구하고 추론 속도가 1.5배 가량 빨라졌으며, 메모리 사용량도 크게 절감되었다.

이러한 결과는 두 가지 의미 있는 함의를 가진다. 첫째, 복잡계 연구에서 대규모 딥러닝 모델에 의존하지 않고도 충분히 강인한 전이 탐지가 가능함을 보여준다. 둘째, 반직교성 제약이라는 수학적 원리를 활용한 경량화 전략이 다른 시계열 분석 분야(예: 금융 변동성 예측, 뇌파 이상 탐지)에도 일반화될 가능성을 시사한다. 다만, 현재는 SVD 기반 초기화와 반직교성 유지가 계산적으로 추가 비용을 요구하므로, 실시간 스트리밍 데이터에 적용하기 위해서는 효율적인 근사 알고리즘이 필요하다. 향후 연구에서는 이러한 제약을 동적하게 조정하거나, 비선형 커널 SVD와 결합해 더욱 복잡한 비선형 전이를 포착하는 방향을 모색할 수 있다.