생성 경로 붕괴와 확산 스티어링을 위한 기준 및 교정 방법
읽는 시간: 2 분
...
📝 원문 정보
- Title: On the Collapse of Generative Paths: A Criterion and Correction for Diffusion Steering
- ArXiv ID: 2512.10339
- 발행일: 2025-12-11
- 저자: Ziseok Lee, Minyeong Hwang, Sanghyun Jo, Wooyeol Lee, Jihyung Ko, Young Bin Park, Jae-Mun Choi, Eunho Yang, Kyungsu Kim
📝 초록 (Abstract)
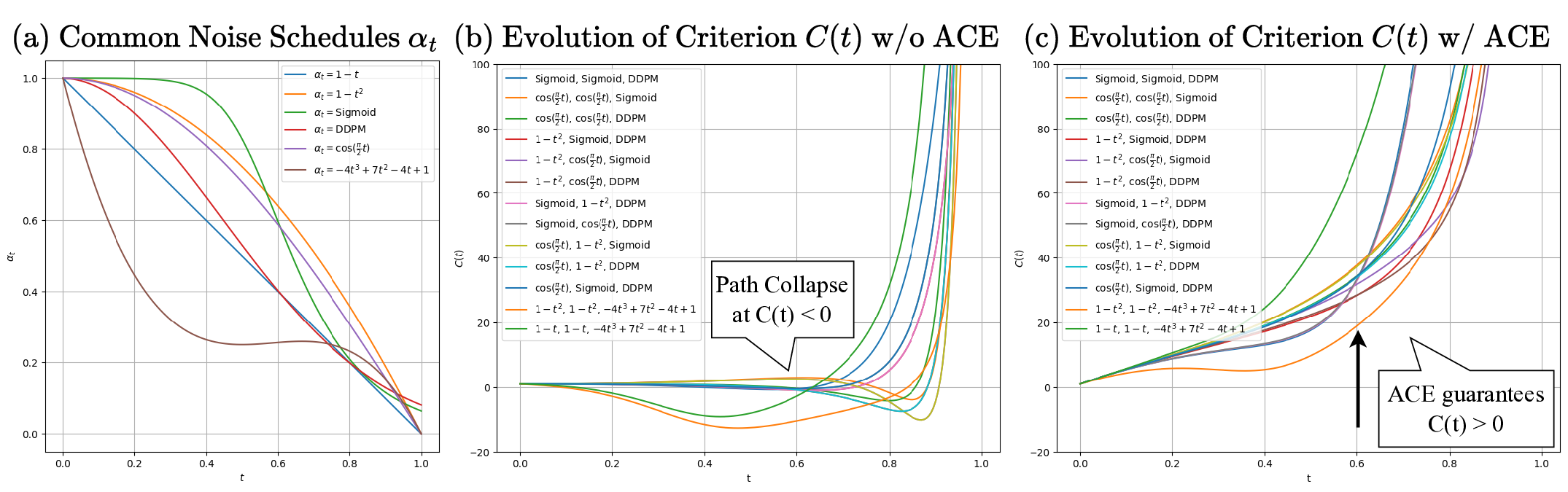
추론 단계에서 스티어링을 이용하면 사전 학습된 확산·플로우 모델을 재학습 없이 새로운 작업에 적용할 수 있다. 널리 쓰이는 비율‑밀도 방식은 여러 모델의 확률 밀도 궤적을 양수 혹은 음수 지수로 재가중하여 시간에 따라 정의된 목표 경로를 만든다. 그러나 이 구성에는 아직 정형화되지 않은 치명적인 실패 모드인 ‘마진 경로 붕괴’가 존재한다. 이는 중간 단계의 밀도가 정규화될 수 없게 되지만 시작·끝점은 여전히 유효한 현상이다. 서로 다른 노이즈 스케줄이나 데이터셋으로 학습된 이질적인 모델을 결합할 때 체계적으로 발생한다. 특히 분자 설계에서 de‑novo, 컨포머, 포켓 조건부 모델을 결합해 유연한 포즈 스캐폴드 장식을 수행할 때 흔히 나타난다. 본 논문은 두 가지 주요 기여를 제시한다. 첫째, 노이즈 스케줄과 지수만으로 붕괴 여부를 정확히 예측하는 간단한 경로 존재 기준을 도출한다. 둘째, 시간 가변 지수를 허용하는 Feynman‑Kac 스티어링을 확장한 Adaptive path Correction with Exponents (ACE)를 도입해 항상 유효한 확률 경로를 보장한다. 2차원 합성 벤치마크와 유연 포즈 스캐폴드 장식 실험에서 ACE는 붕괴를 완전히 제거하고, 높은 가이던스 조합 생성이 가능하도록 하며, 분포 및 도킹 지표에서 상수 지수 기반 베이스라인 및 전용 스캐폴드 장식 모델을 능가한다. 우리의 연구는 이질적인 전문가들을 활용한 비율‑밀도 스티어링을 불안정한 휴리스틱에서 신뢰할 수 있는 제어 생성 도구로 전환한다.💡 논문 핵심 해설 (Deep Analysis)