텐서 압축 및 완전 양자화 기반 신경 PDE 솔버 학습

📝 원문 정보

• Title: Tensor-Compressed and Fully-Quantized Training of Neural PDE Solvers
• ArXiv ID: 2512.09202
• 발행일: 2025-12-10
• 저자: Jinming Lu, Jiayi Tian, Yequan Zhao, Hai Li, Zheng Zhang

📝 초록 (Abstract)

물리 기반 신경망(PINN)은 물리 법칙을 손실 함수에 내재시켜 편미분 방정식(PDE)을 푸는 새로운 접근법으로 주목받고 있다. 그러나 고차 자동미분, 대규모 텐서 연산, 그리고 전밀도 부동소수점 연산에 의존하는 구조 때문에 연산량과 메모리 요구가 크게 늘어나, 자원 제한이 있는 플랫폼에서는 활용이 어려웠다. 이를 극복하고자 본 연구는 엣지 디바이스에서도 확장 가능하고 에너지 효율적인 PINN 학습 프레임워크를 제안한다. 프레임워크는 (1) 역전파 시 데이터 복제를 없애는 정사각형 블록 MX(SMX) 형식을 이용한 혼합 정밀도 학습, (2) 언더플로우를 완화하는 차분 기반 양자화 스키마를 적용한 Stein 추정기(SE) 손실 계산, (3) 양자화 오차 누적을 줄이는 텐서‑트레인(TT) 레이어의 부분 재구성 스키마(PRS)를 통합한다. 또한 제안된 프레임워크의 성능을 최대한 활용하도록 설계된 정밀도 확장형 하드웨어 가속기 PINTA를 구현하였다. 2‑D 포아송, 20‑D 해밀턴‑자코비‑벨만(HJB), 100‑D 열 방정식 실험에서 제안 방법은 전밀도·비압축 기준과 동등하거나 더 높은 정확도를 유지하면서 5.5배~83.5배의 속도 향상과 159.6배~2324.1배의 에너지 절감을 달성하였다. 이 연구는 엣지 디바이스에서 실시간 PDE 해결을 가능하게 하며, 대규모 과학 컴퓨팅의 에너지 효율성을 크게 향상시킬 전망이다.

💡 논문 핵심 해설 (Deep Analysis)

Physics‑Informed Neural Networks(PINN)은 전통적인 수치 해법과 달리 신경망 자체에 미분 방정식의 물리적 제약을 손실 함수로 삽입함으로써, 복잡한 경계·초기 조건을 자연스럽게 만족시키는 장점을 갖는다. 그러나 실제 적용 단계에서 두드러지는 병목은 크게 세 가지로 요약할 수 있다. 첫째, PINN은 고차 자동미분을 반복 수행해야 하므로 연산 그래프가 급격히 복잡해지고, 이 과정에서 중간 텐서가 다중 복제되어 메모리 사용량이 폭증한다. 둘째, 신경망 가중치와 활성값을 전밀도(32‑bit) 부동소수점으로 유지하면 연산량과 전력 소모가 크게 늘어나, 배터리 기반의 엣지 디바이스에서는 실시간 학습이 거의 불가능에 가깝다. 셋째, 고차원 PDE(예: 20‑D HJB, 100‑D Heat)에서는 파라미터 수 자체가 급격히 증가해 모델 압축이 필수적이다.

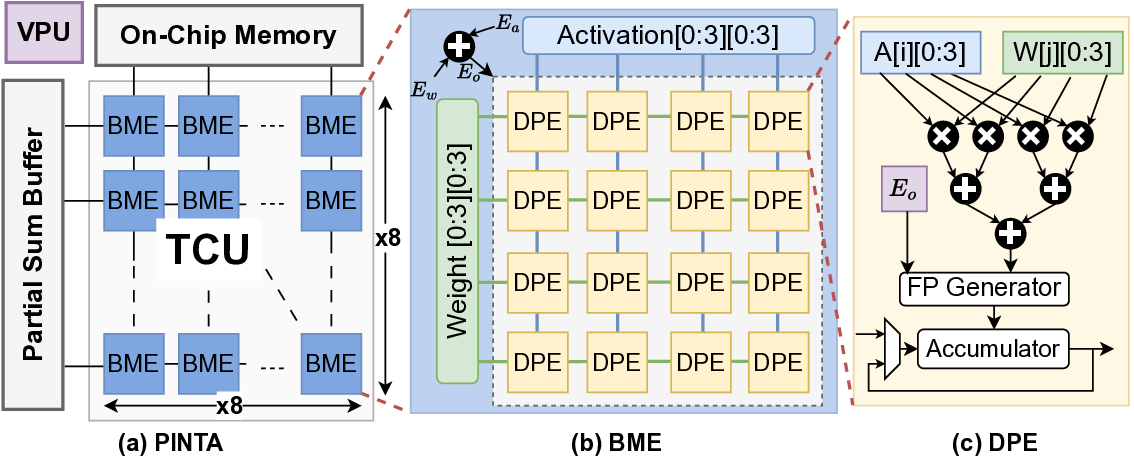
본 논문은 이러한 문제점을 동시에 해결하기 위해 세 가지 핵심 기술을 제안…

📄 논문 본문 발췌 (Translation)

...(본문 내용이 길어 생략되었습니다. 사이트에서 전문을 확인해 주세요.)