마법 보석: 마방진을 위한 다면체 프레임워크

📝 원문 정보

• Title: Magic Gems: A Polyhedral Framework for Magic Squares
• ArXiv ID: 2512.09170
• 발행일: 2025-12-09
• 저자: Kyle Elliott Mathewson

📝 초록 (Abstract)

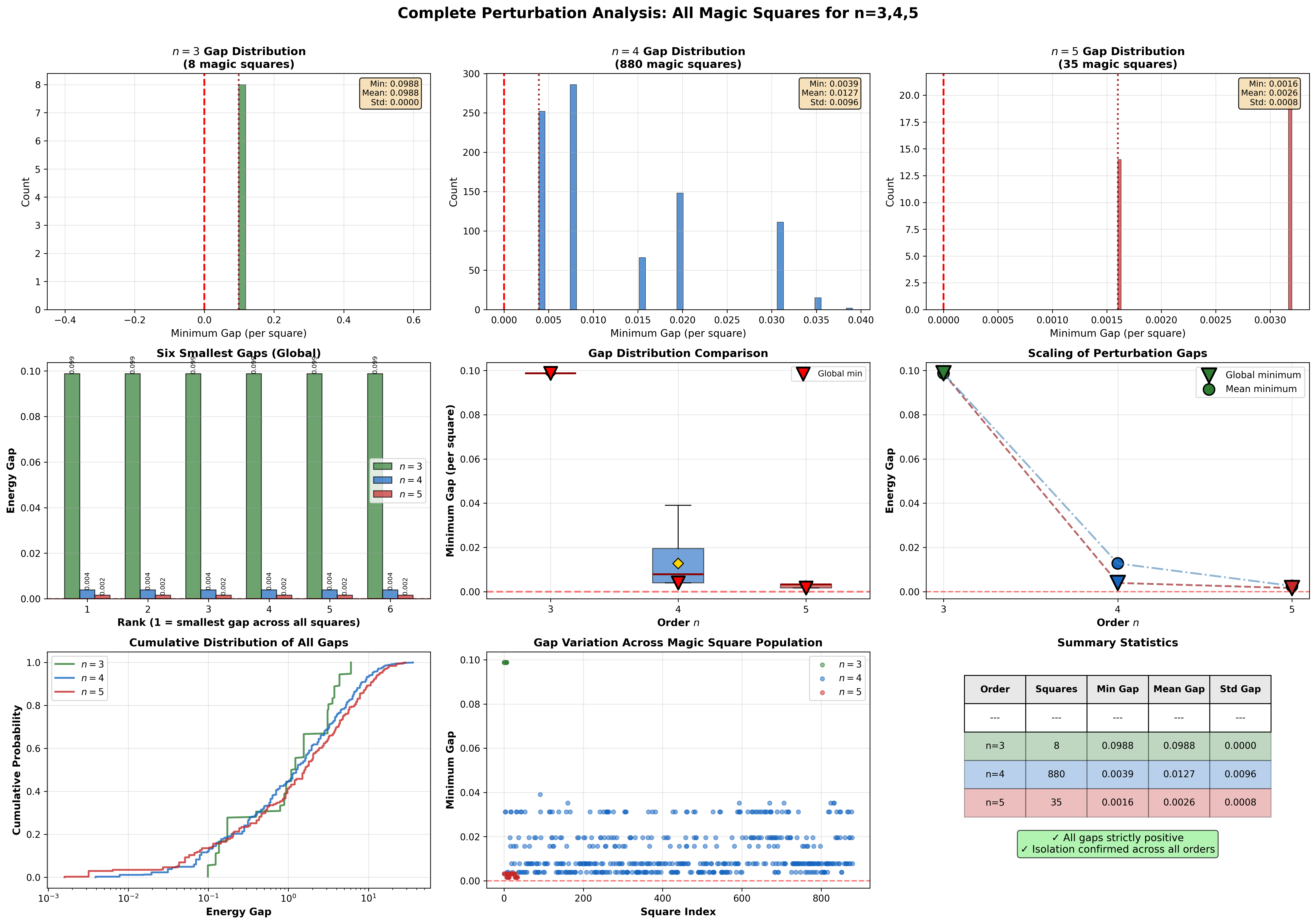
우리는 마방진을 3차원 다면체로 시각화하는 ‘마법 보석(Magic Gems)’을 제안한다. n × n 마방진을 중심 좌표 격자에 매핑하고, 각 셀 값을 수직 변위로 해석해 점 구름을 만든 뒤 그 볼록 껍질을 마법 보석으로 정의한다. 기존 연구가 마방진을 관성 모멘트와 같은 물리량에 연결한 것에 기반해, 본 구조는 마방진이 위치와 값 사이의 공분산이 모두 0임을 명시적으로 보여준다. 우리는 행·열·대각선 지시 변수와의 공분산 제곱합을 에너지 함수(공분산 에너지)로 정의하고, n ≥ 3에 대해 이 에너지가 완전히 0일 때와 마방진이 동치임을 증명한다. 이는 전통적인 ‘선합’ 정의를 통계적 직교 조건으로 변환한다. 네 개의 집합적 위치 지시 변수만을 이용한 저차 모드 완화는 n = 3에서는 완전 특성을 유지하지만, n ≥ 4에서는 더 넓은 클래스가 형성됨을 반례를 통해 확인한다. 섭동 분석을 통해 마방진이 에너지 풍경에서 고립된 지역 최소점임을 보이며, D₄(정사각형의 이변량) 대칭에 대해 불변성을 갖는다.

💡 논문 핵심 해설 (Deep Analysis)

본 논문은 마방진을 기존의 2차원 수열이 아니라 3차원 기하학적 객체로 재해석함으로써, 수학적 구조와 물리적 직관 사이의 다리를 놓는다. 먼저 n × n 격자를 원점에 중심을 두고, 각 셀 (i, j)의 값을 z‑축 방향의 높이로 매핑한다. 이렇게 얻어진 점 집합 P = {(i‑c, j‑c, a_{ij})} (c = (n‑1)/2)는 격자 중심을 기준으로 대칭성을 유지한다. 점들의 볼록 껍질 Conv(P)를 ‘마법 보석’이라 명명하고, 이 다면체의 형태가 마방진의 특성을 완전히 포착한다는 점이 핵심이다.

통계적 관점에서, 각 점의 2차원 위치 벡터 x = (i‑c, j‑c)와 값 스칼라 y = a_{ij} 사이의 공분산 Cov(x, y) = E

📄 논문 본문 발췌 (Translation)

...(본문 내용이 길어 생략되었습니다. 사이트에서 전문을 확인해 주세요.)