지속 라플라시안 도표
📝 원문 정보
- Title: Persistent Laplacian Diagrams
- ArXiv ID: 2512.05463
- 발행일: 2025-12-05
- 저자: Inkee Jung, Wonwoo Kang, Heehyun Park
📝 초록 (Abstract)
지속 호몰로지(PH)의 벡터화 방법인 퍼시스턴스 이미지(PI)는 안정성을 유지하면서 영속성 다이어그램을 유한 차원 벡터 공간으로 인코딩한다. 이와 병행하여 영속 라플라시안(PL)이 제안되었으며, 그 스펙트럼은 PH 정보를 포함함과 동시에 보다 풍부한 기하학적·조합적 특성을 담는다. 본 연구에서는 PL을 벡터화하기 위한 유사한 방법을 개발한다. PL을 실수값으로 매핑하는 서명을 도입하고, 이를 영속 라플라시안 도표(PLD)와 영속 라플라시안 이미지(PLI)로 구성한다. 우리는 PLI가 영속성 다이어그램의 잡음에 대해 안정함을 증명한다. 또한, PH와 조합 라플라시안 서명 모두로 구별되지 않는 그래프 예시들을 제시하고, PL 서명을 통해 이들을 효과적으로 구분함을 보여준다.💡 논문 핵심 해설 (Deep Analysis)
이에 반해 영속 라플라시안은 각 스케일에서 정의된 라플라시안 연산자의 스펙트럼을 이용한다. 라플라시안의 고유값은 그래프 혹은 셀 복합체의 연결성, 클러스터링, 확산 특성 등을 반영하므로, PH가 놓치는 미세 구조를 드러낼 수 있다. 논문은 이러한 PL의 풍부한 정보를 벡터 형태로 정형화하기 위해 두 단계의 서명(signature) 설계를 제안한다. 첫 번째 서명은 각 스케일 구간에서 라플라시안의 고유값 집합을 실수값 함수로 매핑하고, 두 번째 서명은 이 함수를 2차원 격자에 누적해 이미지 형태(PLI)로 변환한다. 이렇게 구성된 영속 라플라시안 도표(PLD)와 영속 라플라시안 이미지(PLI)는 기존 PI와 구조적으로 유사하면서도, 라플라시안 스펙트럼이 제공하는 추가적인 기하학적·조합적 정보를 내포한다.
안정성 측면에서 저자들은 PLI가 PD에 가해지는 작은 잡음(예: 점의 위치 변동)에도 불변임을 수학적으로 증명한다. 이는 기존 PI의 안정성 증명과 유사한 Lipschitz 연속성을 기반으로 하지만, 라플라시안 고유값이 연속적으로 변하는 특성을 정교히 다루어야 하는 복잡성을 포함한다. 증명 과정에서 사용된 핵심 아이디어는 라플라시안 스펙트럼이 셀 복합체의 체인 복소수 구조에 의존하므로, PD의 작은 변동이 해당 체인 복소수의 경계 연산자에 미치는 영향을 상한으로 제어할 수 있다는 점이다.
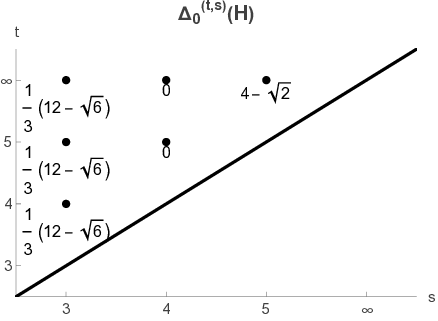
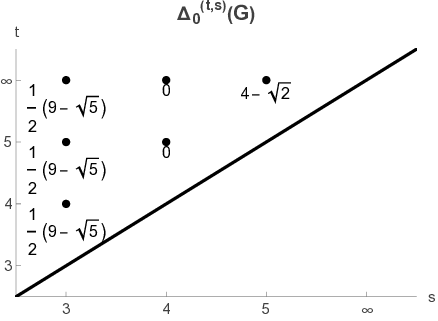
실험 부분에서는 두 개의 그래프를 설계한다. 이 그래프들은 동일한 영속 호몰로지 바코드와 조합 라플라시안(예: 정규 라플라시안) 서명에도 불구하고, PL 서명을 적용했을 때 서로 다른 스펙트럼을 보인다. 이는 PL이 단순히 위상적 ‘구멍’의 존재 여부를 넘어, 복합체 내부의 연결 패턴과 가중치 분포까지 감지한다는 강력한 증거이다. 이러한 사례는 PH와 기존 라플라시안 기반 특성만으로는 구분이 어려운 데이터에서 PL 기반 벡터화가 실질적인 차별성을 제공함을 시사한다.
전반적으로 이 연구는 TDA와 그래프 신호 처리의 교차점에서 새로운 데이터 표현 방식을 제시한다. 향후 연구에서는 PLD/PLI를 딥러닝 모델에 직접 입력하거나, 다른 위상적·스펙트럼 기반 서명과 결합해 멀티모달 특성 추출을 시도할 여지가 크다. 또한, 고차원 셀 복합체, 시계열 데이터, 혹은 노이즈가 심한 실세계 데이터셋에 대한 적용 가능성을 탐색함으로써, PL 기반 벡터화의 일반화 능력을 검증할 필요가 있다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리