다양한 AI 에이전트 전략을 위한 수학적 프레임워크
📝 원문 정보
- Title: Mathematical Framing for Different Agent Strategies
- ArXiv ID: 2512.04469
- 발행일: 2025-12-04
- 저자: Philip Stephens, Emmanuel Salawu
📝 초록 (Abstract)
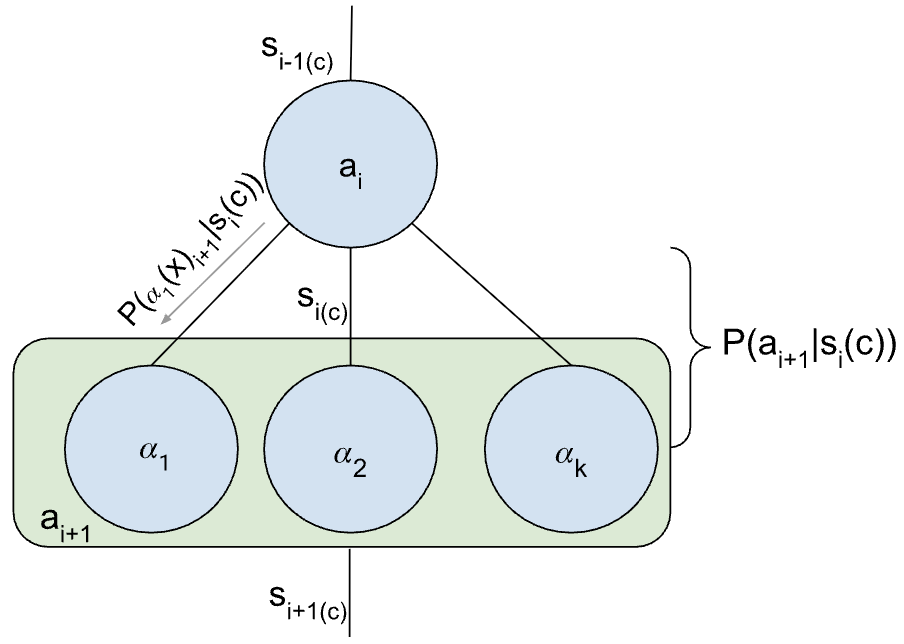
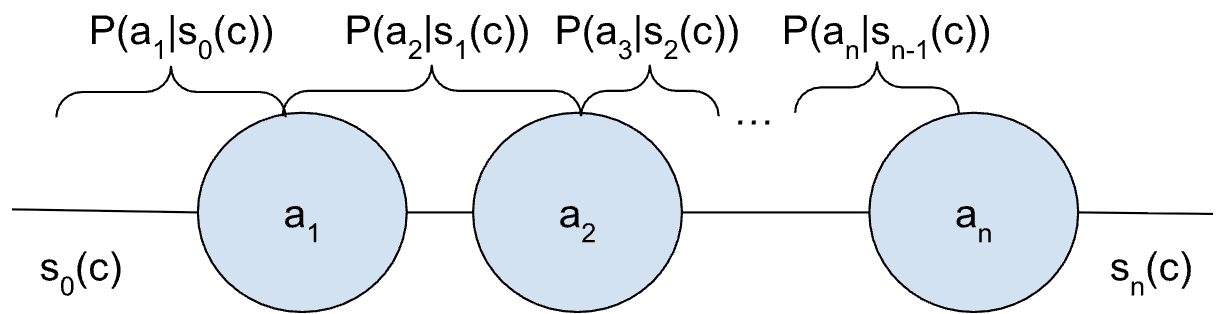
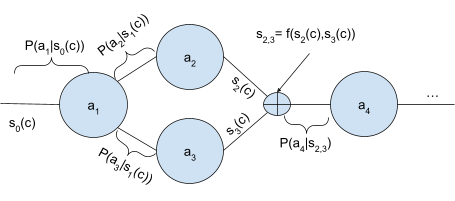
본 논문은 다양한 AI 에이전트 전략을 이해하고 비교하기 위한 통합 수학·확률론적 프레임워크를 제시한다. ReAct, 다중 에이전트 시스템, 제어 흐름과 같은 고수준 설계 개념을 엄밀한 수학적 형식과 연결함으로써, 에이전트의 작동 과정을 확률 연쇄(chain of probabilities)로 모델링한다. 이를 통해 각 전략이 목표 달성을 위해 어떻게 확률을 조작하는지 상세히 분석할 수 있다. 또한 본 연구는 각 접근법이 보유한 최적화 가능한 레버를 직관적으로 구분하는 “자유도(Degrees of Freedom)” 개념을 도입하여, 과제 특성에 맞는 전략 선택을 안내한다. 궁극적으로 복잡한 에이전트 시스템 내에서 성공 확률을 극대화하기 위한 설계·평가 기준을 명확히 제시한다.💡 논문 핵심 해설 (Deep Analysis)
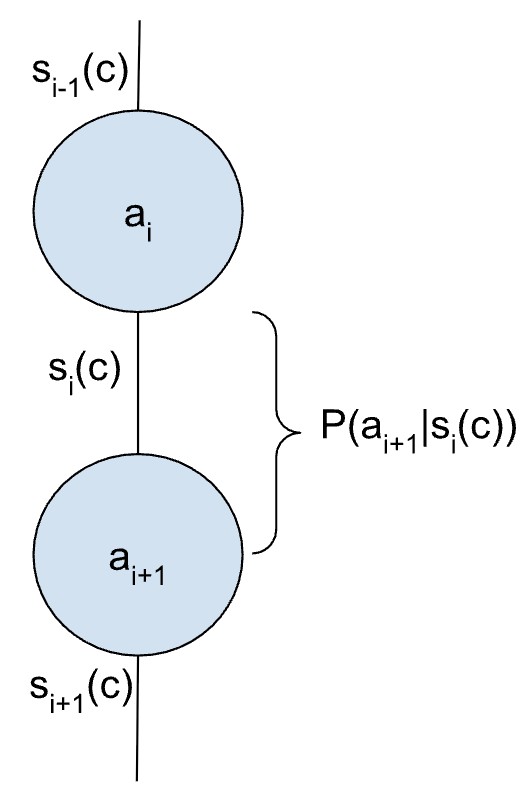
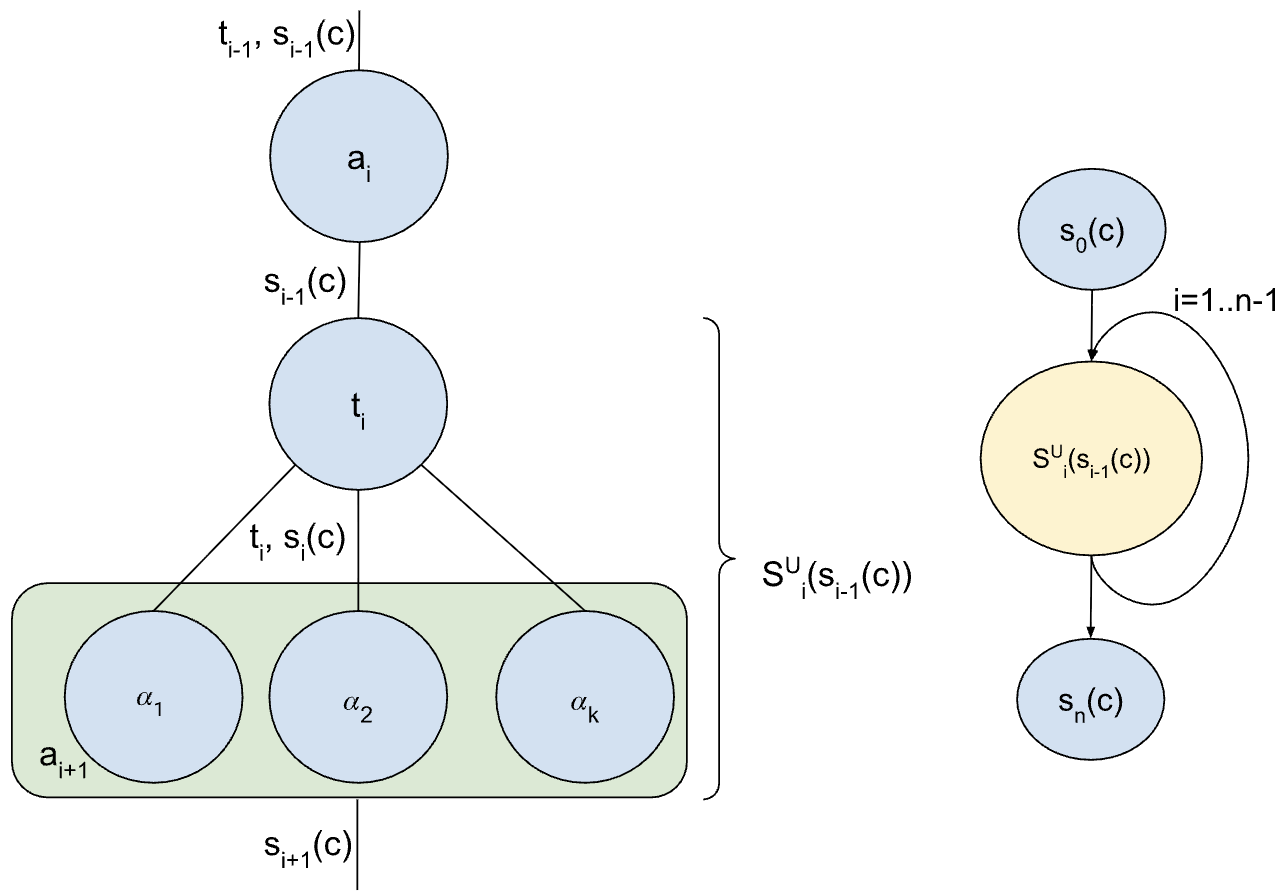
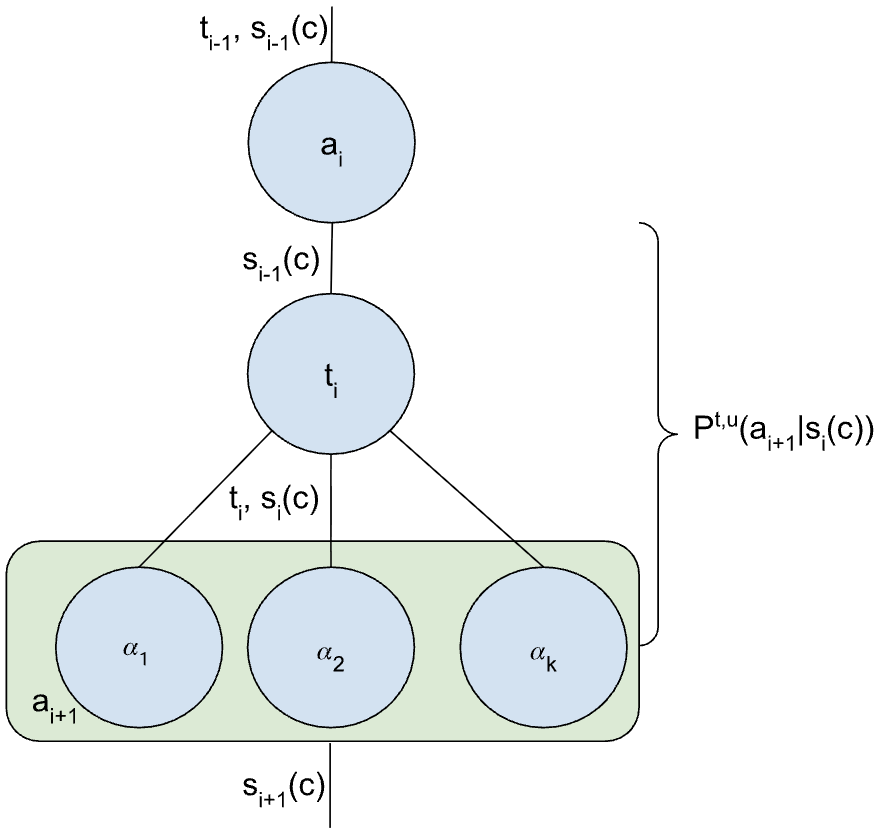
특히 “자유도(Degrees of Freedom)” 개념은 전략 선택에 실용적인 가이드라인을 제공한다. 예를 들어, ReAct는 내부 사고(Thought)와 외부 행동(Action) 사이의 전이 확률을 조정하는 자유도가 크지만, 외부 환경 피드백을 직접 활용하는 정도는 제한적이다. 반면 다중 에이전트 시스템은 각 에이전트 간 통신 프로토콜, 협업/경쟁 메커니즘, 그리고 전역 목표에 대한 공유 확률 분포 등 다층적인 자유도를 갖는다. 제어 흐름 기반 에이전트는 루프 구조와 조건부 분기점에서의 확률 선택을 최적화함으로써, 실시간 제어 요구에 특화된 자유도를 제공한다. 이러한 자유도의 차이를 정량화하면, 특정 작업(예: 복합 의사결정, 실시간 로봇 제어, 대규모 정보 탐색)에서 어느 전략이 비용 효율적으로 성공 확률을 높일 수 있는지 사전에 예측할 수 있다.
또한 확률 연쇄 모델은 학습과 추론을 동일한 수식 체계 안에 포함시켜, 강화학습, 베이지안 추론, 혹은 심층 생성 모델 등 다양한 학습 패러다임을 자연스럽게 연결한다. 이는 향후 “하이브리드 에이전트” 설계—예를 들어, ReAct의 사고 모듈에 베이지안 업데이트를 결합하거나, 다중 에이전트 시스템에 강화학습 기반 정책 조정을 삽입하는 경우—에 대한 이론적 기반을 제공한다.
하지만 몇 가지 한계도 존재한다. 확률 연쇄를 실제 구현에 옮기려면 각 전이 확률을 정확히 추정해야 하는데, 복잡한 현실 환경에서는 데이터 부족이나 비정상성으로 인해 추정 오차가 크게 발생할 수 있다. 또한 자유도의 정의가 다소 추상적이어서, 실제 시스템 설계 시 구체적인 매트릭스로 전환하는 과정이 필요하다. 향후 연구에서는 경험적 베이스라인을 구축하고, 자유도와 성능 사이의 정량적 관계를 실험적으로 검증하는 작업이 요구된다.
요약하면, 이 논문은 AI 에이전트 설계에 대한 공통 언어를 제공함으로써, 전략 간 비교와 선택을 보다 과학적으로 수행할 수 있게 만든다. 확률 연쇄와 자유도라는 두 축을 중심으로 한 프레임워크는 학계·산업 모두에서 복합적인 에이전트 시스템을 설계·평가하는 새로운 패러다임을 제시한다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리