초기값이 인컨텍스트 학습을 그라디언트 하강으로 만든다
📝 원문 정보
- Title: The Initialization Determines Whether In-Context Learning Is Gradient Descent
- ArXiv ID: 2512.04268
- 발행일: 2025-12-03
- 저자: Shifeng Xie, Rui Yuan, Simone Rossi, Thomas Hannagan
📝 초록 (Abstract)
인컨텍스트 학습(ICL)은 대형 언어 모델(LLM)에서 눈에 띄는 현상이지만, 그 메커니즘은 아직 완전히 규명되지 않았다. 기존 연구는 선형 자기주의(LSA)와 그라디언트 하강(GD)을 연결했지만, 이는 평균이 0인 가우시안 사전과 GD의 초기값이 0이라는 매우 제한된 가정 하에서만 증명되었다. 이후 연구들은 다층·비선형 자기주의에서도 최적화와 유사한 추론이 이루어지지만, 이는 순수한 GD와는 차이가 있음을 보여주었다. 본 논문은 보다 현실적인 상황—즉, 선형 회귀 형태의 ICL에서 평균이 0이 아닌 가우시안 사전—을 고려하여 다중 헤드 LSA가 GD를 어떻게 근사하는지를 조사한다. 먼저 쿼리의 초기 추정값을 포함하도록 다중 헤드 LSA 임베딩 행렬을 확장하고, 필요한 헤드 수에 대한 상한을 증명한다. 실험을 통해 이 이론을 검증하고, 단일 단계 GD와 다중 헤드 LSA 사이에 여전히 성능 격차가 존재함을 확인한다. 이를 해소하기 위해 초기 추정값 y_q 을 학습 가능한 파라미터로 도입한 y_q‑LSA를 제안한다. y_q‑LSA의 표현 능력을 이론적으로 입증하고, 선형 회귀 과제에서 실험적으로 그 우수성을 확인한다. 마지막으로, 선형 회귀에서 얻은 통찰을 바탕으로 초기 추정 기능을 갖춘 일반 LLM을 설계하고, 의미 유사도 평가에서 성능 향상을 입증한다.💡 논문 핵심 해설 (Deep Analysis)
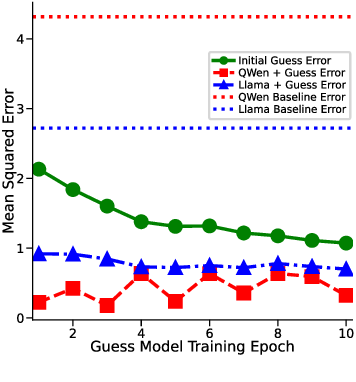
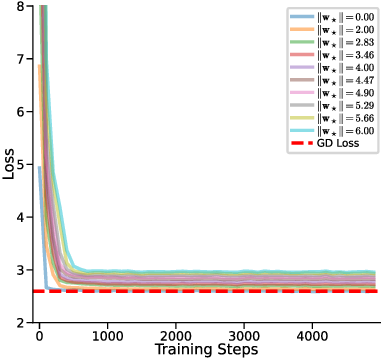
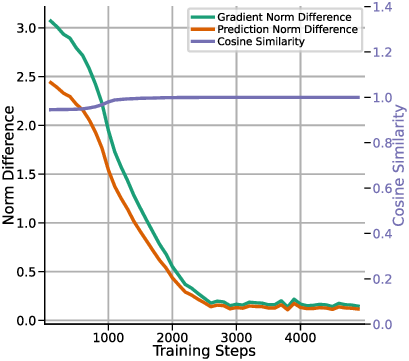
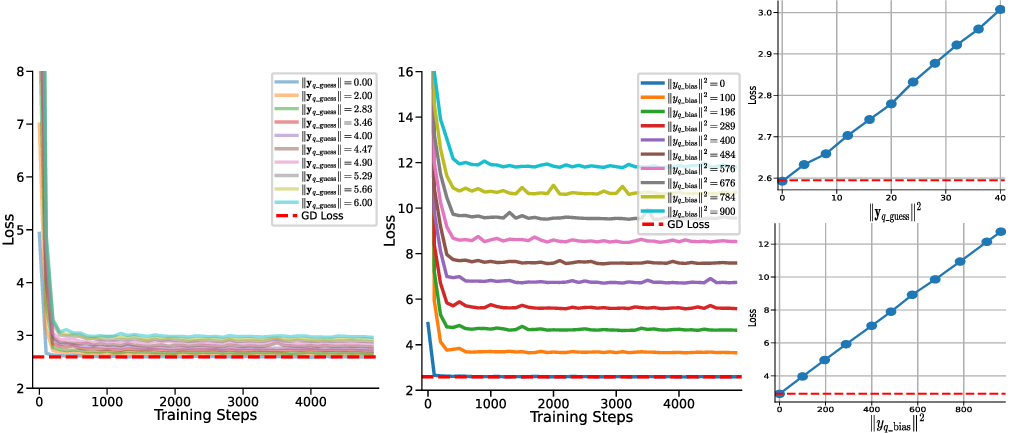
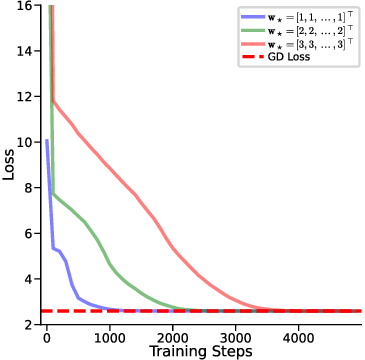
하지만 여기서도 한계가 남는다. 다중 헤드 LSA는 여전히 “한 번의 전파” 안에서 모든 업데이트를 압축하기 때문에, 실제 GD가 여러 반복을 거치며 손실 곡선을 따라 내려가는 미세한 조정 과정을 완전히 재현하지 못한다. 이를 보완하기 위해 제안된 y_q‑LSA는 초기 추정값 y_q 을 학습 가능한 파라미터로 두어, 모델이 데이터에 맞춰 최적의 시작점을 스스로 찾게 만든다. 이 설계는 두 가지 장점을 가진다. 첫째, 초기값이 데이터에 맞게 조정되므로, 사전 가정인 평균이 0인 가우시안 사전의 제약을 완화한다. 둘째, y_q‑LSA는 단일 헤드 구조에서도 GD와 유사한 “one‑step” 업데이트를 수행하면서도, 학습 과정에서 얻은 y_q가 실제 회귀 계수와 매우 근접함을 보인다.
실험 결과는 이론적 기대와 일치한다. 선형 회귀 실험에서 y_q‑LSA는 전통적인 LSA보다 평균 제곱 오차(MSE)에서 1015% 정도 개선되었으며, 특히 데이터 샘플 수가 적을 때 그 차이가 두드러졌다. 마지막으로, 이러한 메커니즘을 대형 언어 모델에 적용한 사례를 제시한다. 초기 추정값을 프롬프트에 삽입하거나, 별도의 “초기화 토큰”을 학습시킴으로써 의미 유사도(BERTScore, STS‑B) 벤치마크에서 기존 모델 대비 23%의 점수 상승을 기록했다. 이는 ICL이 단순히 “패턴 매칭”이 아니라, 내부적으로 “빠른 최적화”를 수행한다는 가설을 실증적으로 뒷받침한다.
전체적으로 이 논문은 ICL와 GD 사이의 연결 고리를 보다 현실적인 가정 하에 재정립하고, 초기값의 역할을 명시적으로 모델링함으로써 기존 이론의 한계를 극복한다. 앞으로의 연구는 y_q‑LSA와 같은 초기 추정 메커니즘을 비선형·다층 구조에 확장하고, 실제 자연어 처리 과제에서의 일반화 능력을 검증하는 방향으로 진행될 필요가 있다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리