네비게이션에서 정교화까지 흐름 기반 확산 모델의 두 단계 특성을 오라클 속도로 밝히다
📝 원문 정보
- Title: From Navigation to Refinement: Revealing the Two-Stage Nature of Flow-based Diffusion Models through Oracle Velocity
- ArXiv ID: 2512.02826
- 발행일: 2025-12-02
- 저자: Haoming Liu, Jinnuo Liu, Yanhao Li, Liuyang Bai, Yunkai Ji, Yuanhe Guo, Shenji Wan, Hongyi Wen
📝 초록 (Abstract)
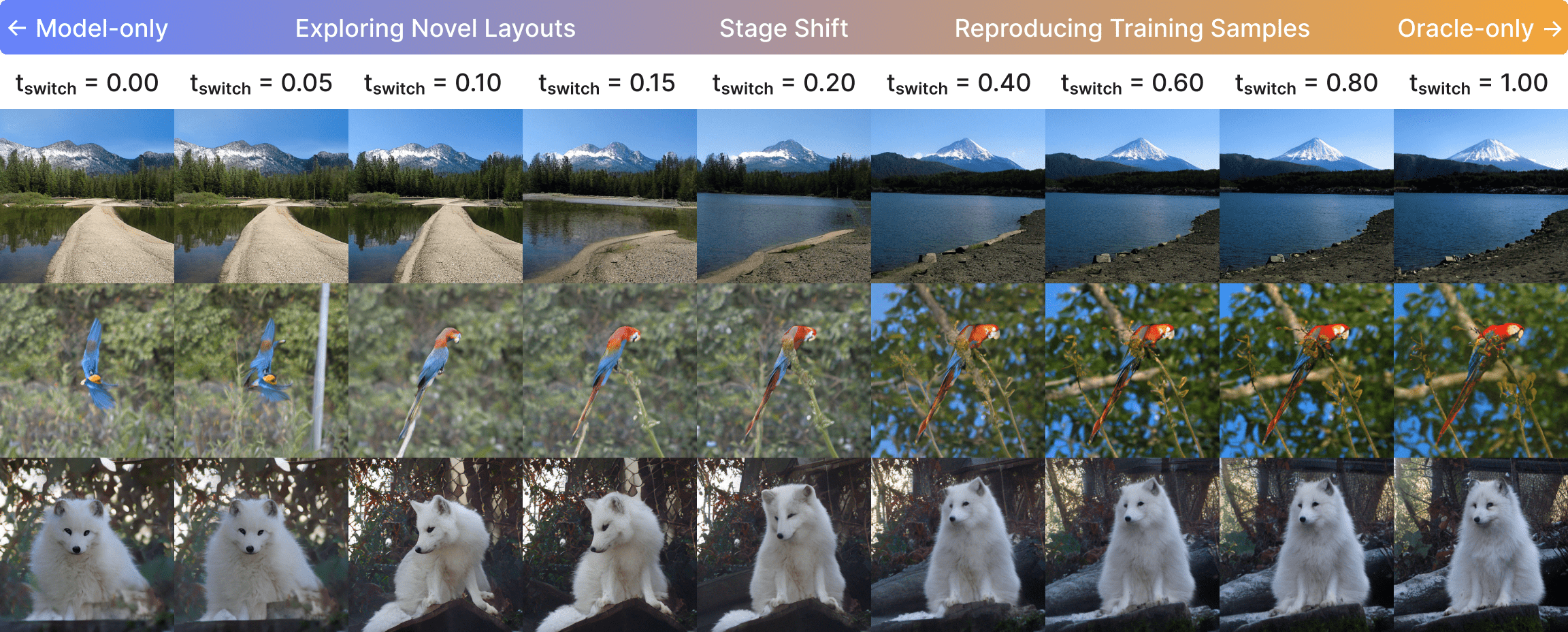
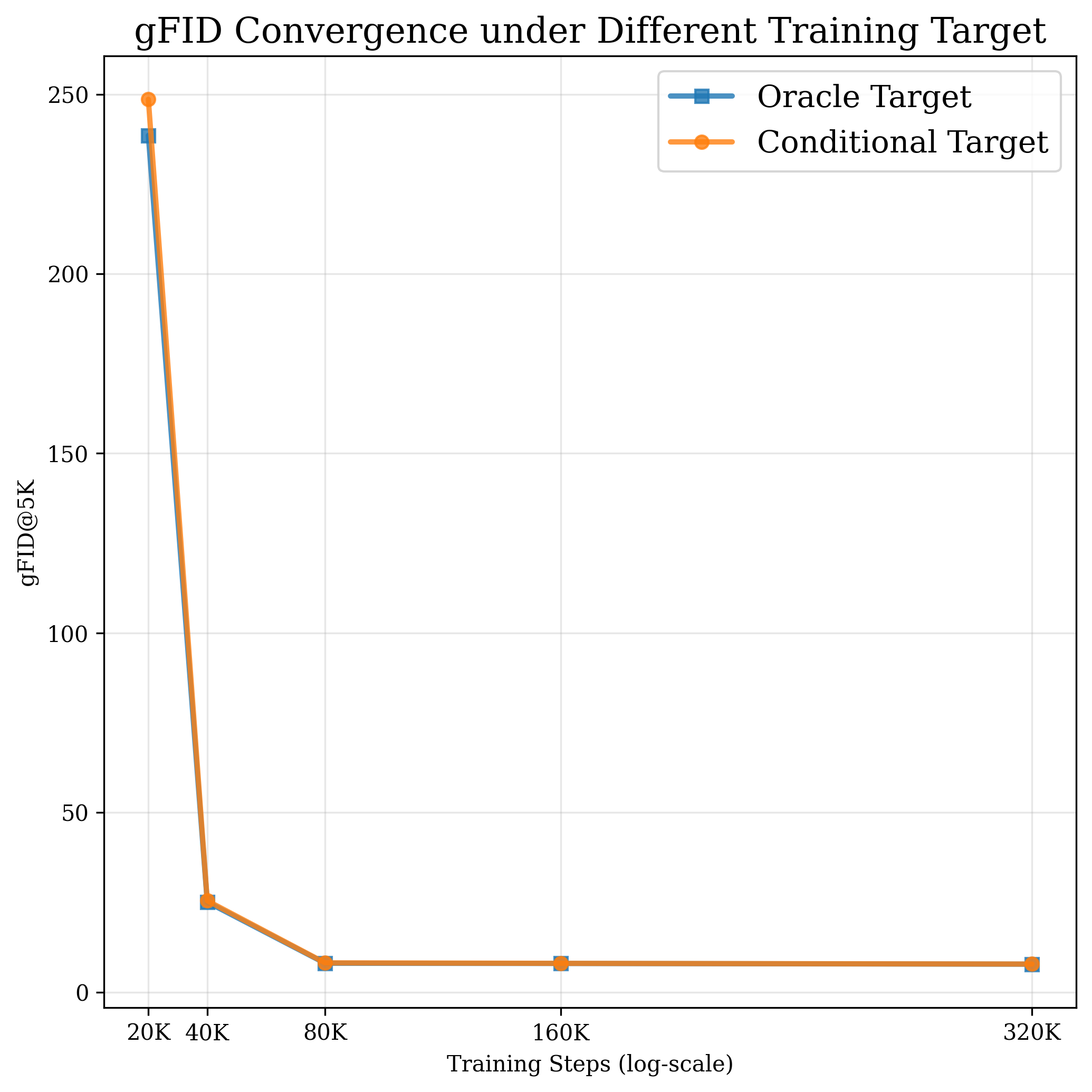
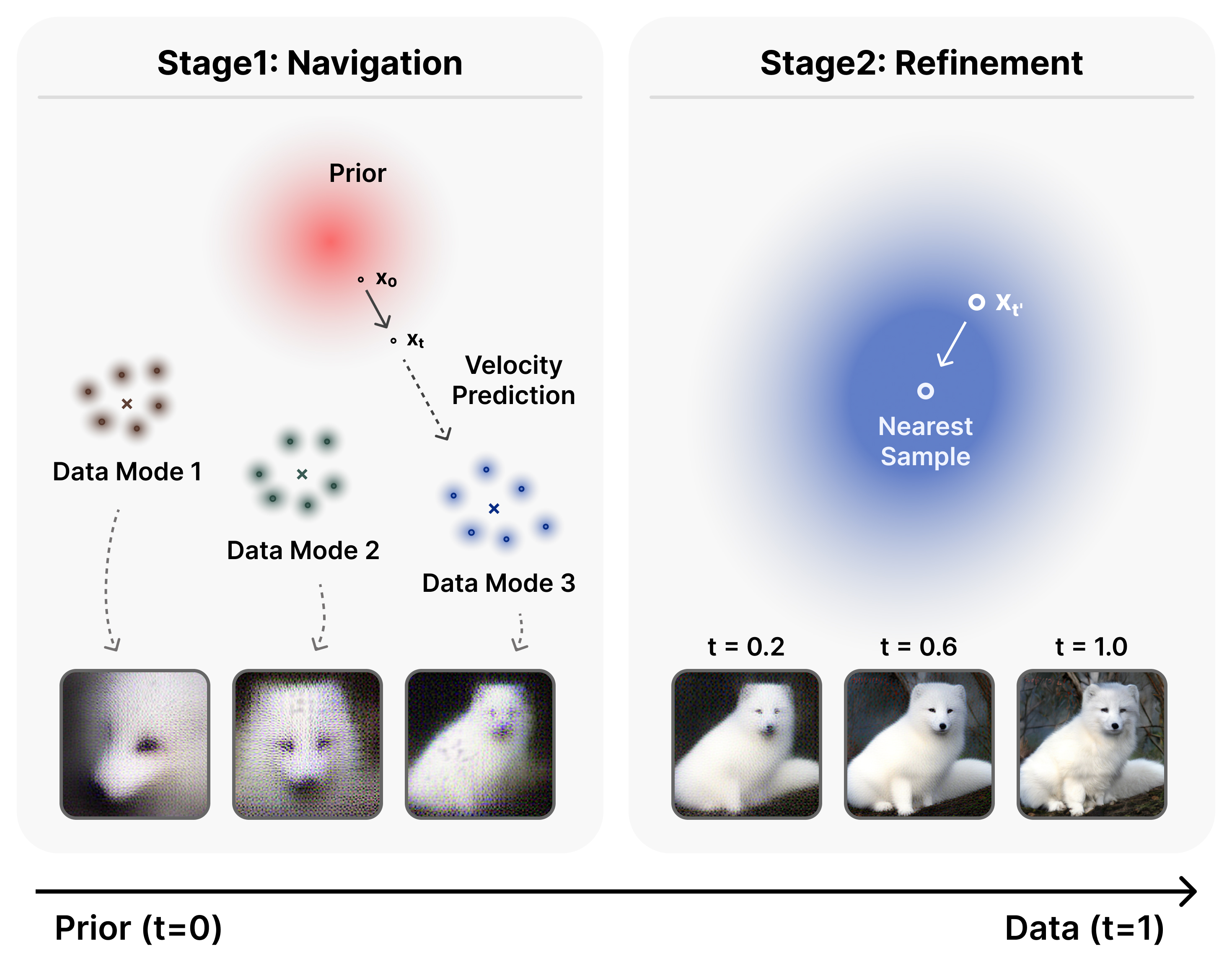
흐름 기반 확산 모델은 이미지와 비디오 생성 분야에서 최신 패러다임으로 부상했지만, 이들의 기억‑일반화 메커니즘은 아직 충분히 규명되지 않았다. 본 연구에서는 흐름 매칭(FM) 목표를 재검토하고, 폐쇄형 해를 갖는 주변 속도 필드를 분석한다. 이를 통해 오라클 FM 타깃을 정확히 계산할 수 있다. 오라클 속도 필드를 살펴보면, 흐름 기반 확산 모델이 본질적으로 두 단계 학습 목표를 갖는다는 것이 드러난다: 초기 단계에서는 데이터 모드들의 혼합에 의해 안내되고, 후반 단계에서는 가장 가까운 데이터 샘플이 지배한다. 이러한 두 단계 목표는 학습 행동을 구분한다. 초기 ‘네비게이션’ 단계에서는 전역적인 레이아웃을 형성하며 데이터 모드 간 일반화를 수행하고, 후반 ‘정교화’ 단계에서는 세부 정보를 점점 더 기억한다. 이 통찰을 바탕으로 타임스텝 이동 스케줄, 클래스‑프리 가이드(interval) 설계, 잠재 공간 구조 선택 등 실용적인 기법들의 효과를 설명한다. 본 연구는 확산 모델 훈련 역학에 대한 이해를 심화시키고, 향후 아키텍처 및 알고리즘 설계에 대한 원칙을 제시한다.💡 논문 핵심 해설 (Deep Analysis)

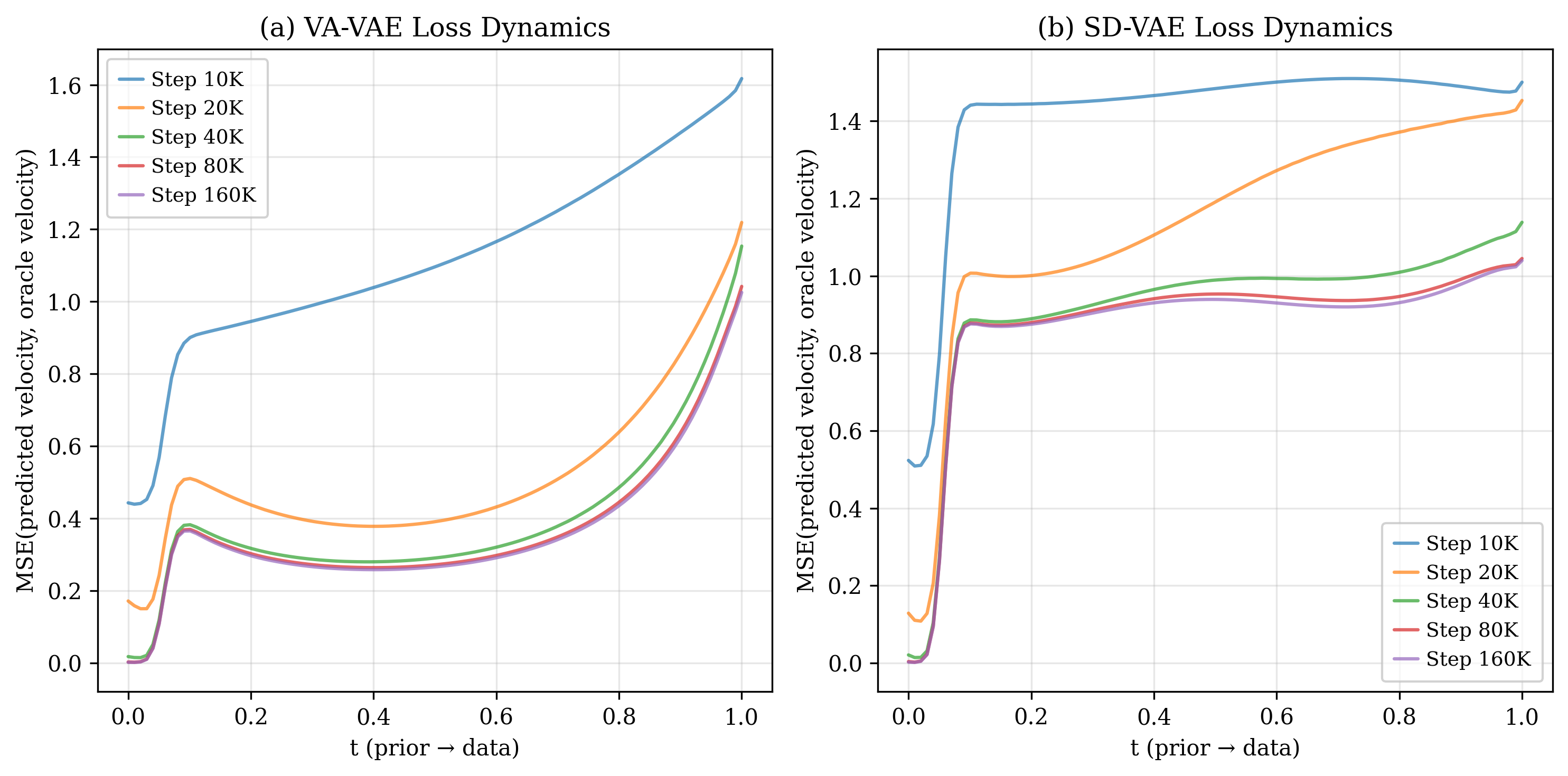
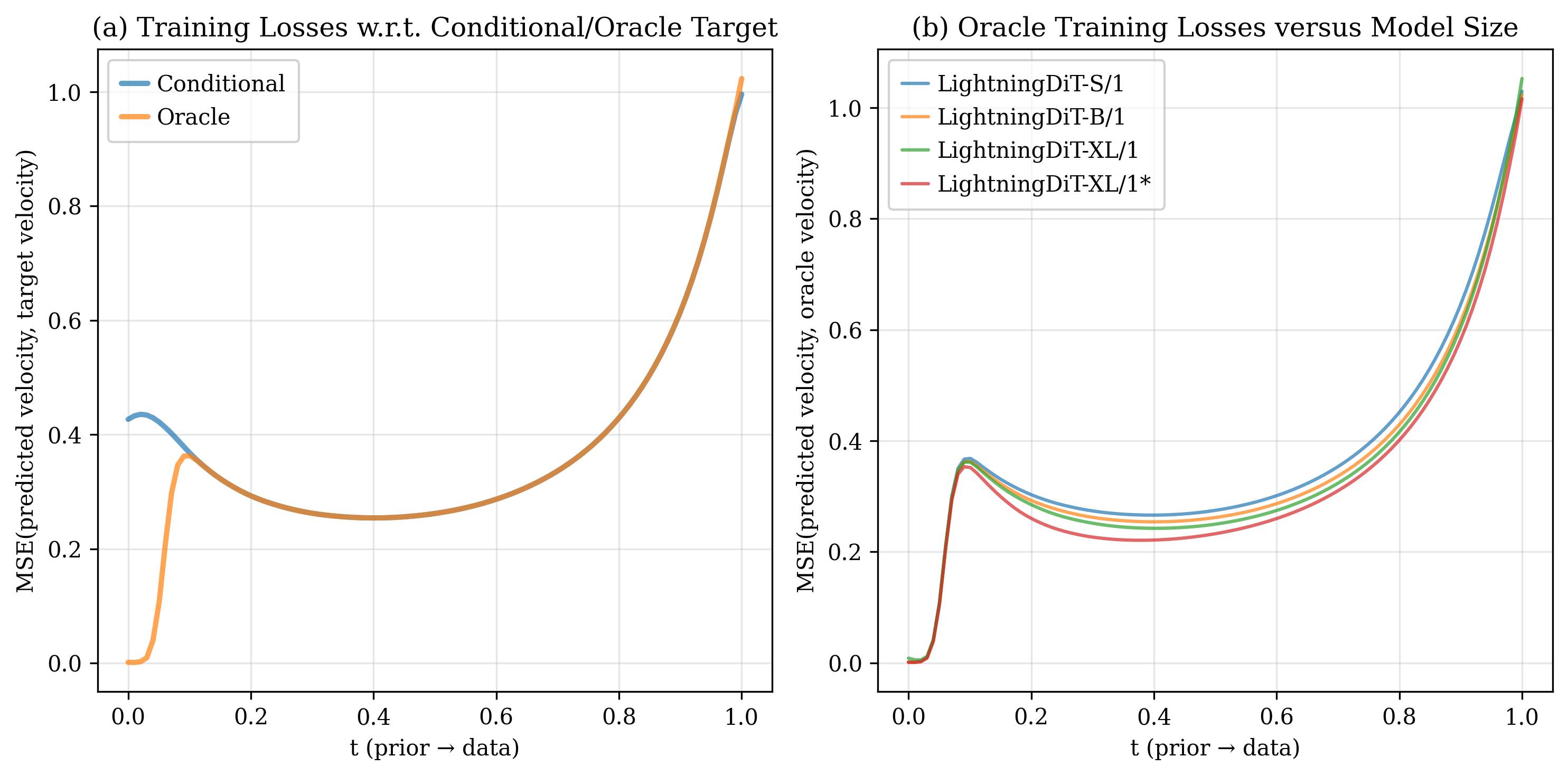
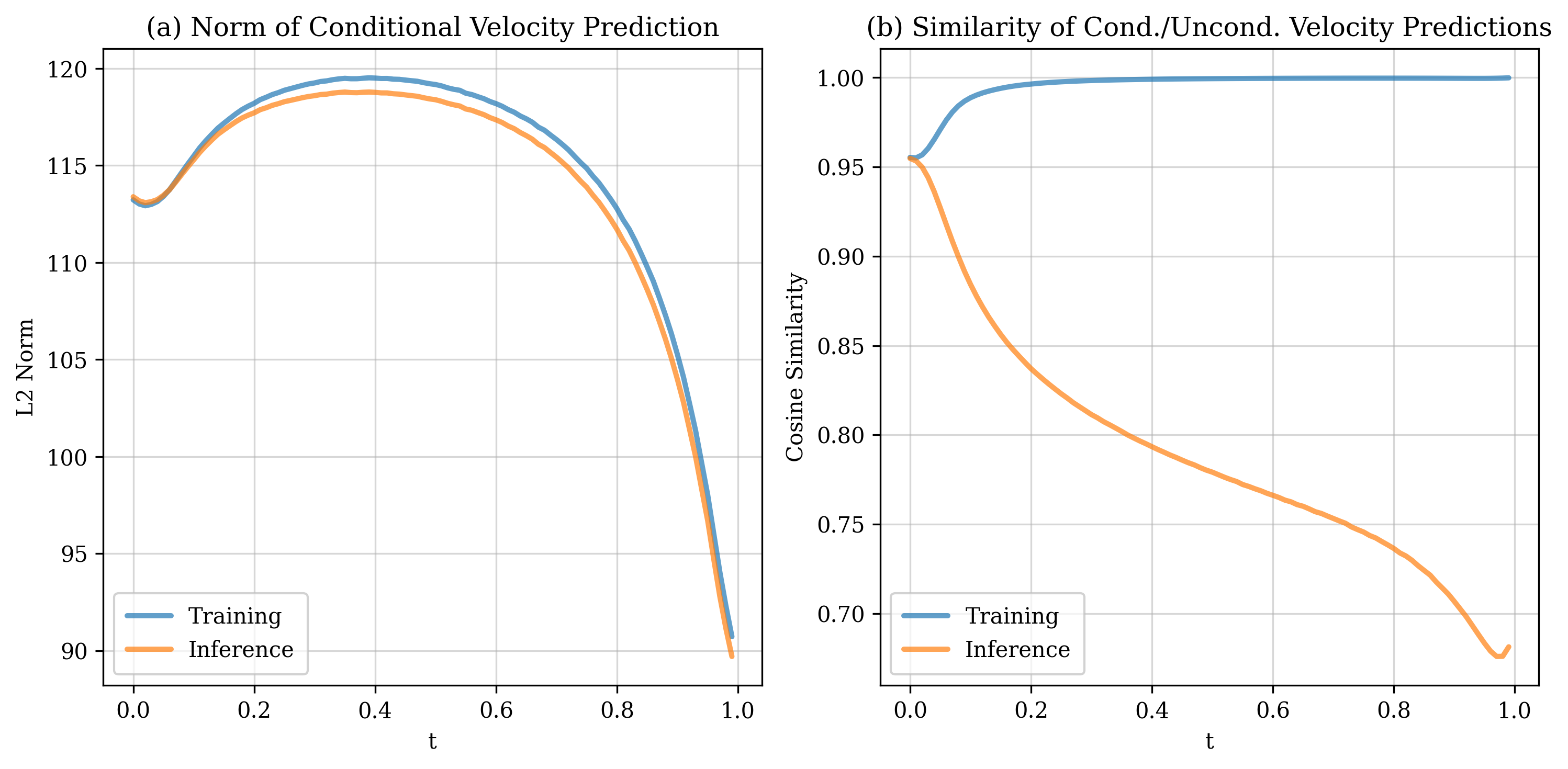
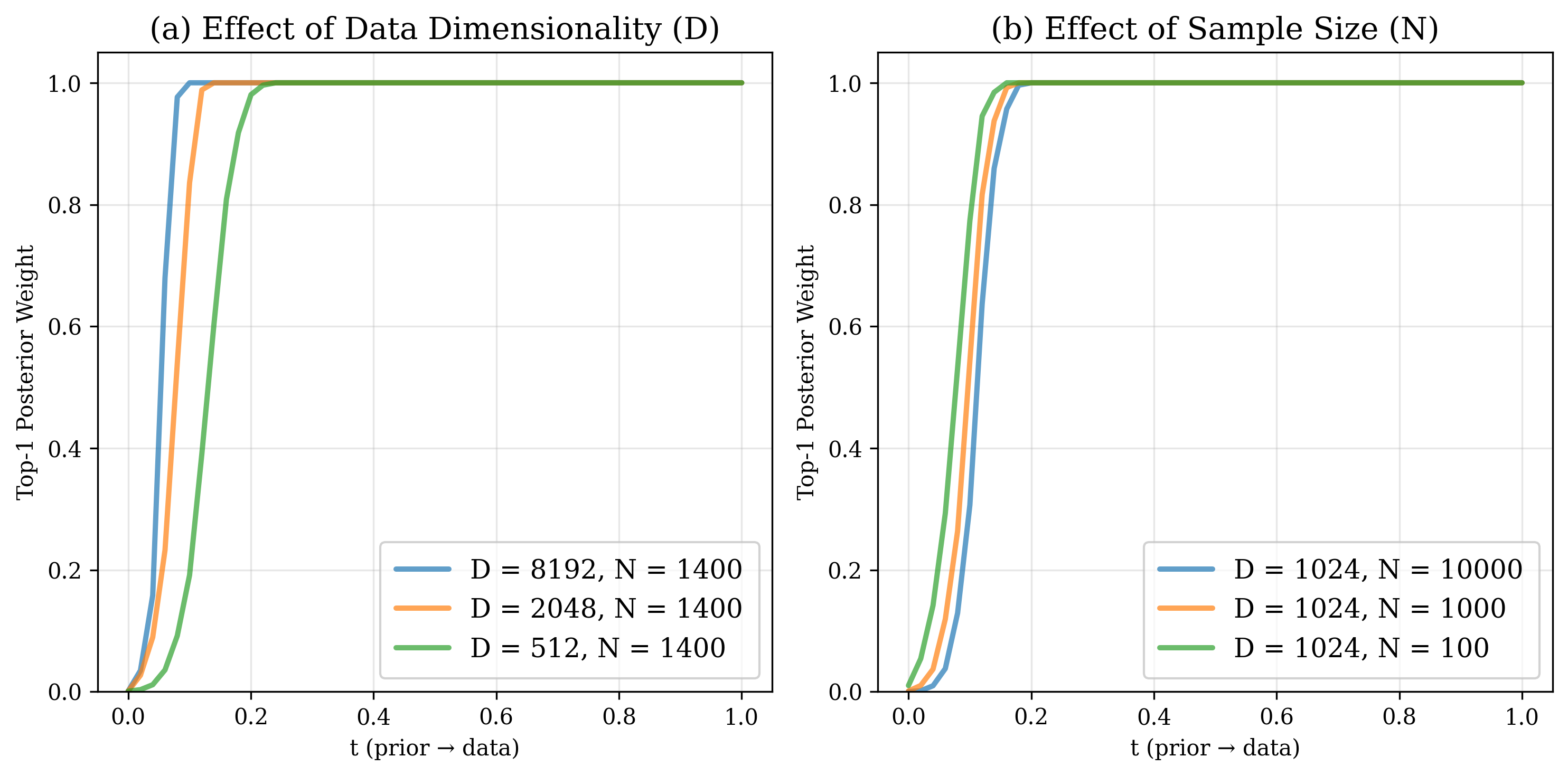
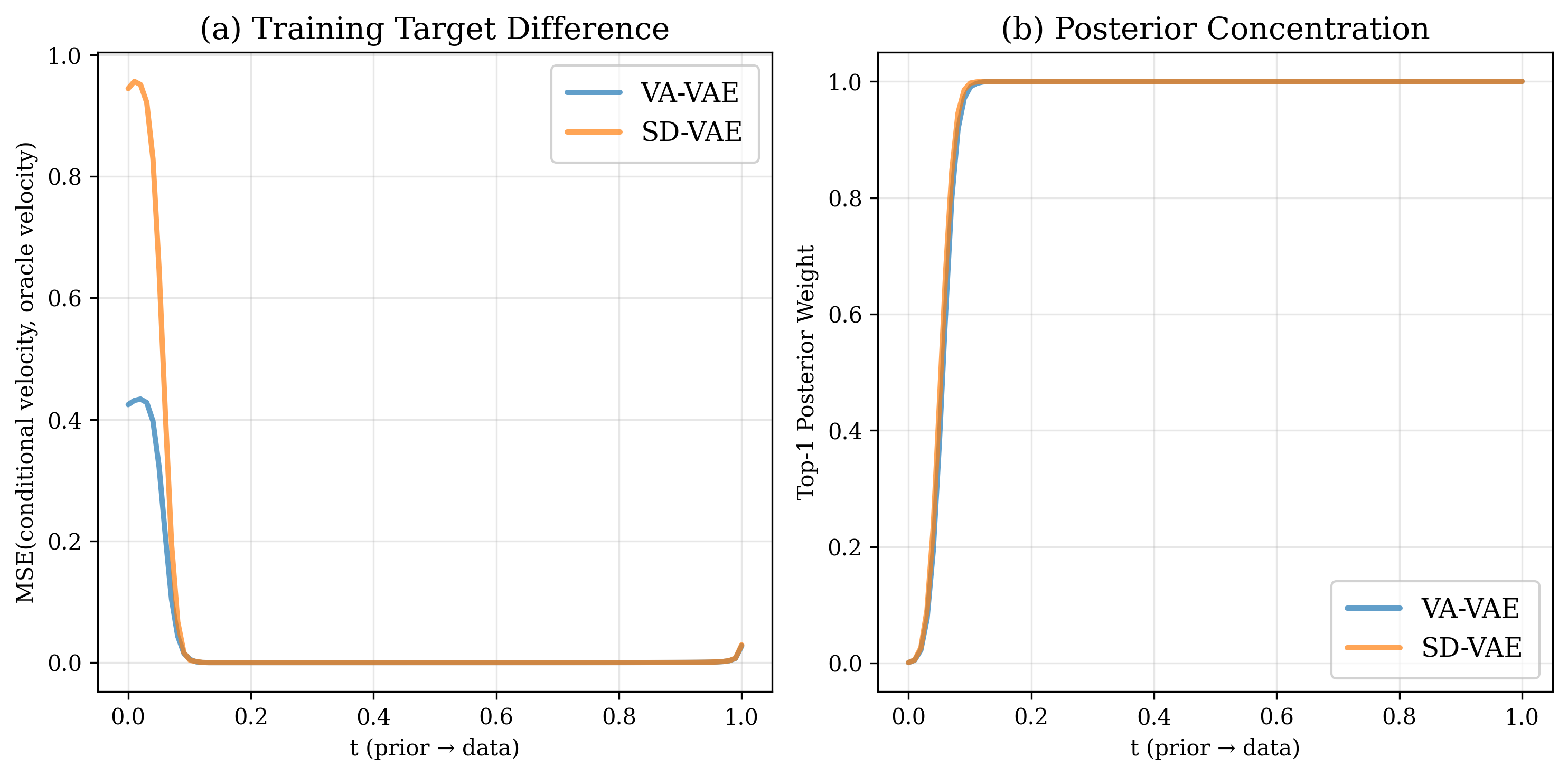
이 오라클 속도장을 시각화하고 수학적으로 분석한 결과, 두 가지 뚜렷한 구간이 존재한다는 것이 밝혀졌다. 초기 구간(작은 t)에서는 속도장이 여러 데이터 모드의 평균적인 방향을 가리키며, 이는 모델이 전역적인 구조—예를 들어 이미지의 대략적인 형태나 배경—를 빠르게 ‘네비게이션’하도록 만든다. 이 단계에서는 개별 샘플의 미세한 차이보다 모드 간 거리와 분포의 전반적인 형태가 학습에 더 큰 영향을 미친다.
반면 t가 커짐에 따라 속도장은 점점 특정 데이터 포인트, 즉 가장 가까운 실제 샘플을 가리키는 방향으로 수렴한다. 이는 ‘정교화(refinement)’ 단계로, 모델이 이미 형성된 전역 레이아웃 위에 미세한 텍스처, 색상, 세부 구조 등을 정확히 복제하려는 메커니즘이다. 이 단계에서 모델은 기억(memory) 성향이 강해지며, 과적합 위험도 동시에 증가한다.
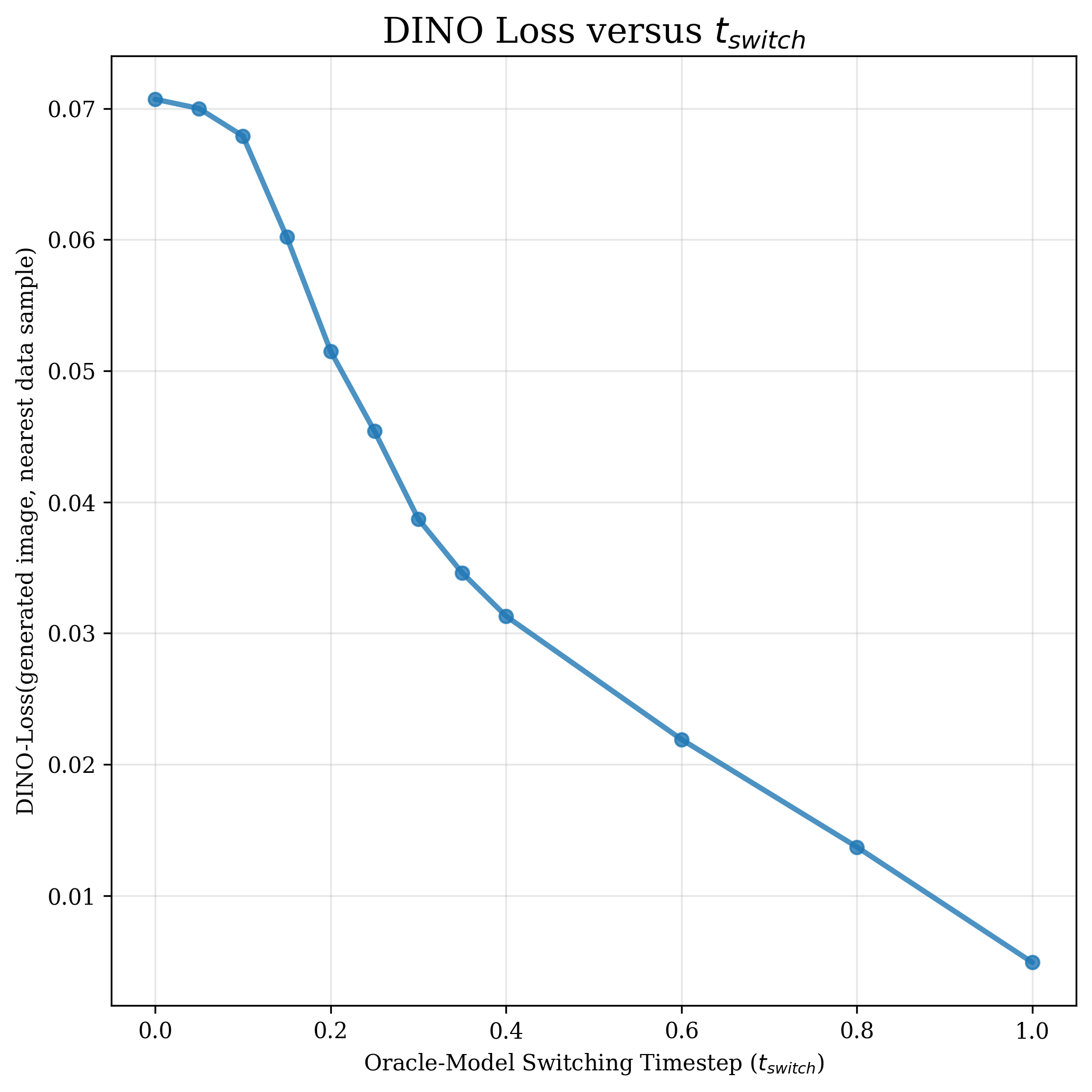
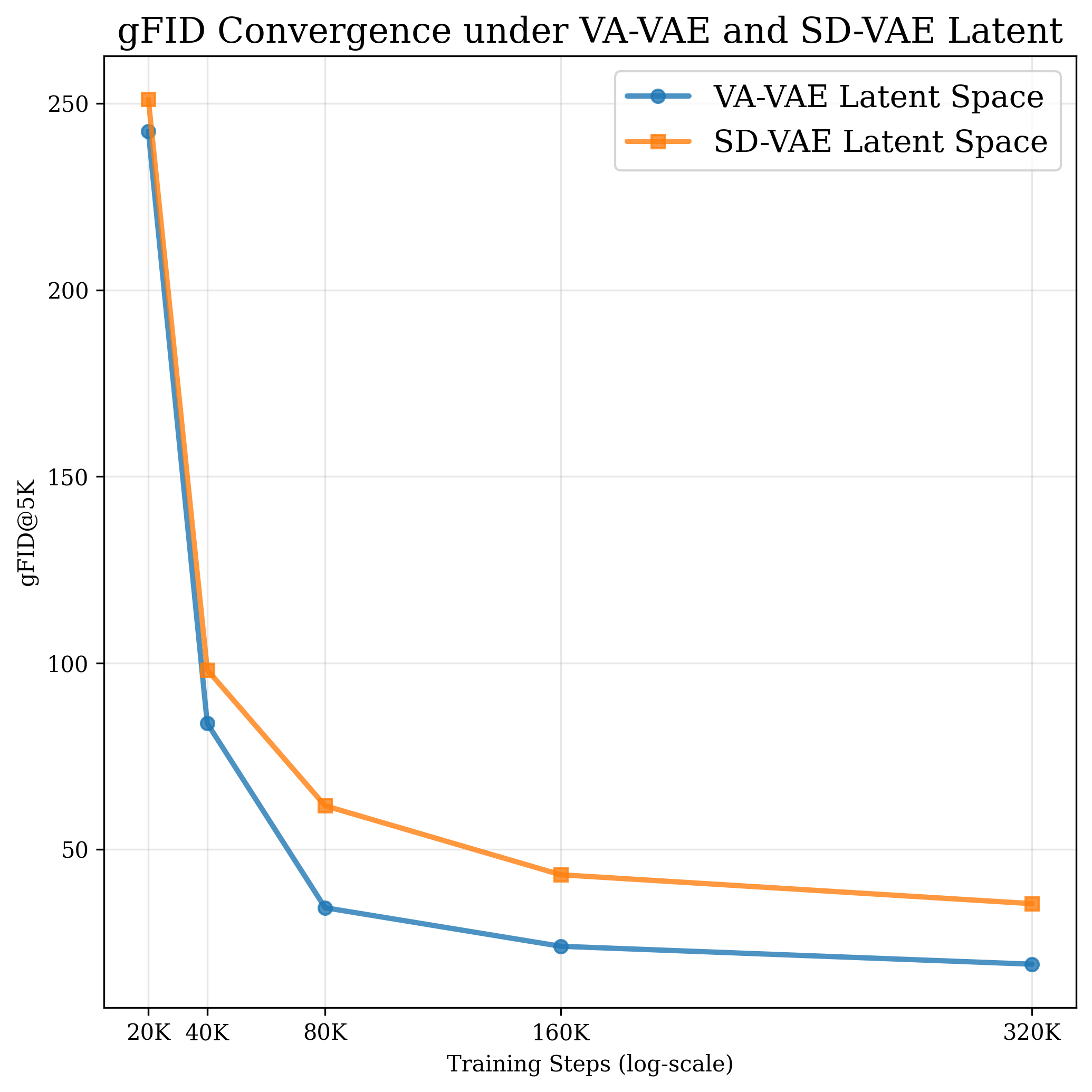
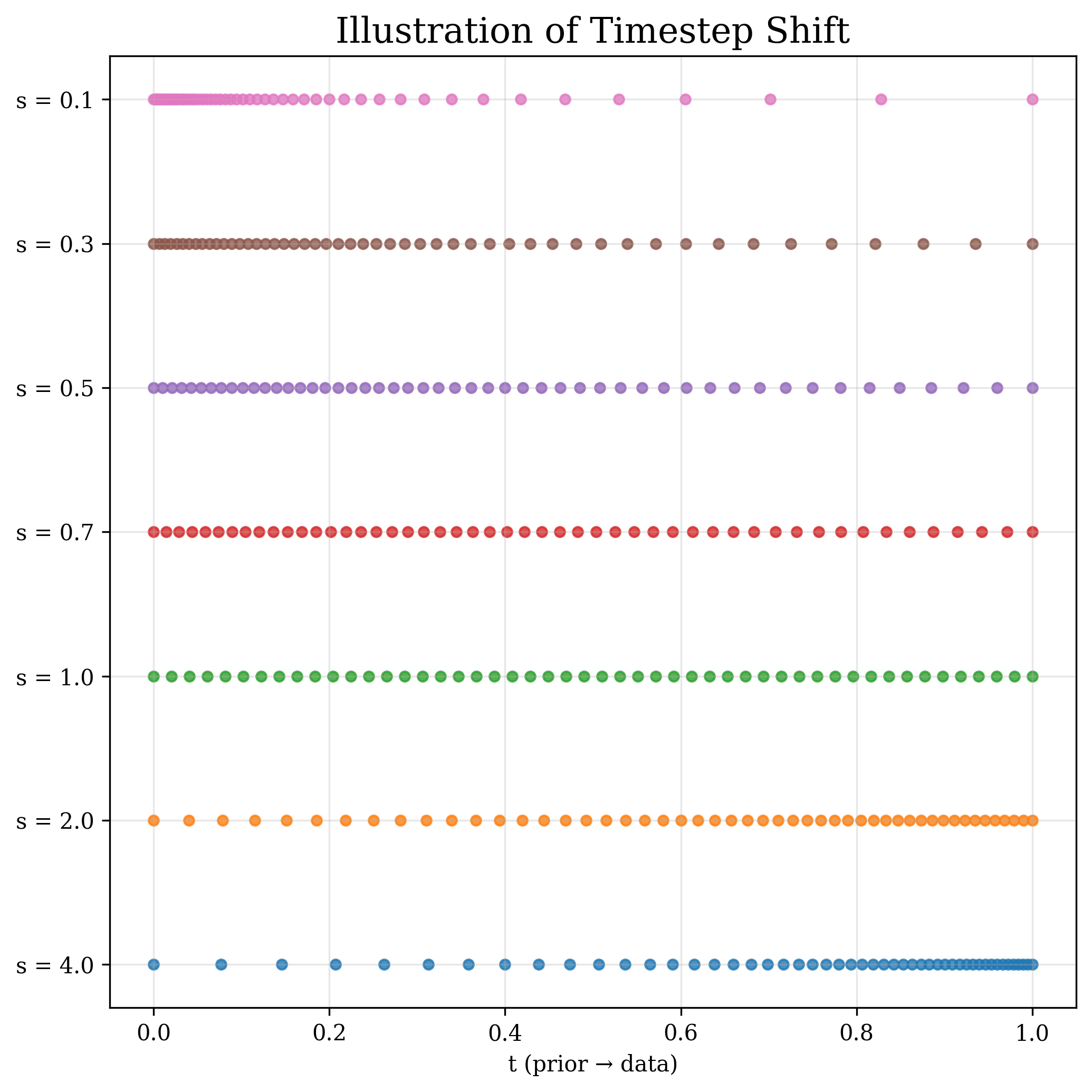
두 단계의 존재는 여러 실무 기법을 자연스럽게 설명한다. 첫째, 타임스텝‑시프트 스케줄은 초기 단계에서 더 큰 스텝을 사용해 빠른 전역 탐색을 촉진하고, 후반부에서는 작은 스텝으로 정교화를 강화한다는 설계 원칙과 일치한다. 둘째, 클래스‑프리 가이드(classifier‑free guidance)의 적용 구간을 조절하면, 초기 단계에서는 가이드를 최소화해 다양성을 확보하고, 정교화 단계에서만 가이드를 강화해 샘플 품질을 높일 수 있다. 셋째, 잠재 공간 설계—예를 들어 고차원 라티스 구조를 도입하거나, 데이터 모드 간 거리를 늘리는 변형—는 초기 네비게이션 단계에서 더 명확한 모드 구분을 가능하게 하여 전반적인 일반화 능력을 향상시킨다.
이러한 통찰은 향후 연구 방향에도 시사점을 제공한다. 예를 들어, 두 단계의 손실을 별도로 가중치 조정하거나, 동적 타임스텝 스케줄링을 통해 메모리와 일반화 사이의 트레이드오프를 자동으로 최적화하는 방법을 고안할 수 있다. 또한, 오라클 속도장을 활용한 ‘교사‑학생’ 프레임워크를 도입하면, 학생 모델이 초기 단계에서는 모드‑레벨 일반화를, 후반부에서는 오라클‑레벨 정밀 복제를 학습하도록 유도할 수 있다. 전반적으로 이 논문은 흐름 기반 확산 모델을 단순히 ‘노이즈를 제거하는 과정’이 아닌, 데이터 모드 탐색과 세부 복제라는 두 단계적 목표를 동시에 수행하는 복합 시스템으로 재해석함으로써, 이 분야의 이론적 기반을 크게 확장시켰다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리