정렬된 커버링 문제의 NP완전성 증명
📝 원문 정보
- Title: On the Complexity of the Ordered Covering Problem in Distance Geometry
- ArXiv ID: 2512.03124
- 발행일: 2025-12-02
- 저자: Michael Souza, Júlio Araújo, John Kesley Costa, Carlile Lavor
📝 초록 (Abstract)
정렬된 커버링 문제(OCP)는 이산화 가능한 분자 거리 기하학 문제(DMDGP)와 연관되어 있으며, 여기서 가지치기(edge pruning) 에지의 순서는 단백질 구조 결정에 사용되는 SBBU 알고리즘의 성능에 큰 영향을 미친다. 최근 Souza 등(2023)은 OCP를 순서가 지정된 지수 비용을 갖는 초그래프 커버링 문제로 공식화하고, 원래 SBBU 순서보다 수배에서 수천 배 빠른 성능을 보이는 탐욕적 휴리스틱을 제안하였다. 그러나 최적 해를 찾는 계산 복잡도는 여전히 미해결이었다. 본 논문에서는 강하게 NP‑완전한 3‑Partition 문제로부터 다항식 시간 감소를 구성함으로써 OCP가 NP‑complete임을 증명한다. 우리의 감소는 예산을 엄격히 제한하여 최적 해가 정확히 유효한 3‑Partition에 대응하도록 만든다. 이 결과는 최적 에지 순서를 찾는 데 존재하는 계산적 장벽을 명확히 하며, 현재 실무에서 사용되는 휴리스틱 접근법에 대한 이론적 정당성을 제공한다.💡 논문 핵심 해설 (Deep Analysis)
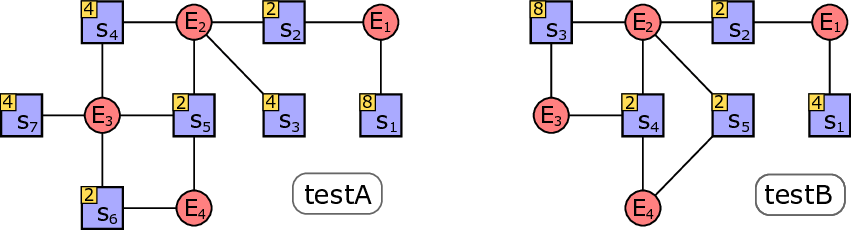
Souza 등(2023)은 OCP를 초그래프(하이퍼그래프) 커버링 문제로 모델링하였다. 여기서 각 하이퍼엣지는 하나 이상의 프루닝 에지를 포함하고, 각 하이퍼엣지에 부여된 비용은 선택 순서에 따라 지수적으로 증가한다는 특성을 가진다. 이 모델을 기반으로 제안된 탐욕적 휴리스틱은 현재까지 알려진 모든 실험 데이터에서 기존 SBBU 순서보다 수십 배에서 수천 배 빠른 성능을 보였으며, 특히 대규모 단백질(수천 개 원자)에서도 실용적인 실행 시간을 확보했다.
하지만 탐욕적 알고리즘은 최적성을 보장하지 않는다. OCP의 최적 해를 구하는 것이 실제로 얼마나 어려운지에 대한 이론적 근거가 없었기 때문에, 연구자들은 “이 문제는 근본적으로 어려운가, 아니면 아직 적절한 알고리즘이 없을 뿐인가?”라는 의문을 품었다. 본 논문은 바로 이 질문에 답한다. 저자들은 강 NP‑완전 문제인 3‑Partition을 이용해 OCP로의 다항식 시간 감소를 설계하였다.
3‑Partition 문제는 주어진 3m개의 정수를 정확히 m개의 세 그룹으로 나누어 각 그룹의 합이 동일하도록 하는 문제이며, 이는 강하게 NP‑완전하다(입력 크기에 비례하는 수치가 제한된 경우에도 여전히 어려움). 논문에서는 각 정수를 OCP의 하이퍼엣지 비용에 매핑하고, 전체 예산을 “정확히 m개의 하이퍼엣지를 선택했을 때만 허용되는 최소 비용”으로 설정한다. 이렇게 하면 예산을 초과하면 비용이 급격히 증가해 최적 해가 될 수 없으며, 예산 이하이면서도 최소 비용을 달성하려면 반드시 3‑Partition의 유효한 분할과 일치하는 하이퍼엣지 집합을 선택해야 한다. 따라서 OCP의 최적 해를 구하는 것이 곧 3‑Partition을 푸는 것과 동등함을 증명한다.
이러한 증명은 두 가지 중요한 함의를 가진다. 첫째, OCP는 다항식 시간 알고리즘이 존재하지 않을 가능성이 높으며, 따라서 실제 단백질 구조 예측에서 최적 순서를 찾는 것은 이론적으로 불가능에 가깝다. 둘째, 현재 널리 사용되는 탐욕적 휴리스틱이 “근사 해”가 아닌 “실질적인 최선의 실용적 선택”임을 이론적으로 뒷받침한다. 즉, 휴리스틱이 제공하는 성능 향상이 우연이 아니라, 문제의 복잡도 한계 내에서 최선에 가까운 결과임을 정당화한다. 앞으로의 연구는 이러한 복잡도 장벽을 고려해, 근사 비율을 보장하는 알고리즘 설계나 특수한 인스턴스(예: 특정 단백질 군)에서의 파라미터 튜닝에 초점을 맞출 필요가 있다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리
