희소 단조 샤플리 회귀로 비선형 설명 가능성 구현

📝 원문 정보

• Title: Beyond Additivity: Sparse Isotonic Shapley Regression toward Nonlinear Explainability
• ArXiv ID: 2512.03112
• 발행일: 2025-12-02
• 저자: Jialai She

📝 초록 (Abstract)

샤플리 값은 설명 가능한 인공지능에서 가장 신뢰받는 특성 기여도 측정법이지만, 두 가지 근본적인 한계가 있다. 첫째, 전통적인 샤플리 프레임워크는 가치 함수가 가법적이라고 가정하지만, 실제 데이터는 비정규분포, 중대한 꼬리, 변수 간 의존성, 혹은 도메인 특화 손실 척도 등에 의해 이 가정을 위배한다. 이로 인해 기여도가 왜곡된다. 둘째, 고차원 상황에서 희소한 설명을 얻기 위해 밀집된 샤플리 값을 계산한 뒤 임의로 임계값을 적용하는 방법은 계산 비용이 크게 늘고 일관성을 보장하지 못한다. 본 논문은 이러한 문제를 해결하기 위해 Sparse Isotonic Shapley Regression(SISR)을 제안한다. SISR은 가법성을 회복하기 위한 단조 변환을 동시에 학습하고, 샤플리 벡터에 L0 희소성 제약을 부여하여 대규모 특성 공간에서도 효율적인 계산을 가능하게 한다. 최적화 과정은 Pool‑Adjacent‑Violators 알고리즘을 이용한 단조 회귀와 정규화된 하드 임계값을 통한 지원 집합 선택을 결합해 구현이 간단하면서 전역 수렴을 보장한다. 이론적 분석을 통해 SISR이 다양한 상황에서 진정한 변환을 복원하고, 높은 잡음 하에서도 강력한 지원 복구 능력을 갖춤을 증명한다. 또한, 관련 없는 특성 및 특성 간 의존성이 실제 가치 변환을 크게 비선형적으로 만들 수 있음을 최초로 보인다. 회귀, 로지스틱 회귀, 트리 앙상블 등 다양한 실험에서 SISR은 지급 방식에 관계없이 기여도를 안정화하고, 불필요한 특성을 정확히 걸러내는 반면, 기존 샤플리 값은 순위와 부호가 크게 왜곡되는 것을 확인하였다. 비선형 설명 가능성 분야에 이론적·실용적 기여를 제공한다.

💡 논문 핵심 해설 (Deep Analysis)

샤플리 값은 협력 게임 이론에 기반한 특성 기여도 측정법으로, 각 특성이 모델 출력에 미치는 평균적인 기여를 공정하게 분배한다는 점에서 ‘골드 스탠다드’로 평가받아 왔다. 그러나 이 프레임워크는 두 가지 핵심 전제가 실제 머신러닝 실무에서 자주 깨진다. 첫 번째 전제는 가치 함수, 즉 모델이 예측한 결과와 실제 관측값 사이의 손실(또는 보상)이 특성들의 가법적 조합으로 표현될 수 있다는 가정이다. 현실에서는 입력 변수들이 복잡하게 얽혀 비선형 상호작용을 형성하고, 데이터 분포 자체가 비정규, 중대한 꼬리, 혹은 다중공선성을 띠는 경우가 빈번하다. 이러한 상황에서는 손실 함수가 단순히 각 특성의 독립적인 기여 합으로 분해되지 않으며, 샤플리 값을 그대로 적용하면 특성의 실제 영향력이 과소·과대 평가되는 왜곡이 발생한다. 두 번째 전제는 샤플리 값을 계산한 뒤, 필요에 따라 임계값을 적용해 희소한 설명을 얻는 것이 가능하다는 점이다. 하지만 샤플리 값 자체는 모든 특성에 대해 비제로 값을 갖는 ‘밀집’ 벡터이며, 고차원 데이터(수천~수만 차원)에서는 정확히 계산하는 데 조합 폭이 기하급수적으로 늘어나 실용적이지 않다. 게다가 사후 임계값 적용은 임의적이며, 동일한 데이터에 대해 다른 임계값을 선택하면 전혀 다른 설명이 도출될 위험이 있다.

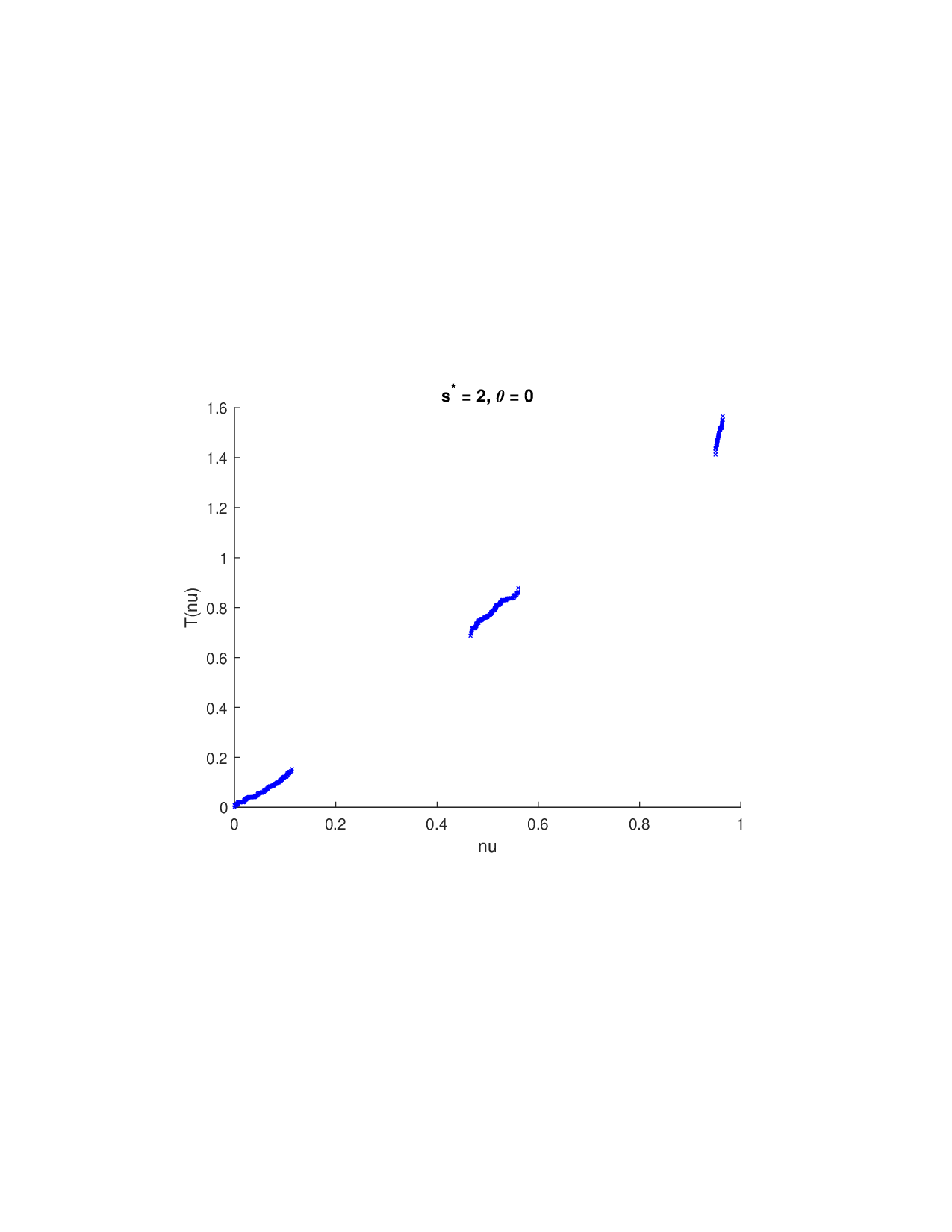
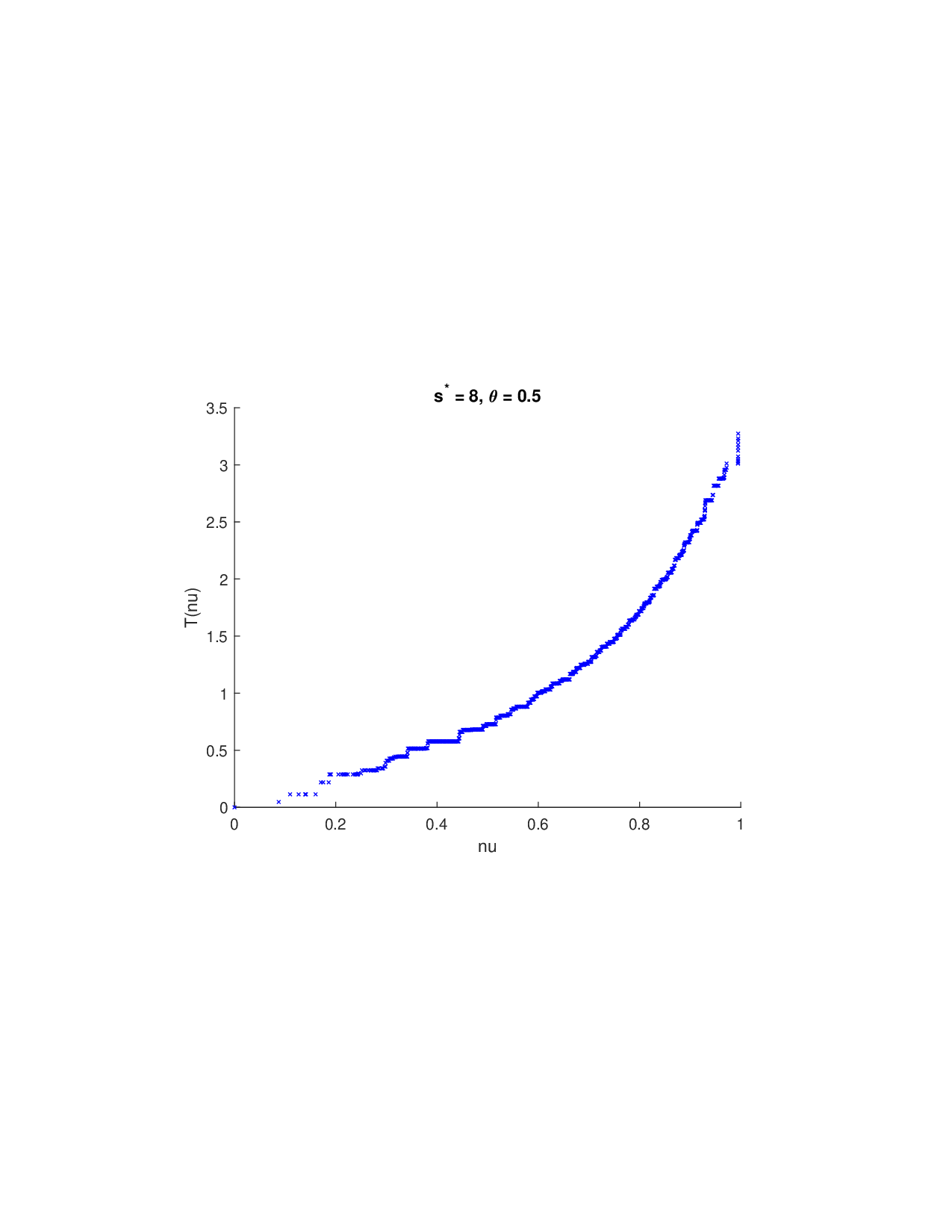
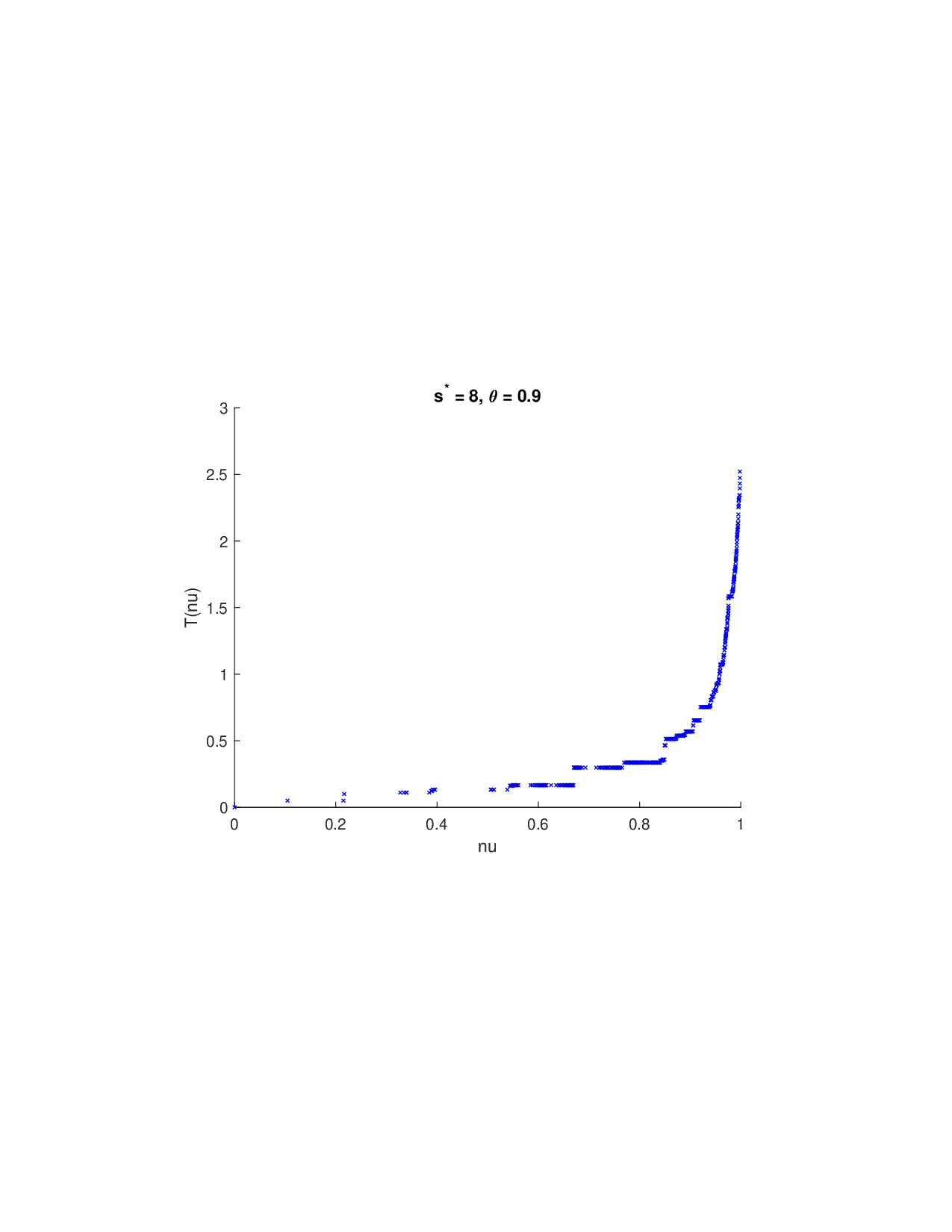
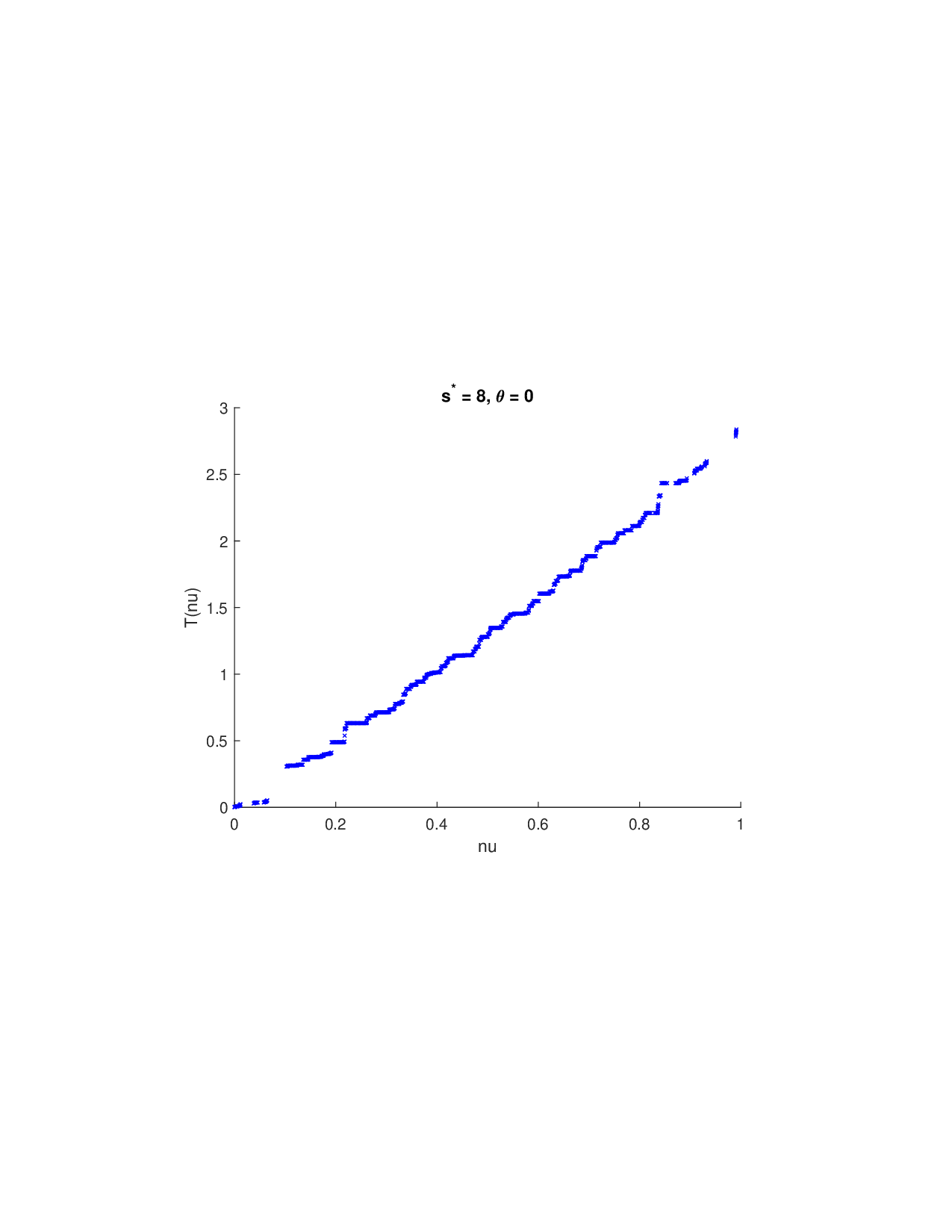
SISR은 이러한 문제를 근본적으로 해결한다. 핵심 아이디어는 ‘단조 변환(isotonic transformation)’을 도입해 원래의 비가법적 가치 함수를 가법적으로 만들면서, 동시에 샤플리 벡터에 L0 제약을 부여해 희소성을 보장하는 것이다. 단조 변환은 입력값의 순서를 보존하면서 함수 형태를 자유롭게 조정한다. 즉, 특성들의 기여도가 증가하면 변환된 가치도 반드시 증가한다는 단조성만을 요구하므로, 복잡한 비선형 구조를 손쉽게 포착한다. 이때 Pool‑Adjacent‑Violators Algorithm(PAVA)을 사용하면 O(n) 시간에 전역 최적의 단조 회귀 해를 얻을 수 있어 계산 효율성이 뛰어나다.

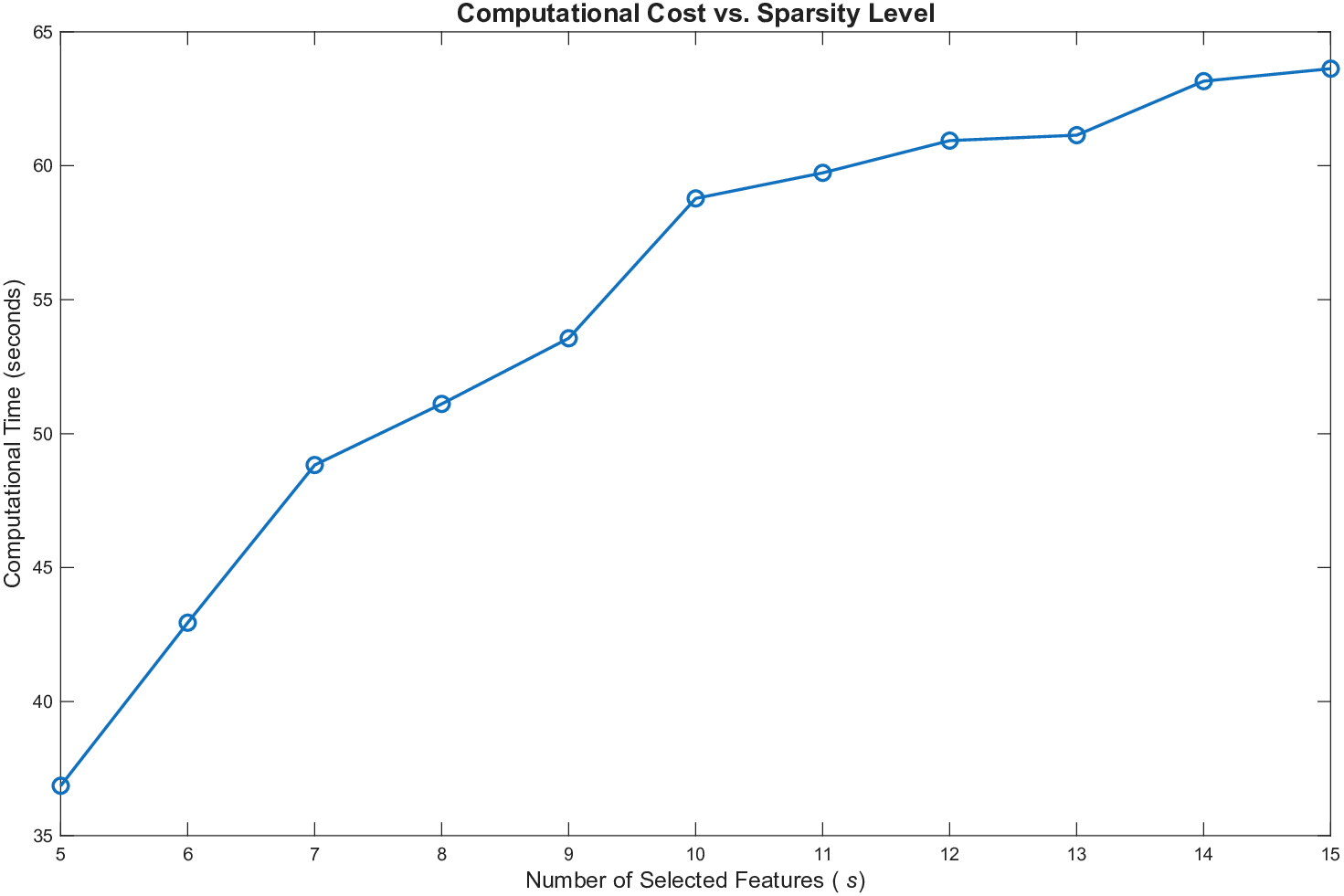
희소성 제어는 L0 규제로 구현된다. 기존 연구들은 L1 혹은 연속적인 근사 방법을 쓰지만, 이는 실제 ‘제로’ 특성을 완전히 배제하지 못한다. SISR은 정규화된 하드 임계값(normalized hard‑thresholding) 연산을 통해 가장 큰 절대값을 가진 k개의 특성만을 선택하고 나머지는 정확히 0으로 만든다. 이 과정은 매 반복마다 지원 집합을 재평가하므로, 불필요한 특성이 다시 활성화되는 현상을 방지한다. 알고리즘은 단조 회귀와 하드 임계값을 교대로 수행하는 블록 좌표 상승(block coordinate ascent) 형태이며, 각 단계에서 전역 최적을 보장하므로 전체 알고리즘도 전역 수렴성을 갖는다.

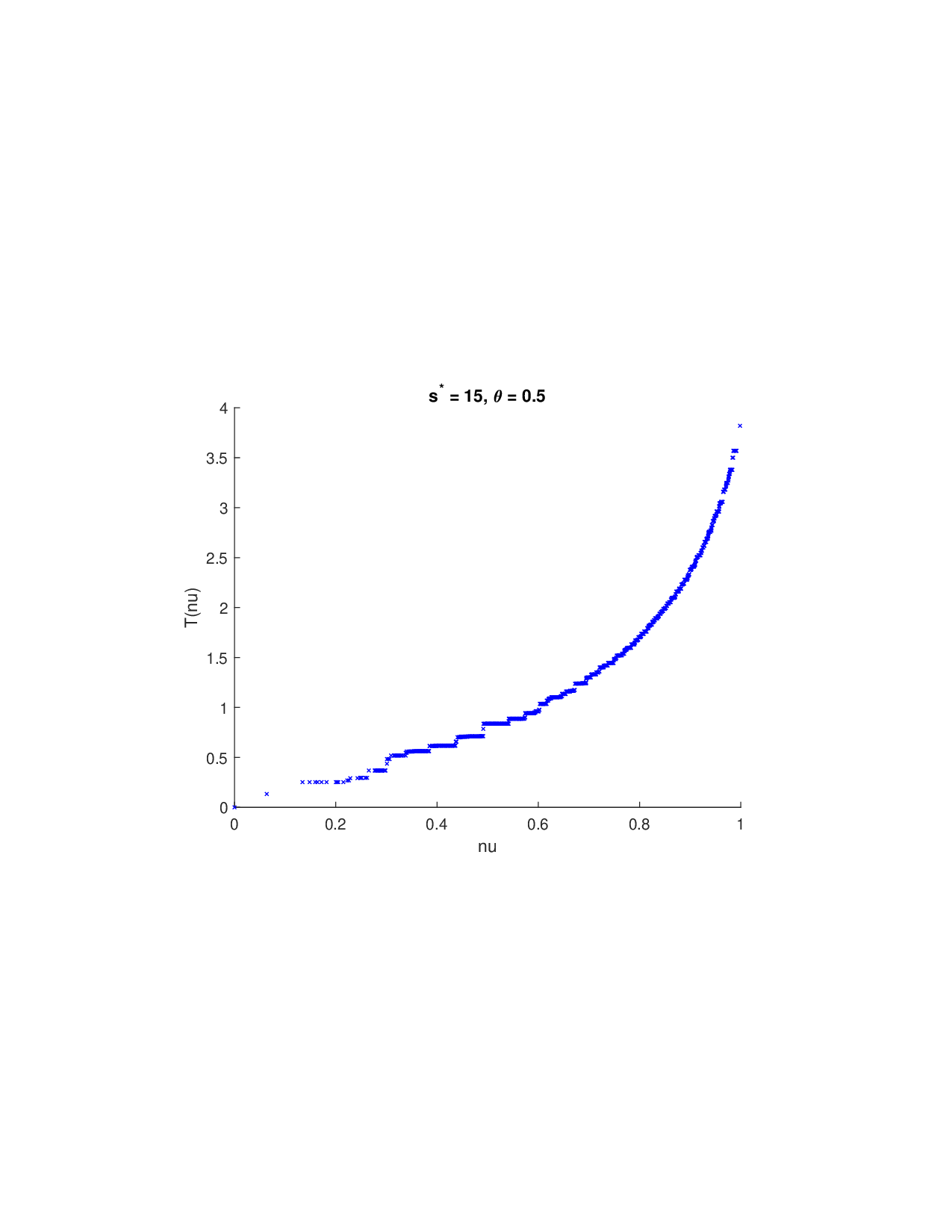
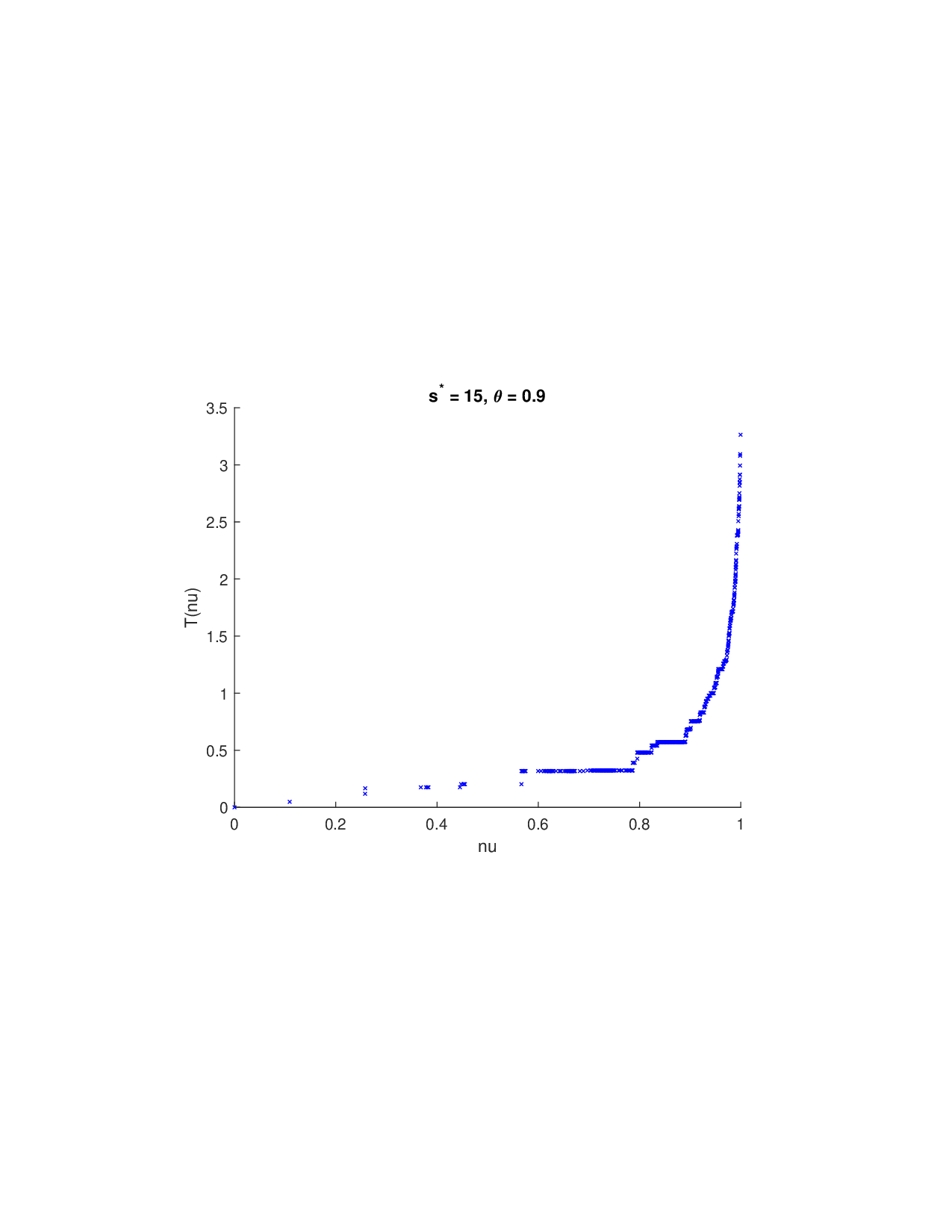
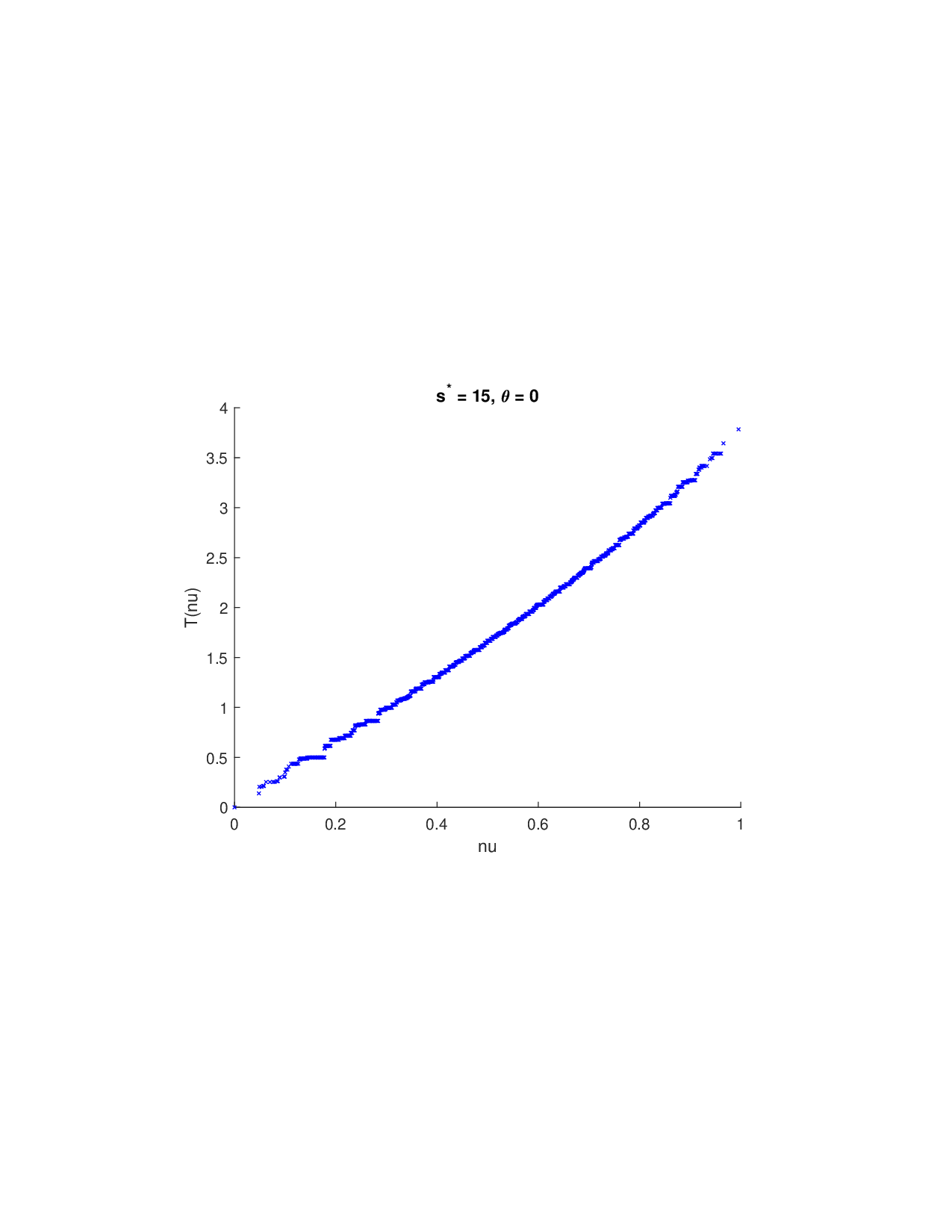
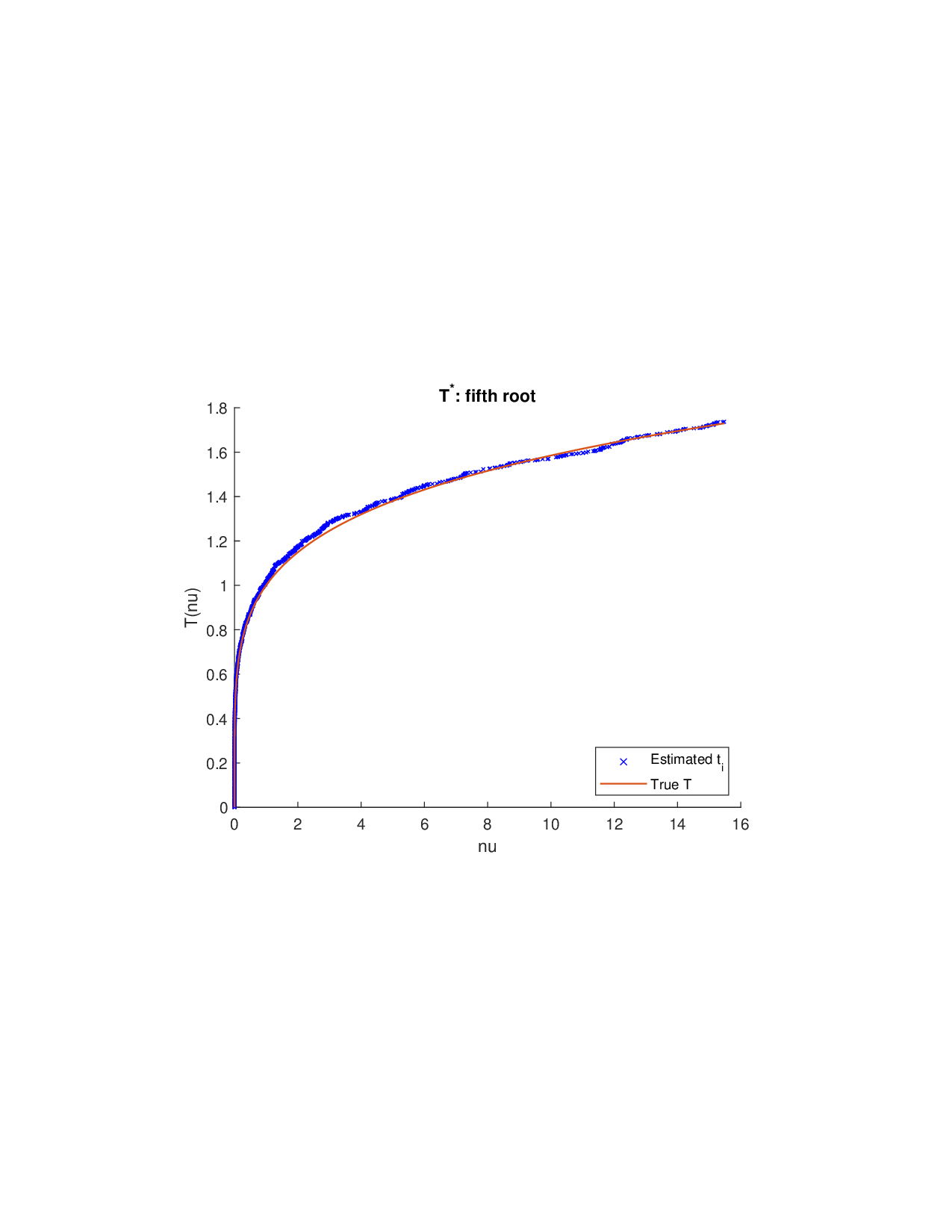
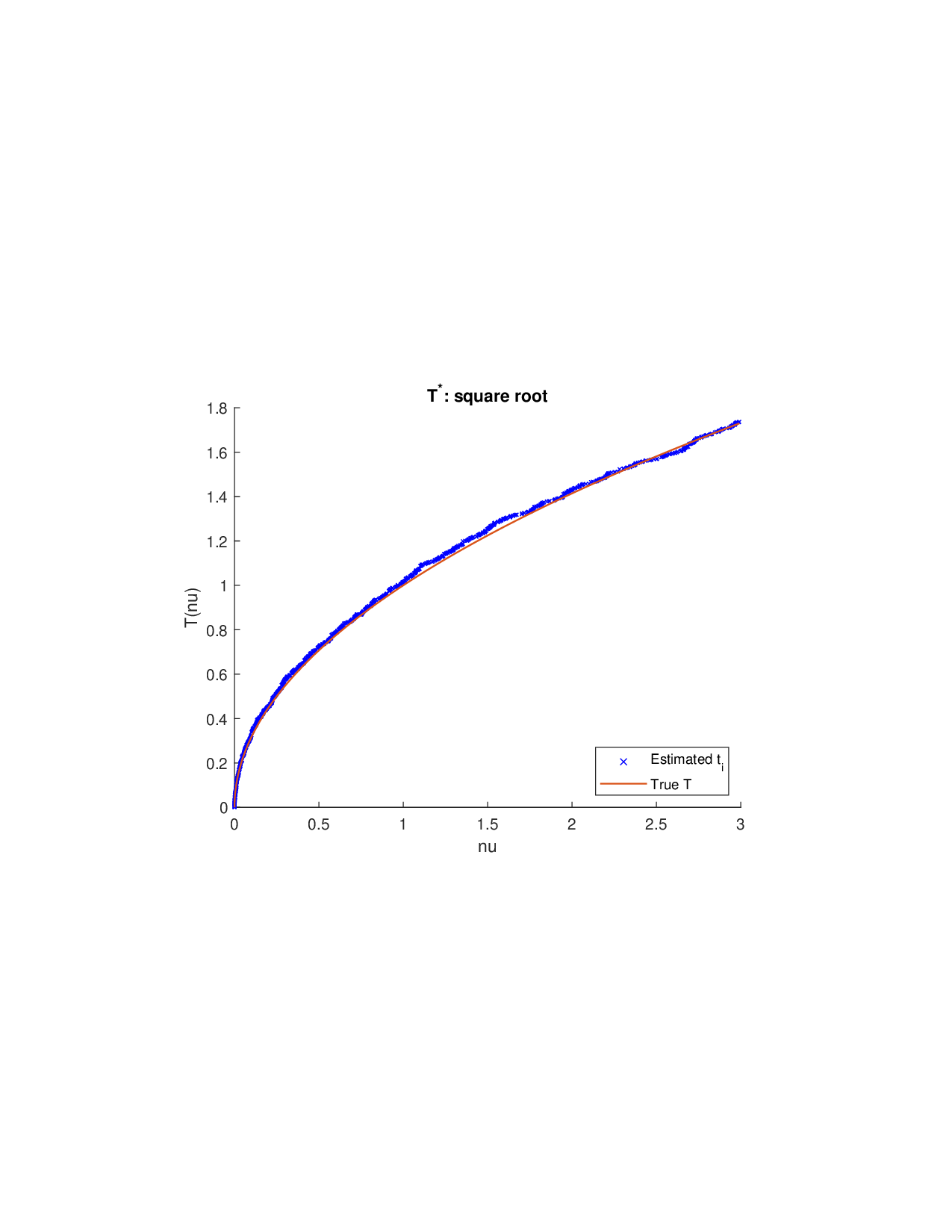
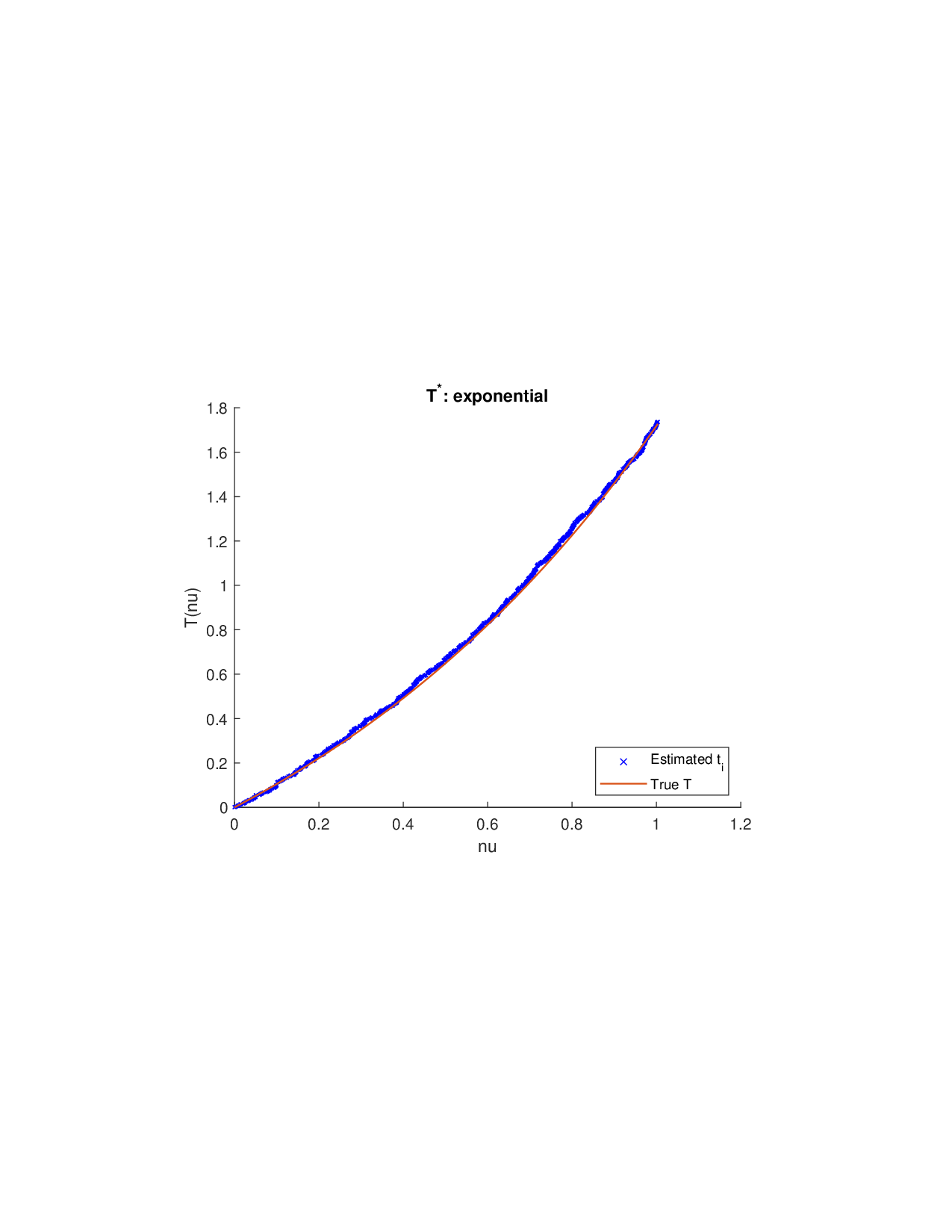
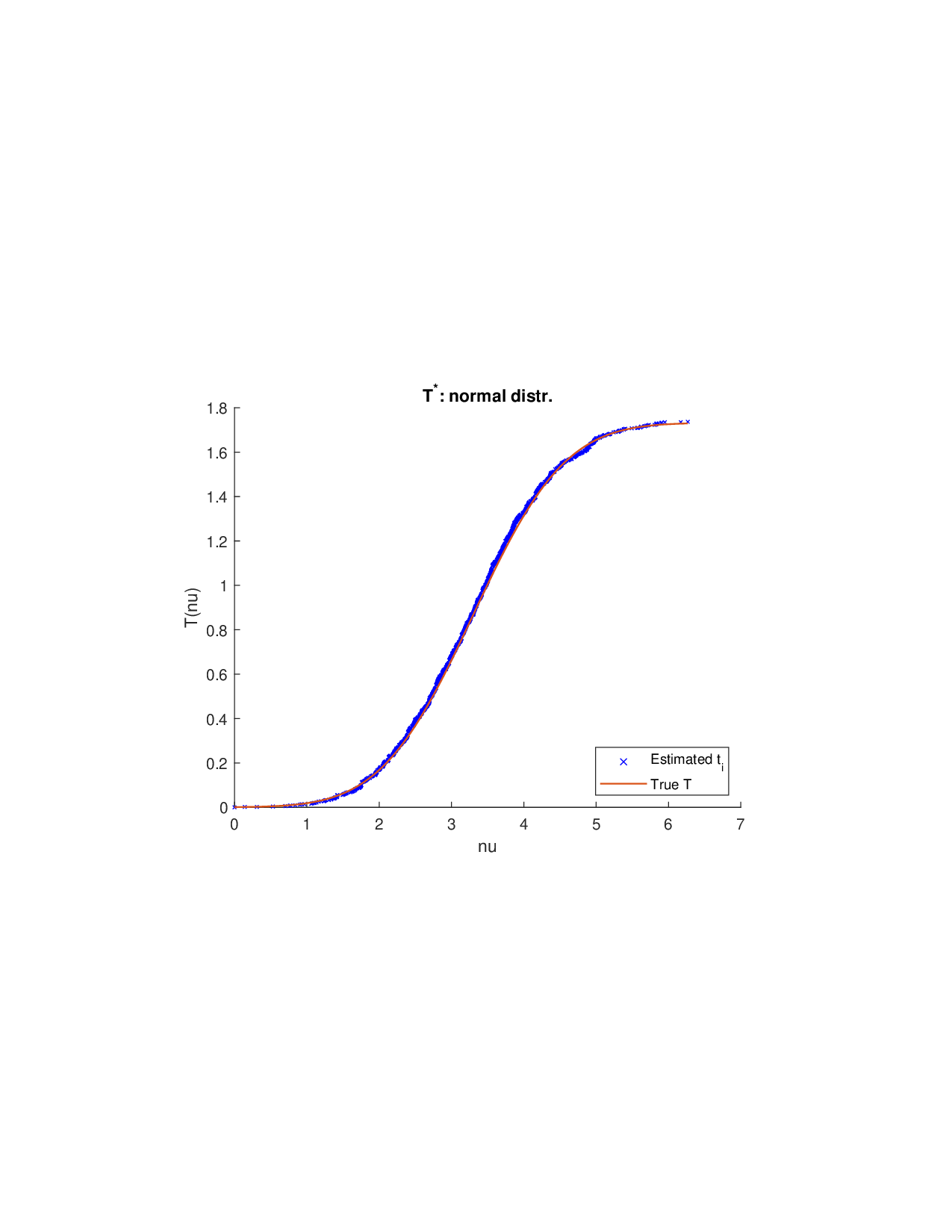
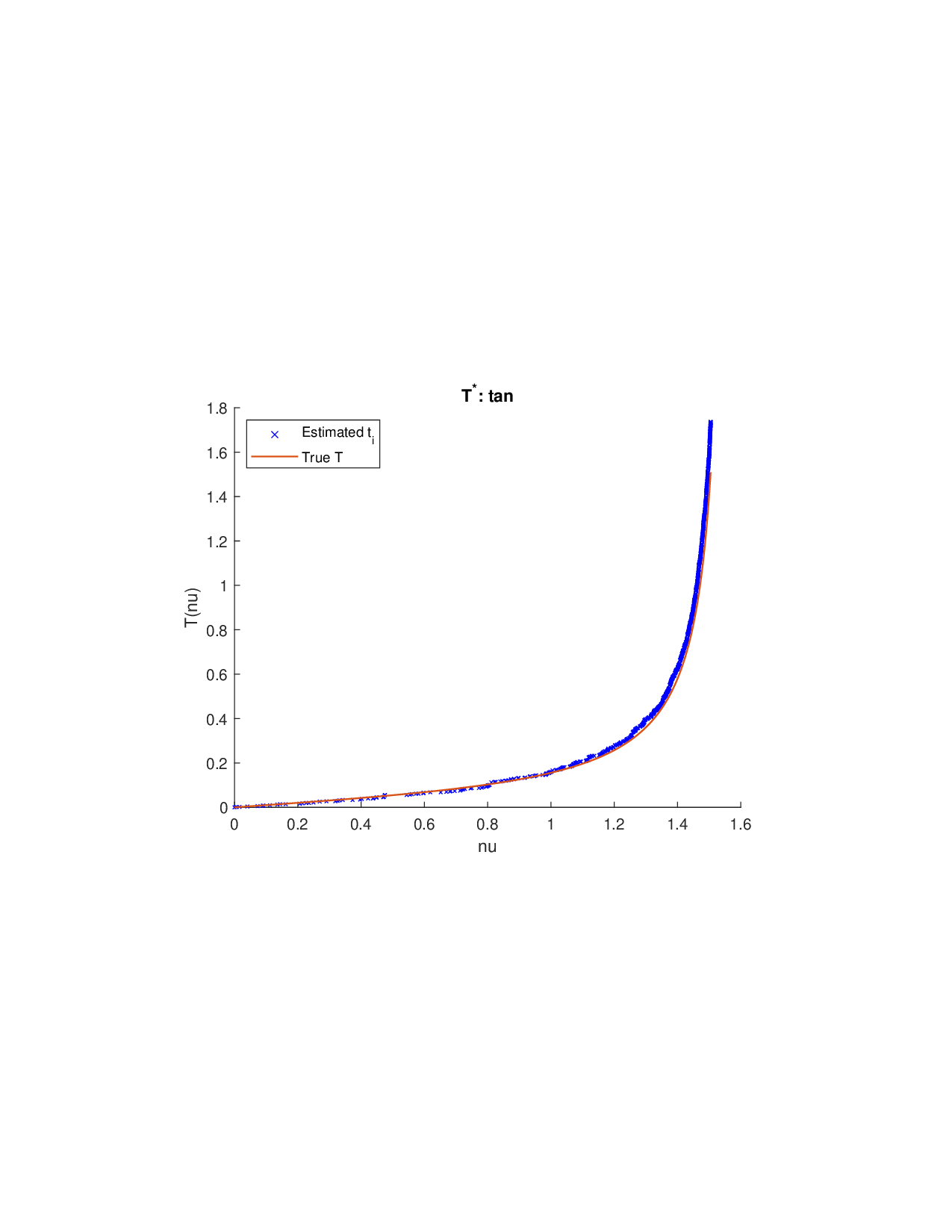
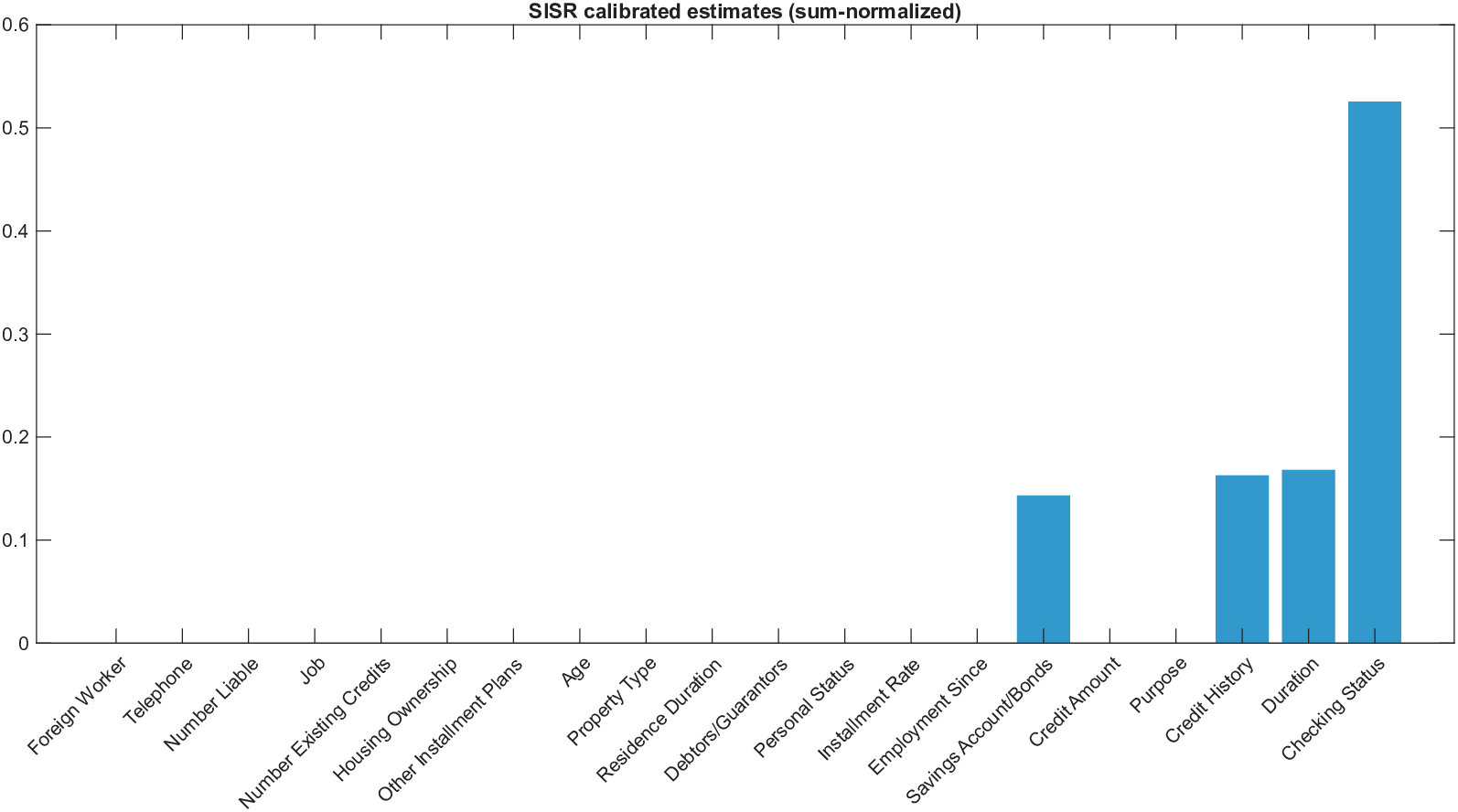
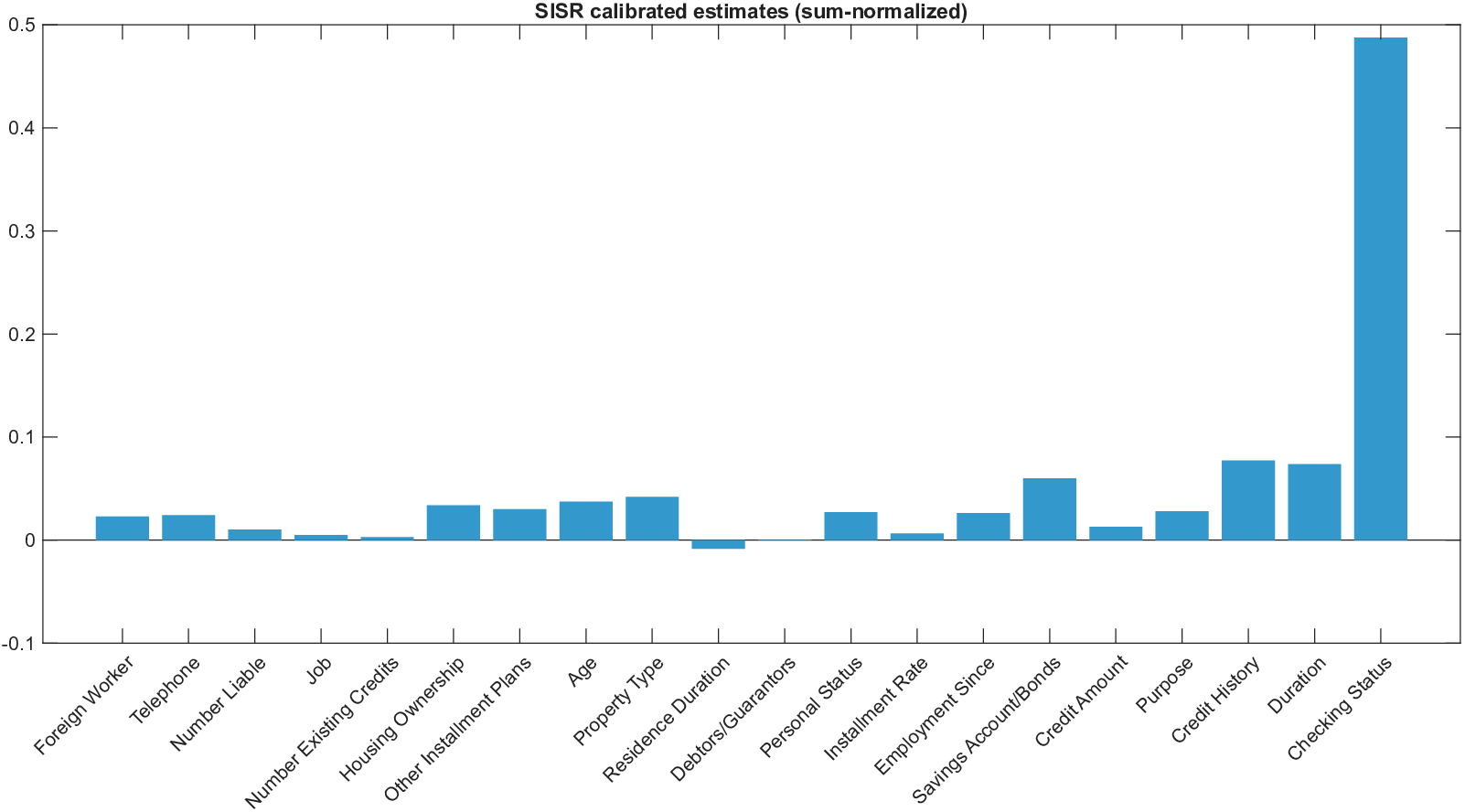
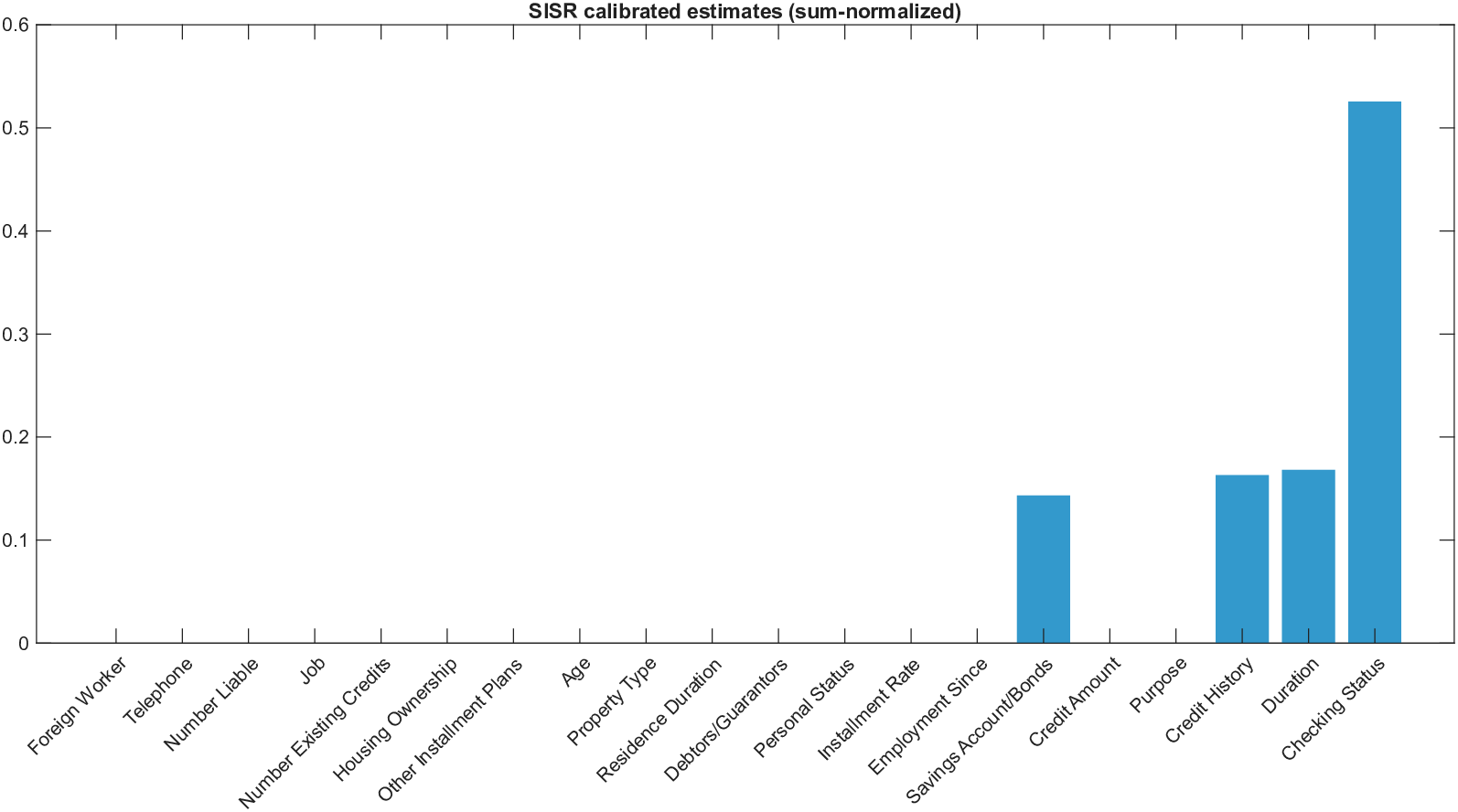
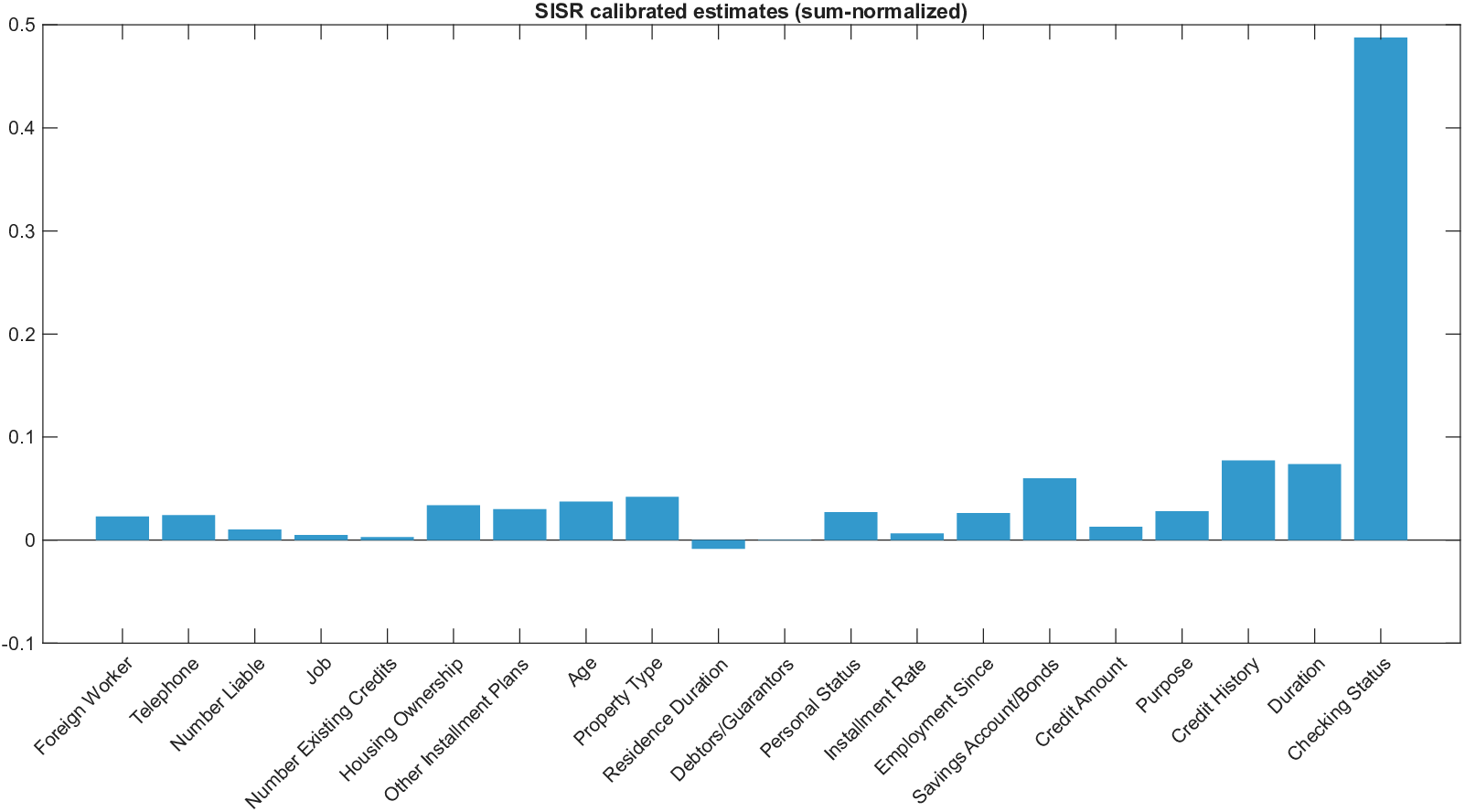
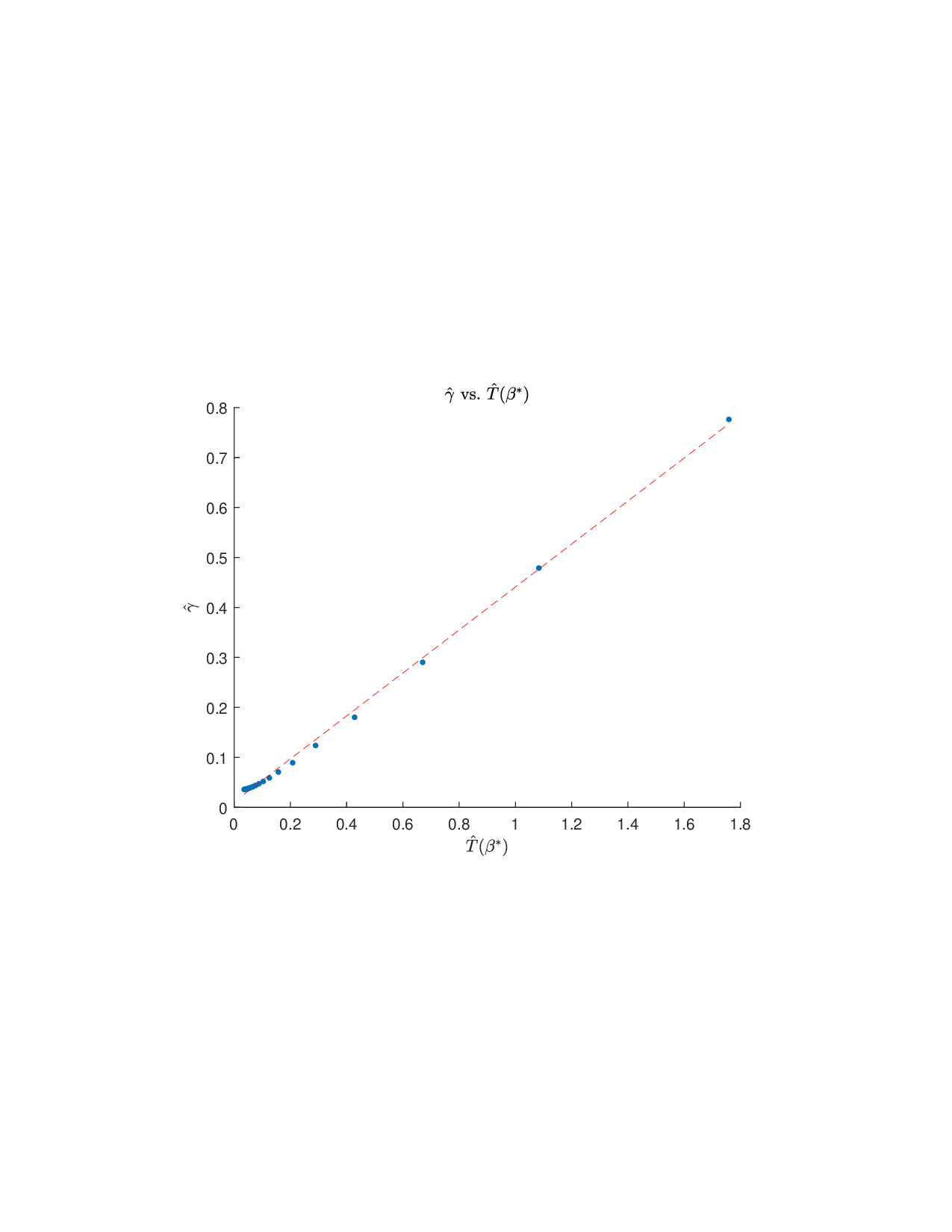
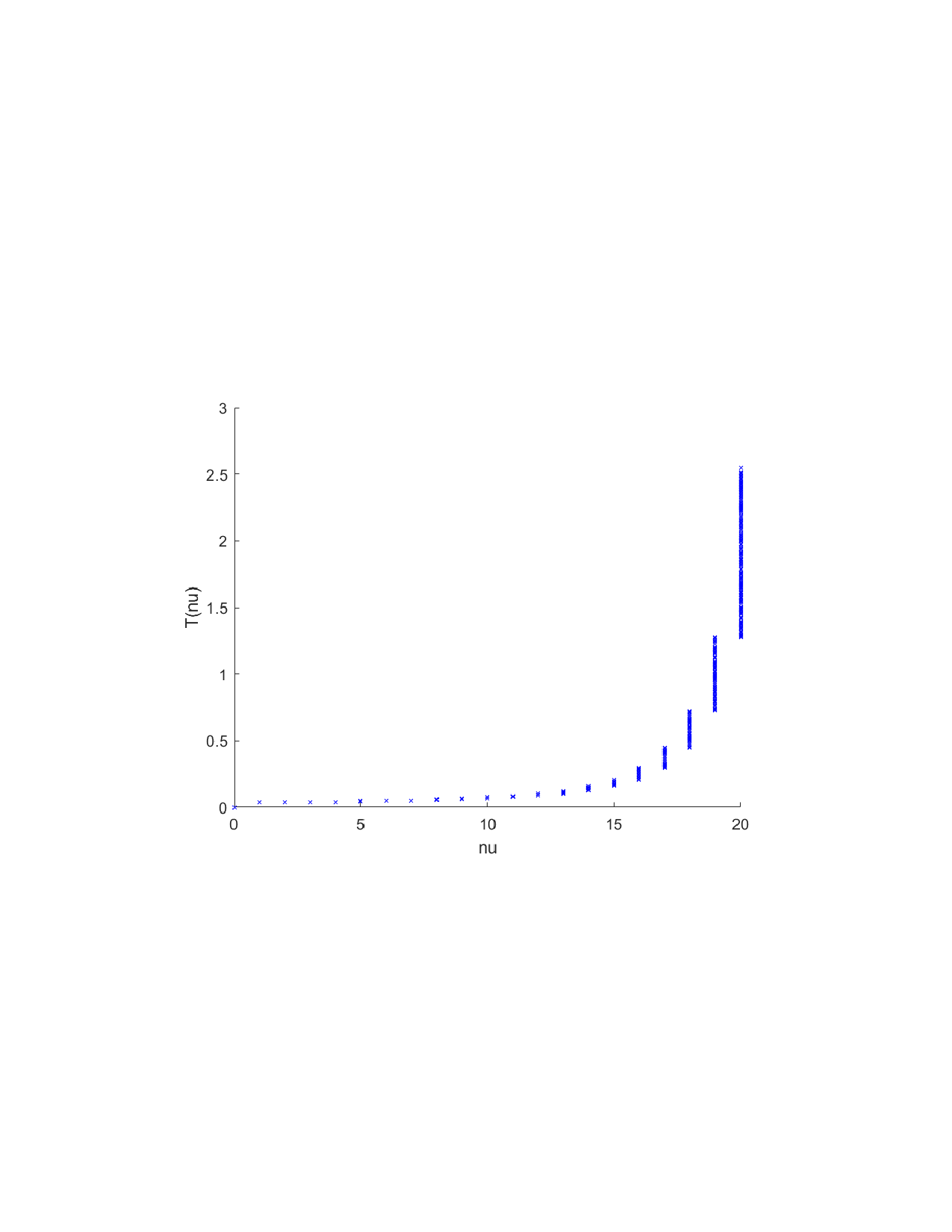
이론적 분석에서는 두 가지 주요 결과를 제시한다. 첫째, 충분히 풍부한 샘플과 적당한 정규화가 주어지면 SISR은 실제 단조 변환 함수를 일관적으로 복원한다는 일관성(consistency) 정리를 증명한다. 둘째, 잡음이 존재하는 고차원 상황에서도 최소 신호 강도 조건(minimum signal strength) 하에 L0 제약이 정확한 지원 집합을 복구한다는 지원 복구(support recovery) 보장을 제공한다. 특히, 논문은 ‘irrelevant features’와 ‘inter‑feature dependencies’가 존재할 때, 실제 가치 함수가 강한 비선형 왜곡을 겪으며, 이때 단조 변환이 없으면 샤플리 값이 순위와 부호까지 뒤바뀌는 현상이 발생한다는 실증적 증거를 제시한다.

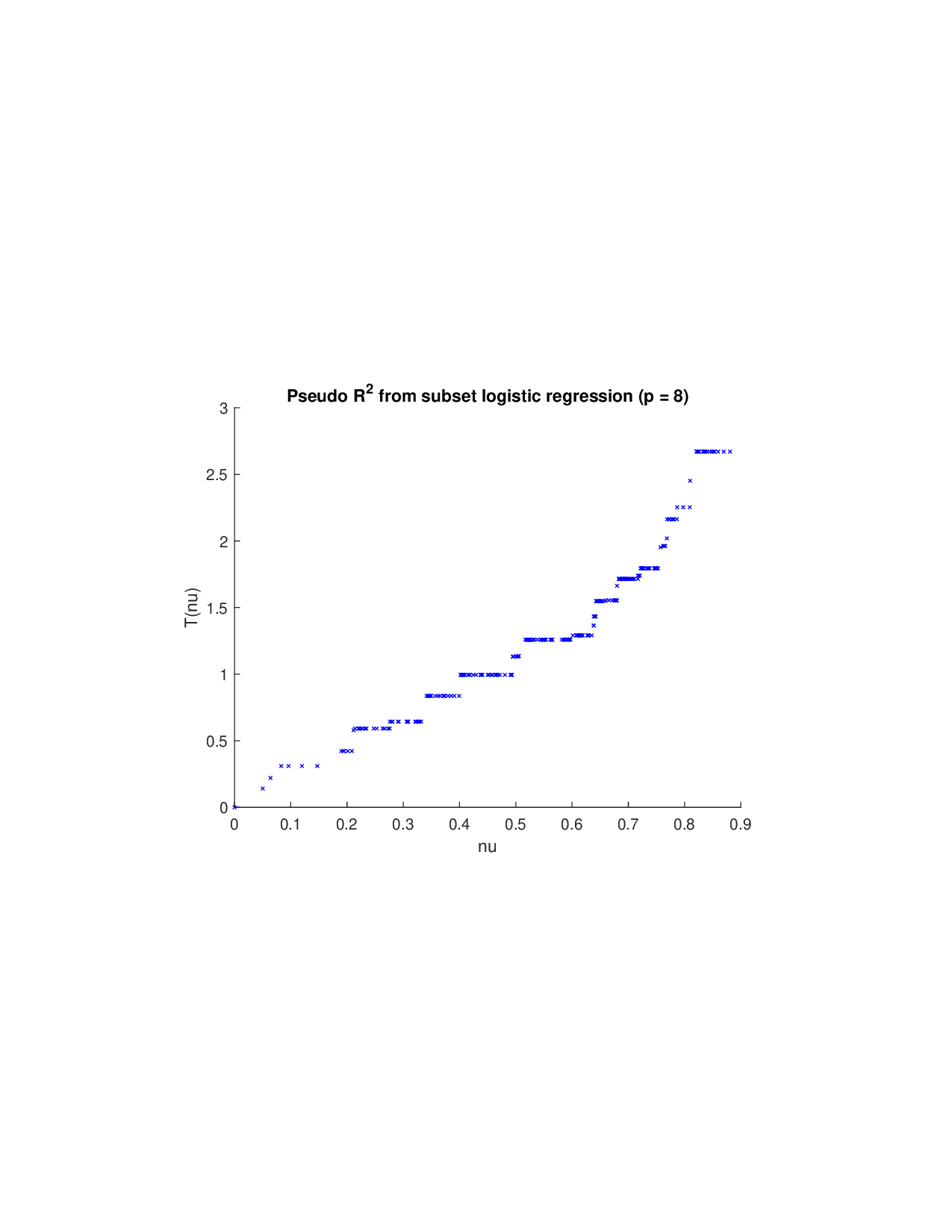
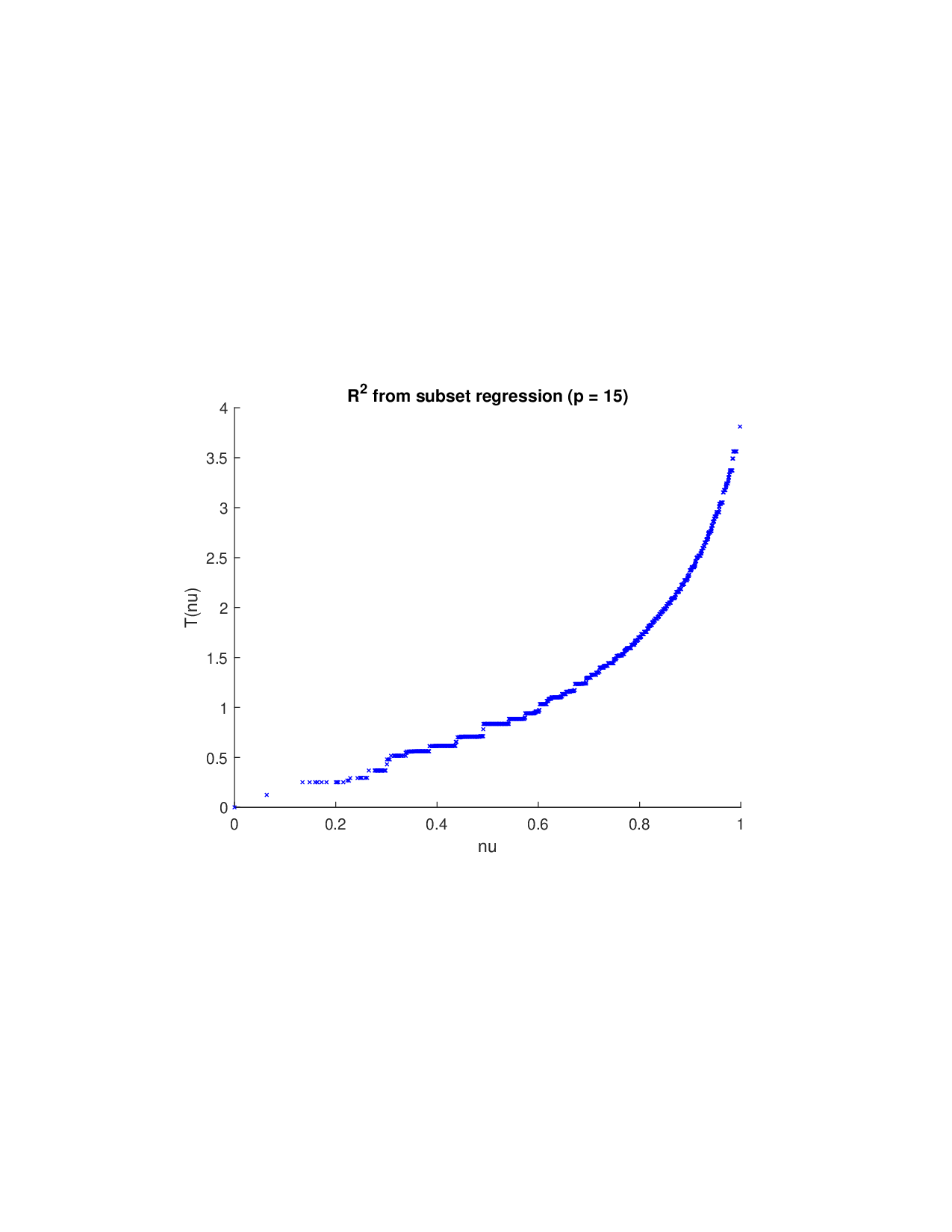
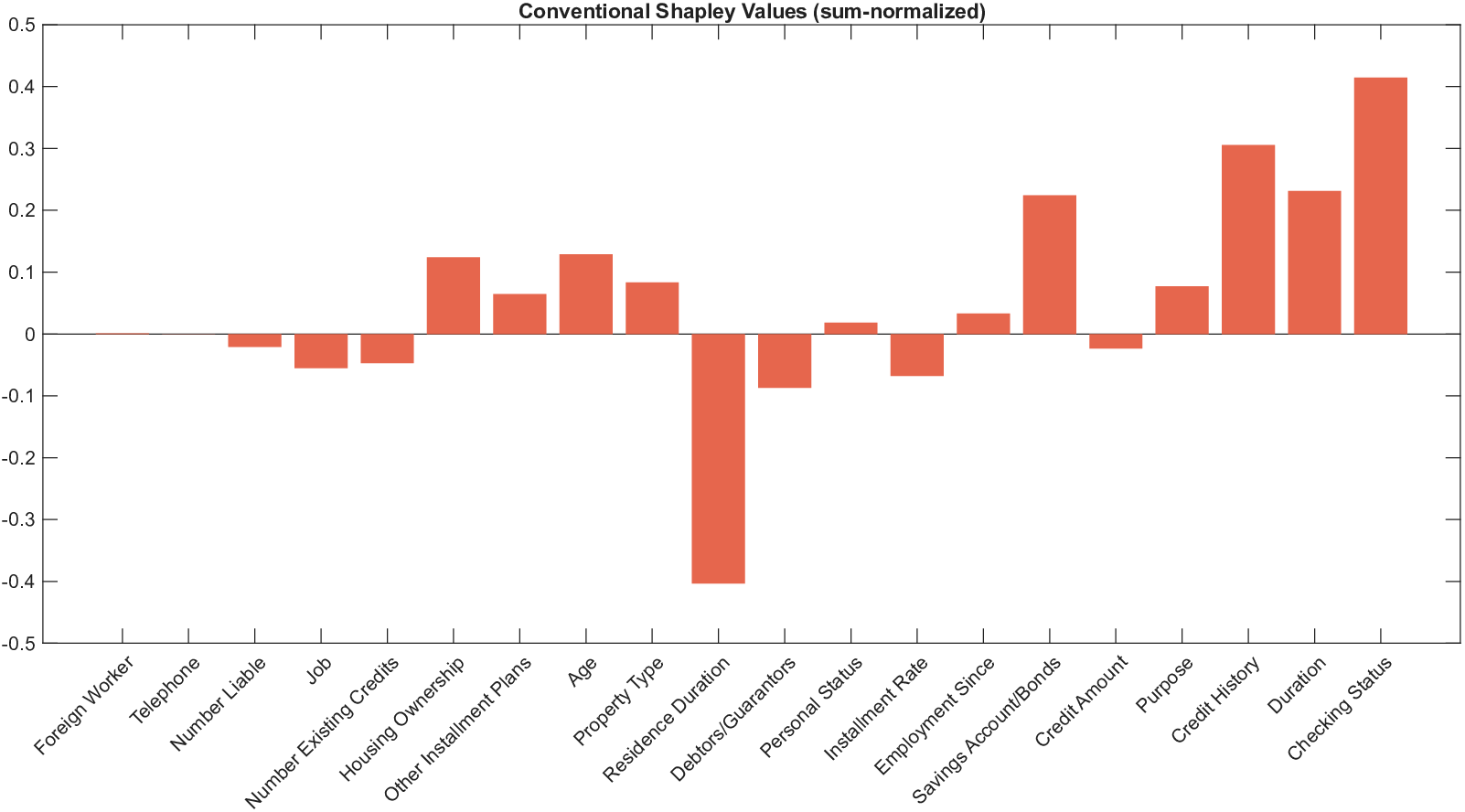
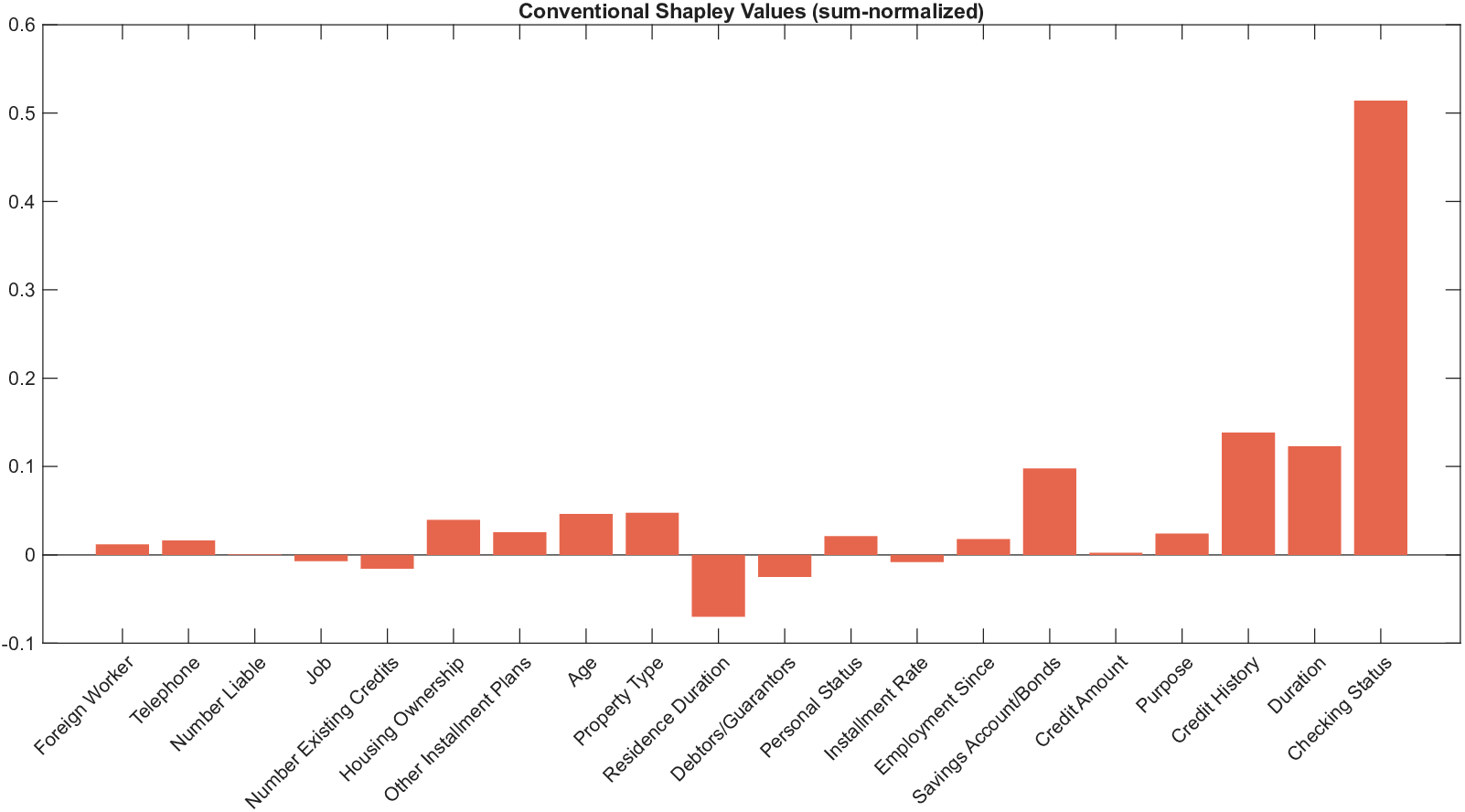
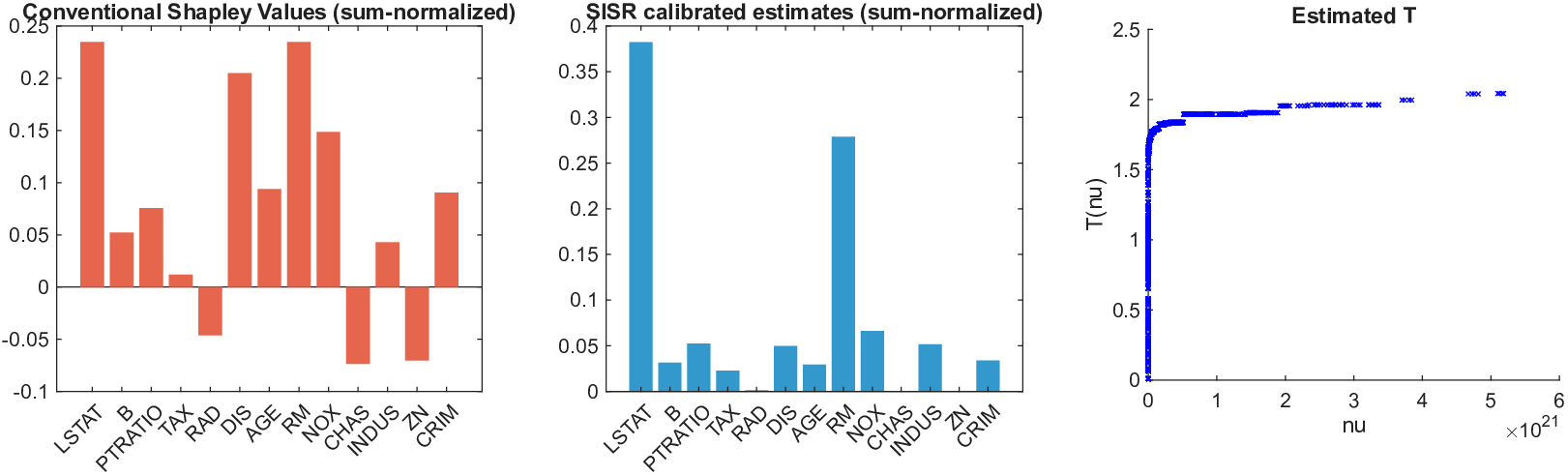
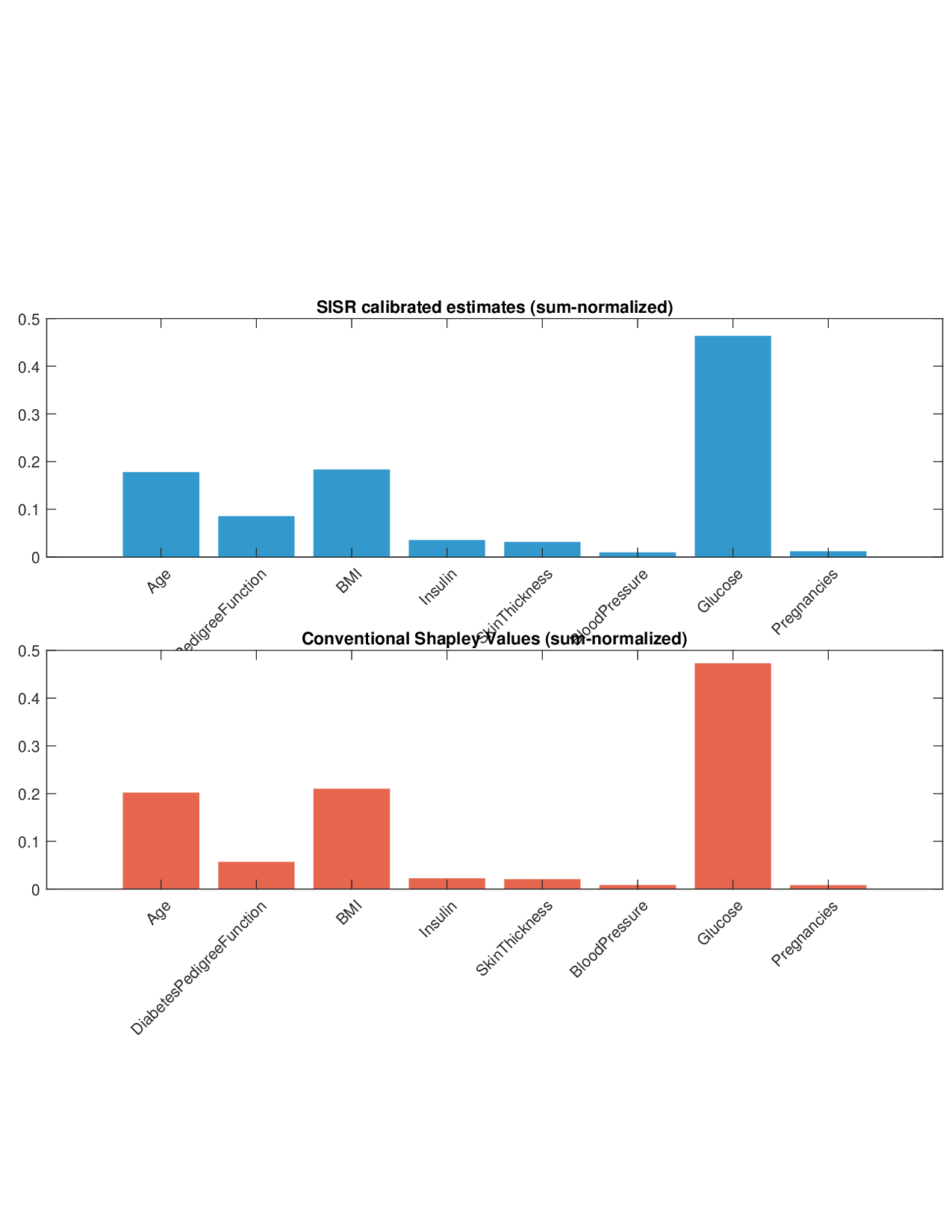
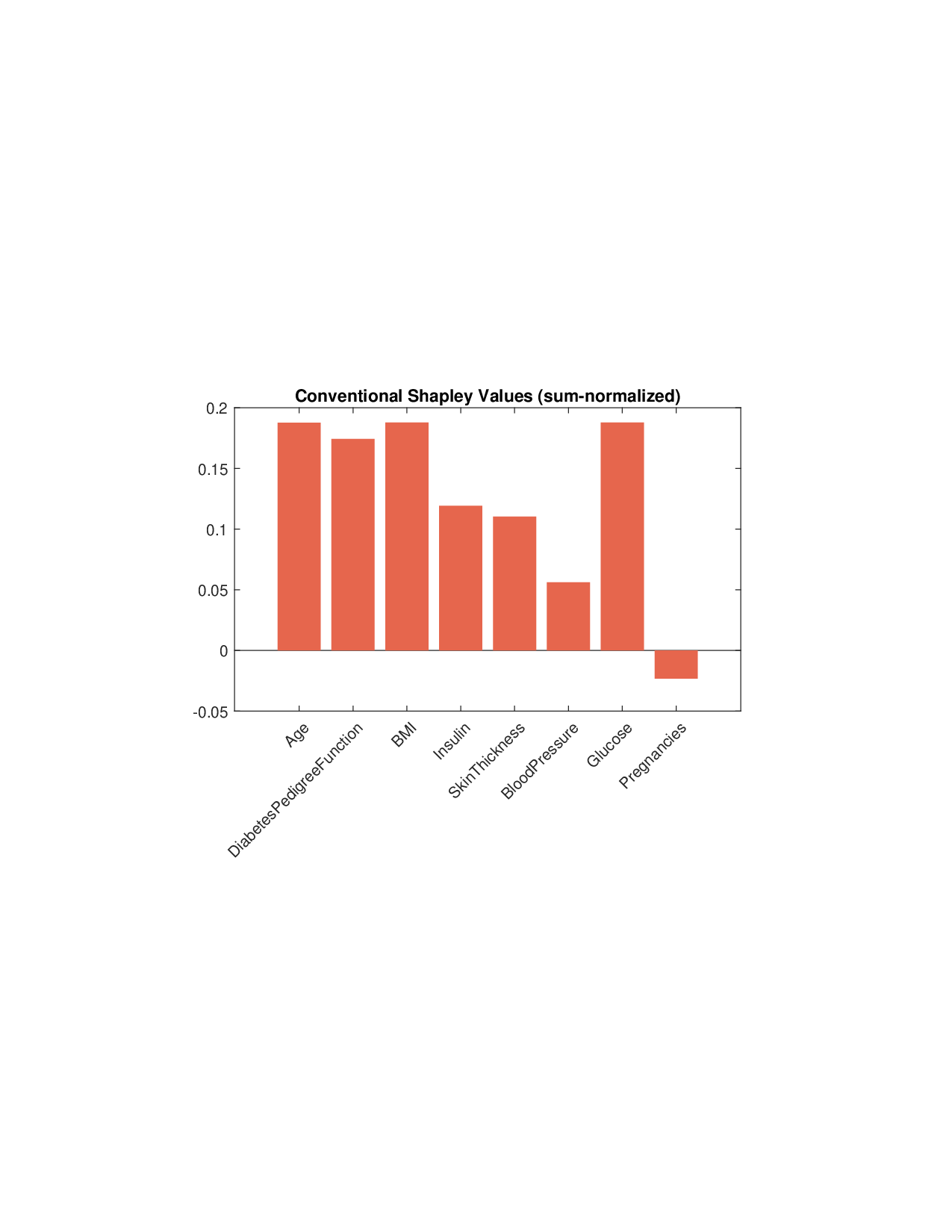
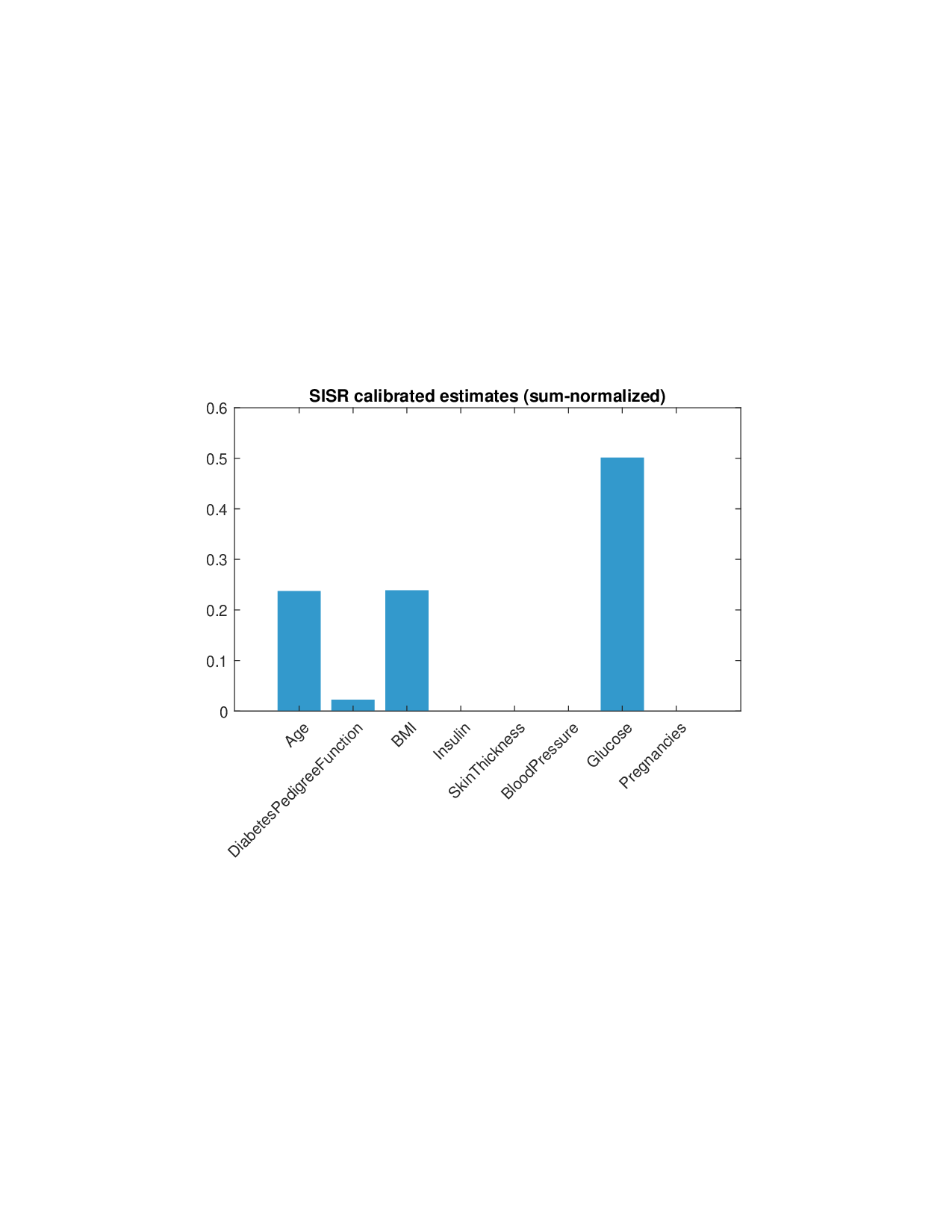
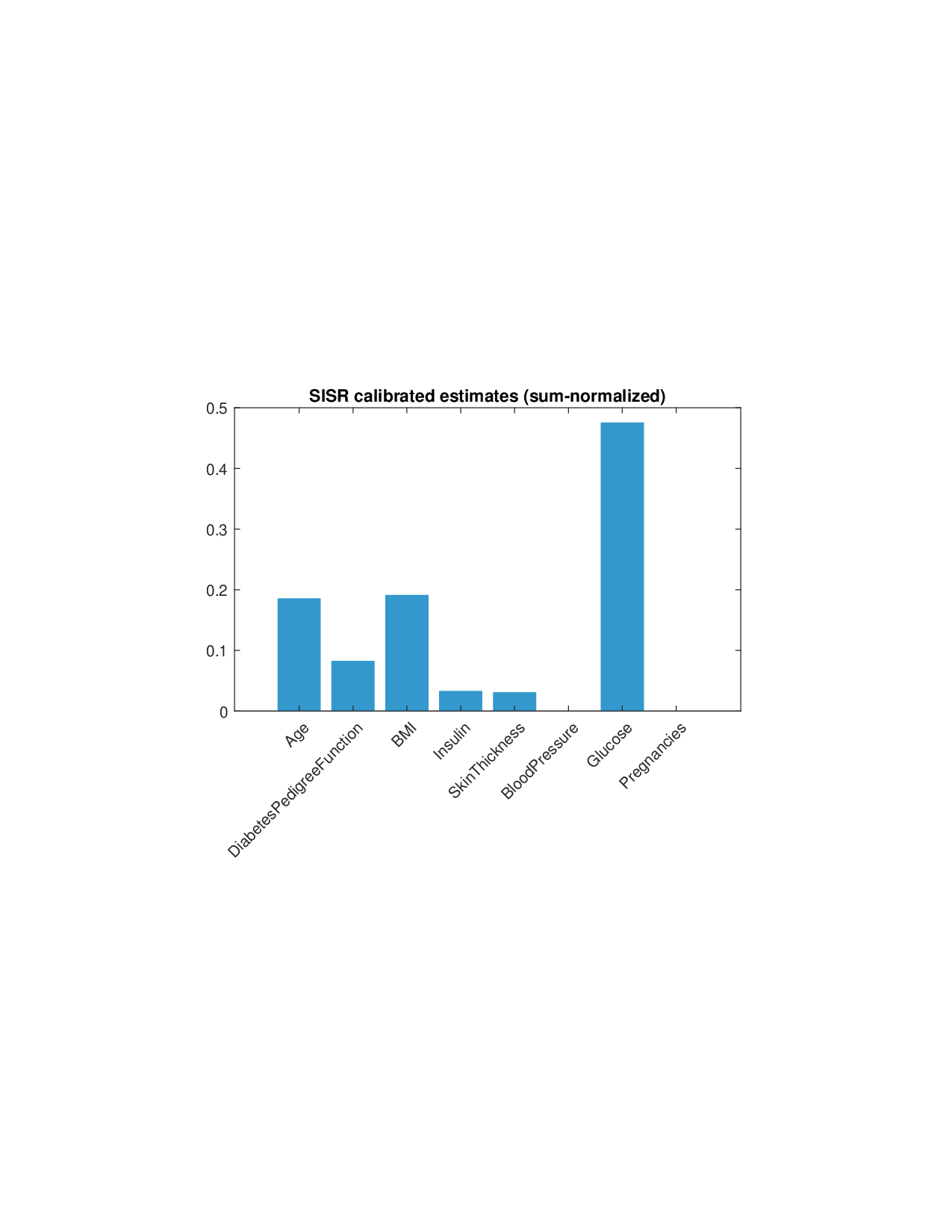
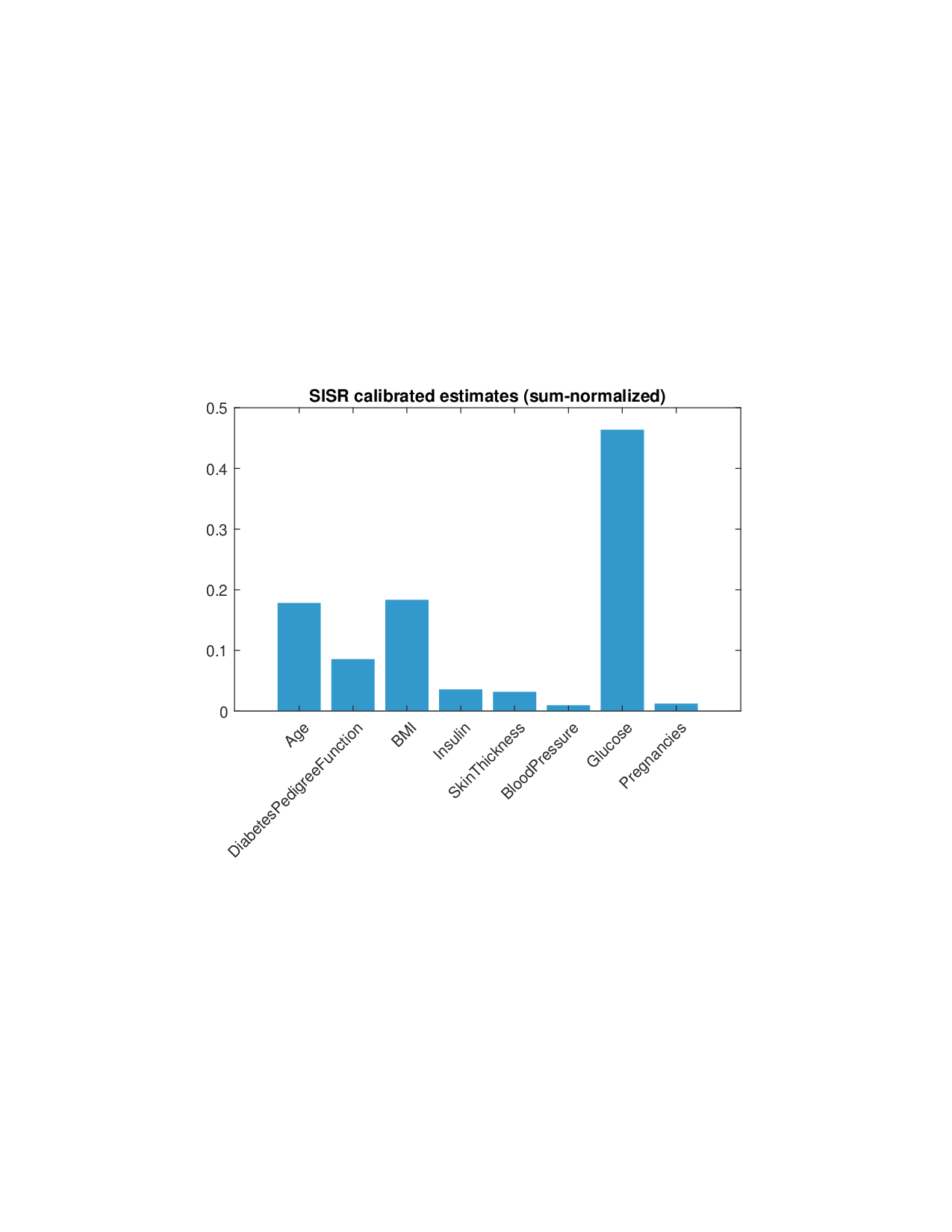
실험 부분에서는 회귀, 로지스틱 회귀, 그리고 XGBoost·LightGBM과 같은 트리 기반 앙상블 모델을 대상으로 다양한 지급 스킴(예: MSE, MAE, 로그우도, 비용 기반 손실)을 적용하였다. 결과는 SISR이 변환 전후의 샤플리 값 차이를 최소화하고, 불필요한 특성을 0으로 정확히 억제함으로써 설명의 안정성과 해석성을 크게 향상시켰음을 보여준다. 반면 기존 샤플리 방법은 동일한 데이터셋에서도 특성 순위가 크게 뒤바뀌고, 부호가 반전되는 등 신뢰성을 크게 잃었다.

요약하면, SISR은 (1) 비가법적 가치 함수를 단조 변환으로 가법화, (2) L0 희소성을 통해 고차원에서도 실용적인 설명 제공, (3) 효율적인 PAVA 기반 최적화와 전역 수렴 보장이라는 세 축을 결합한 혁신적 프레임워크이다. 이는 Explainable AI 분야에서 비선형·고차원 모델에 대한 이론적 근거와 실용적 도구를 동시에 제공한다는 점에서 큰 의미를 가진다.

📄 논문 본문 발췌 (Translation)

📸 추가 이미지 갤러리

Reference