선택적 예측의 거짓 발견률 제어를 위한 LEC 프레임워크
📝 원문 정보
- Title: A Linear Expectation Constraint for Selective Prediction and Routing with False-Discovery Control
- ArXiv ID: 2512.01556
- 발행일: 2025-12-01
- 저자: Zhiyuan Wang, Aniri, Tianlong Chen, Yue Zhang, Heng Tao Shen, Xiaoshuang Shi, Kaidi Xu
📝 초록 (Abstract)
기초 모델은 종종 신뢰할 수 없는 답변을 생성하지만, 기존의 휴리스틱 불확실성 추정기는 정답과 오답을 완전히 구분하지 못해 사용자가 오류를 통계적 보증 없이 받아들이게 된다. 본 연구는 허위 발견률(FDR) 제어 관점에서 이 문제를 접근한다. 즉, 채택된 모든 예측 중 오류 비율이 사전에 설정한 위험 수준을 초과하지 않도록 보장한다. 이를 위해 선택적 예측을 선택 지표와 오류 지표에 대한 선형 기대 제약으로 정의하는 LEC라는 원칙적인 프레임워크를 제안한다. 이 형식화 아래, 교환 가능한 보정 데이터의 보유 집합만을 이용해 충분조건을 도출하고, FDR 제약 하에 보유율을 최대화하는 임계값을 계산한다. 또한, 기본 모델의 불확실성이 임계값을 초과할 경우 입력을 후속 모델에 위임하는 두 모델 라우팅 시스템으로 확장하여 시스템 전체의 FDR을 유지한다. 폐쇄형·개방형 질문응답(QA) 및 시각 질문응답(VQA) 실험에서 LEC는 기존 방법에 비해 더 엄격한 FDR 제어와 현저한 샘플 보유율 향상을 달성한다.💡 논문 핵심 해설 (Deep Analysis)
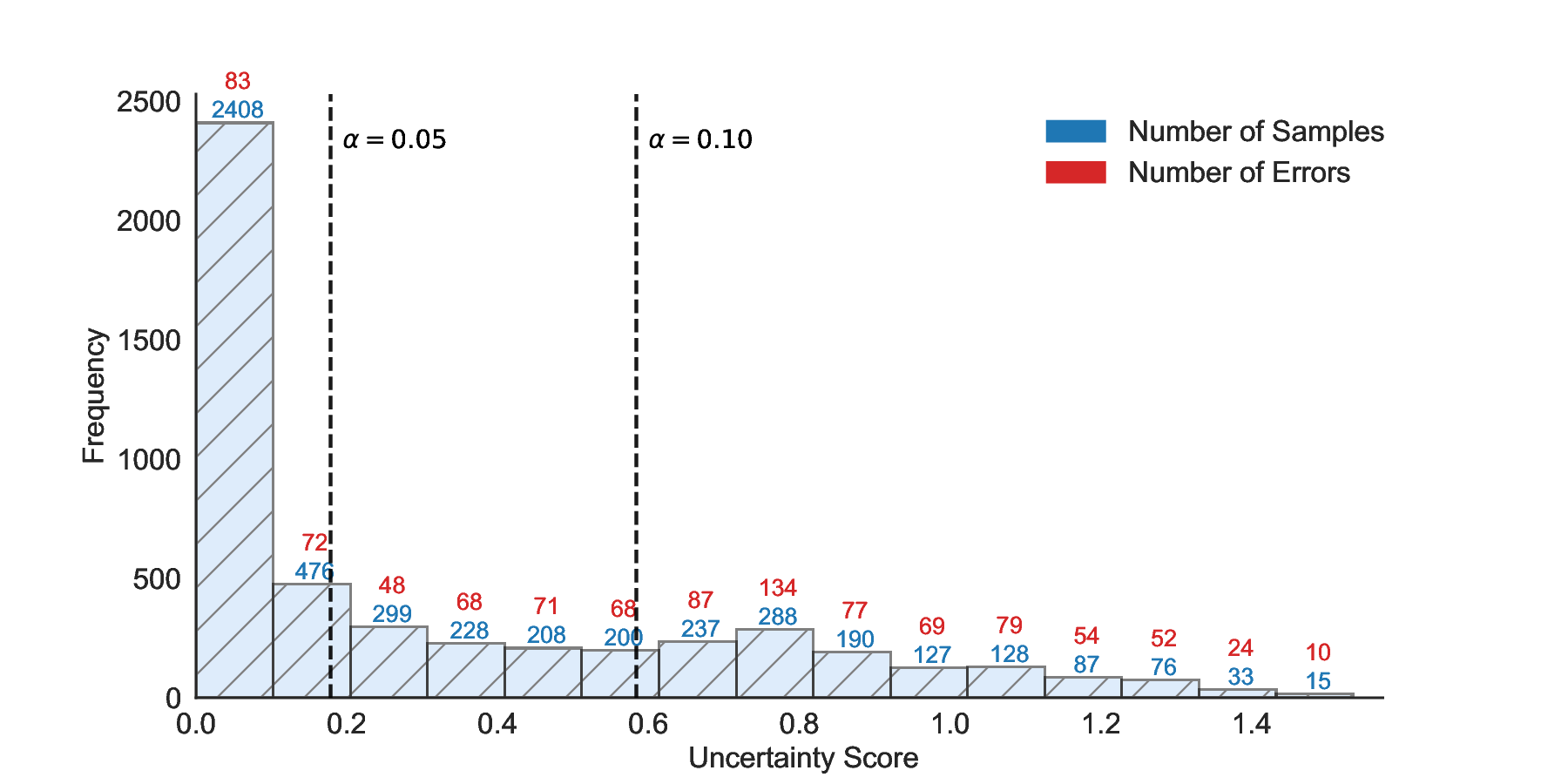
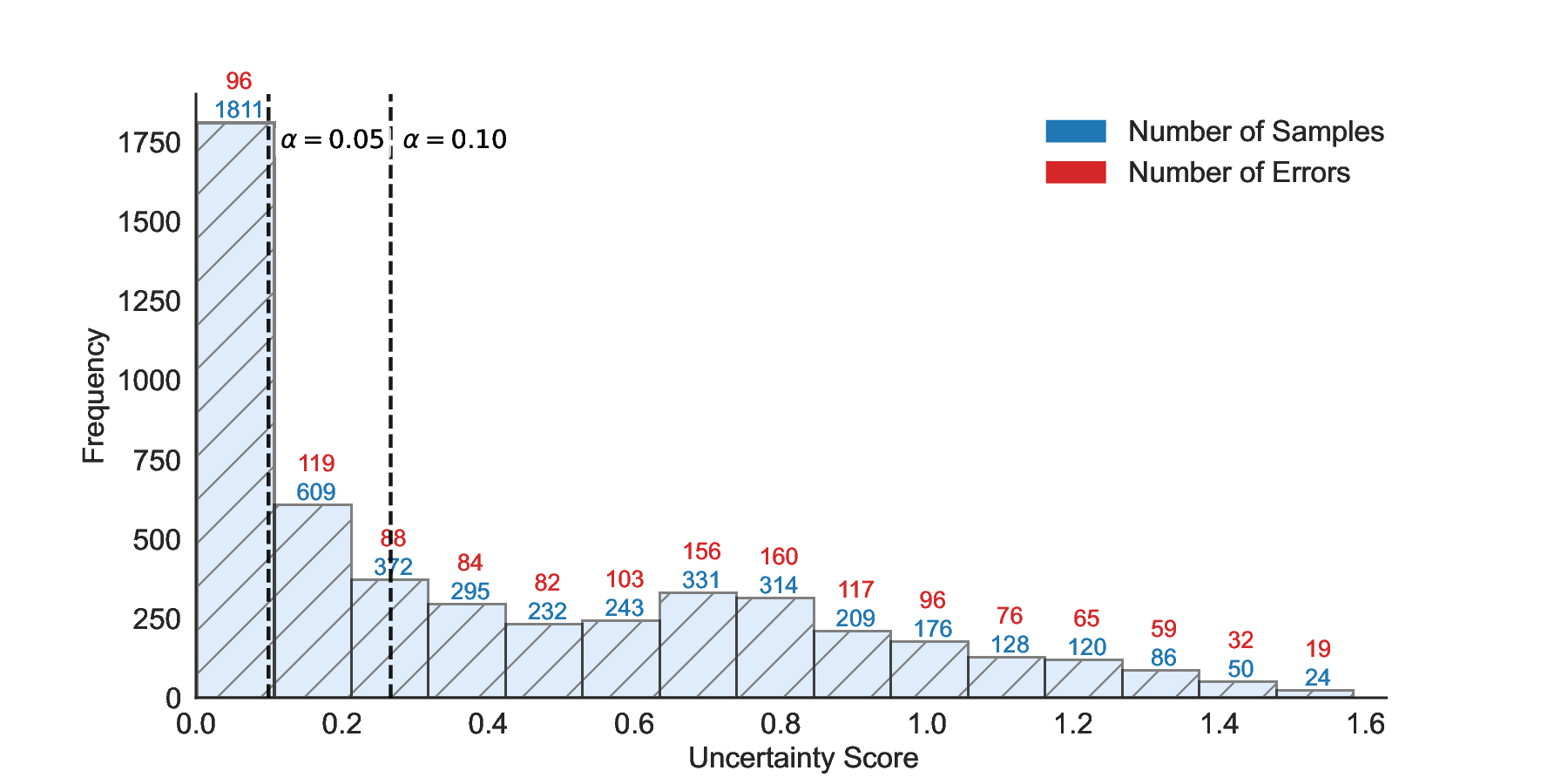
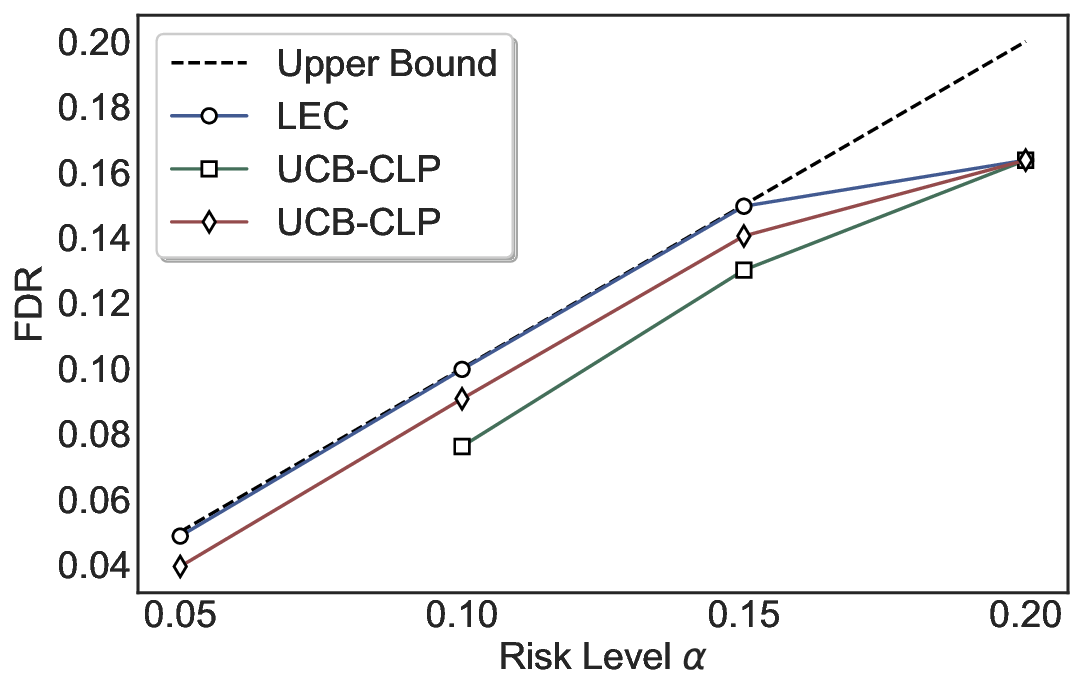
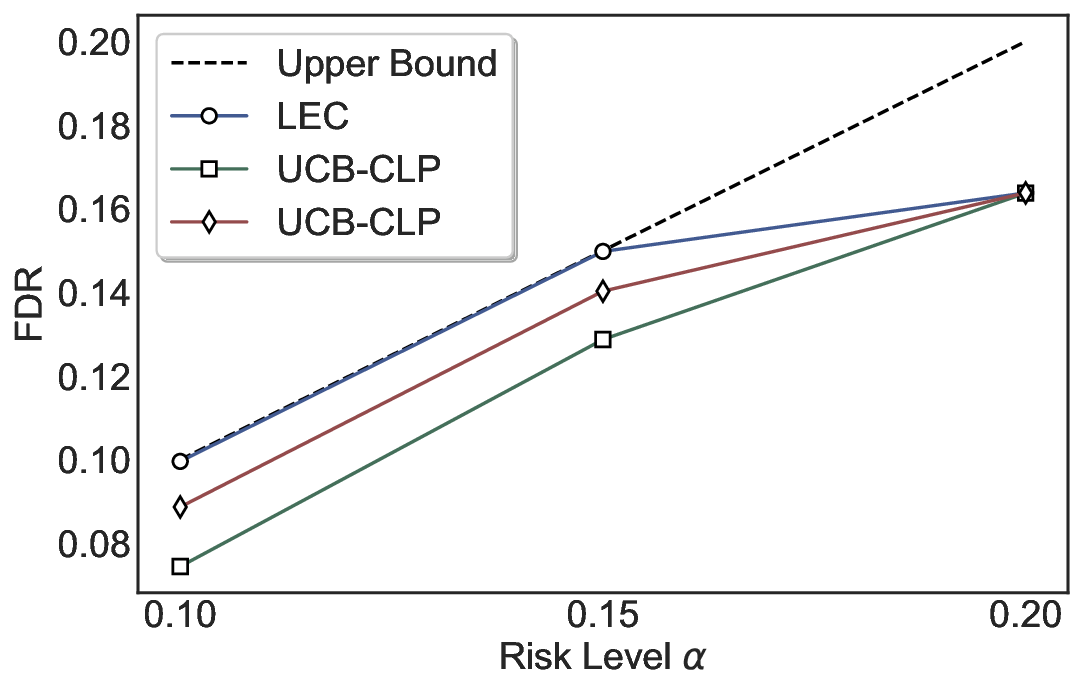
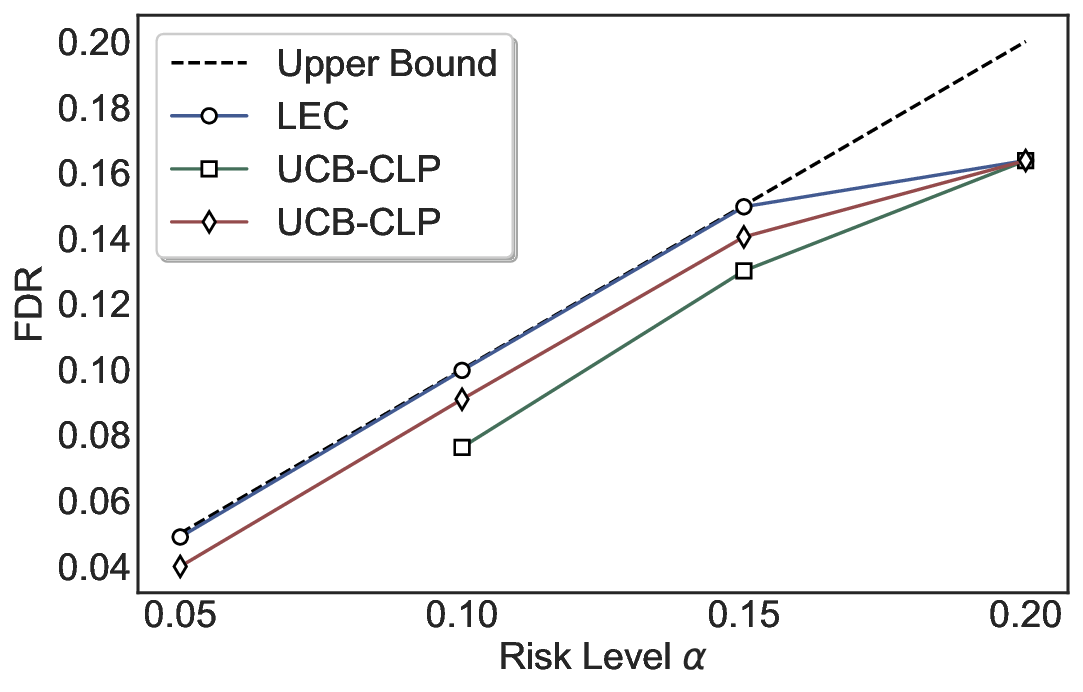
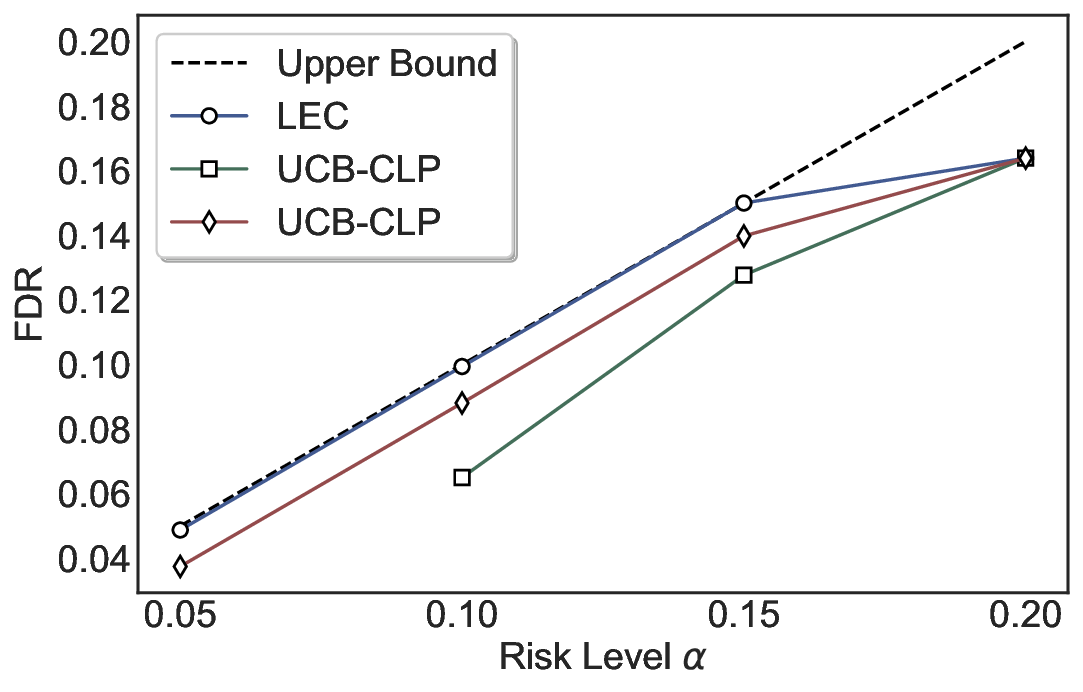
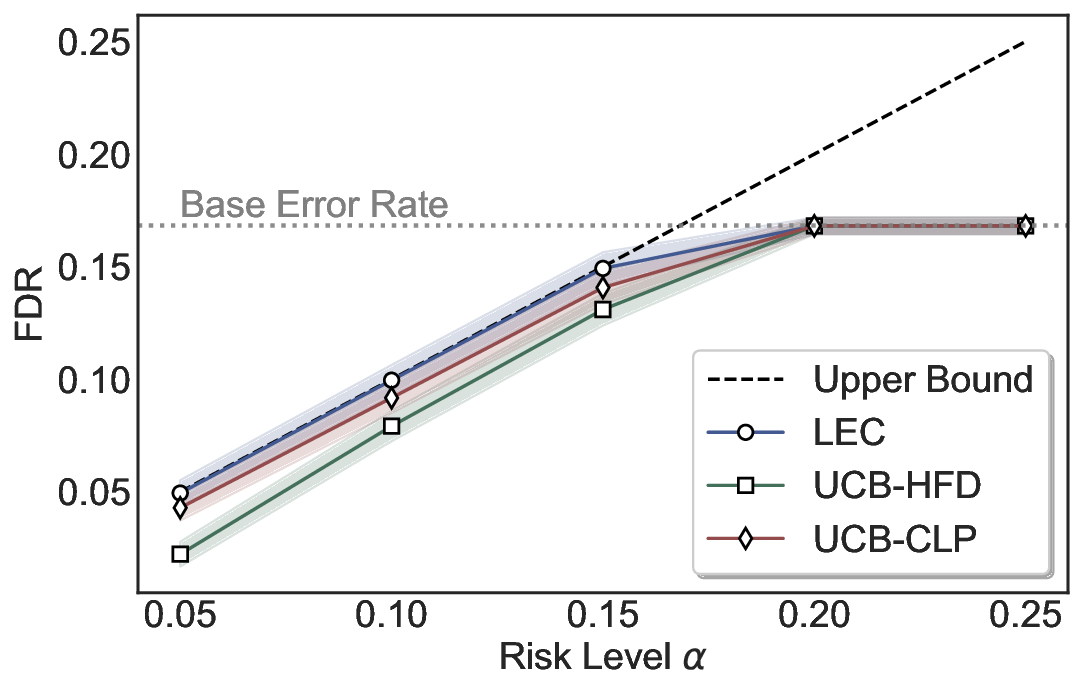
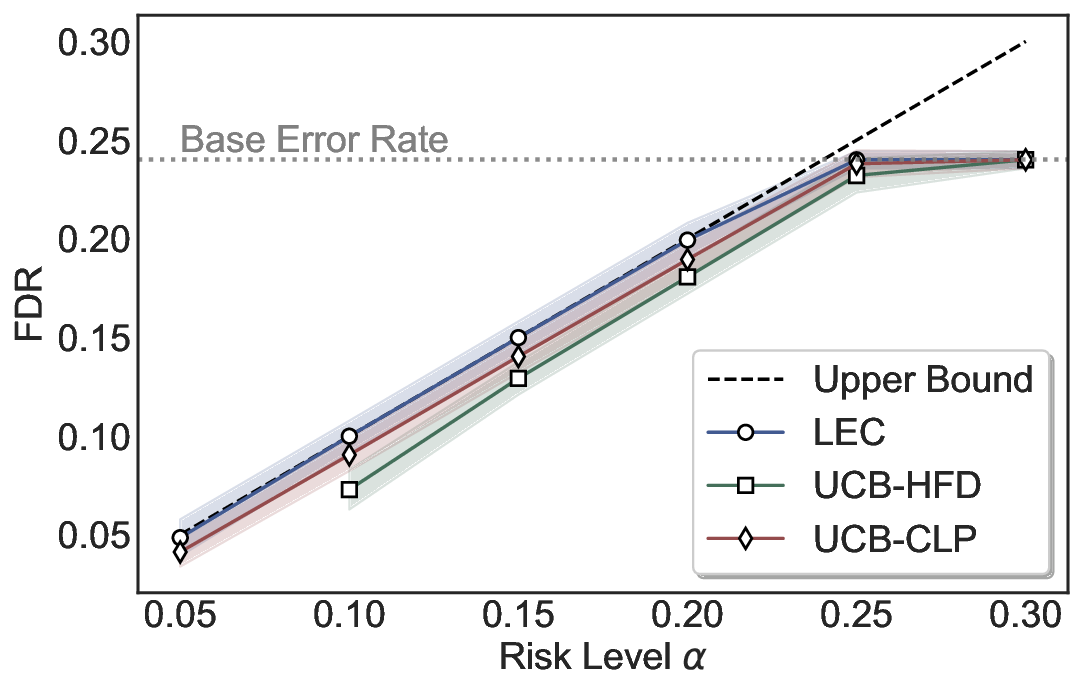
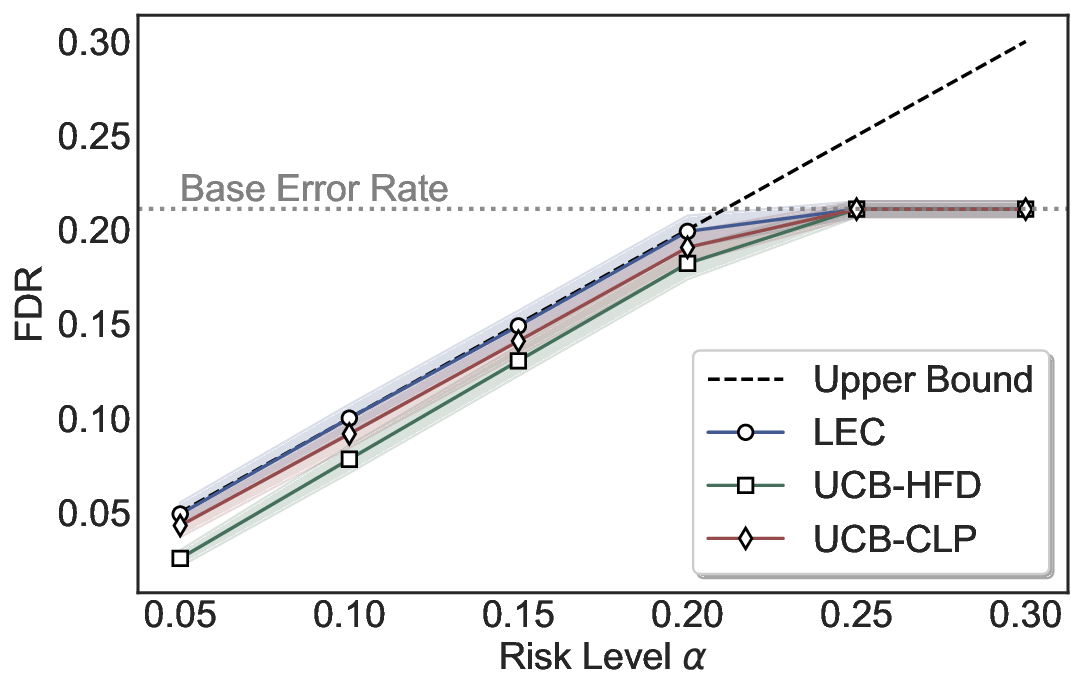
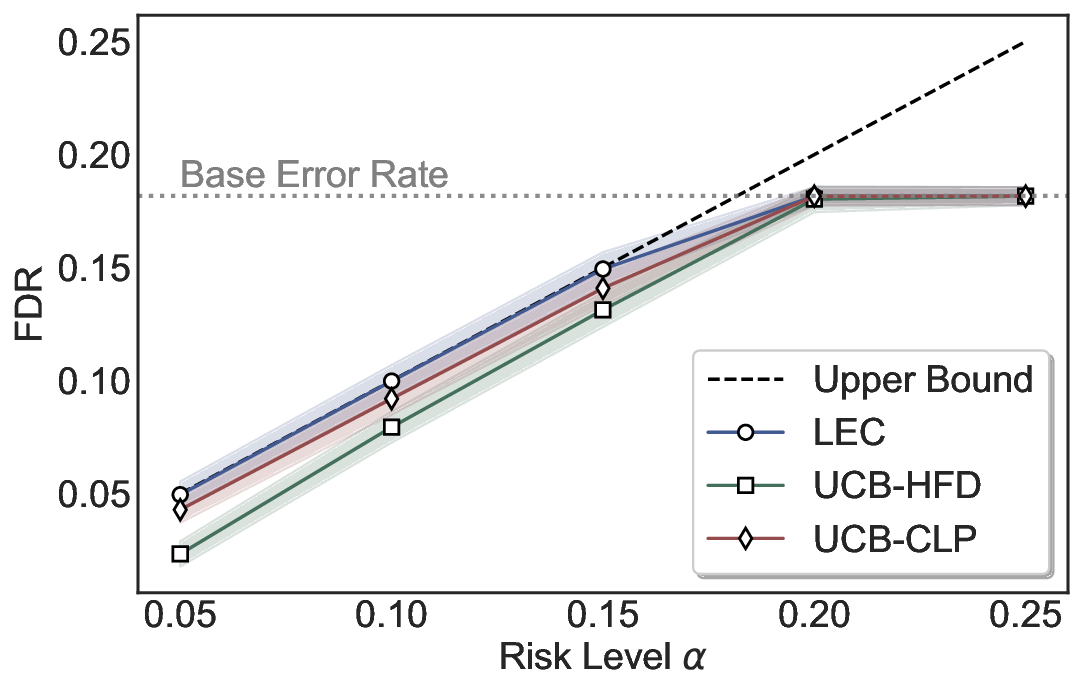
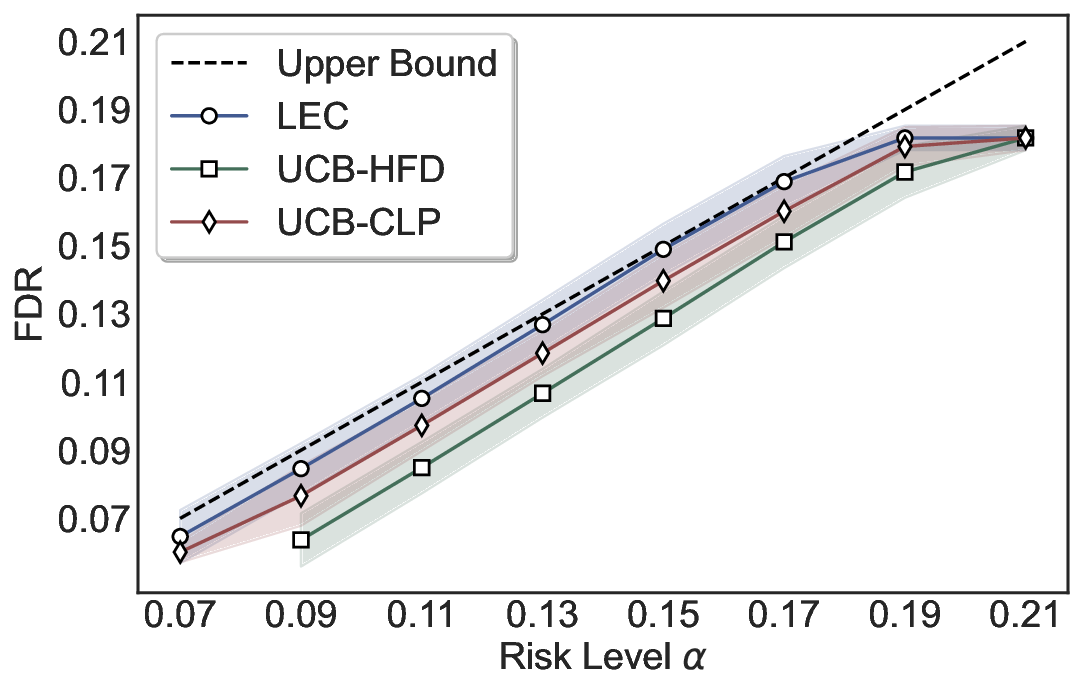
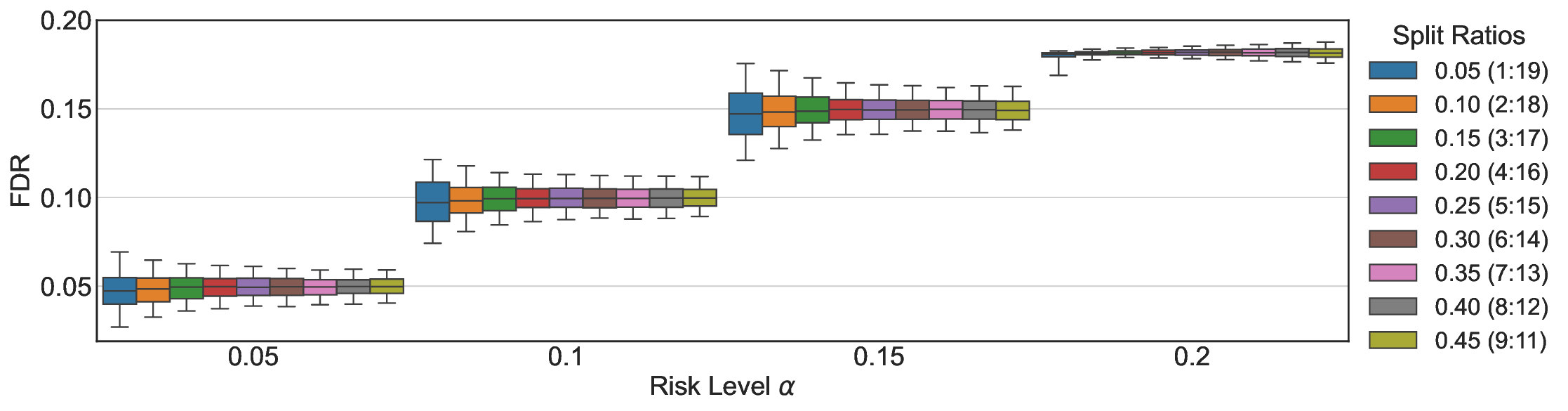
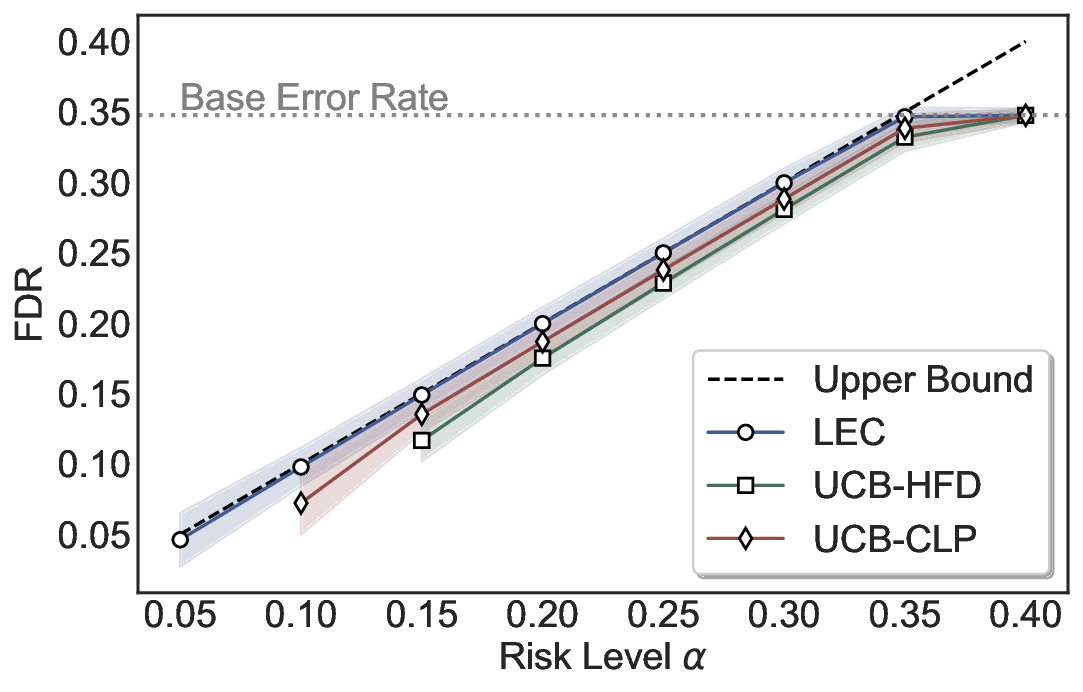
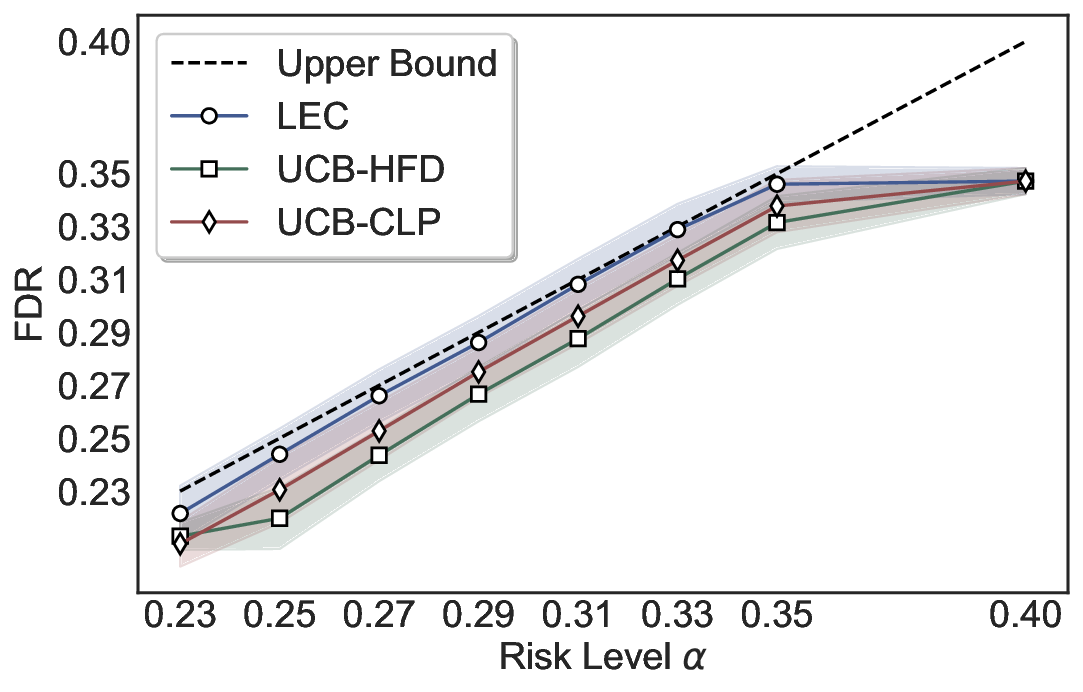
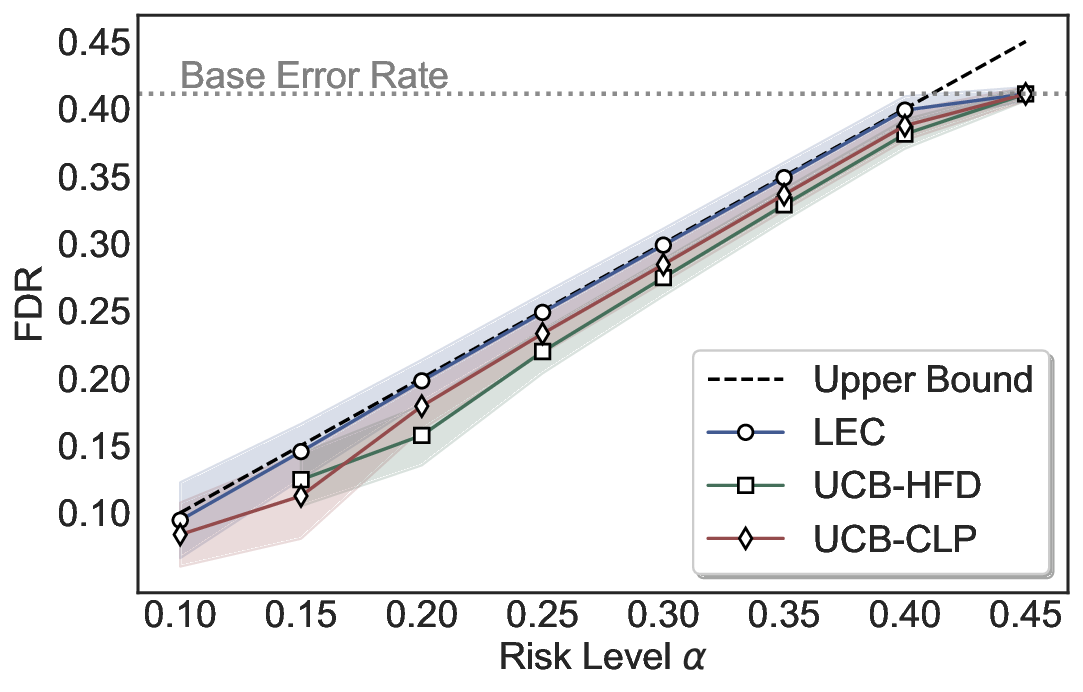
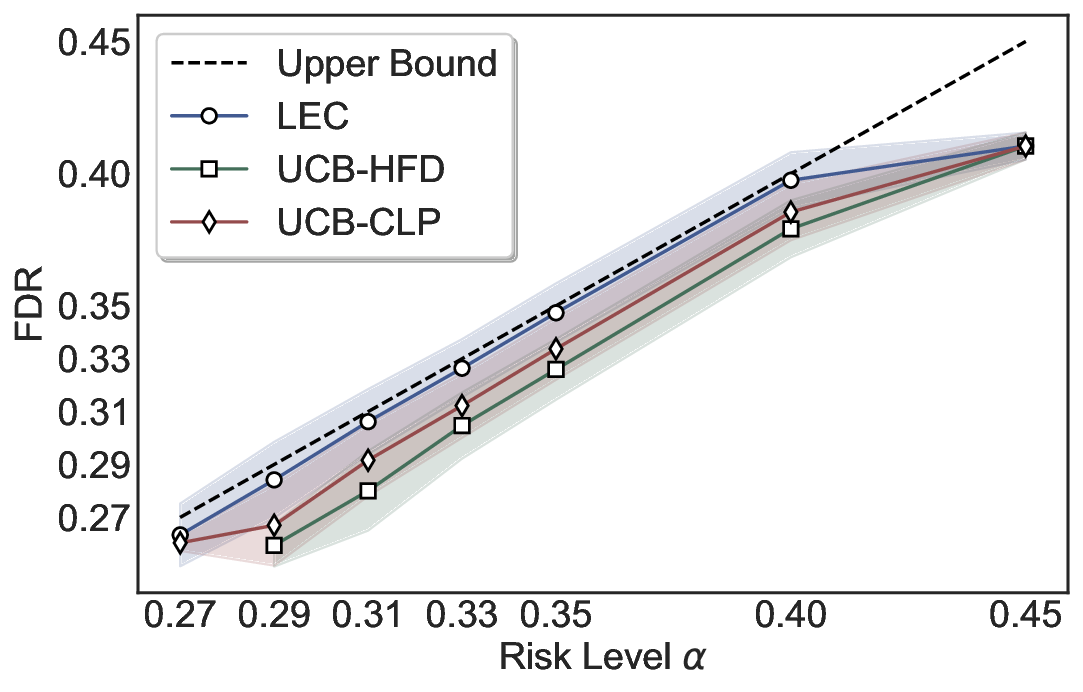
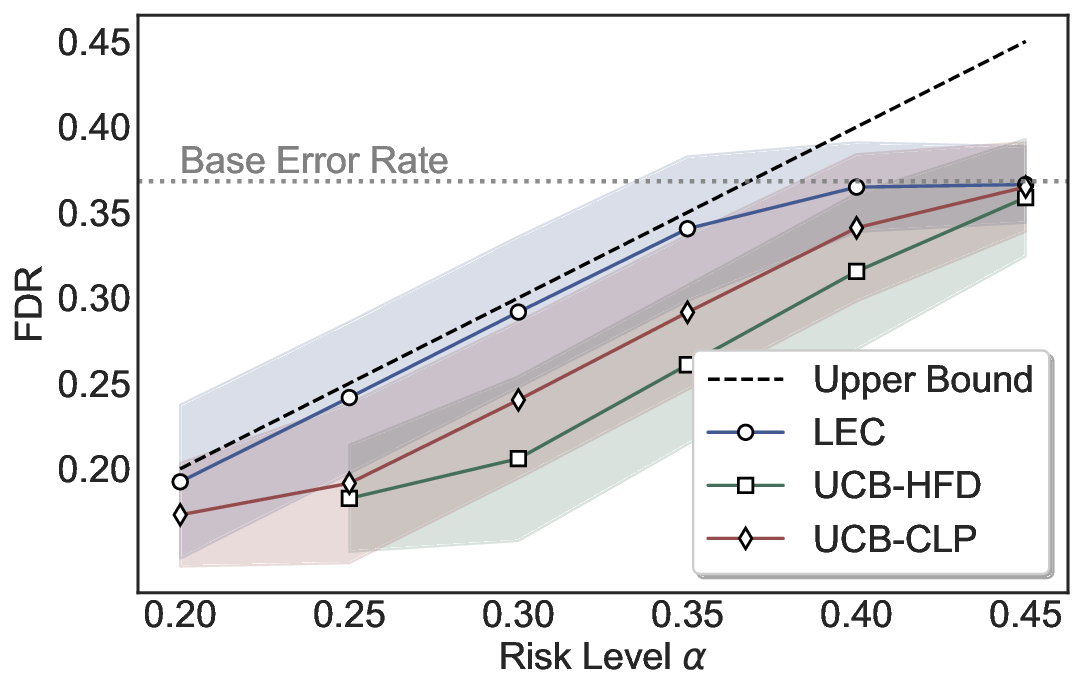
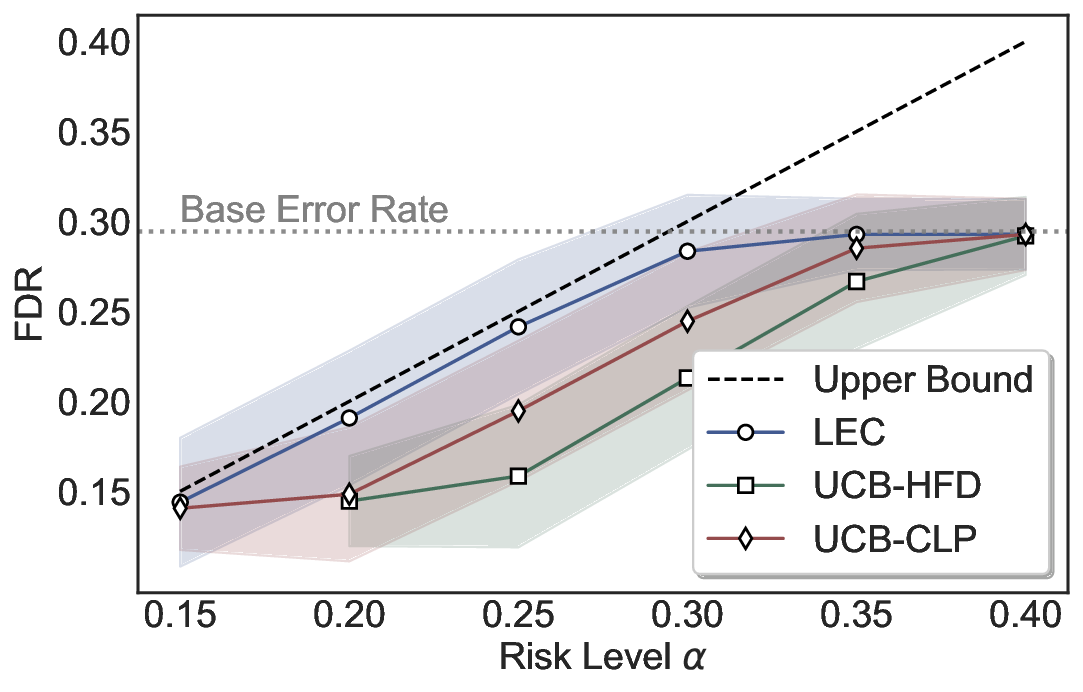
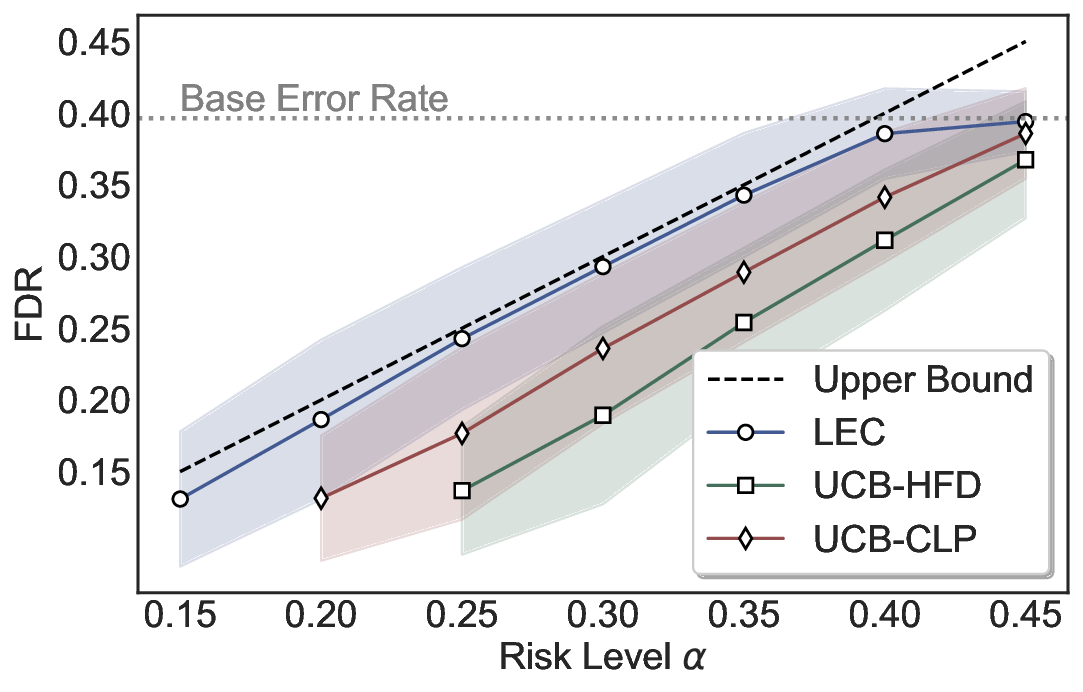
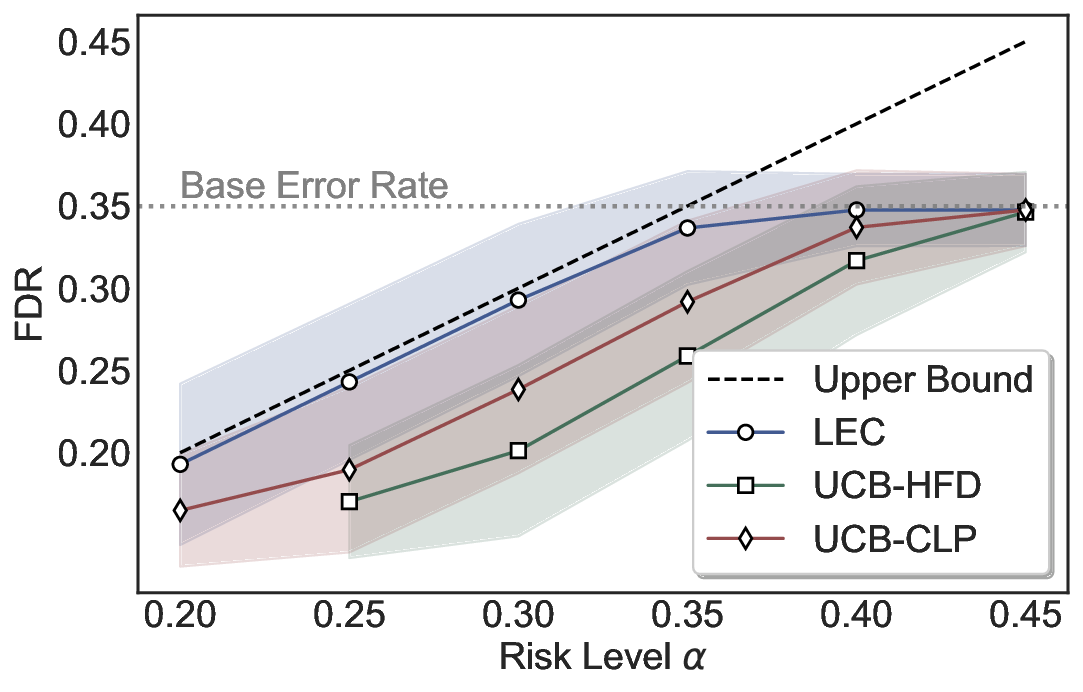
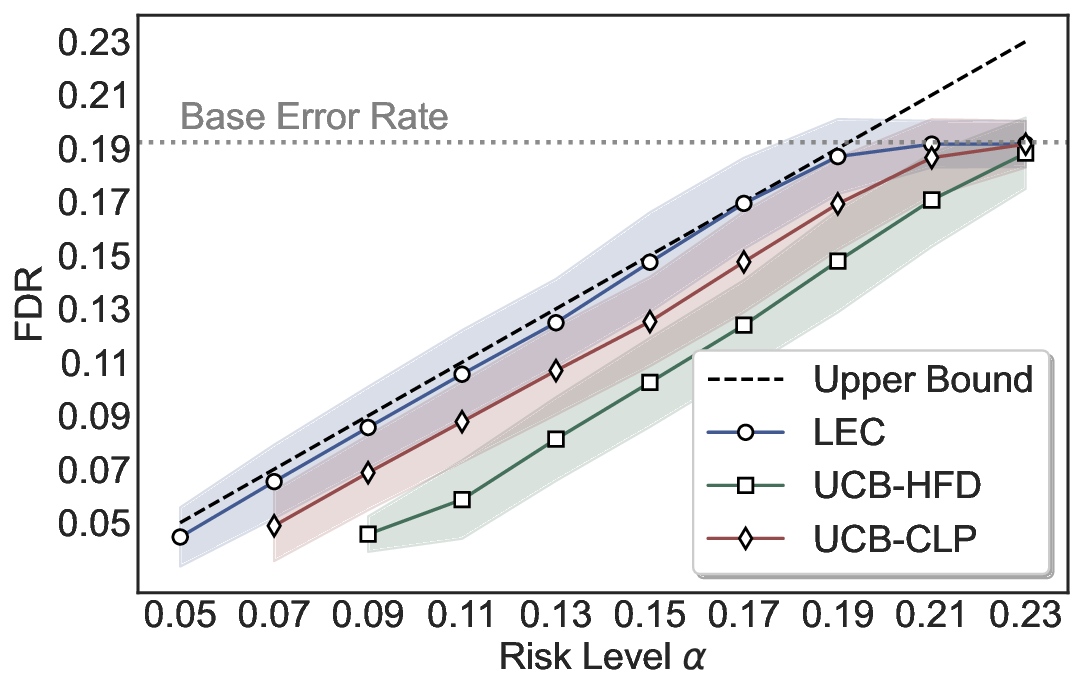
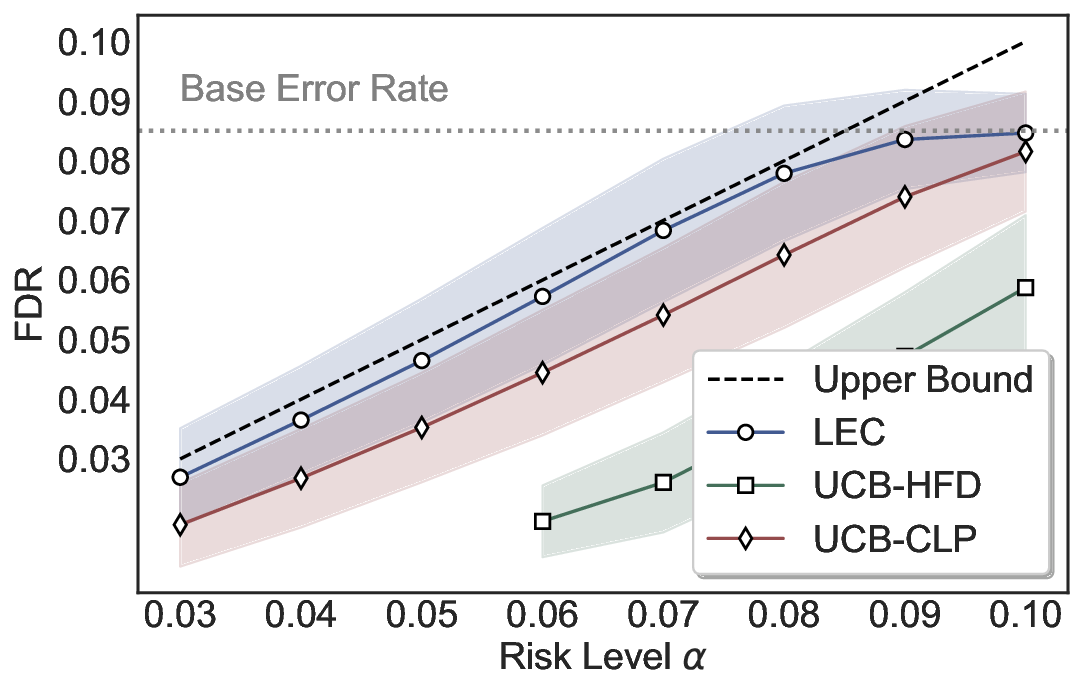
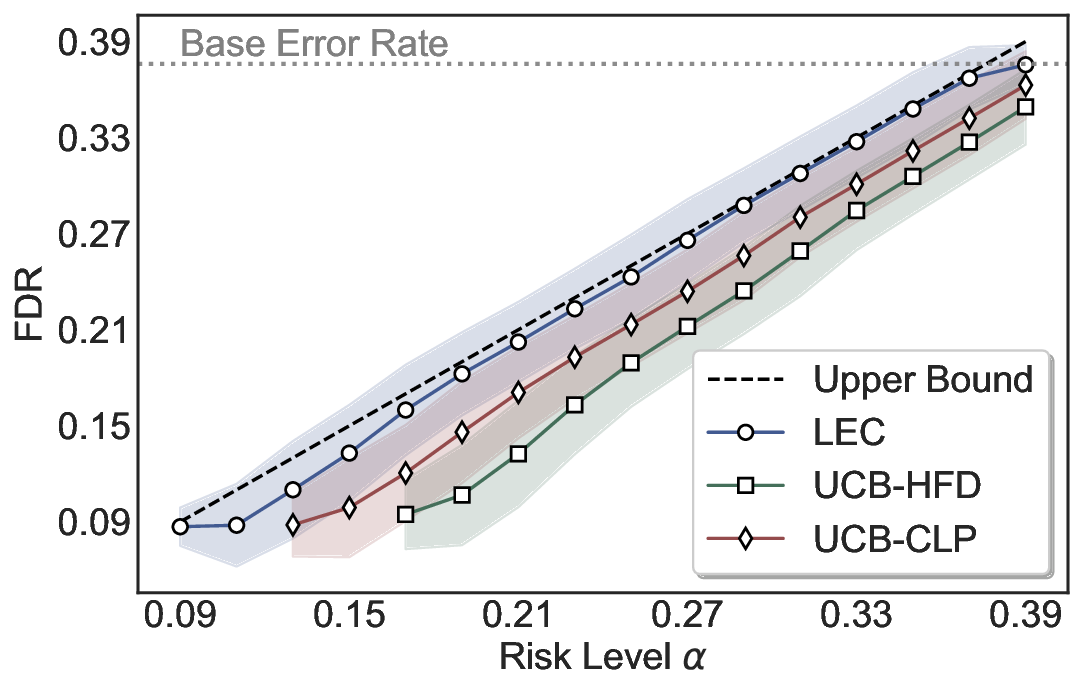
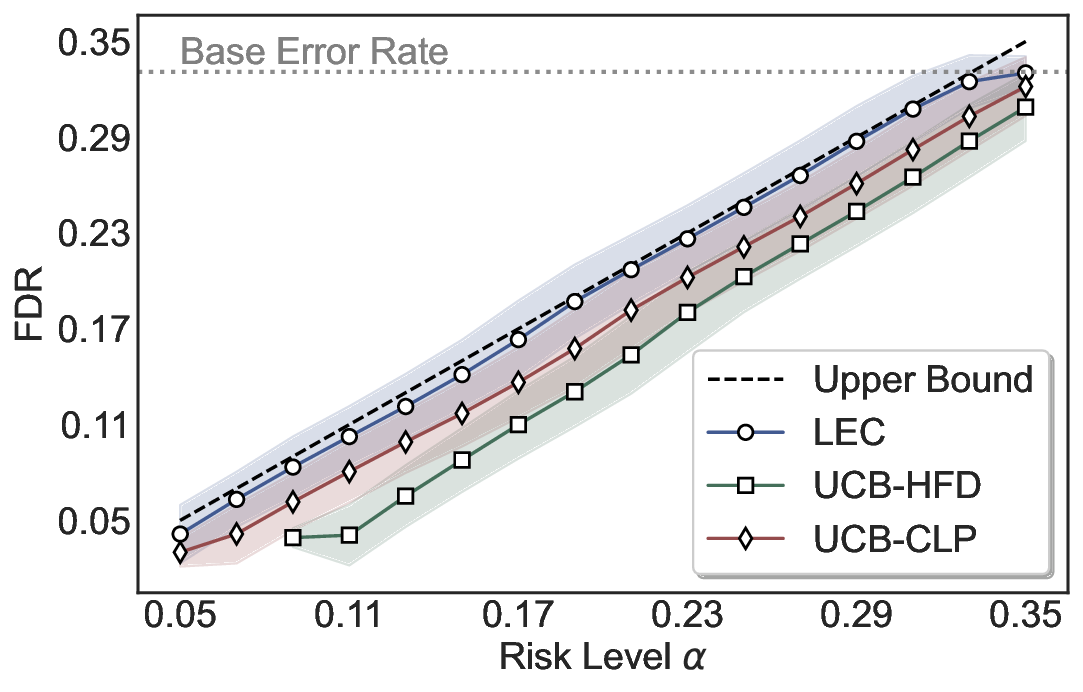
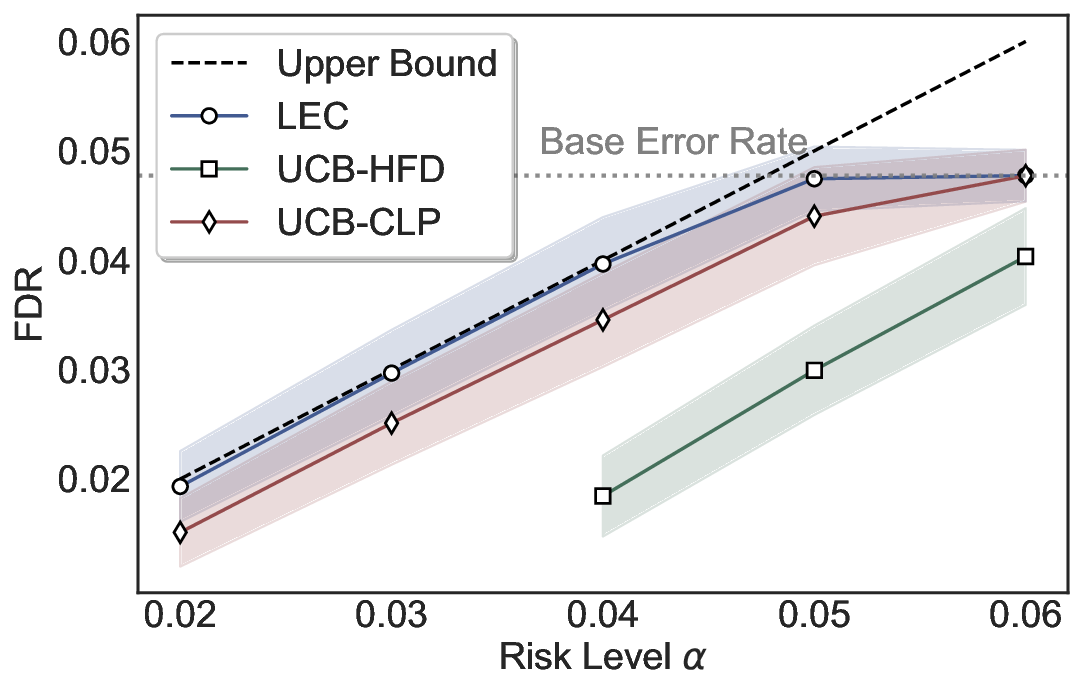
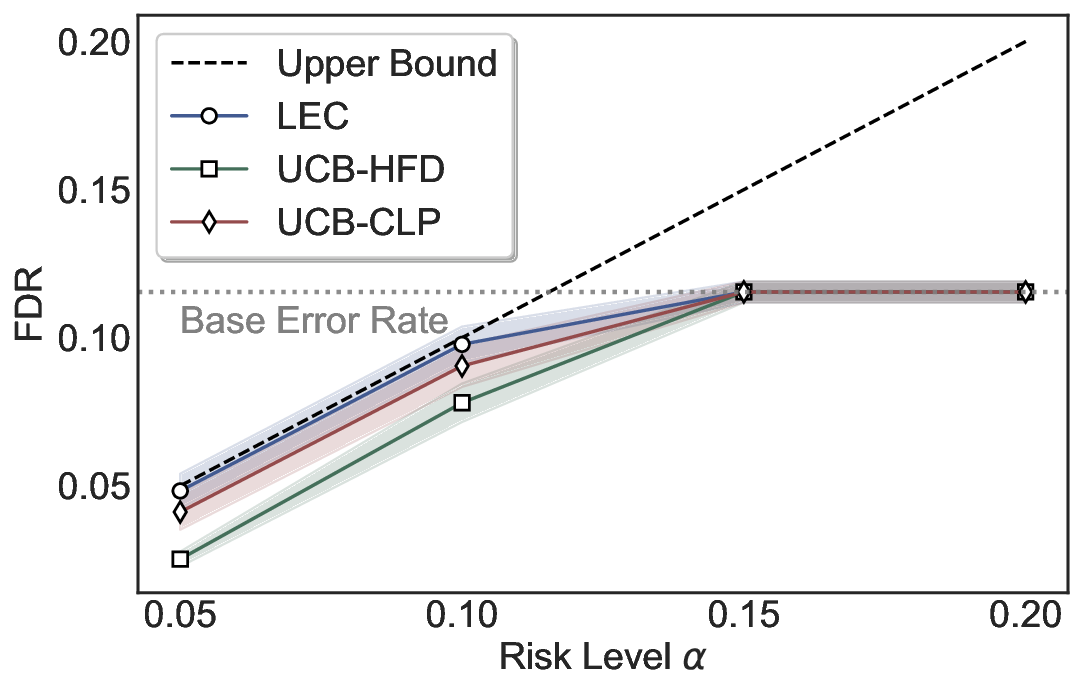
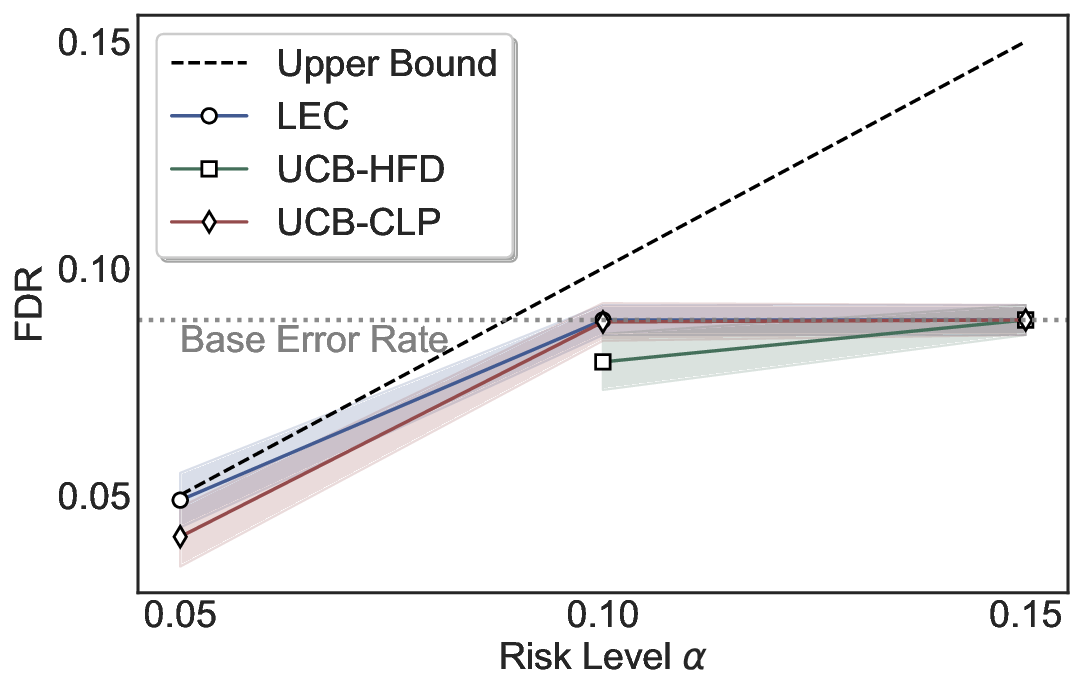
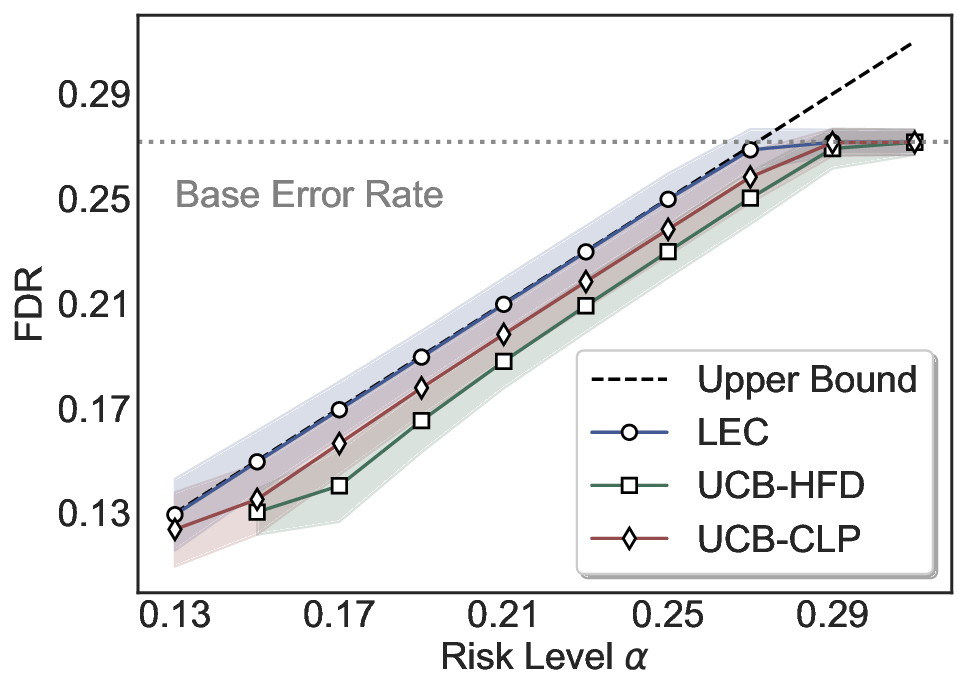
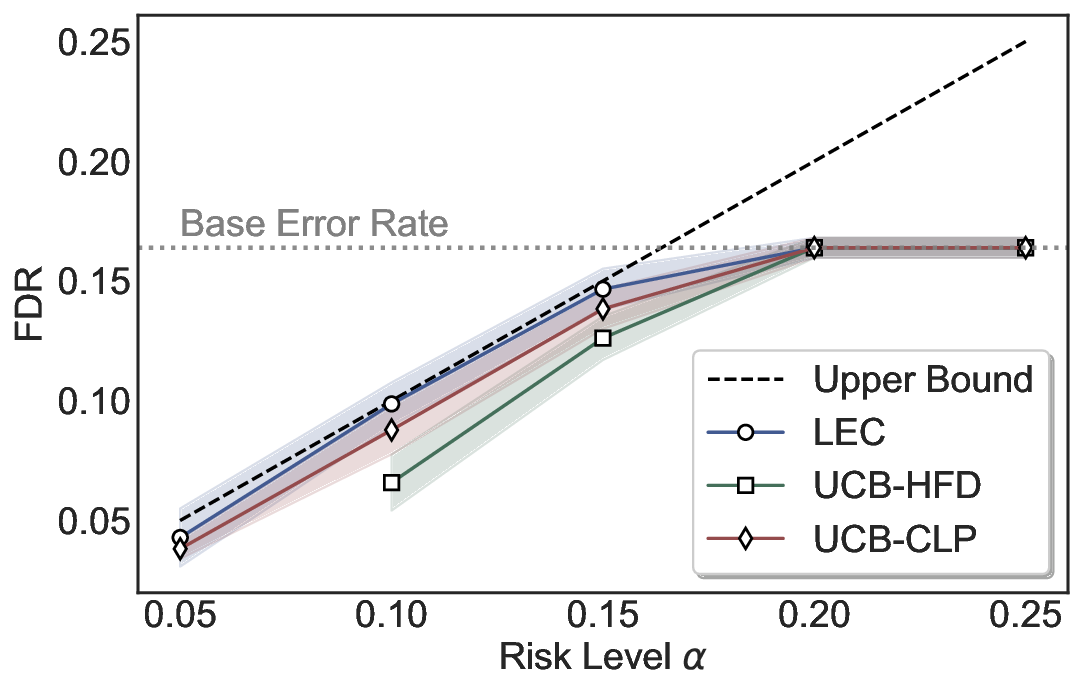
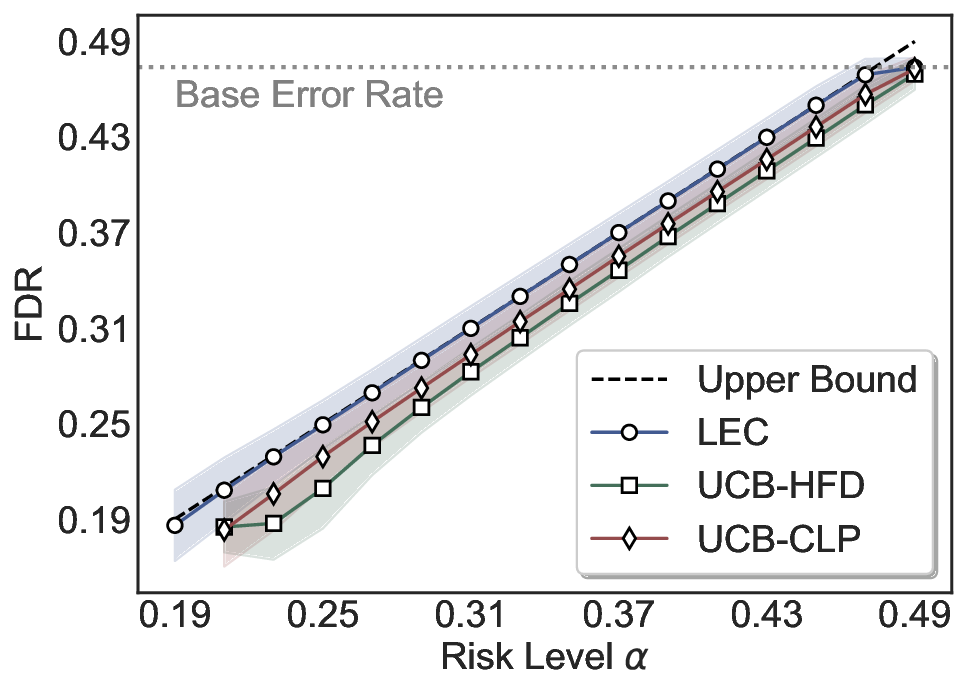
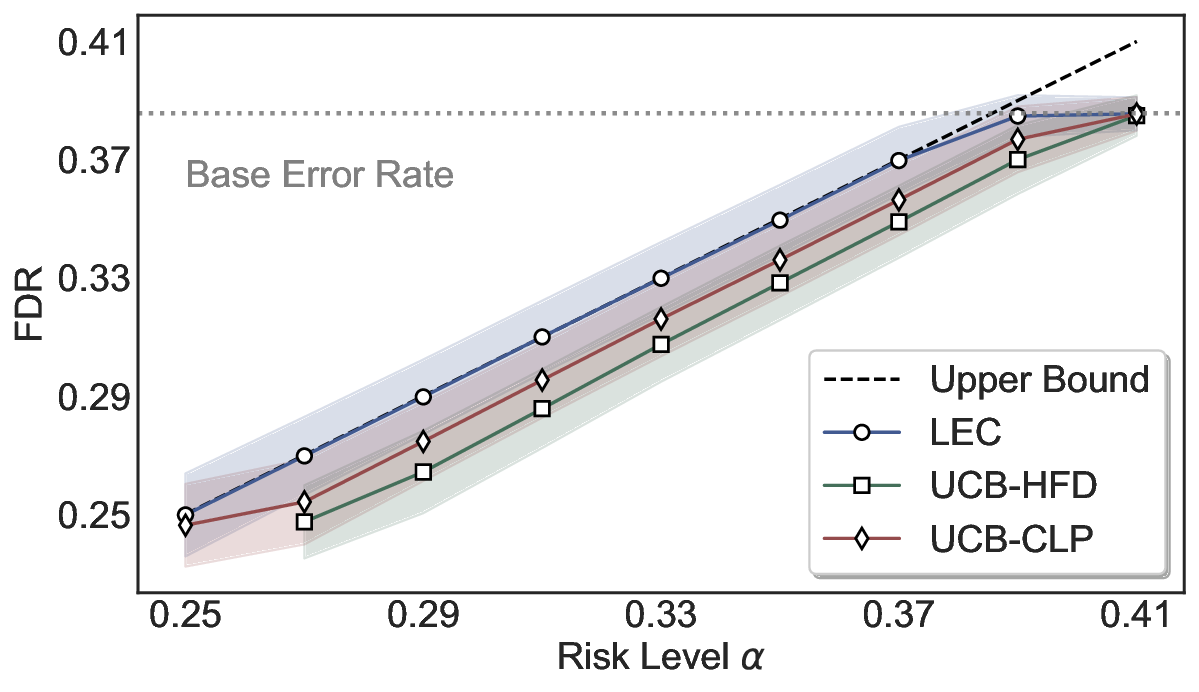
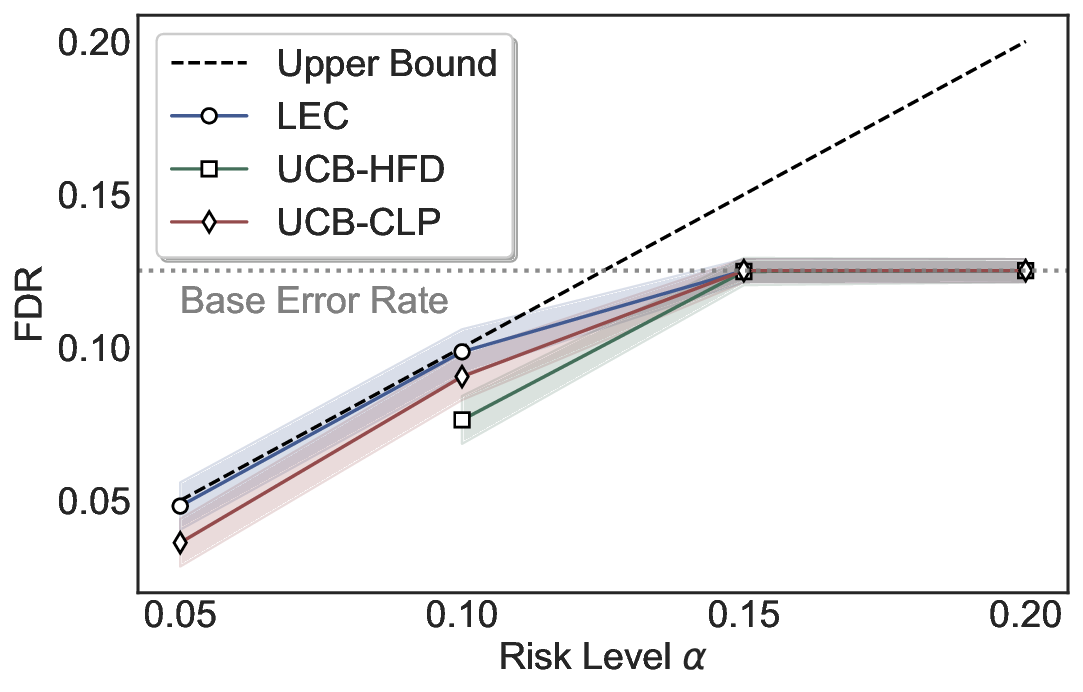
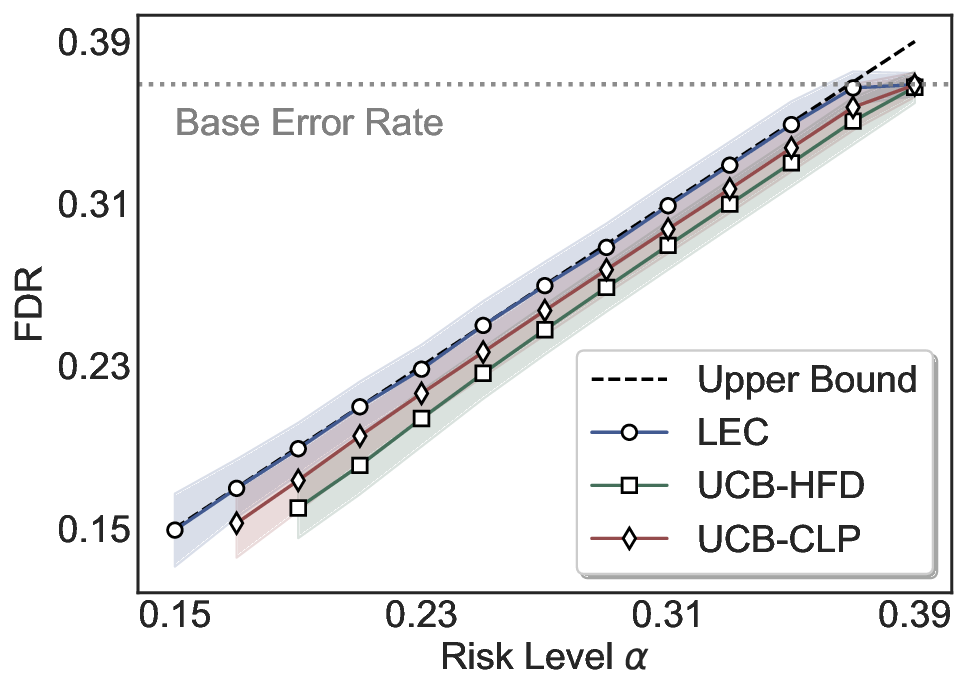
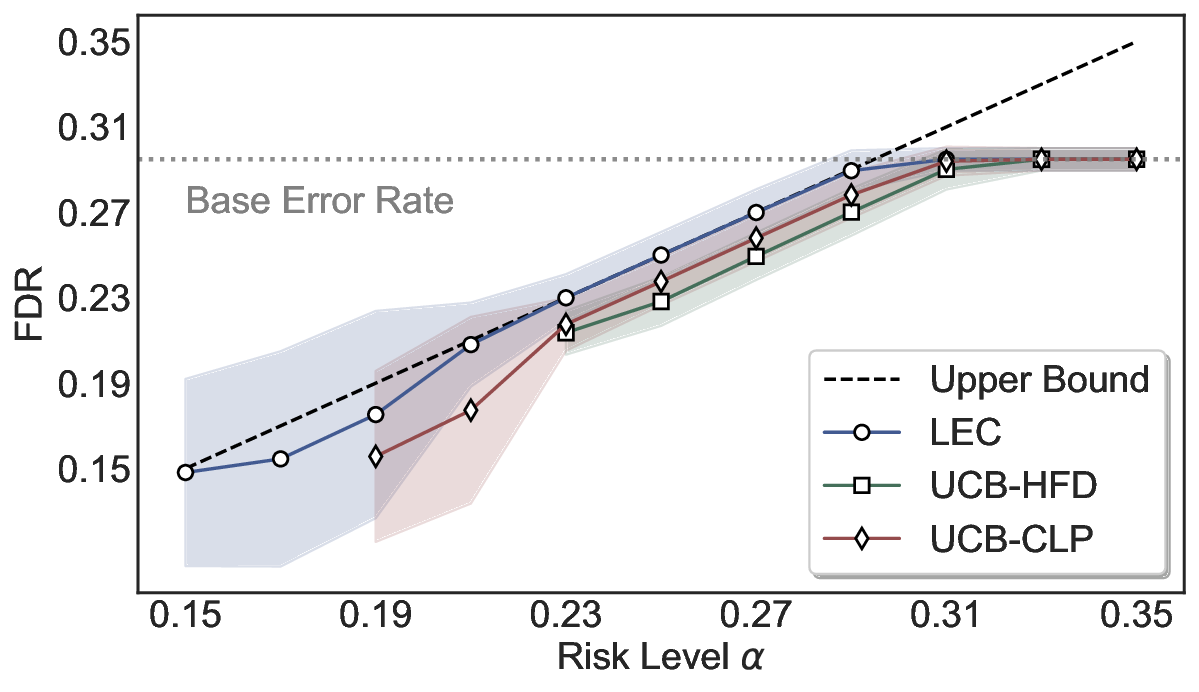
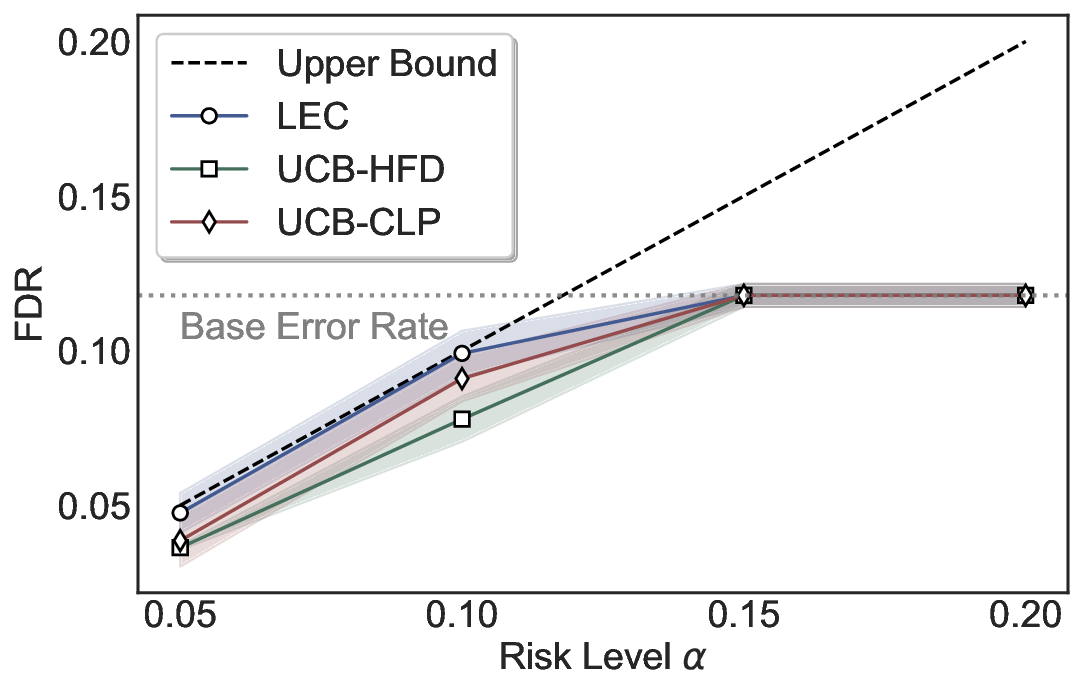
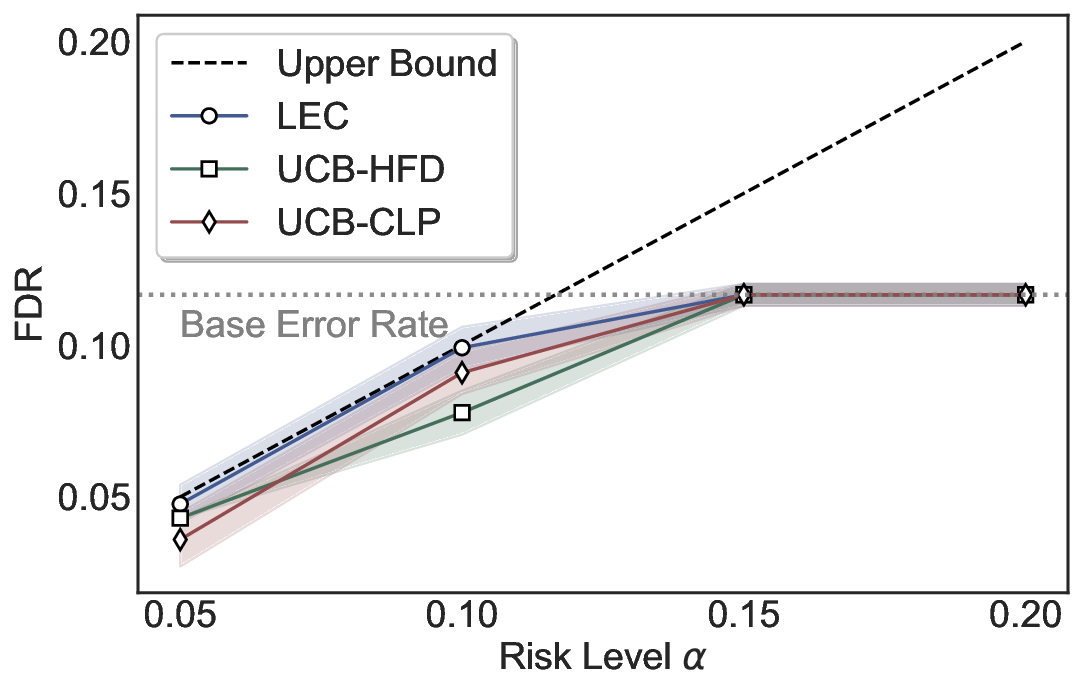
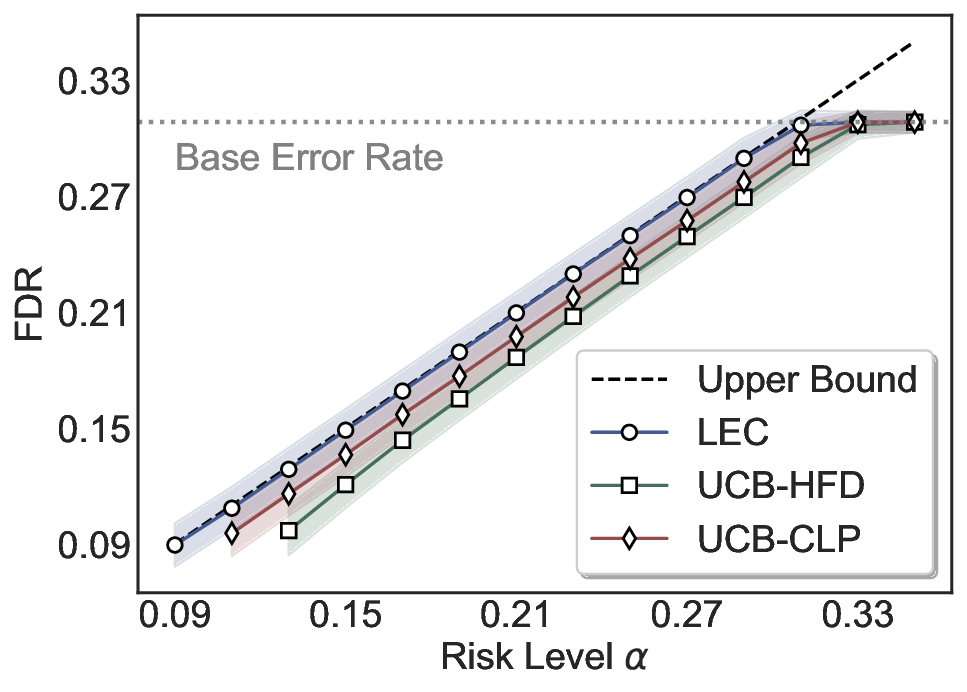
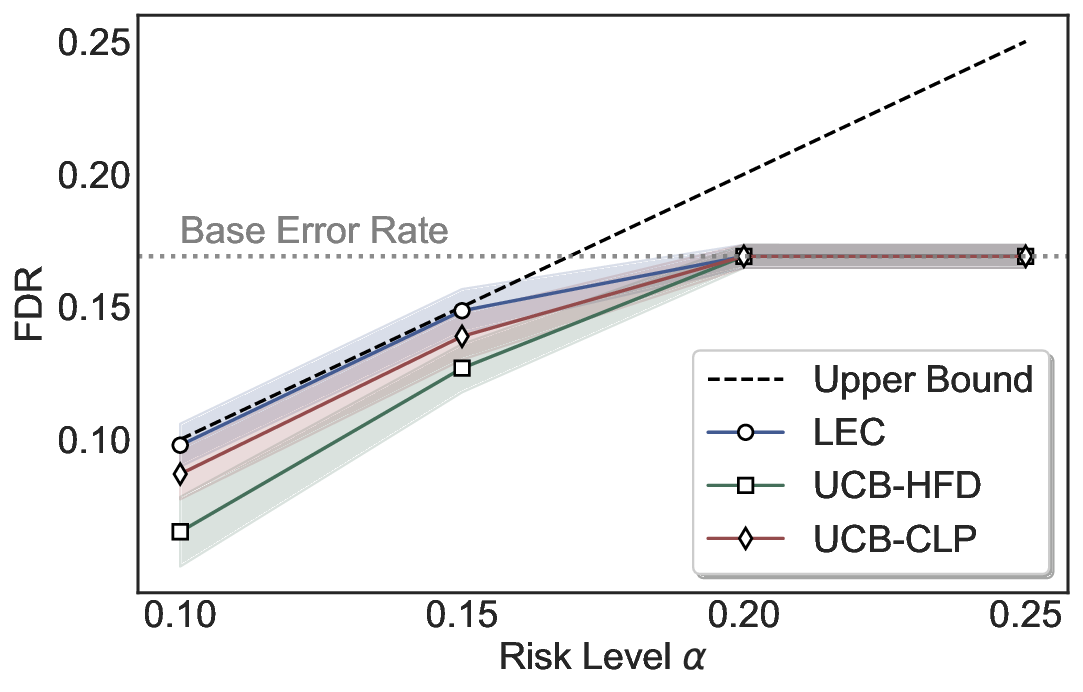
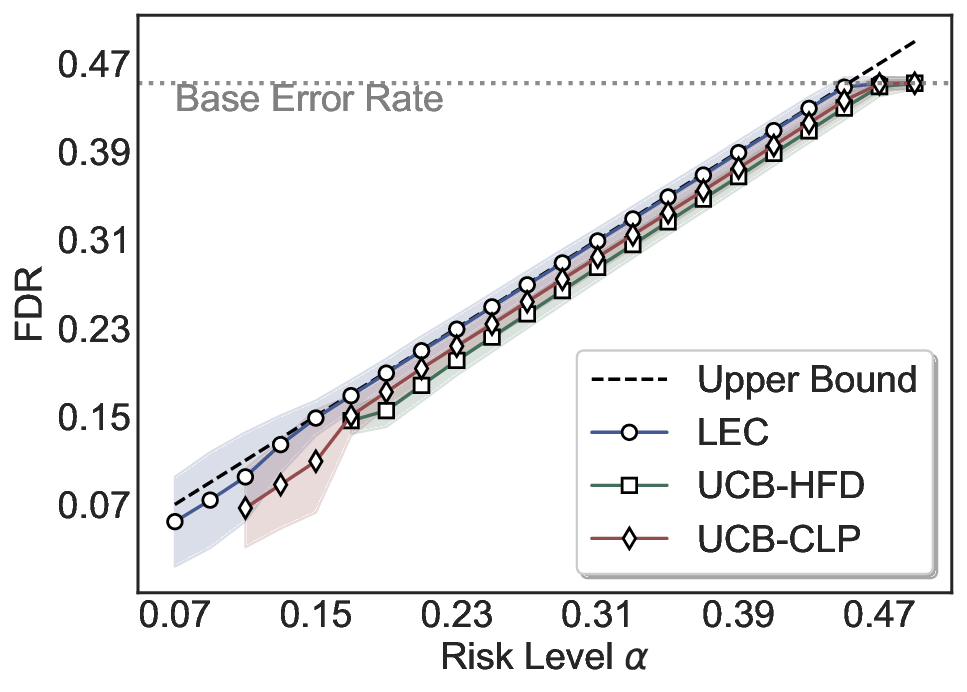
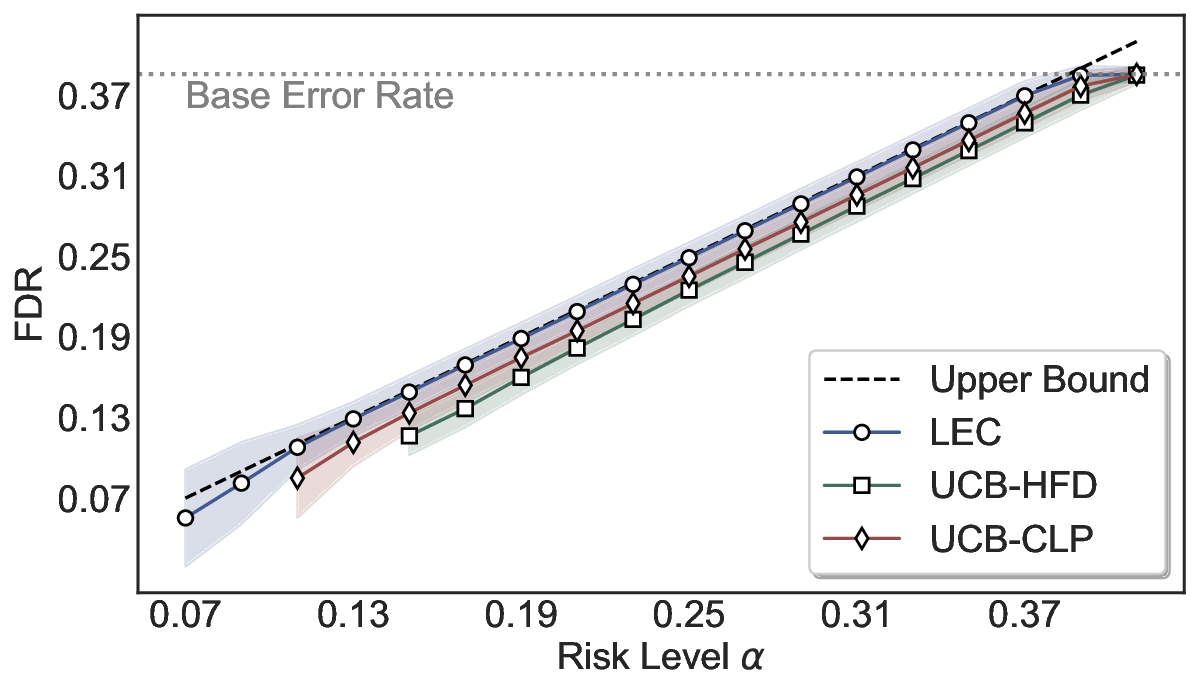
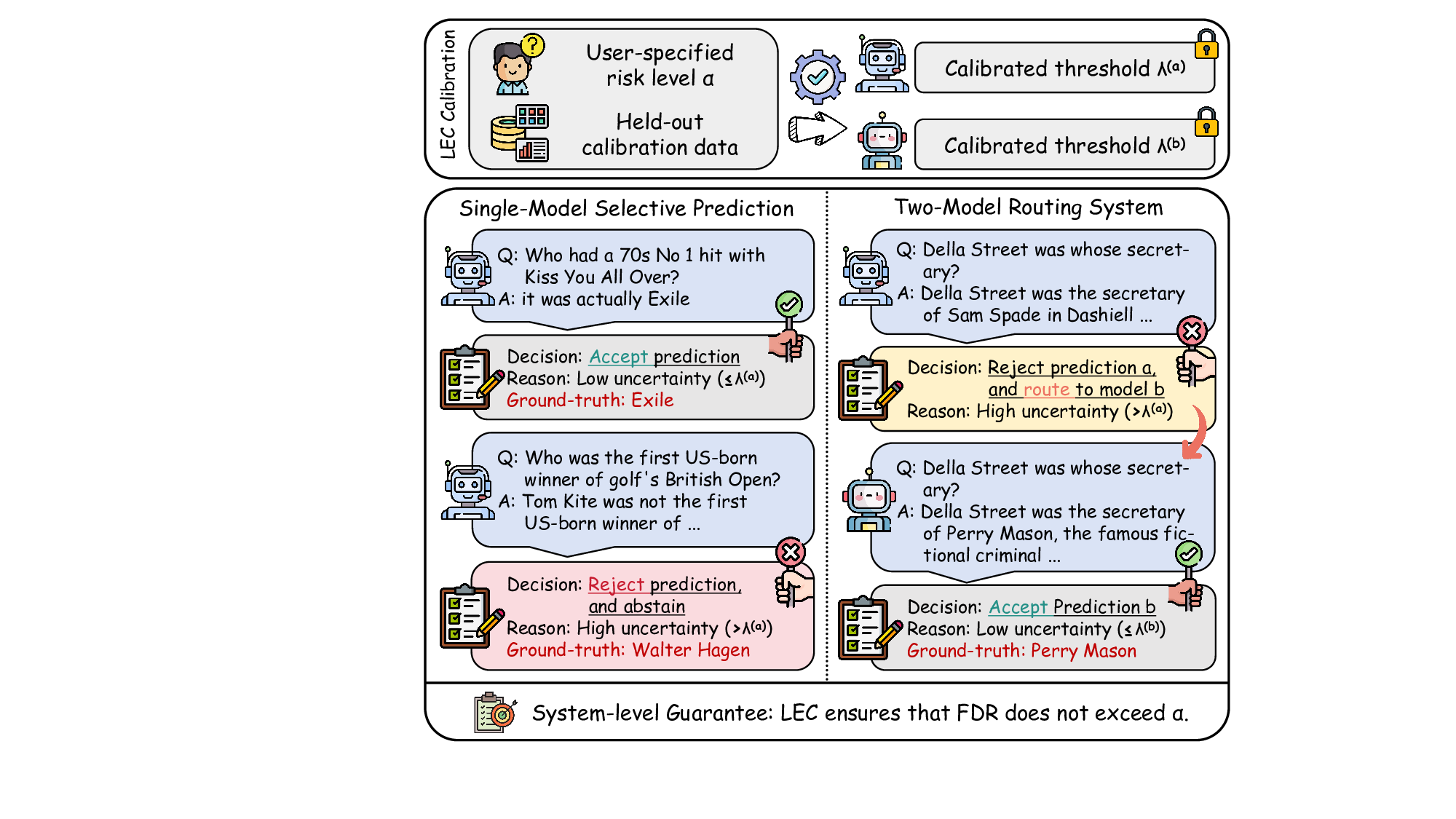
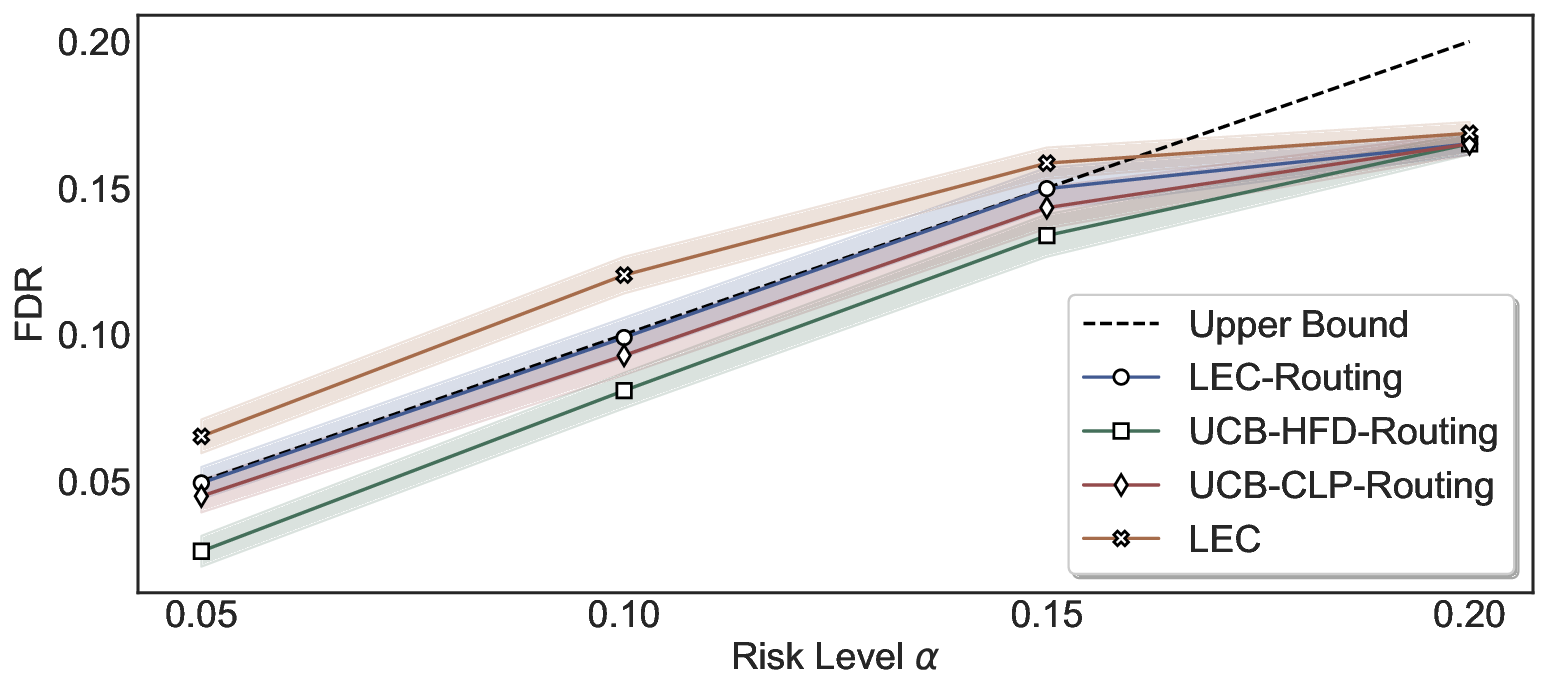
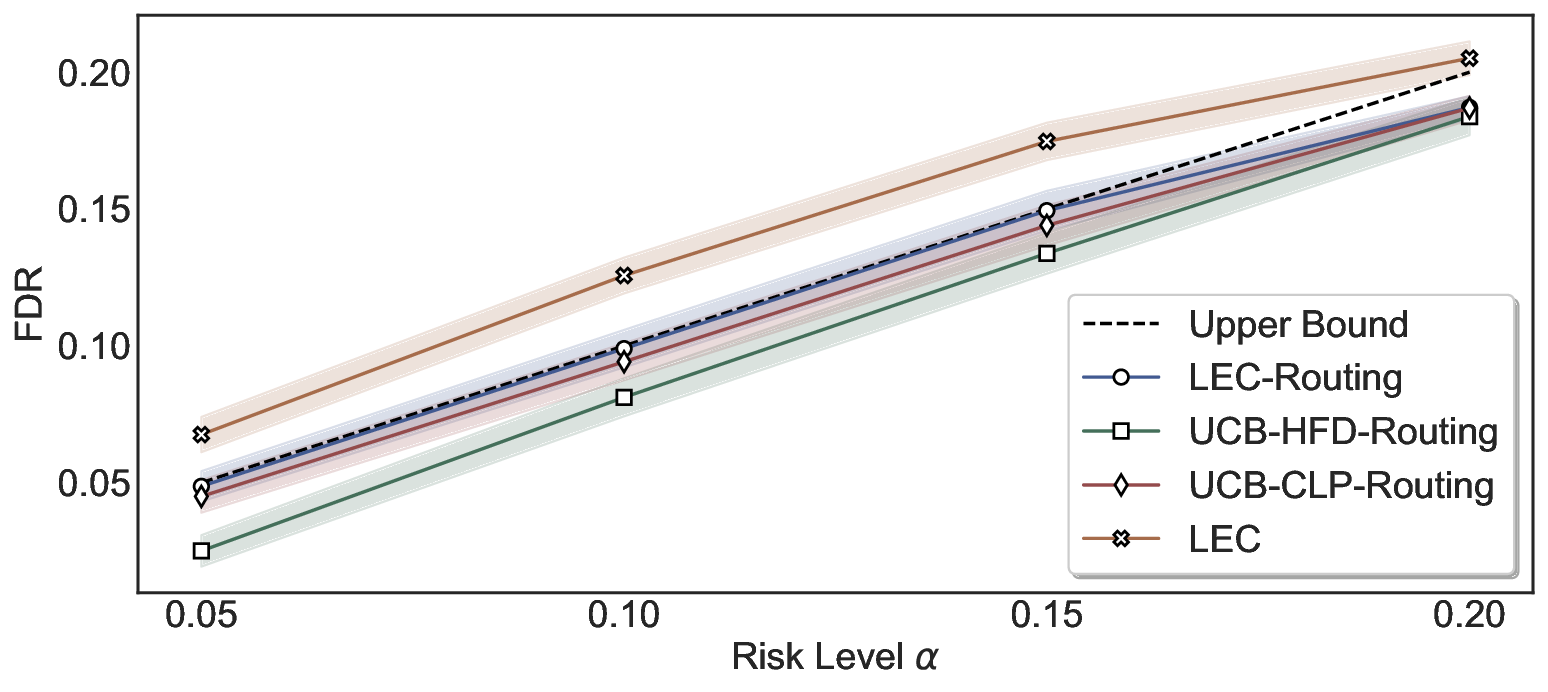
LEC(Linear Expectation Constraint) 프레임워크는 선택(prediction)과 오류(error) 두 이진 지표를 각각 0‑1 변수로 두고, 이들의 기대값 사이에 선형 제약을 부과한다. 구체적으로, 선택된 샘플의 평균 오류율이 목표 FDR보다 작거나 같도록 하는 것이 핵심이다. 이 제약은 전통적인 “임계값 기반 선택”을 일반화한 형태이며, 보정 데이터(즉, 모델이 훈련에 사용되지 않은 교환 가능한 검증 집합)만을 이용해 충분조건을 도출한다. 충분조건은 선택 확률과 오류 확률을 각각 추정한 뒤, 이들의 비율이 목표 FDR을 초과하지 않도록 하는 간단한 불등식 형태로 표현된다.
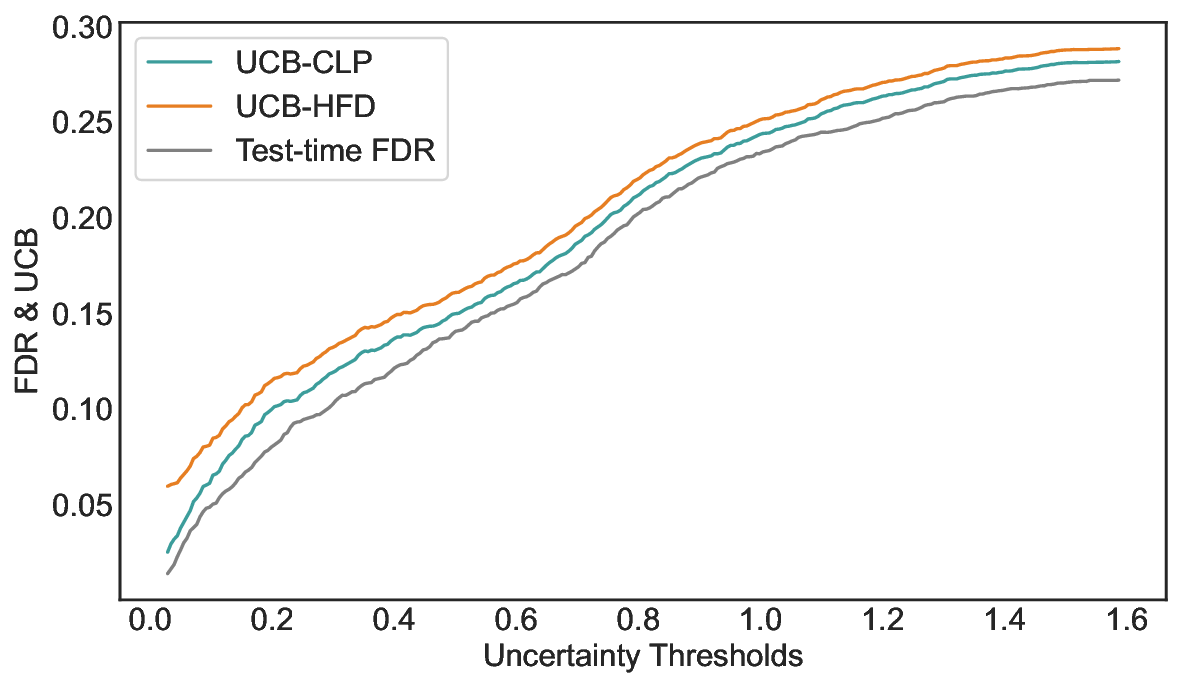
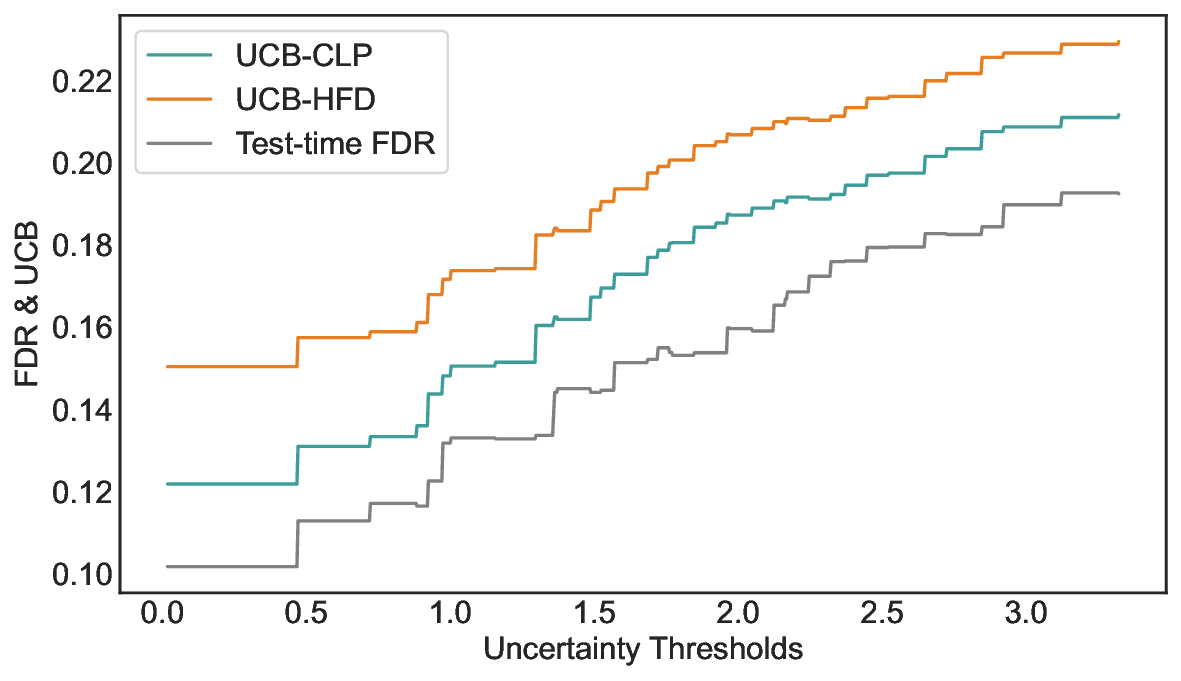
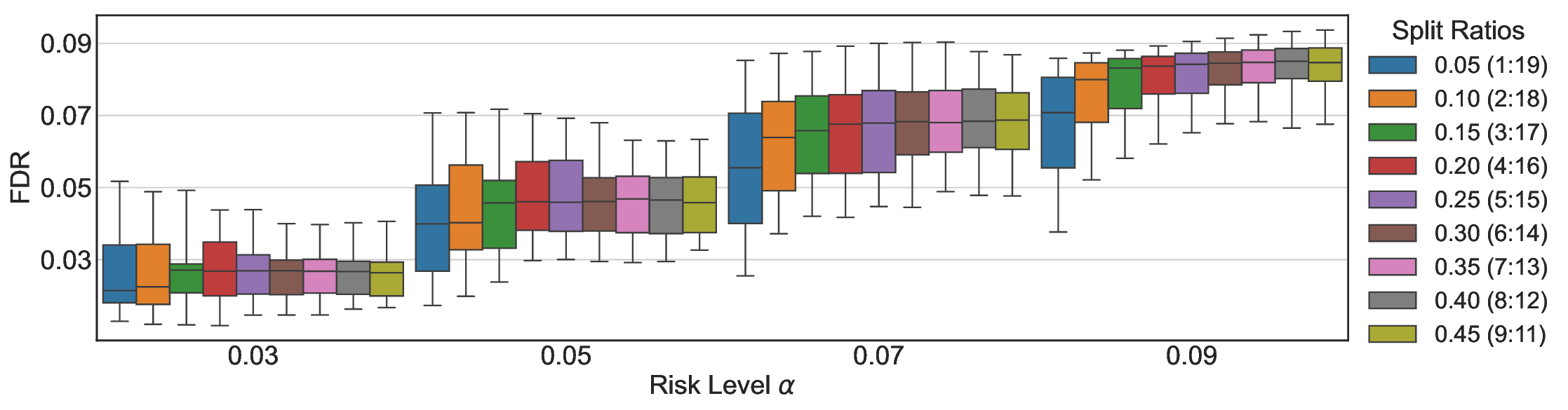
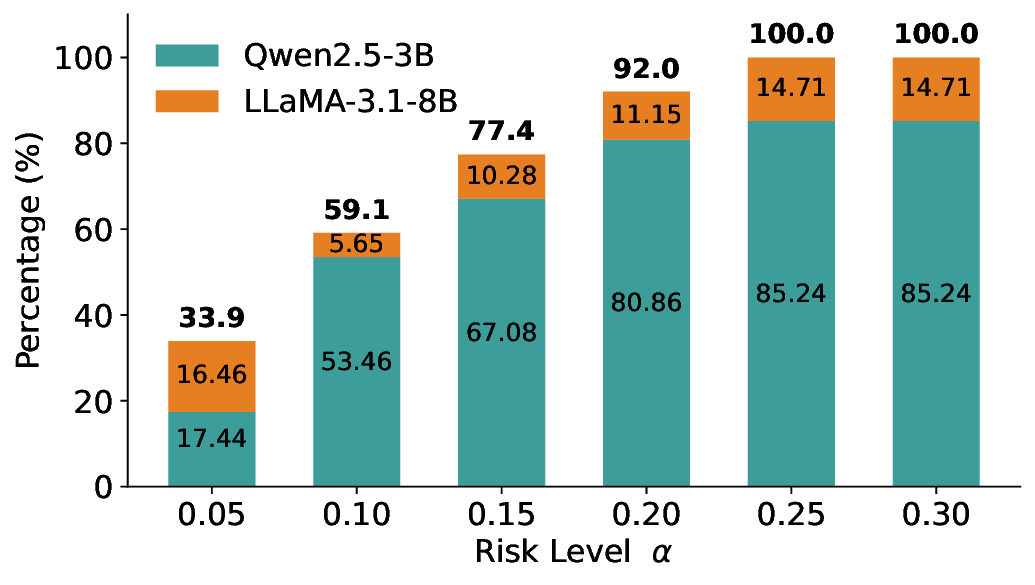
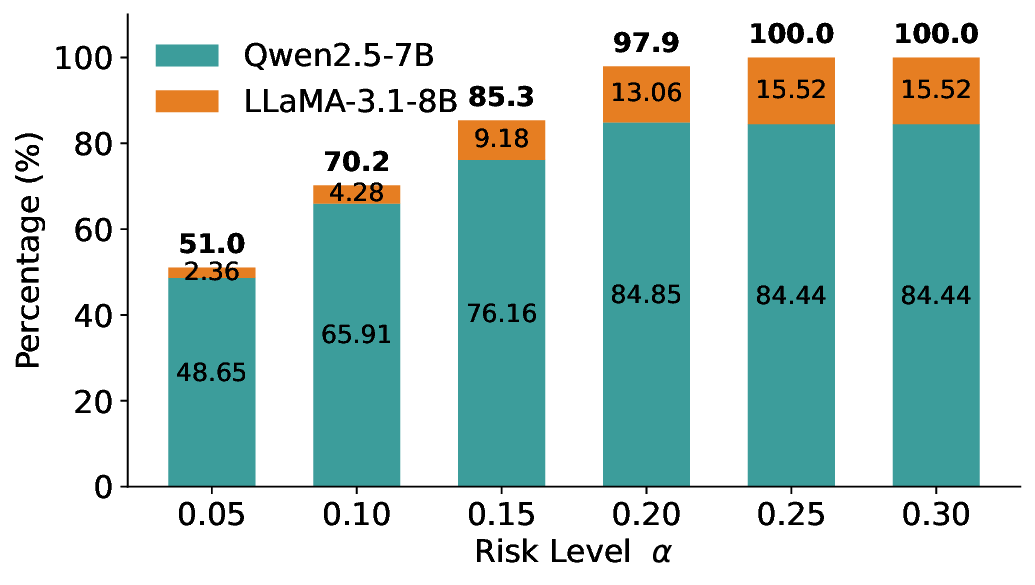
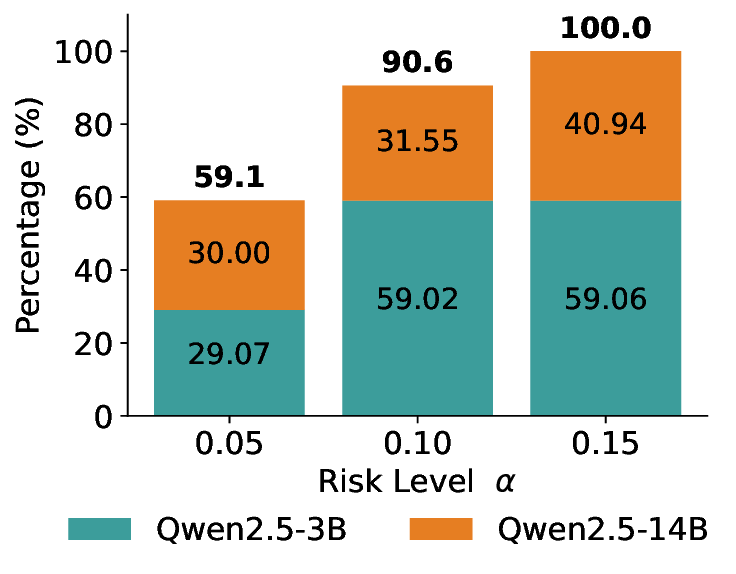
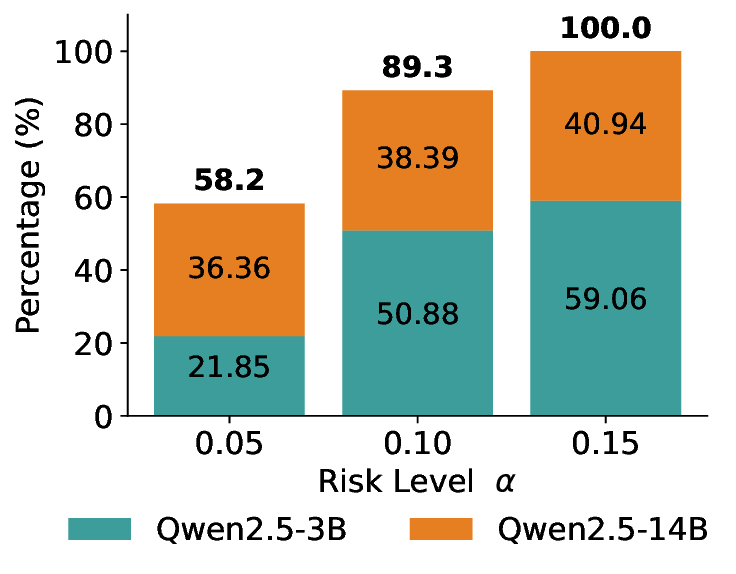
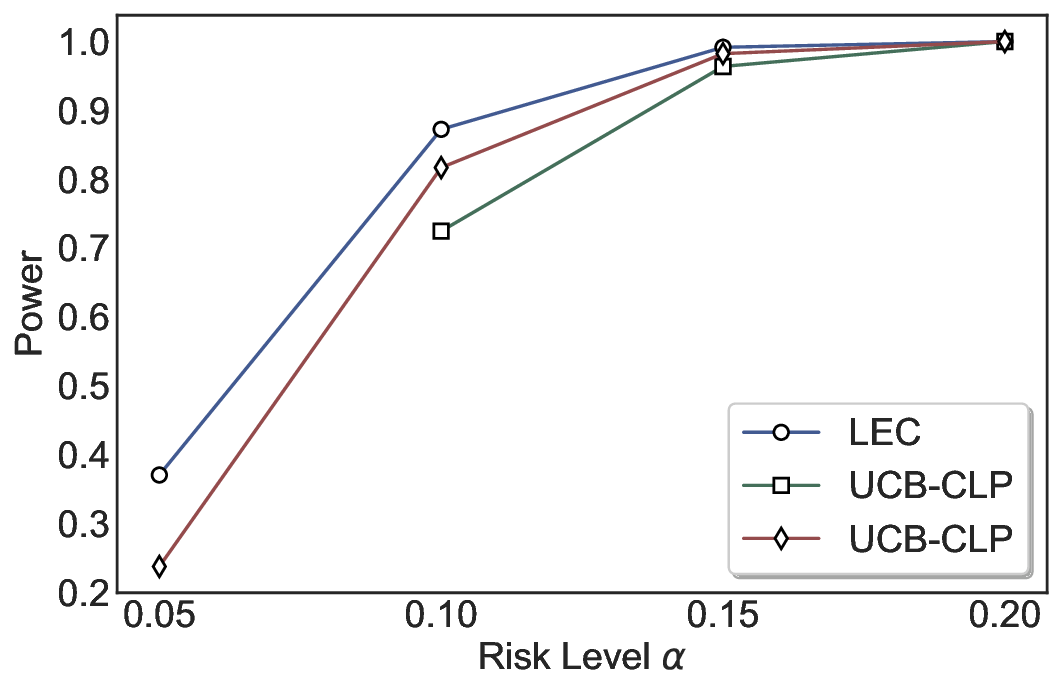
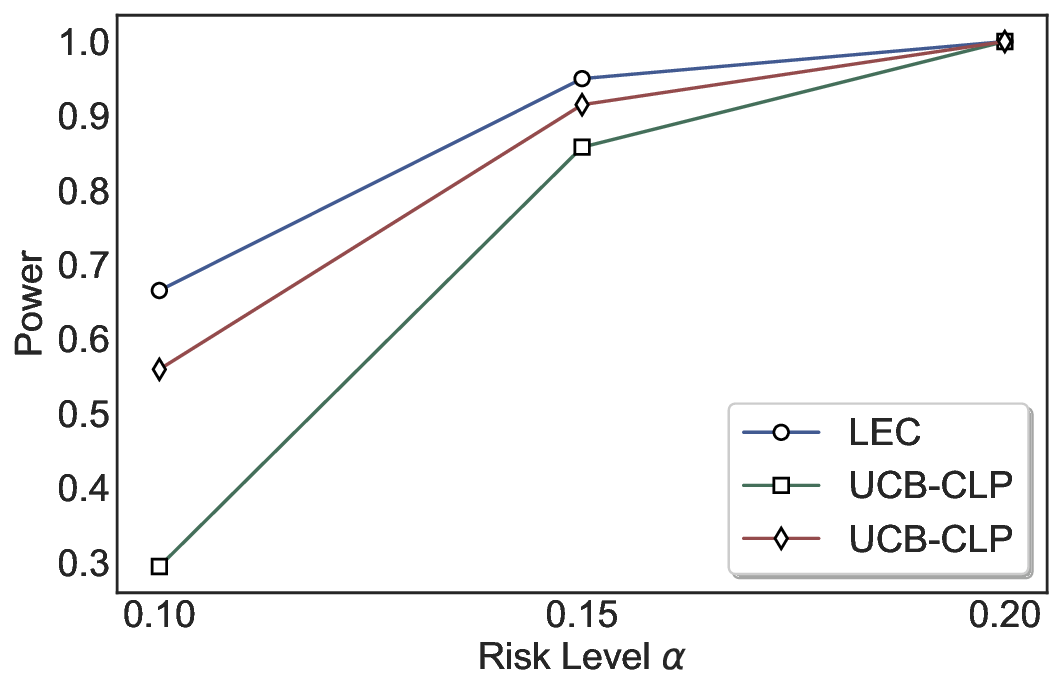
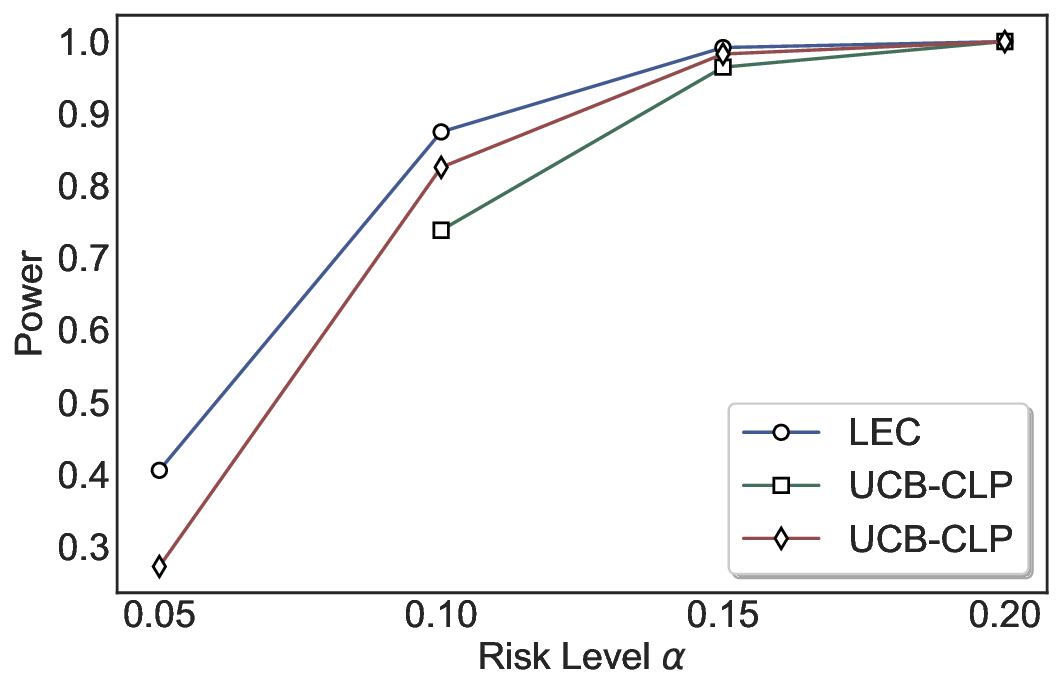
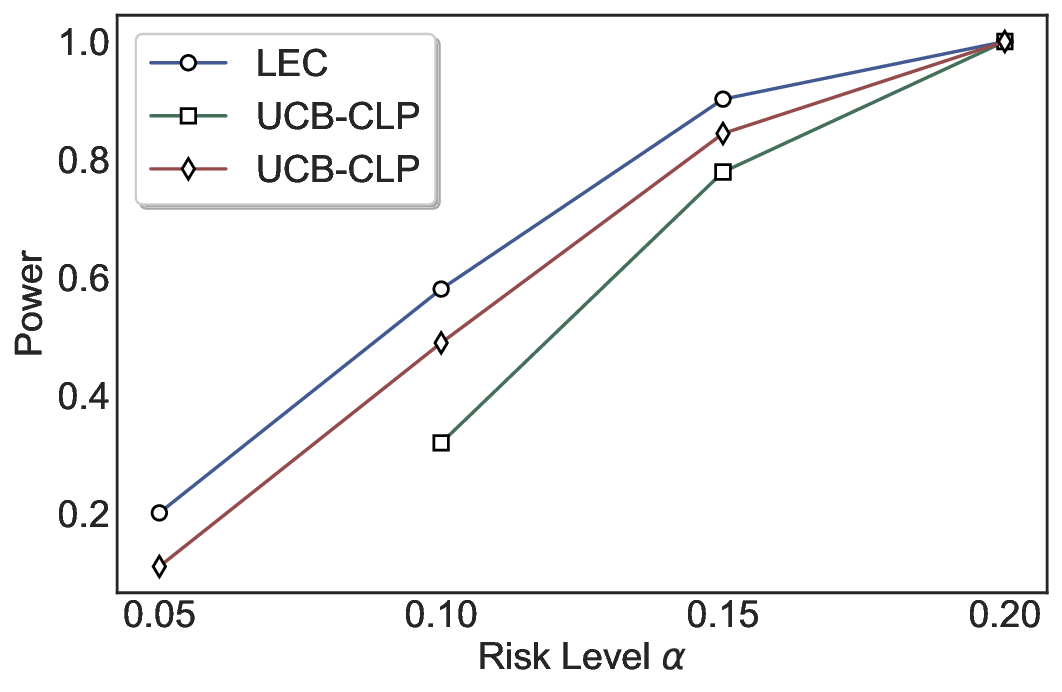
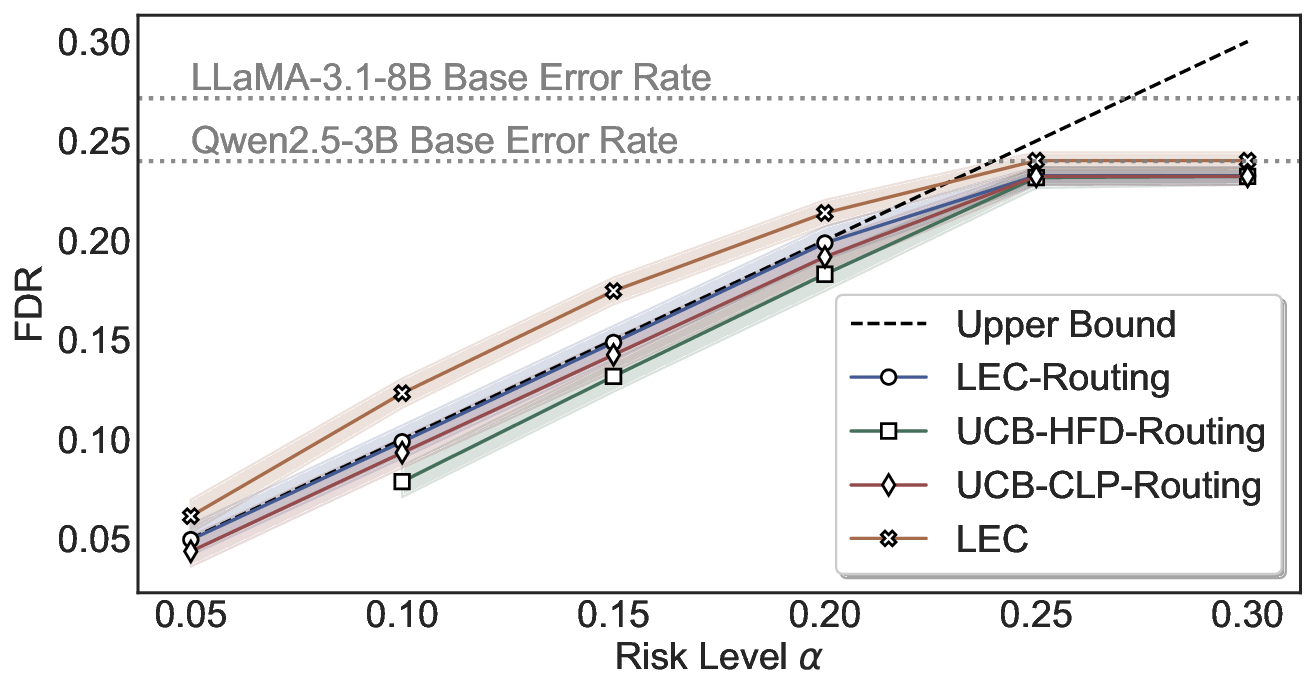
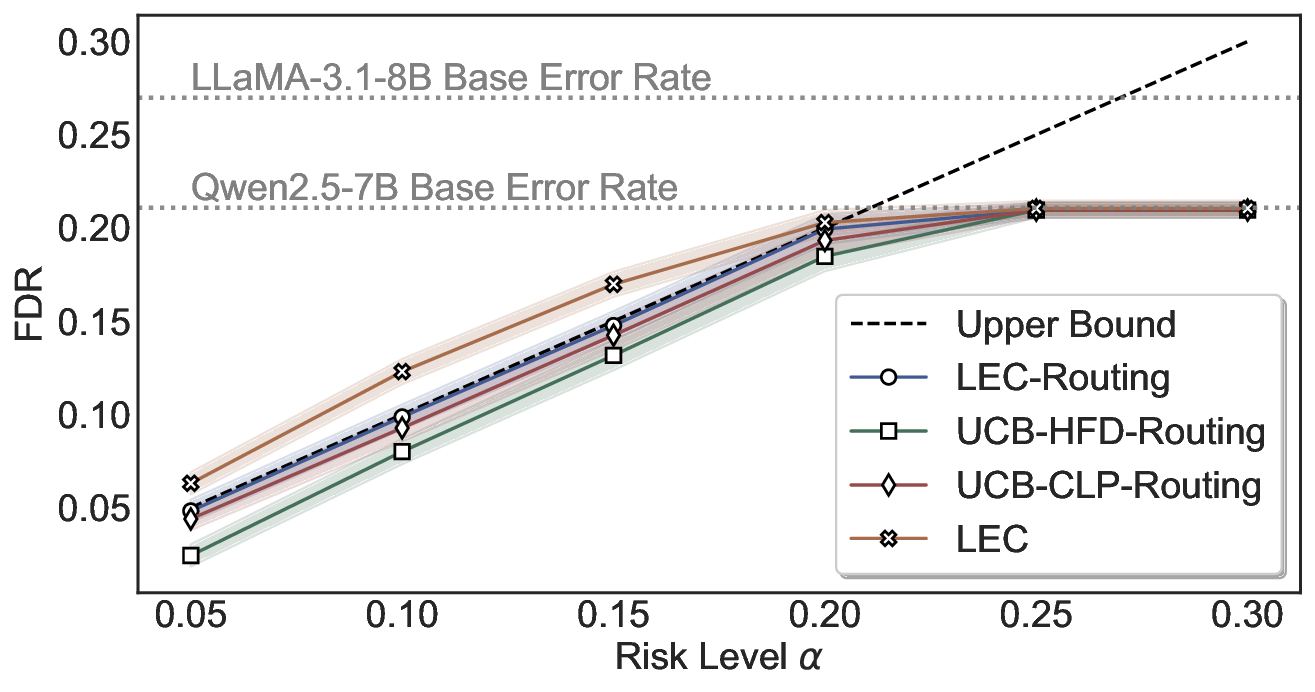
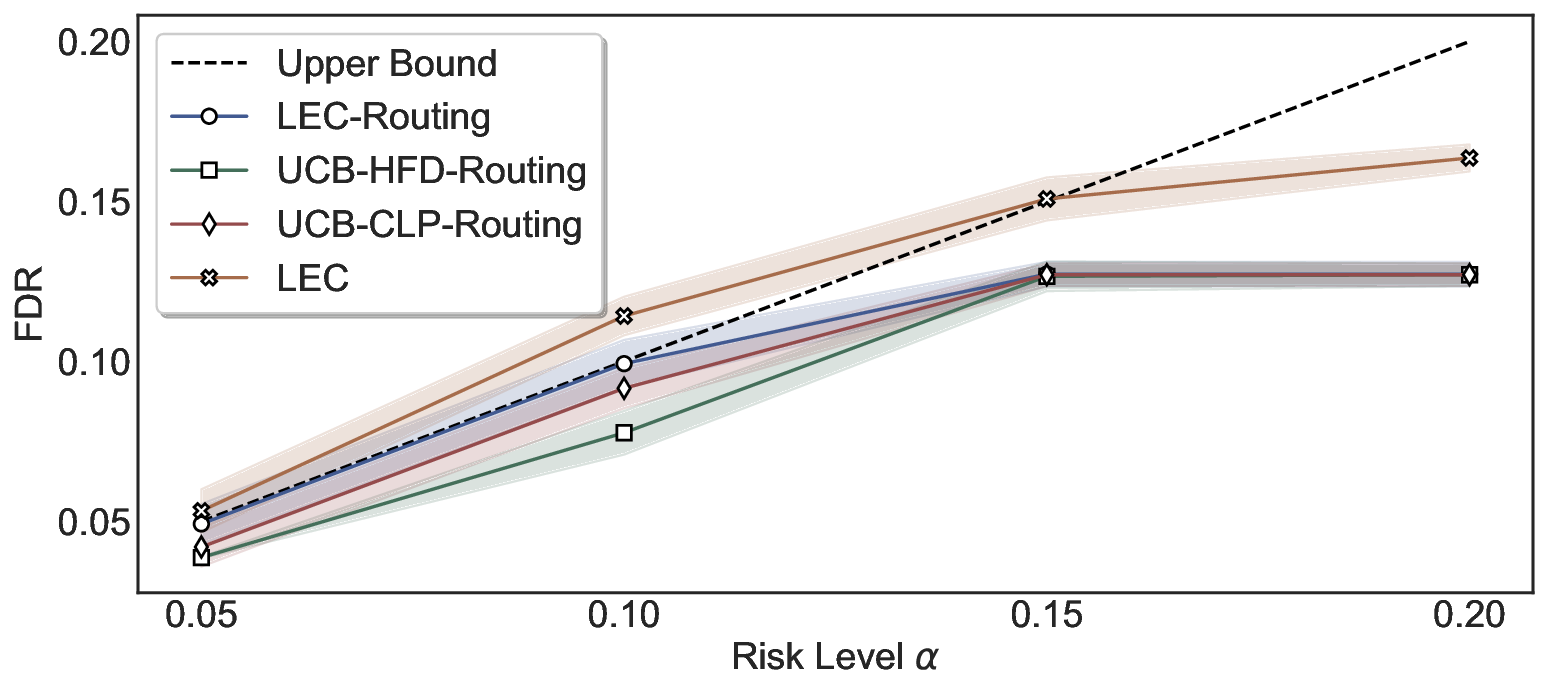
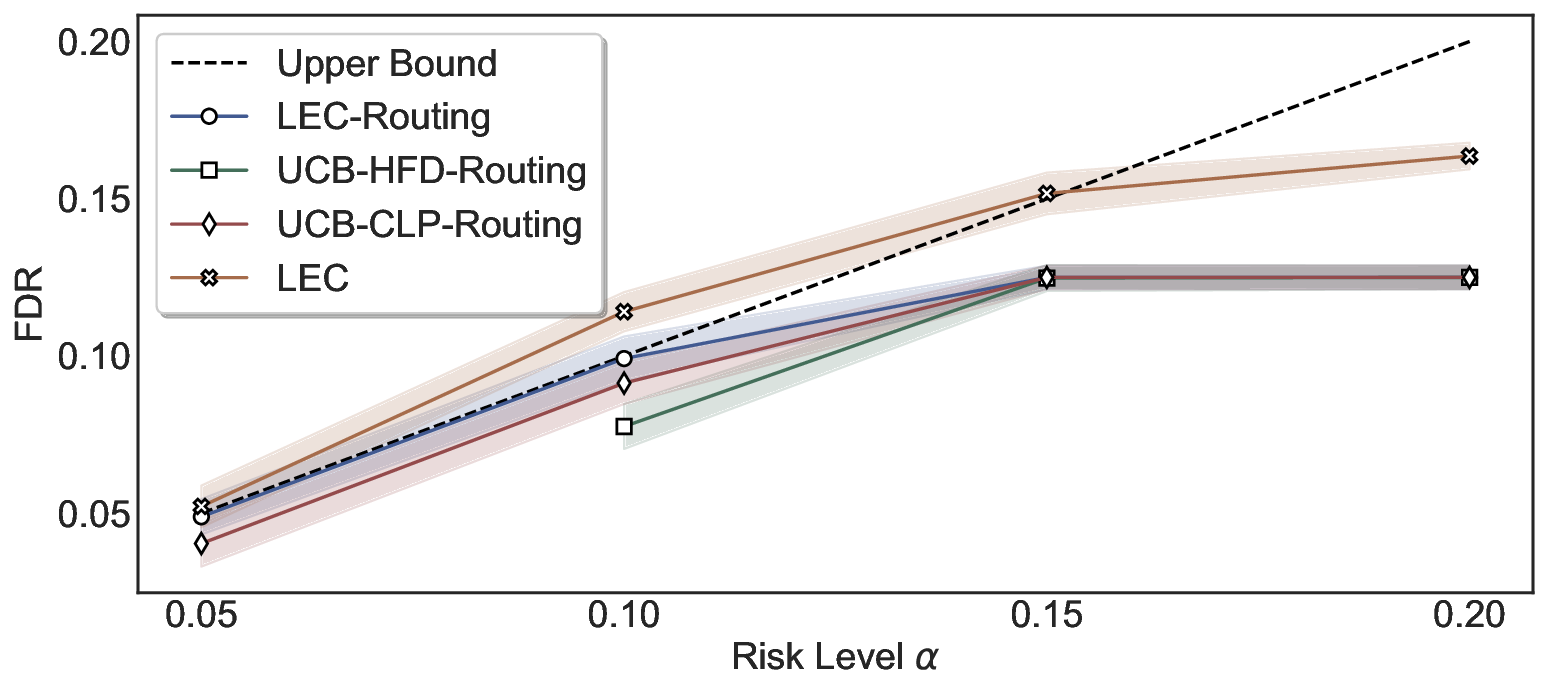
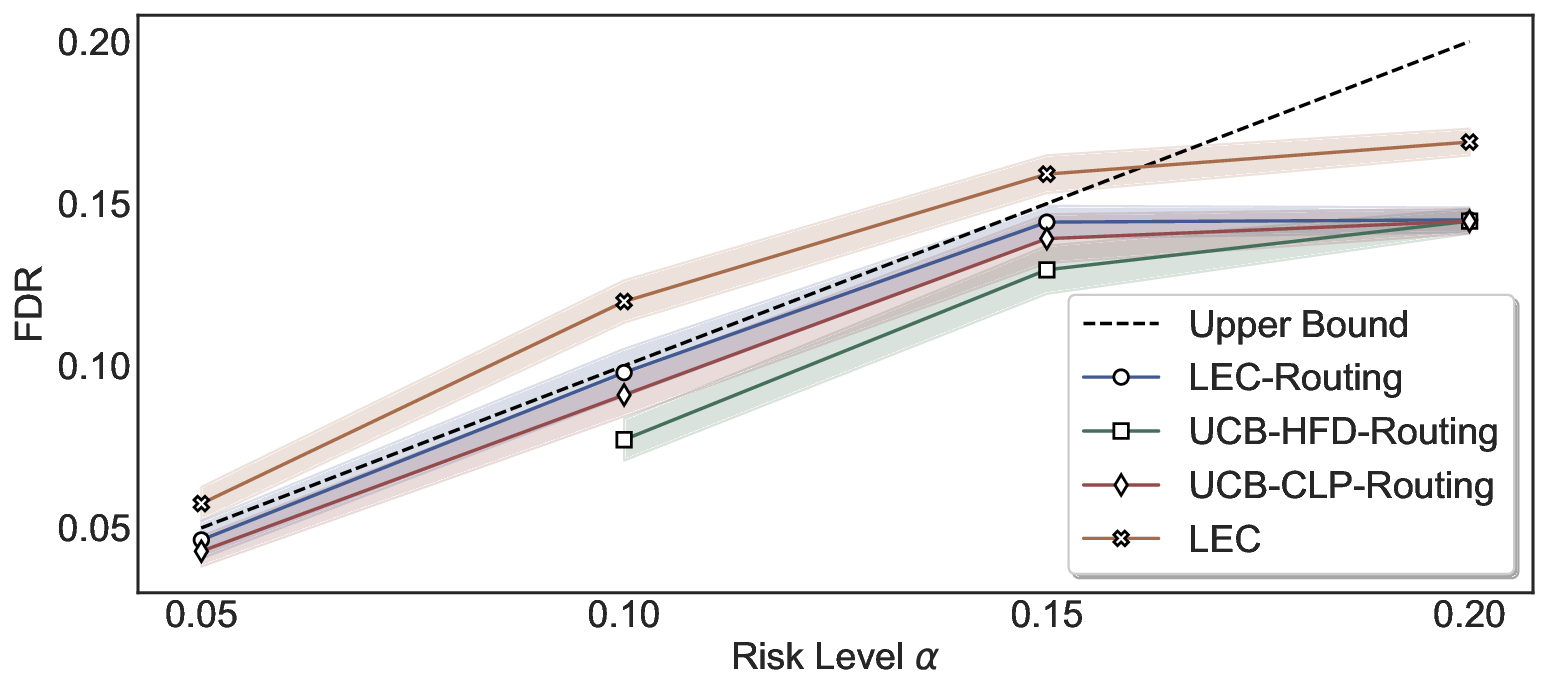
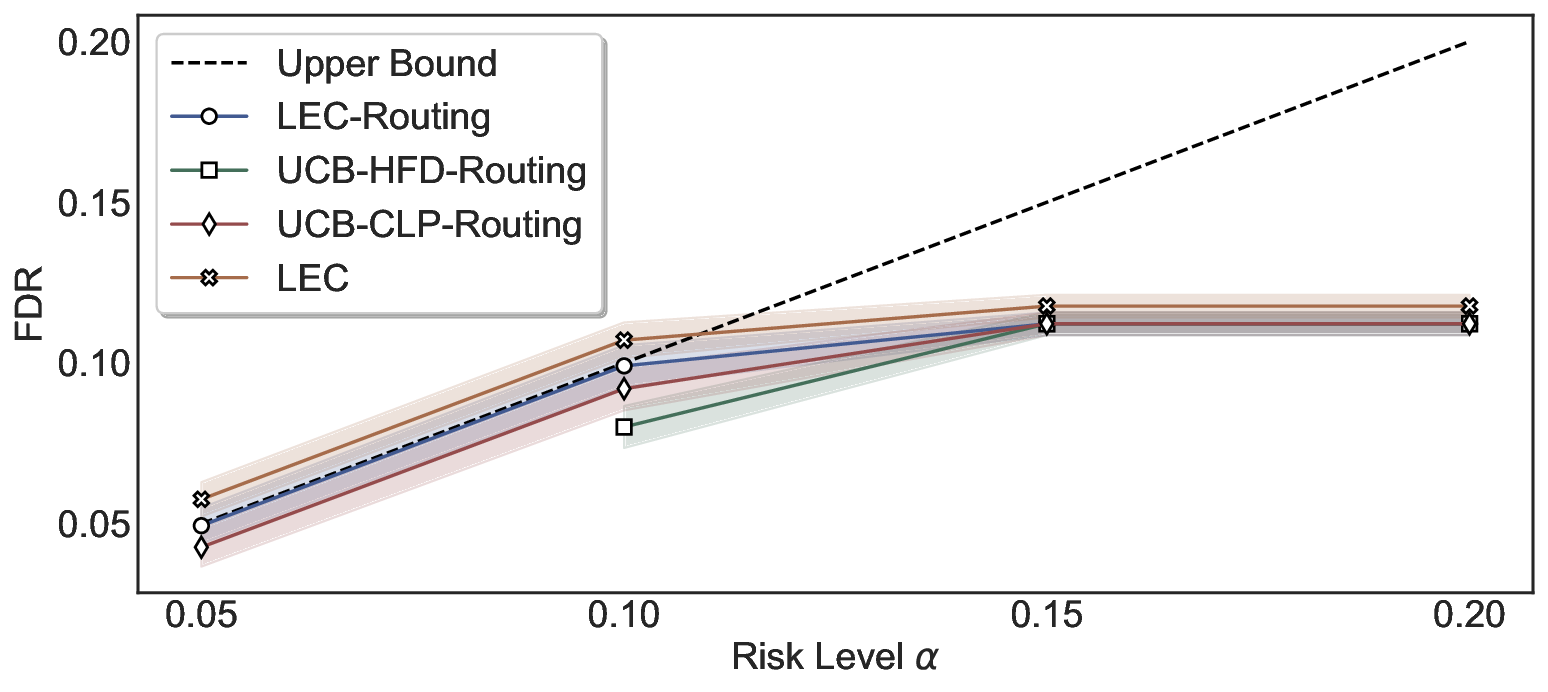
이 불등식을 만족하는 가장 큰 선택 비율을 찾는 과정은 단일 임계값을 조정하는 문제로 환원된다. 저자들은 이 임계값을 보정 데이터에 대해 순차적으로 탐색함으로써, 제한된 샘플 수에서도 정확한 FDR 보장을 제공한다는 점을 실험적으로 확인한다. 특히, “두 모델 라우팅” 확장은 실용적인 시스템 설계에 큰 의미를 가진다. 기본 모델이 높은 불확실성을 보이면, 보다 정교하거나 비용이 높은 보조 모델에게 입력을 넘겨주면서도 전체 시스템의 FDR을 동일하게 유지한다. 이는 비용‑효율적인 모델 배포와 신뢰성 확보를 동시에 달성할 수 있는 전략이다.
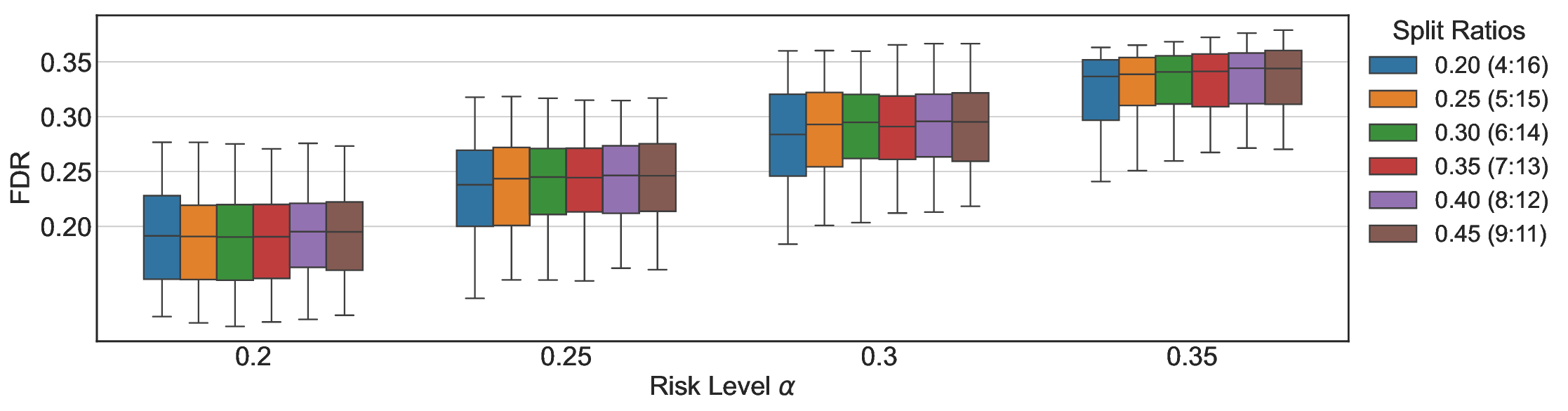
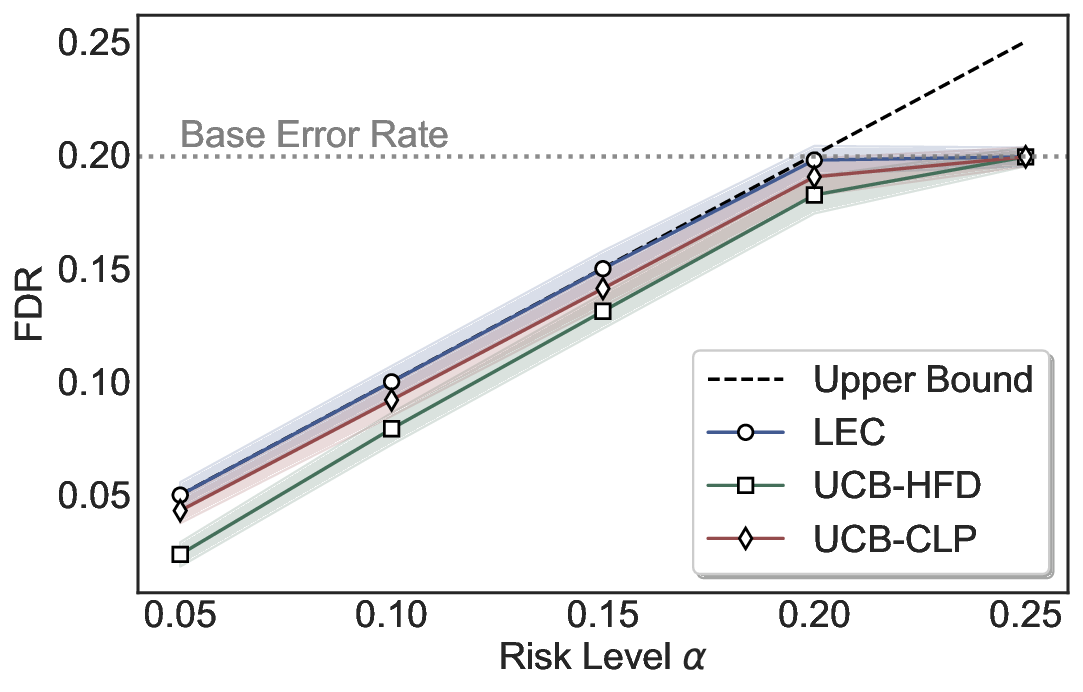
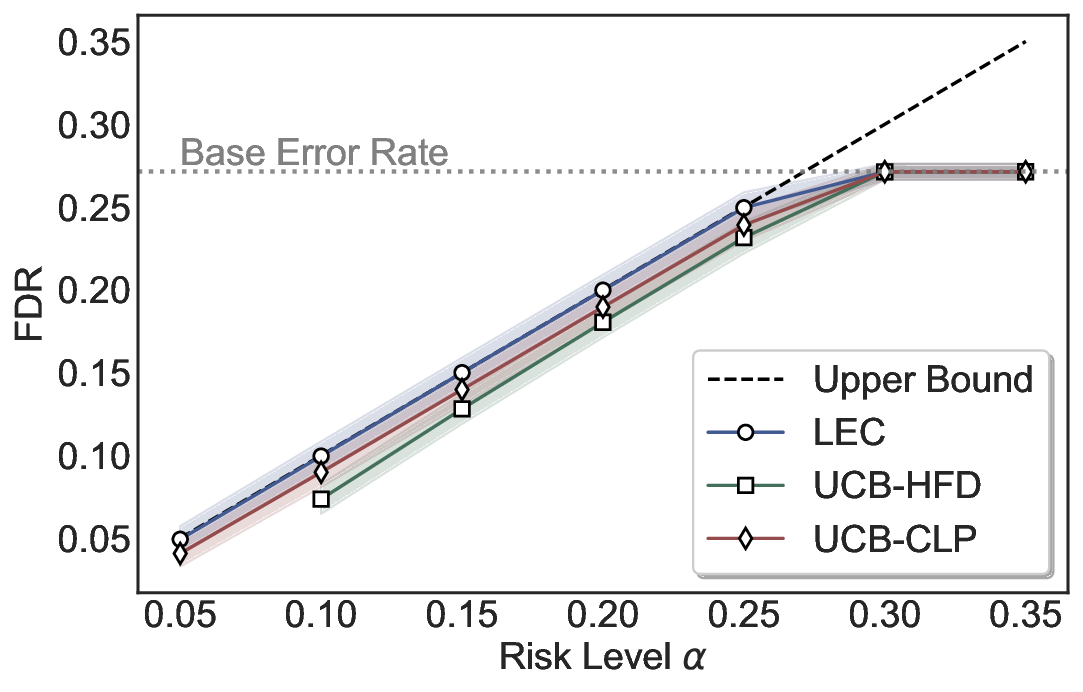
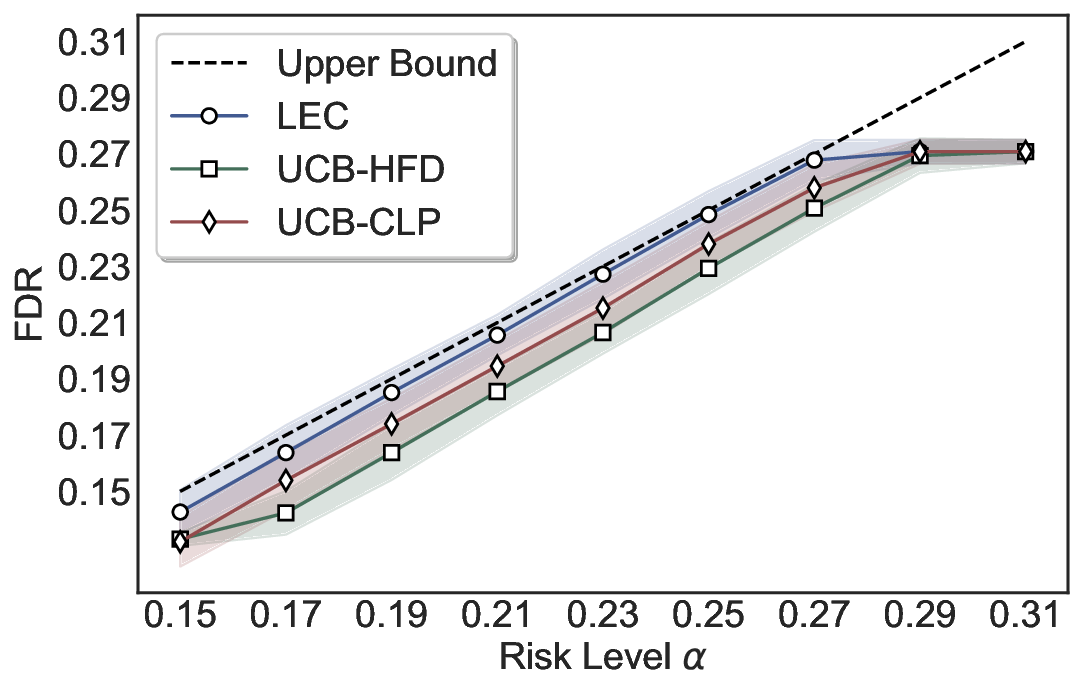
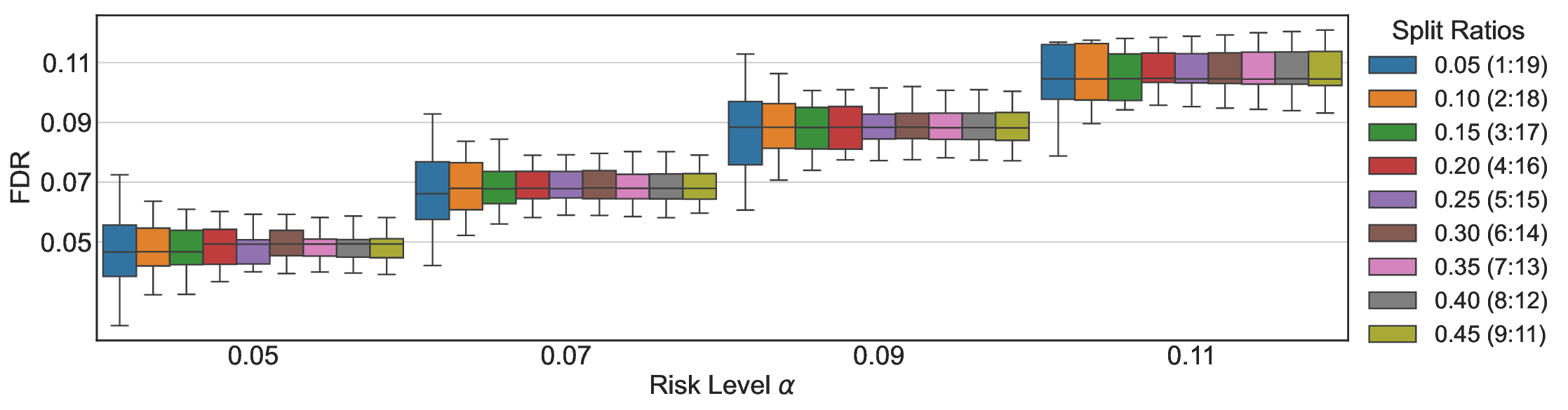
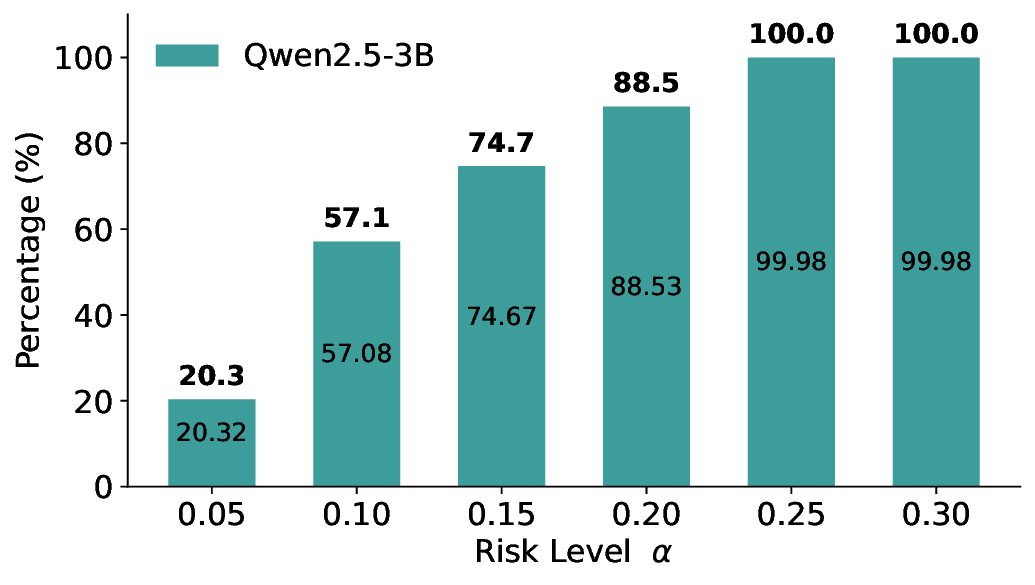
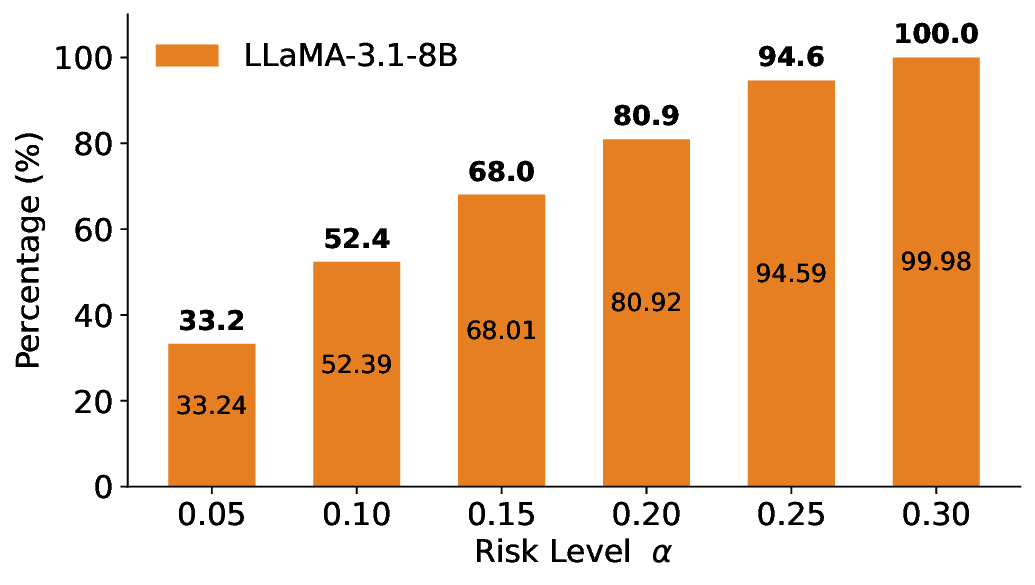
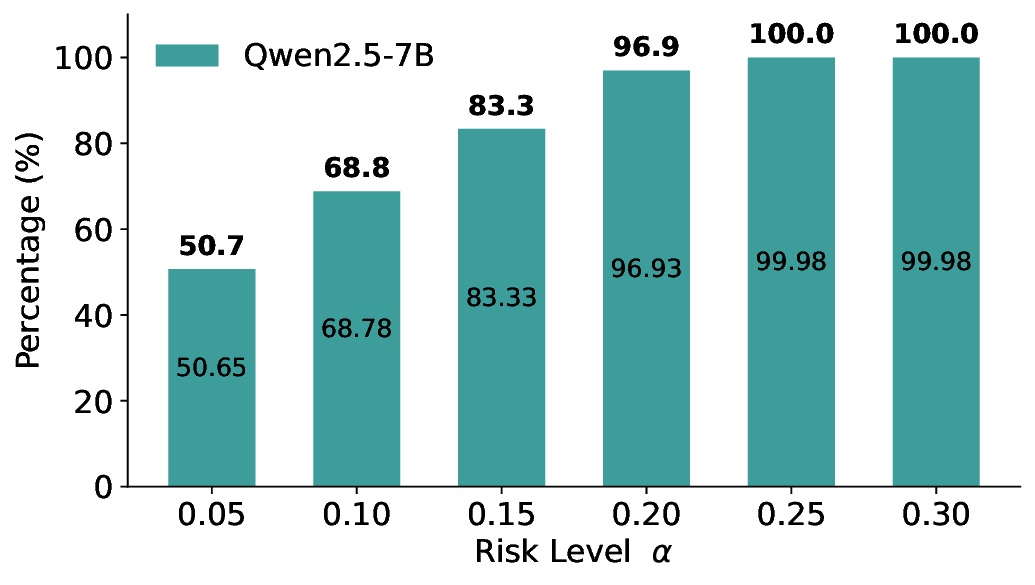
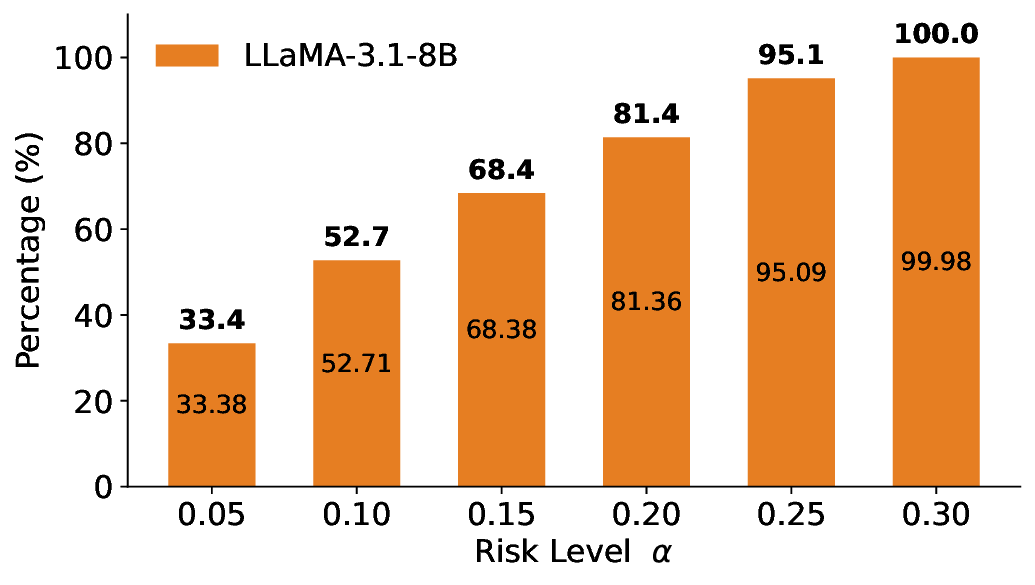
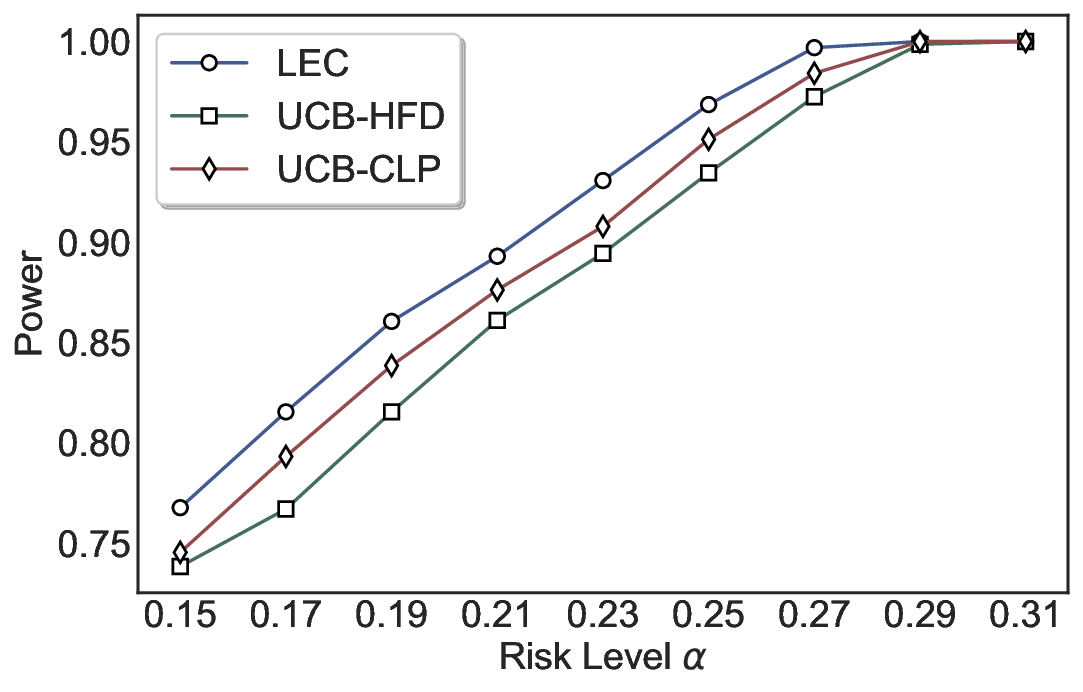
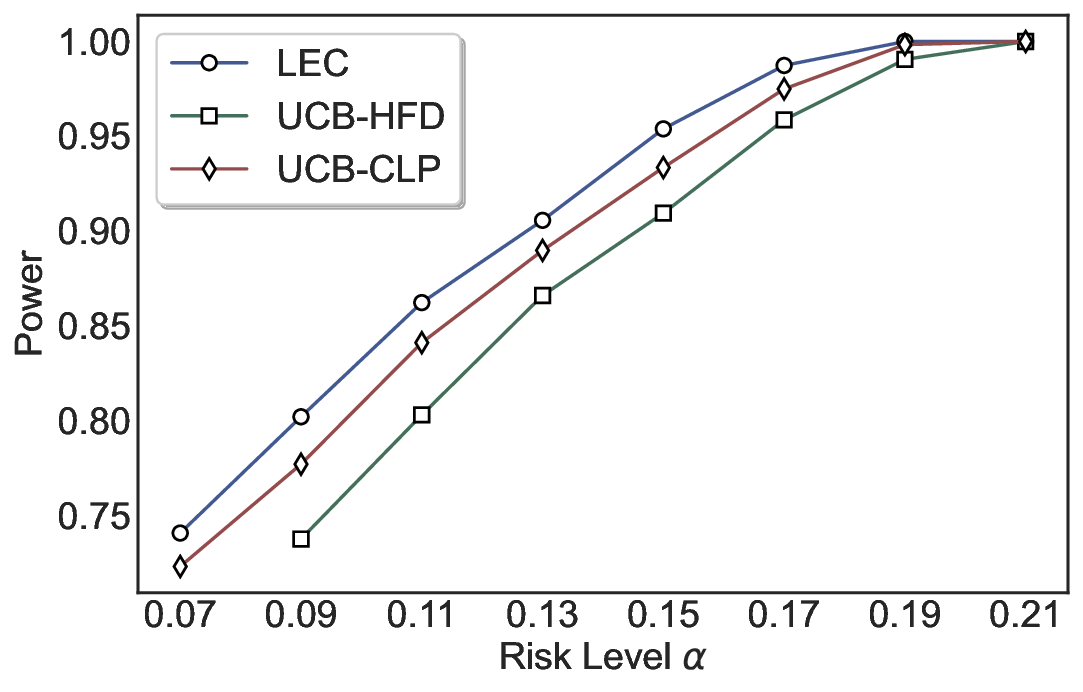
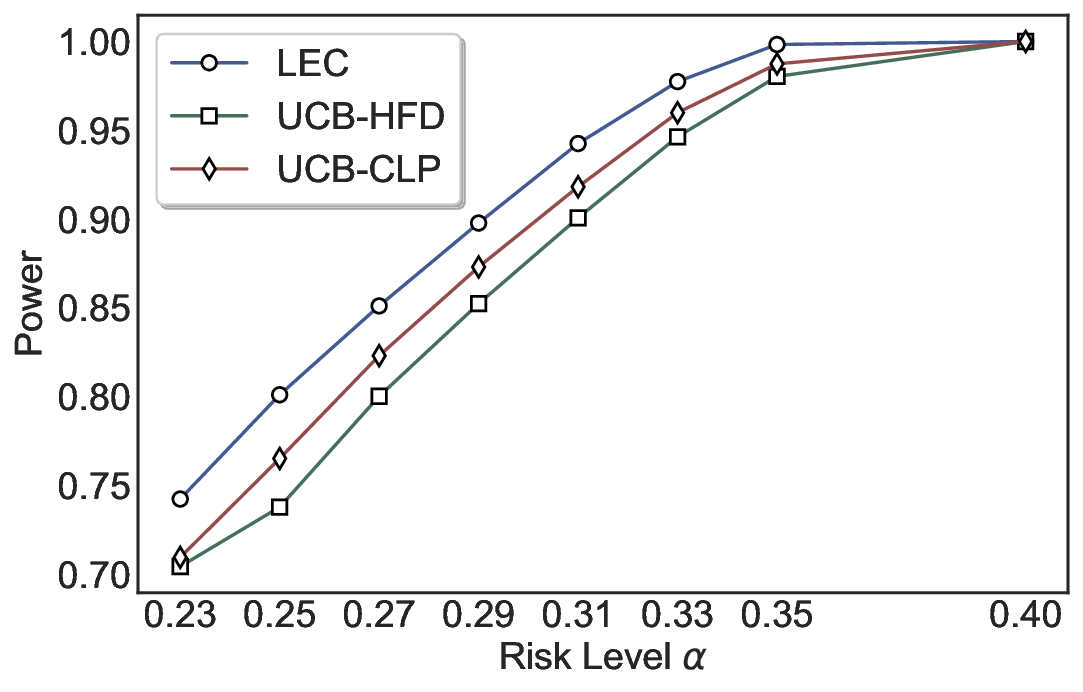
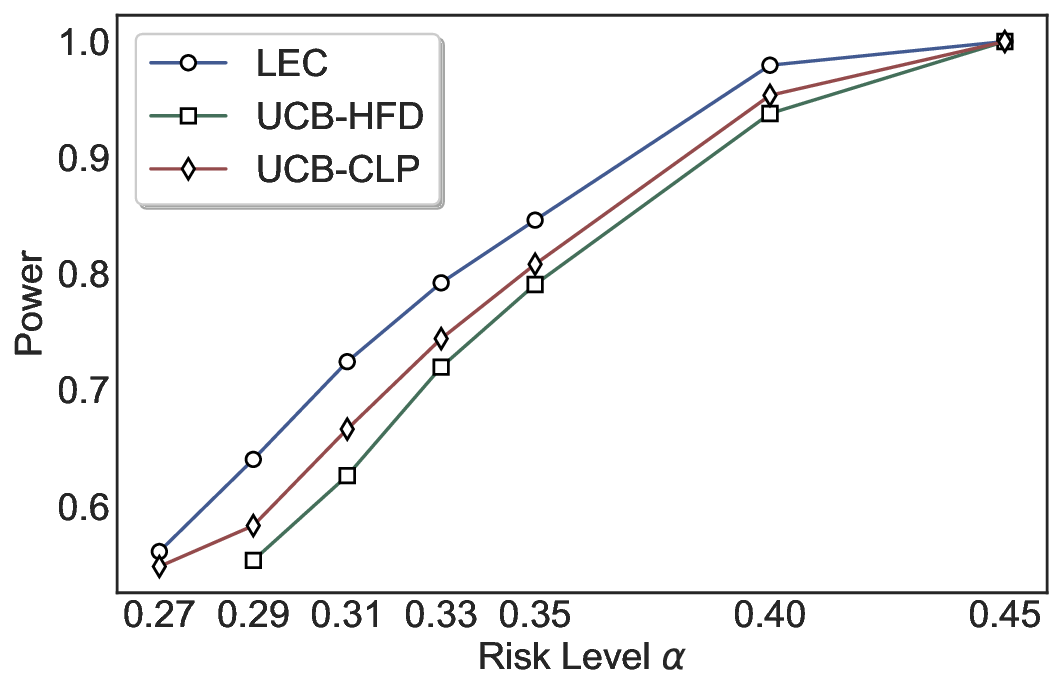
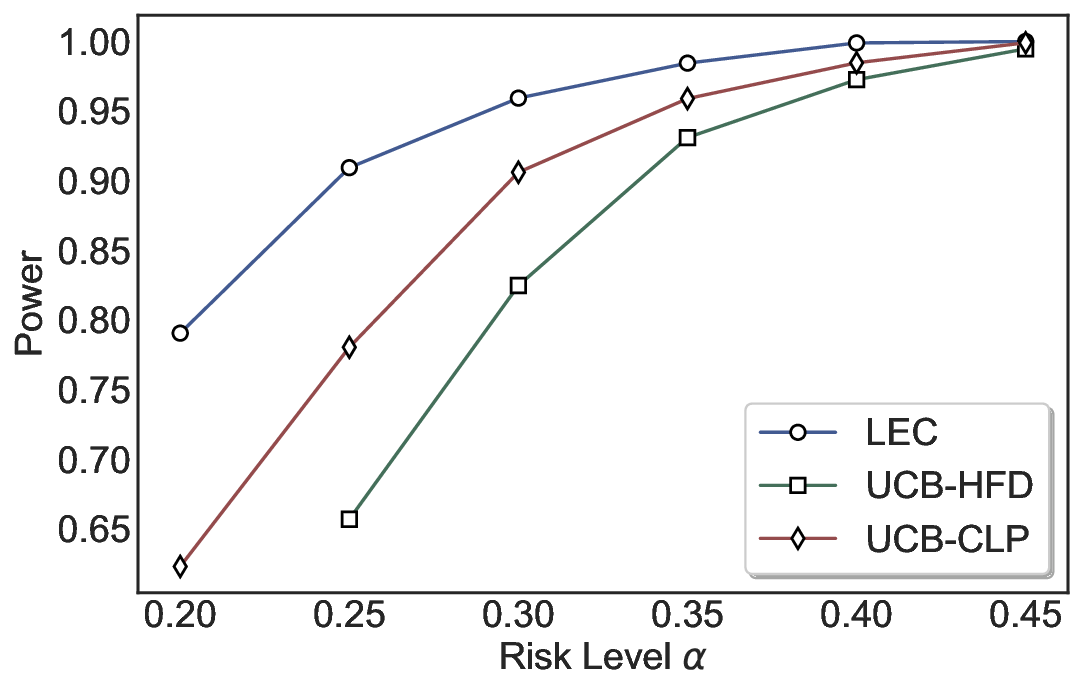
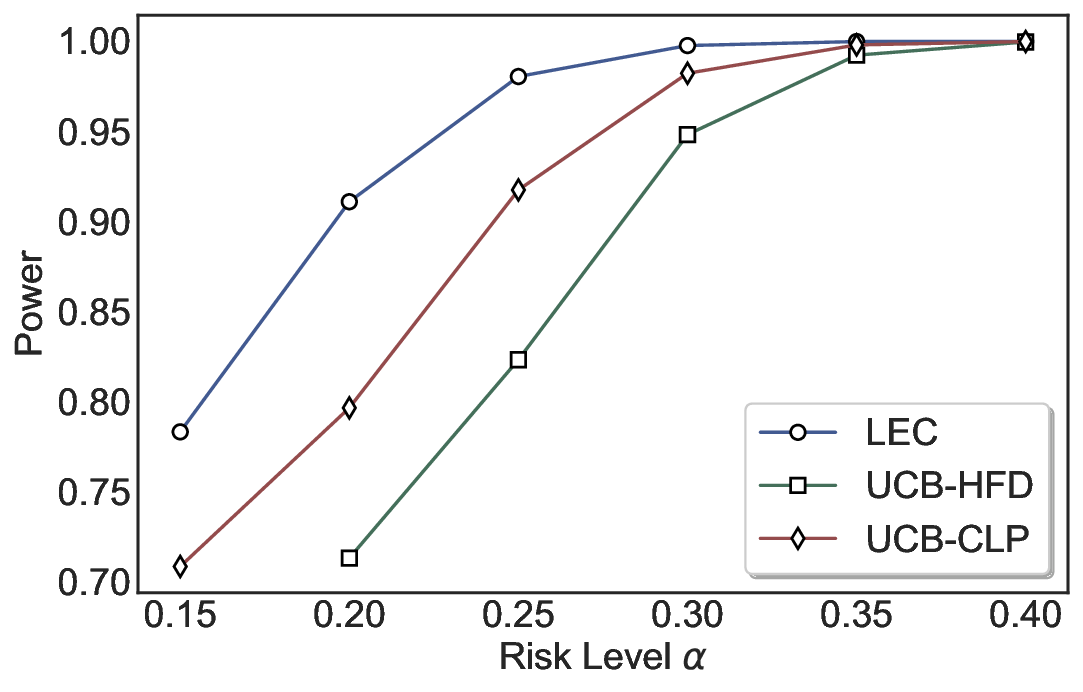
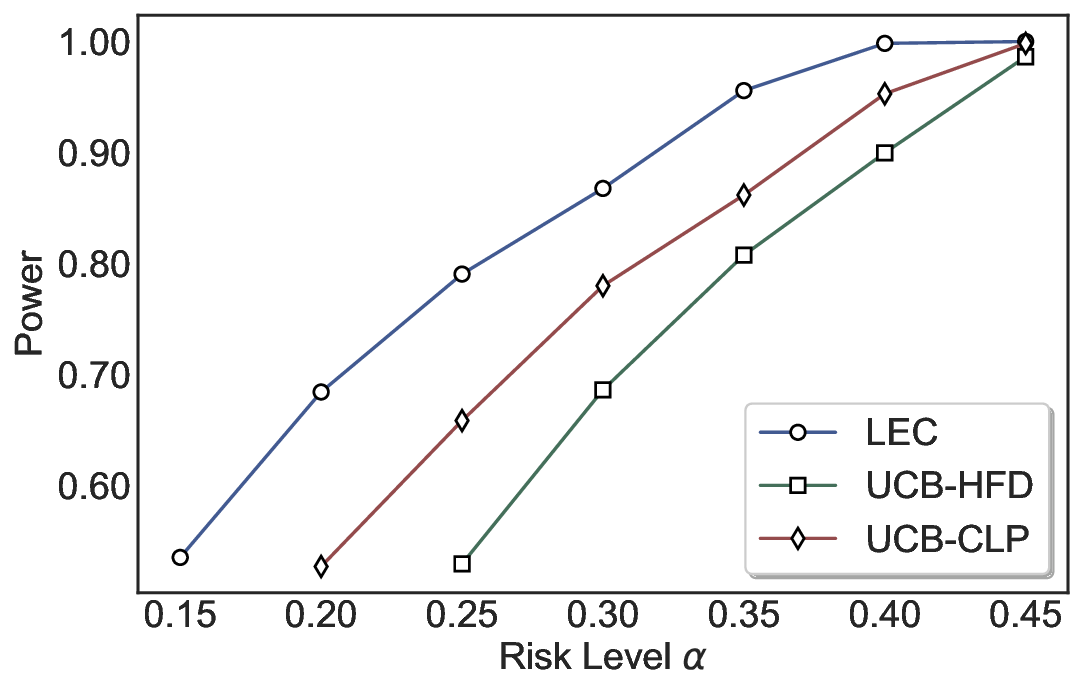
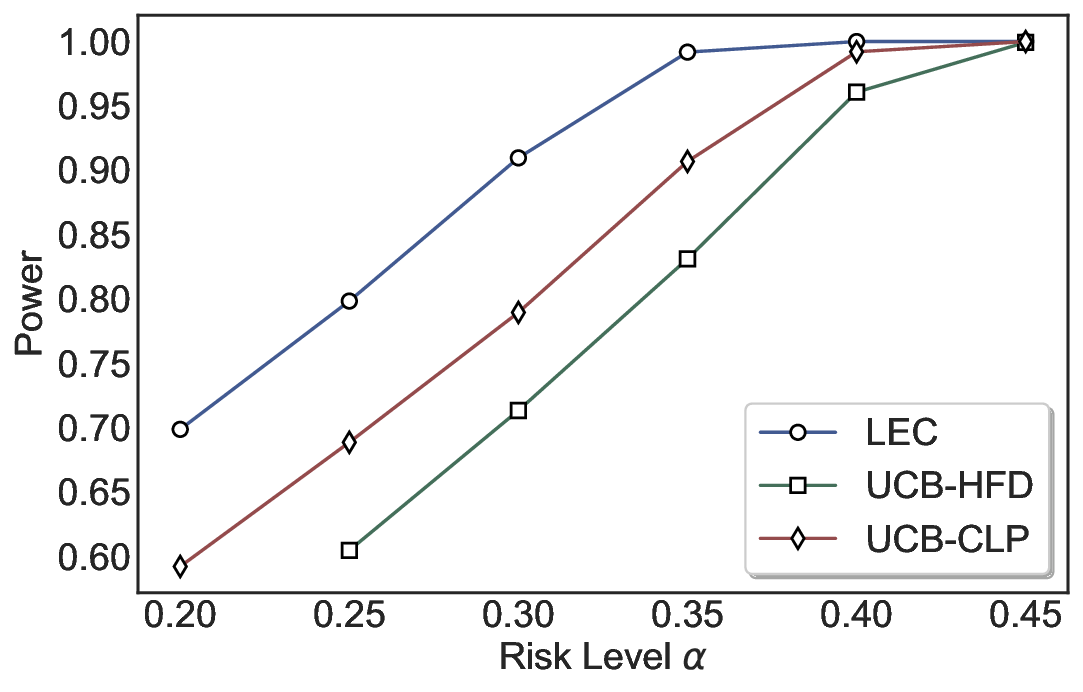
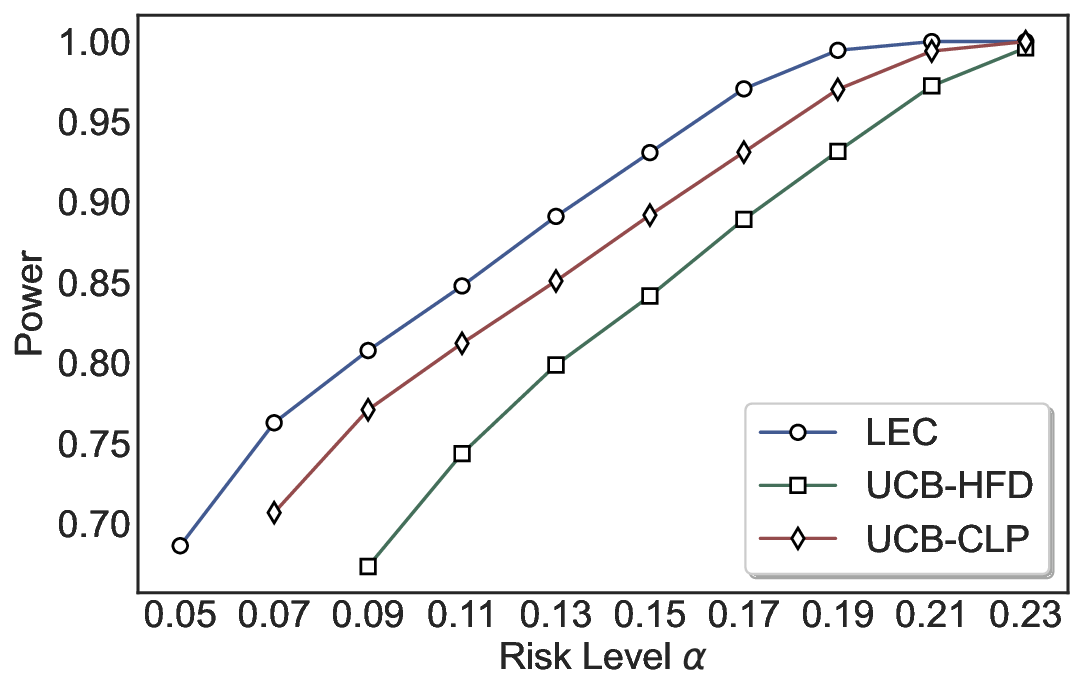
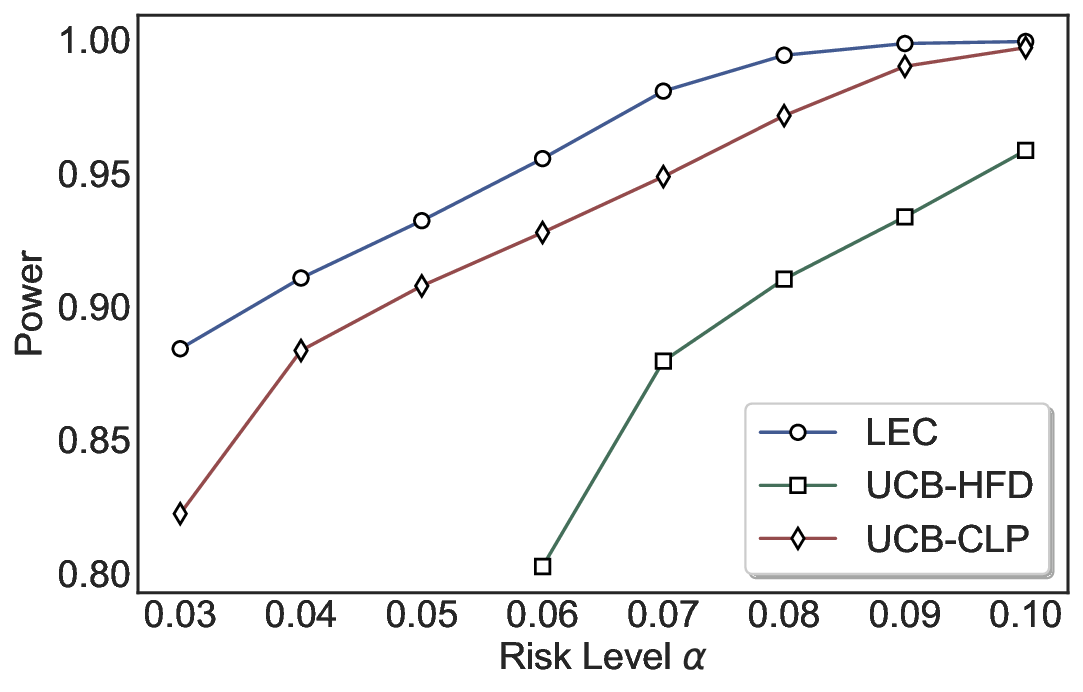
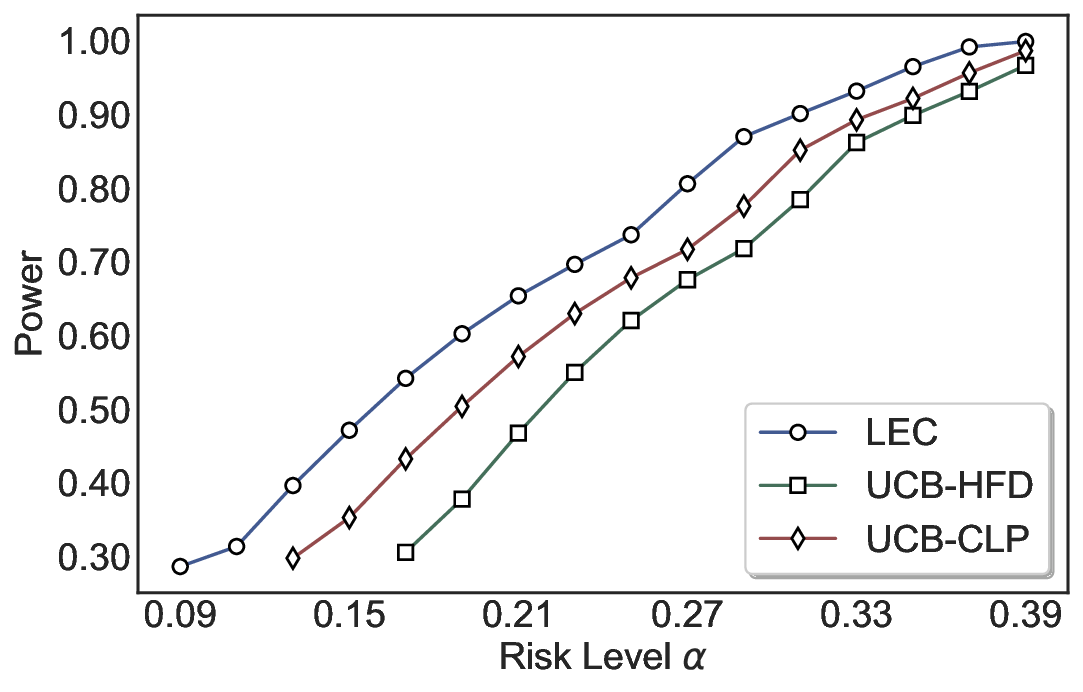
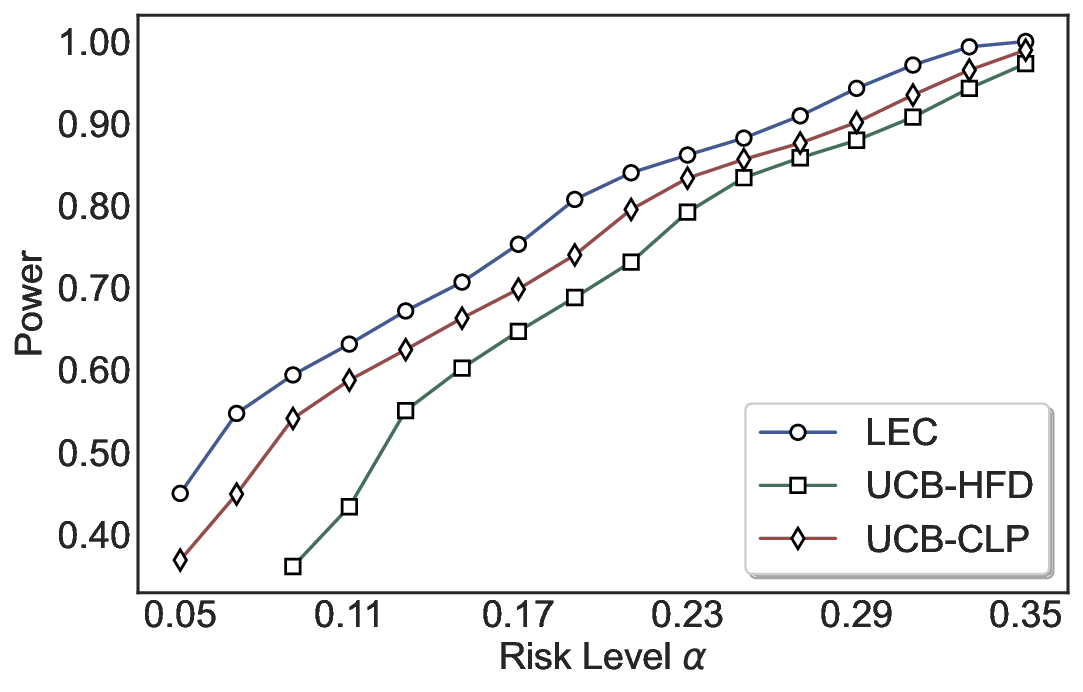
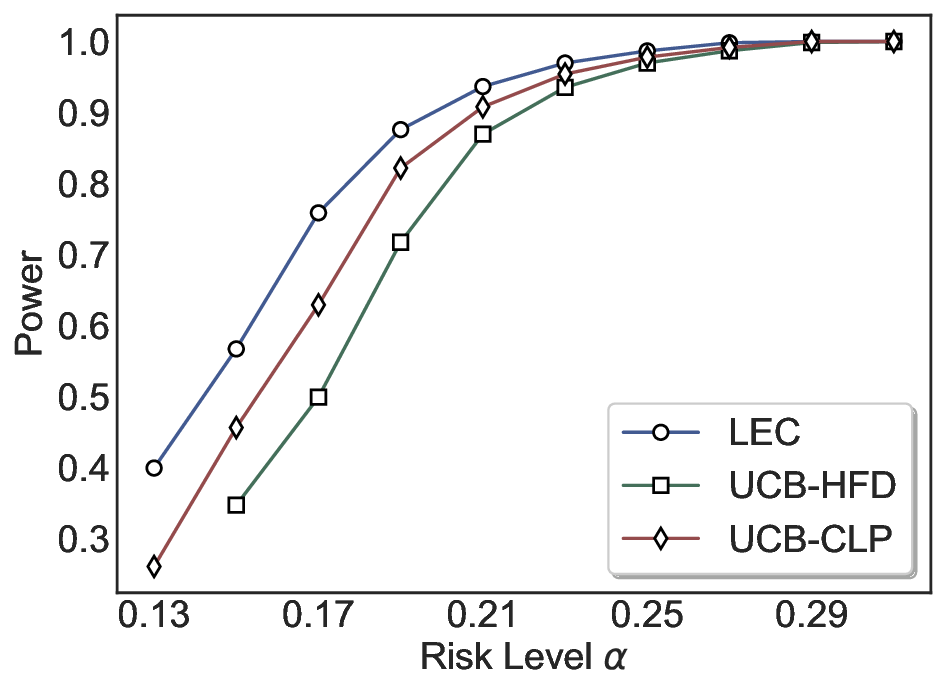
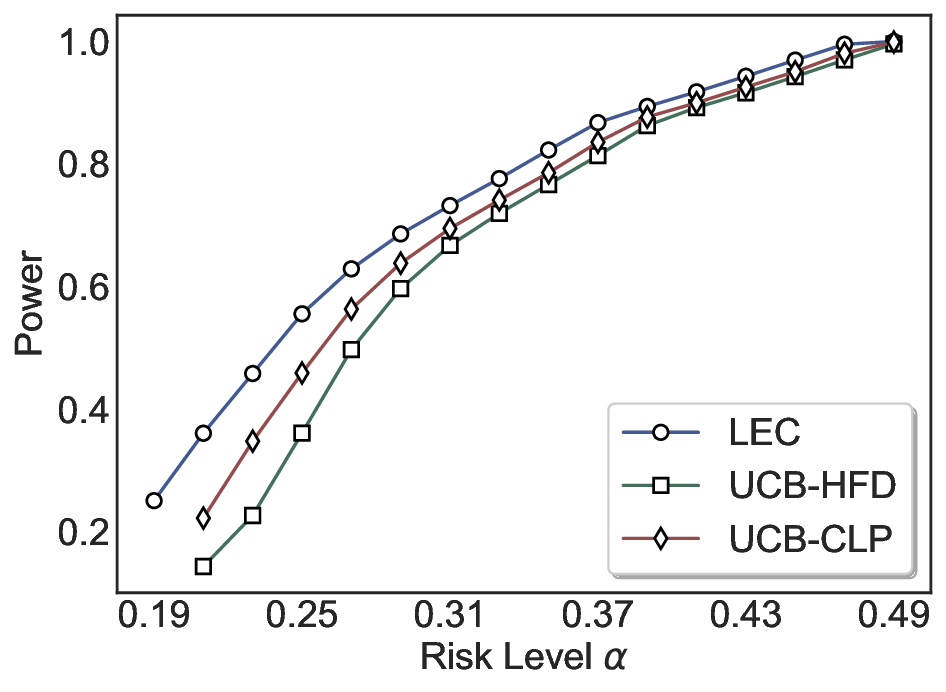
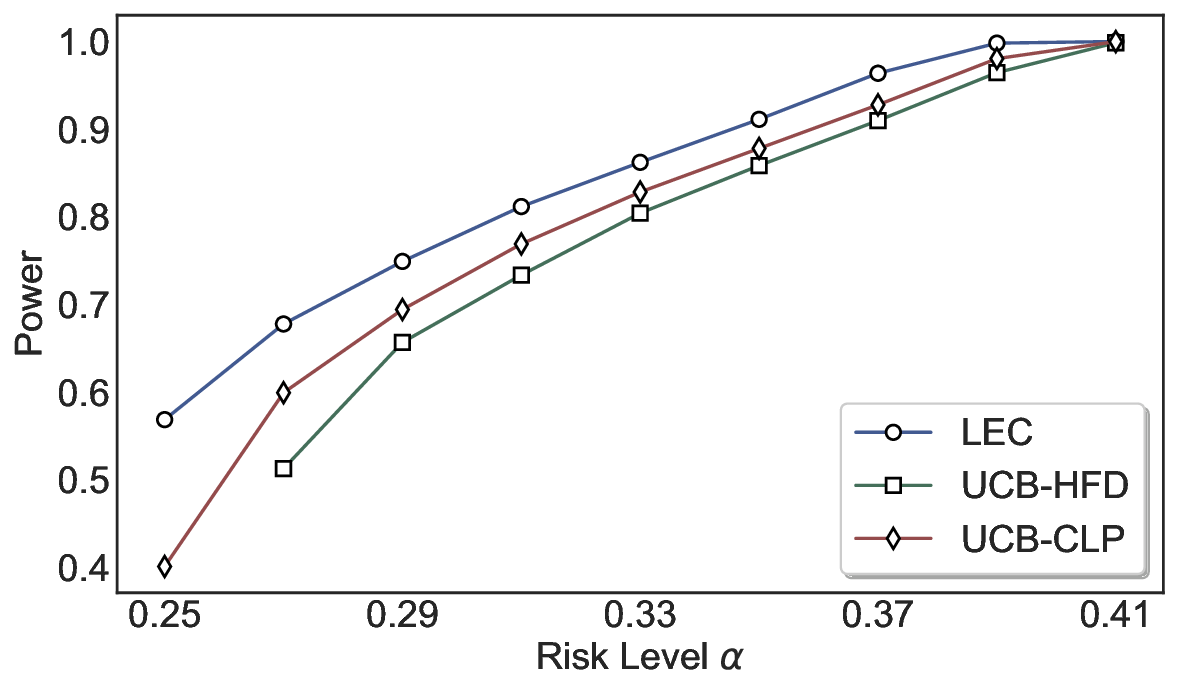
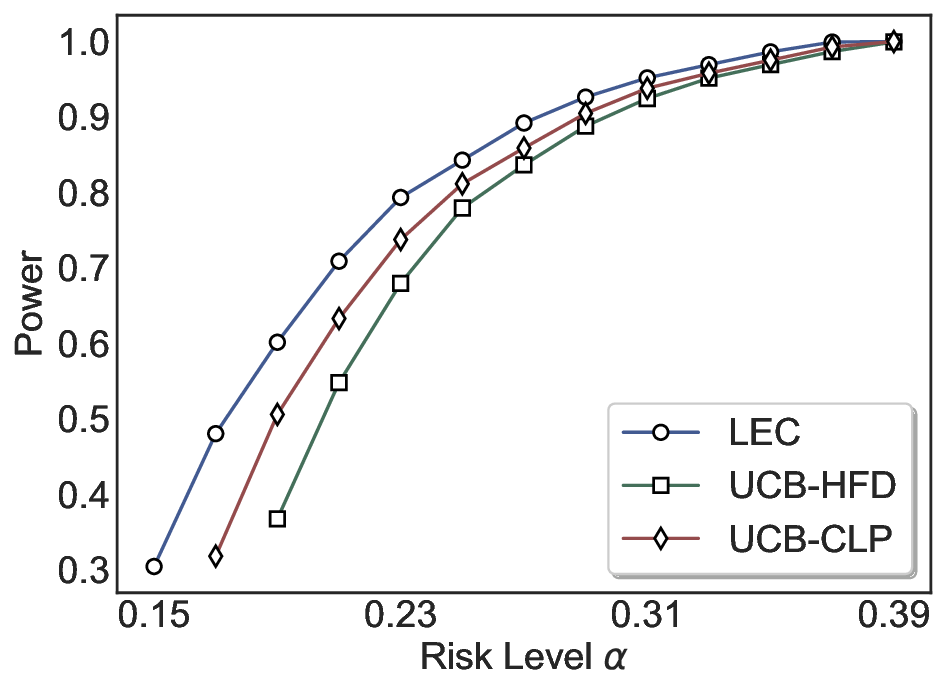
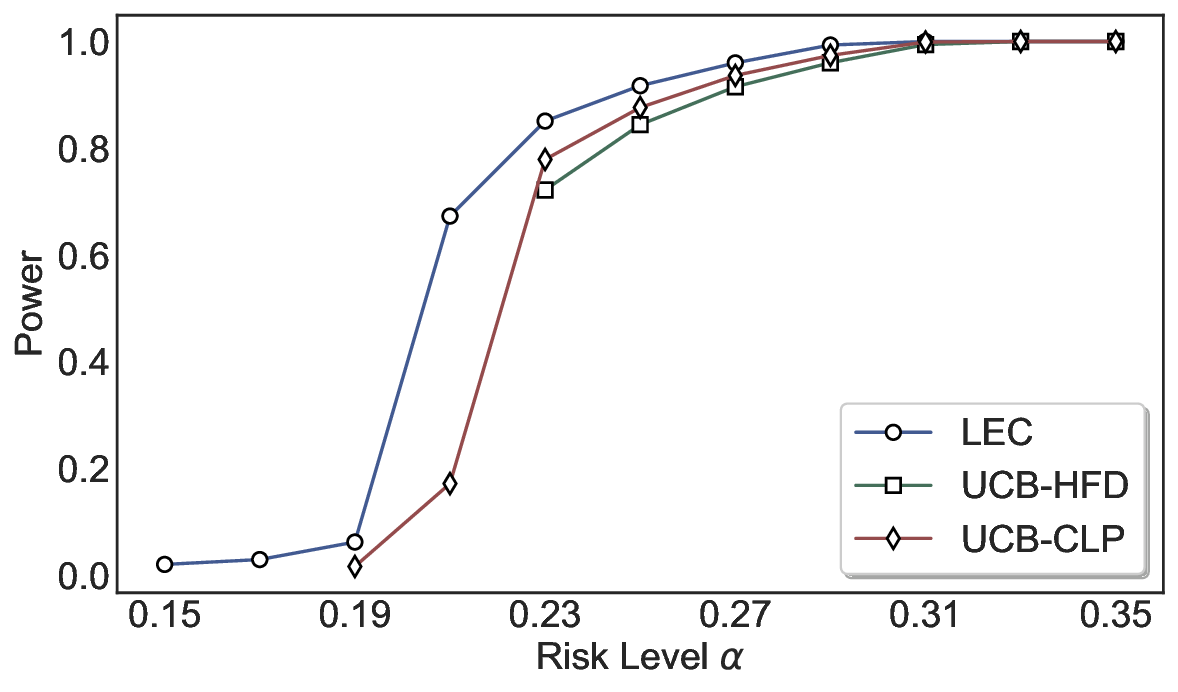
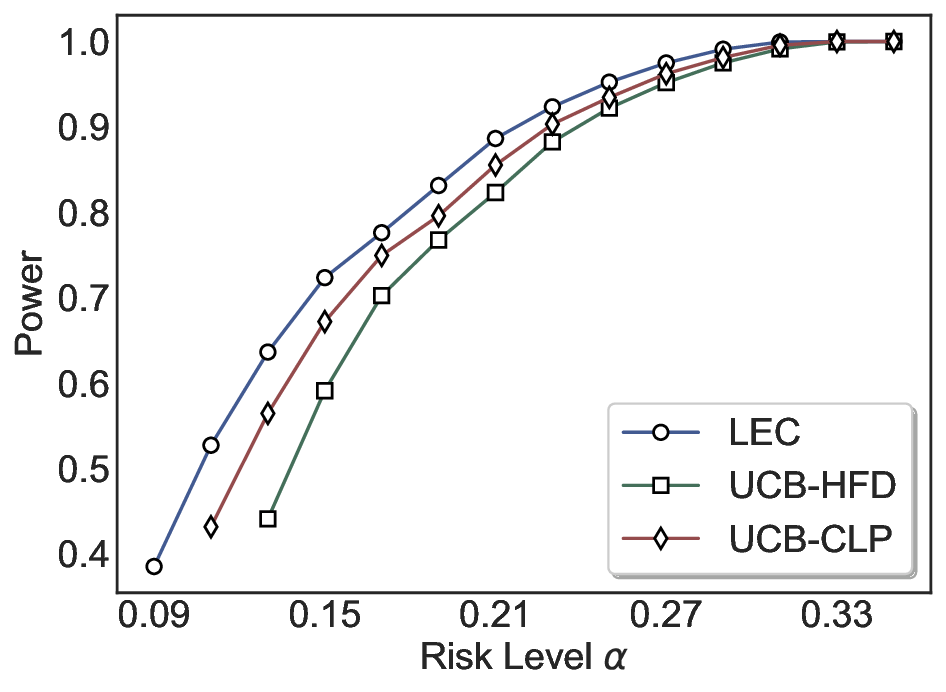
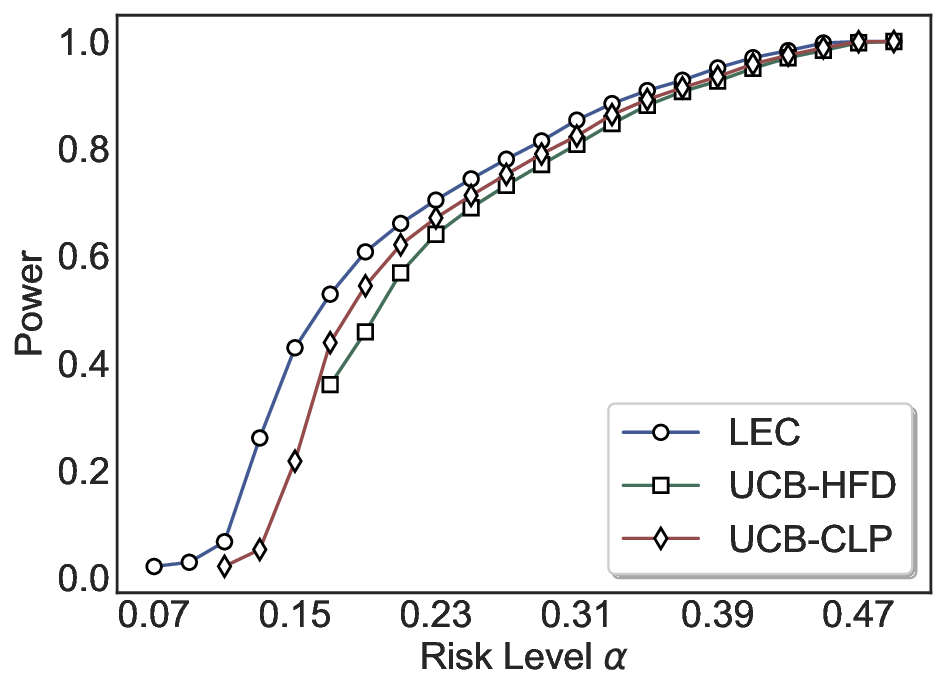
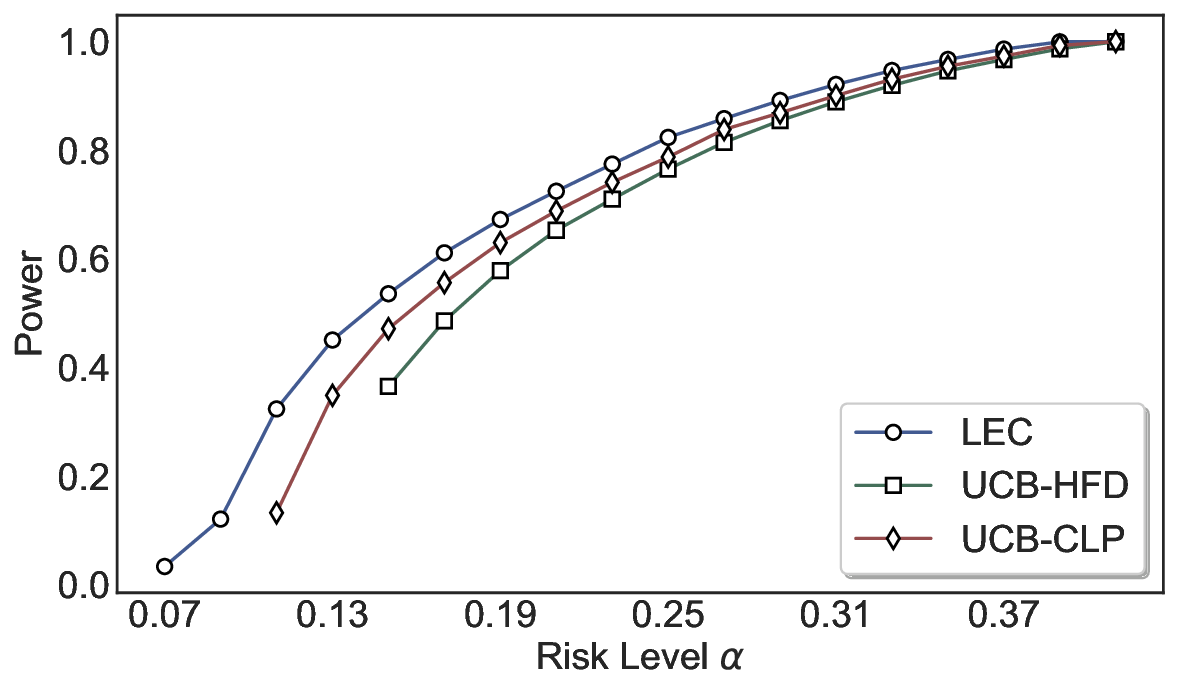
실험에서는 SQuAD, Natural Questions, VQA 등 다양한 폐쇄형·개방형 QA 데이터셋을 활용하였다. 기존 방법(예: Threshold‑Based, Conformal Prediction 등)과 비교했을 때, LEC는 목표 FDR을 초과하지 않음은 물론, 보존율(retention) 측면에서 평균 10‑20% 이상의 개선을 보였다. 특히, 개방형 질문처럼 답변이 다중형일 때도 안정적인 FDR 제어가 가능함을 입증하였다.
한계점으로는 보정 데이터가 원본 데이터와 완전히 교환 가능(exchangeable)해야 한다는 가정과, 선형 기대 제약이 복잡한 의존 구조를 충분히 포착하지 못할 가능성이 있다. 또한, 두 모델 라우팅에서는 보조 모델의 성능이 기본 모델보다 현저히 우수해야 실제 이득을 얻을 수 있다는 점이 실무 적용 시 고려되어야 한다. 향후 연구에서는 비선형 제약, 다중 모델 체인, 그리고 동적 임계값 조정 메커니즘을 탐색함으로써 LEC의 적용 범위를 넓히는 방향이 기대된다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리