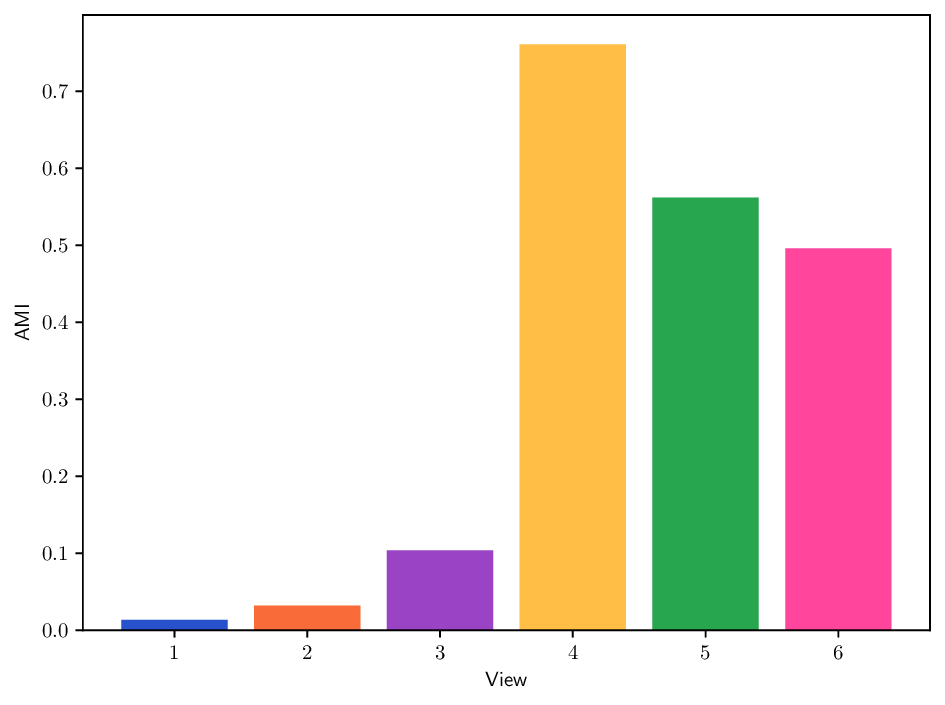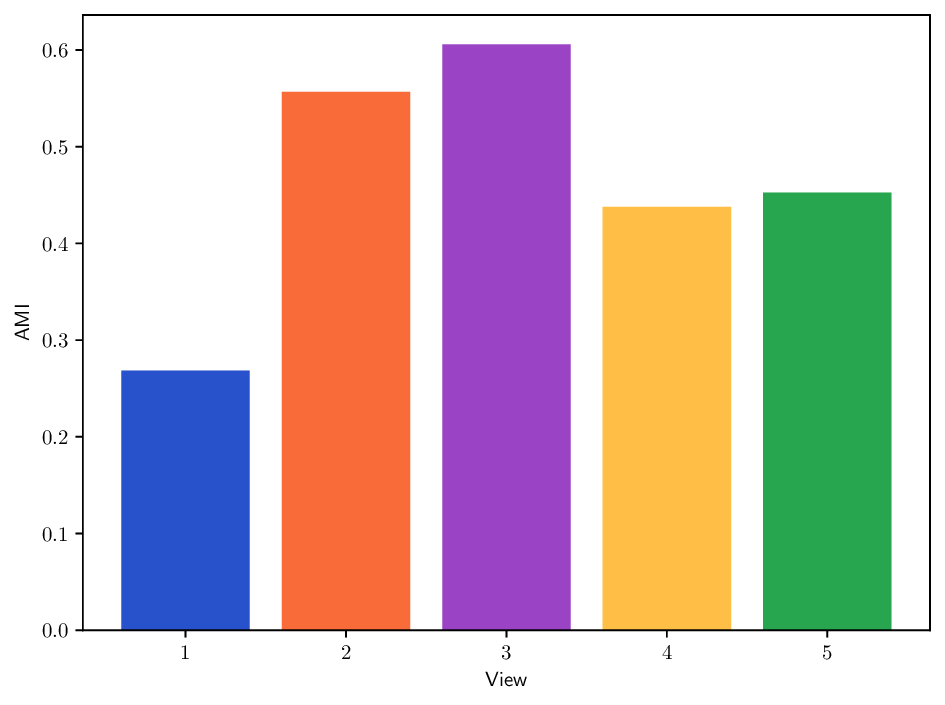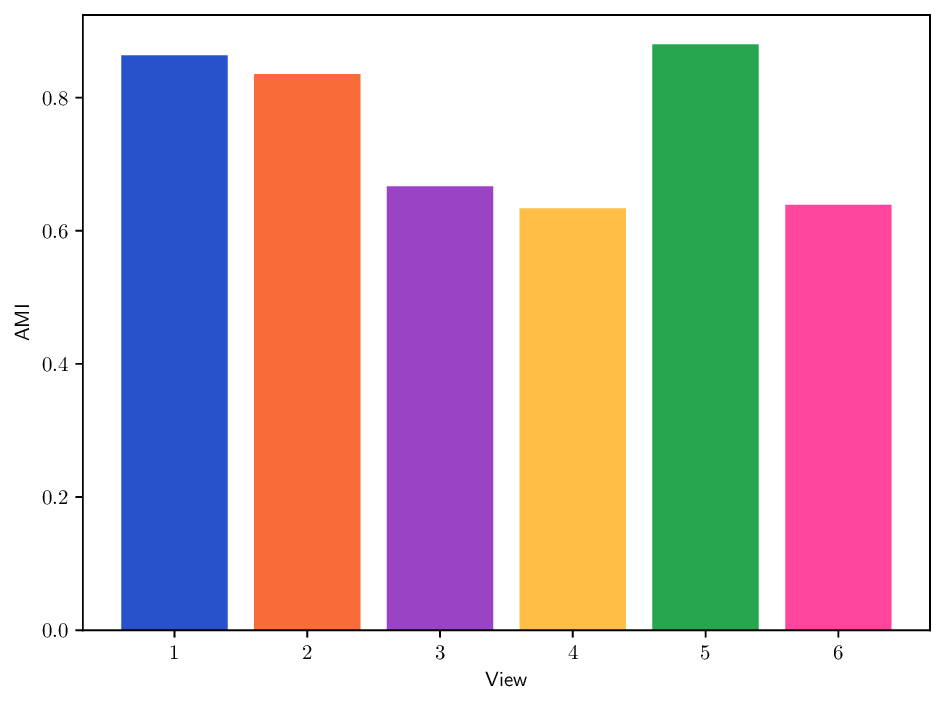다중 뷰 확산 기하학 얽힌 확산 궤적 활용
📝 원문 정보
- Title: Multi-view diffusion geometry using intertwined diffusion trajectories
- ArXiv ID: 2512.01484
- 발행일: 2025-12-01
- 저자: Gwendal Debaussart-Joniec, Argyris Kalogeratos
📝 초록 (Abstract)
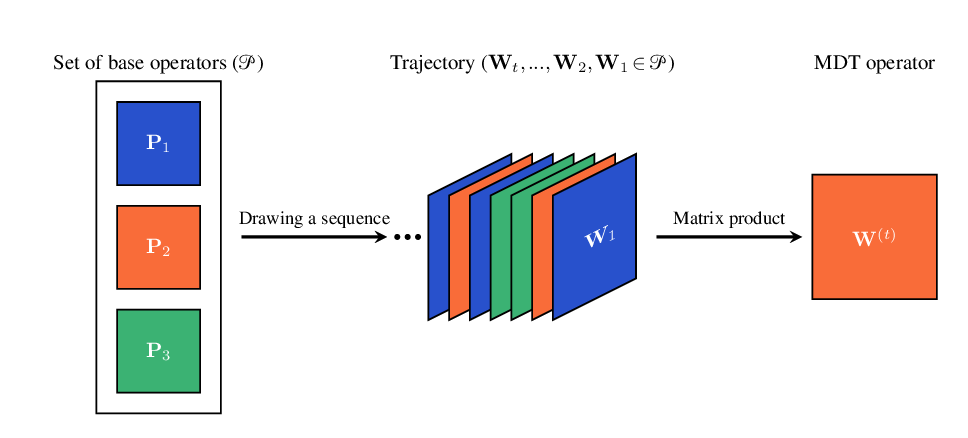
본 논문은 여러 데이터 뷰의 랜덤 워크 연산자를 반복적으로 결합하는 비균질 확산 과정인 얽힌 다중‑뷰 확산 궤적(MDT) 프레임워크를 제시한다. 각 MDT는 궤적에 따라 달라지는 확산 연산자를 정의하며, 이는 확률적·기하학적 해석을 제공해 시간에 따라 뷰 간 상호작용을 포착한다. 제안 방식은 기존 다중‑뷰 확산 모델을 포함하면서도 뷰 간 결합을 위한 새로운 자유도를 제공한다. 완화된 가정 하에 점별 연산자와 전체 과정의 에르고딕성을 증명하고, MDT 기반 확산 거리와 특잇값 분해를 이용한 임베딩을 도출한다. 또한 내부 품질 지표에 기반한 MDT 연산자 학습 전략을 제안하며, 무작위 MDT와의 비교를 통해 확산 기반 방법의 중립적 기준을 제공한다. 실험에서는 매니폴드 학습 및 군집화 과제에서 MDT 연산자가 실질적인 성능 향상을 가져옴을 확인한다.💡 논문 핵심 해설 (Deep Analysis)
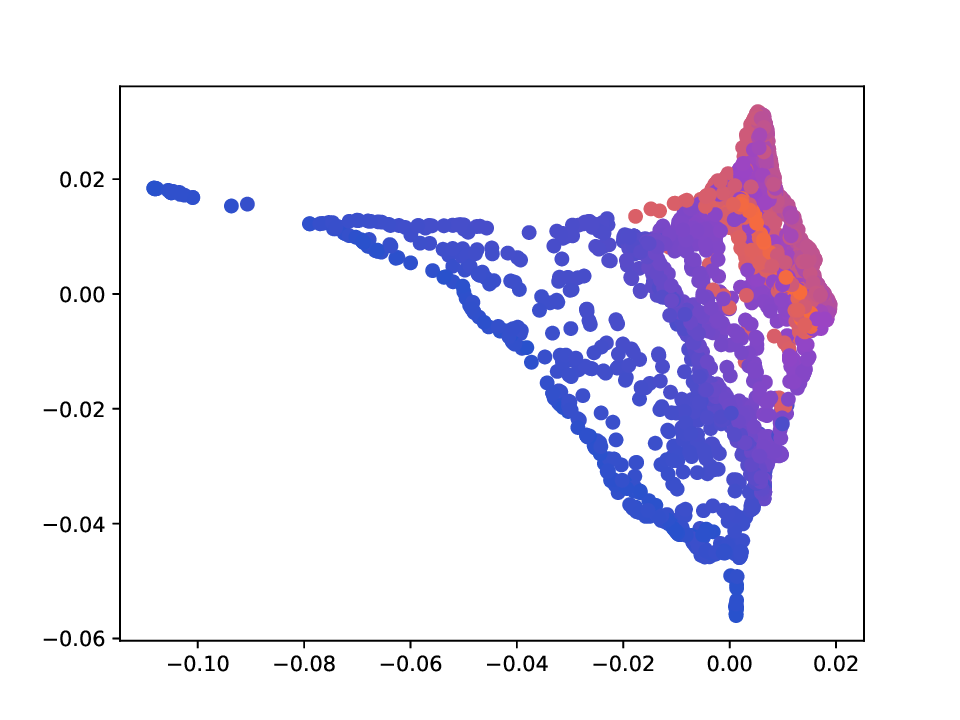
논문은 두 가지 주요 이론적 결과를 제시한다. 첫째, 점별 연산자(trajectory‑dependent operator)가 에르고딕성을 만족한다는 증명이다. 이는 충분히 긴 시간 후에 어떤 초기 상태에서도 동일한 정규화된 분포에 수렴한다는 의미이며, 다중 뷰가 서로 다른 스케일이나 노이즈 수준을 가질 때도 안정적인 확산을 보장한다. 둘째, 전체 확산 과정 자체가 에르고딕함을 보이며, 이는 전체 마코프 체인의 전이 행렬이 시간에 따라 변하지만, 장기적인 평균 동작이 고정된 불변분포를 갖는다는 것을 의미한다. 이러한 성질은 MDT가 기존의 고정 연산자 기반 방법보다 더 강건한 클러스터링 및 매니폴드 복원에 기여할 수 있음을 시사한다.
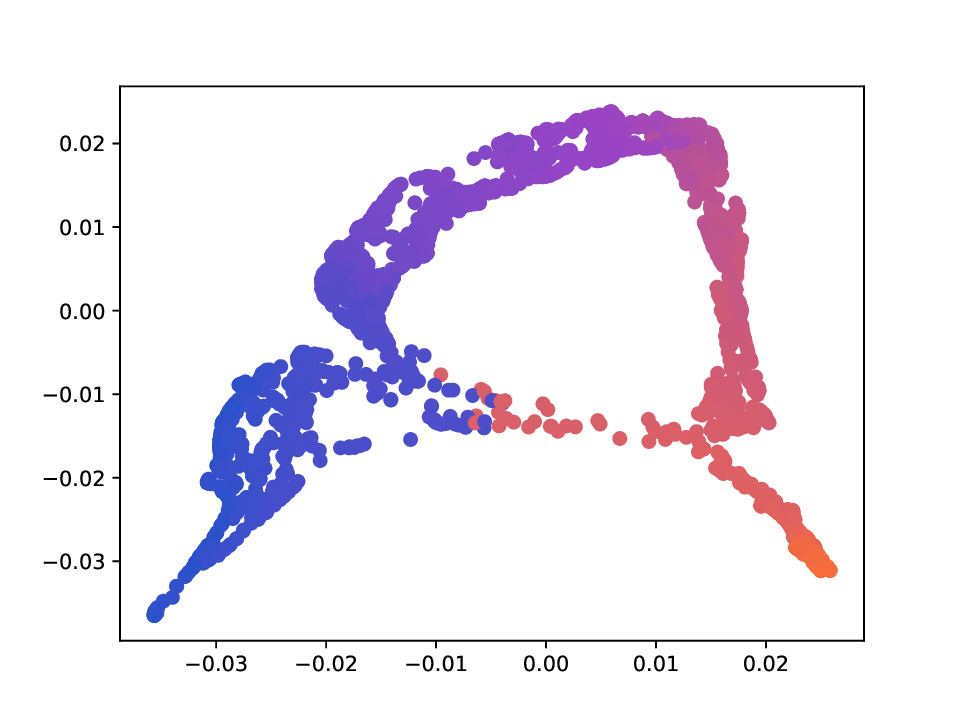
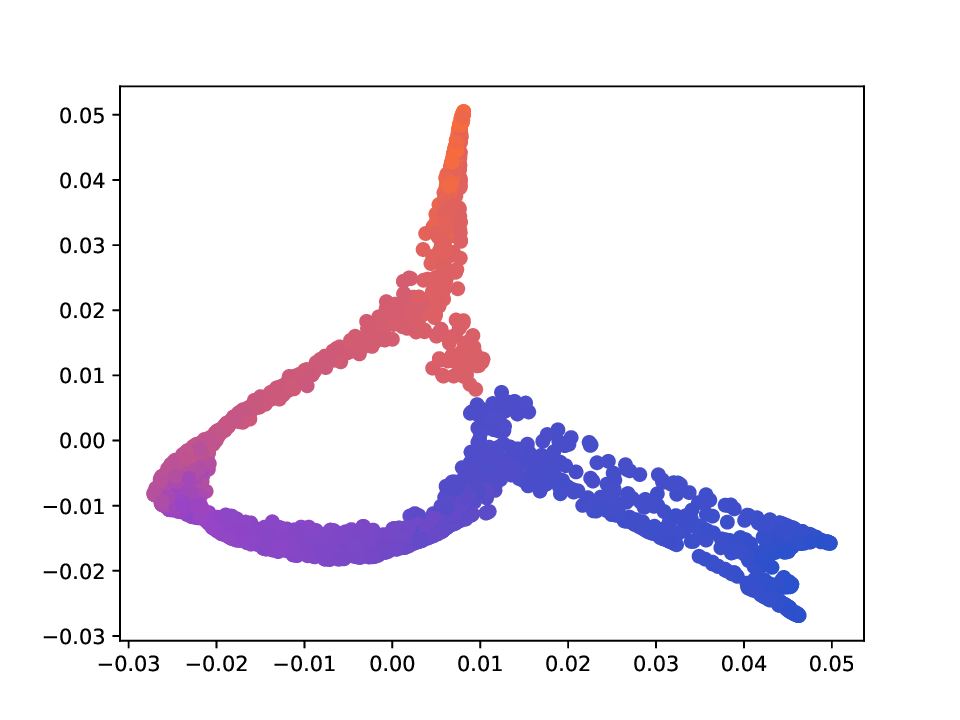
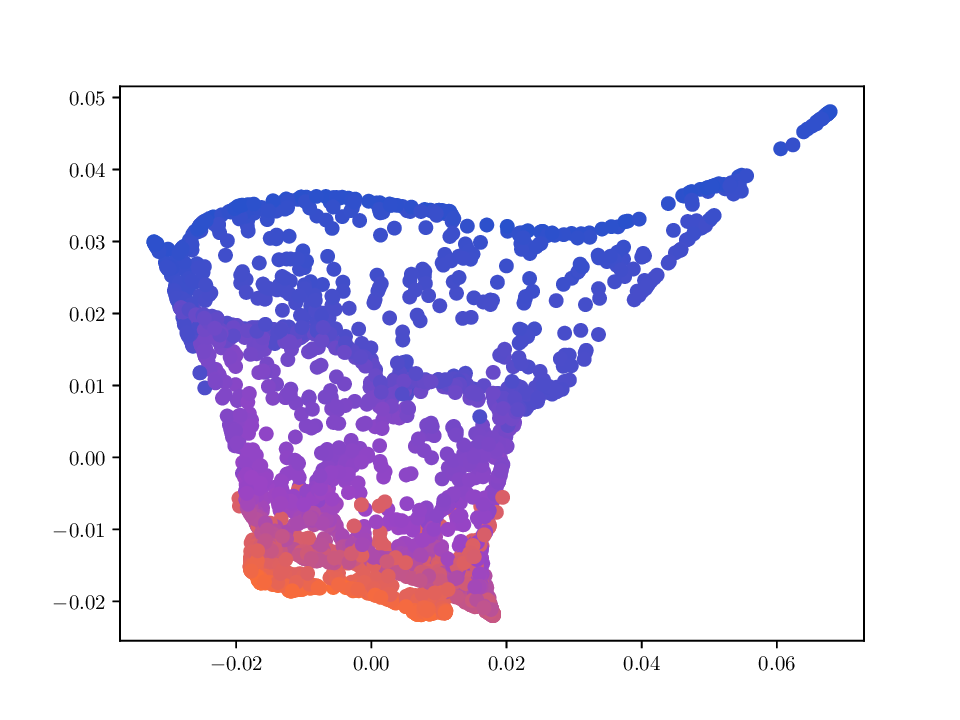
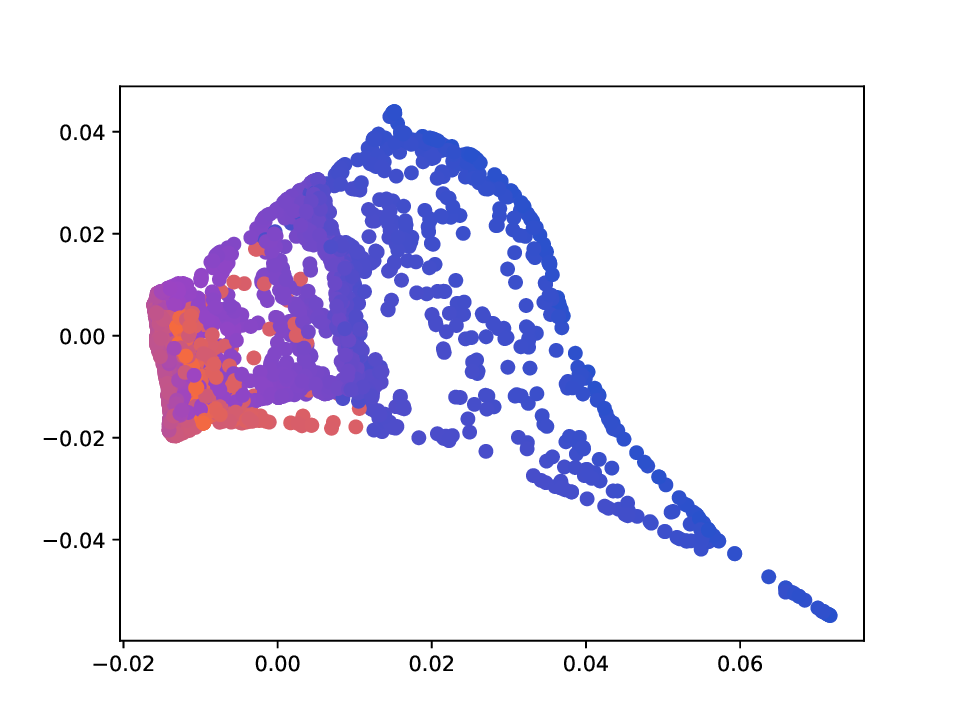
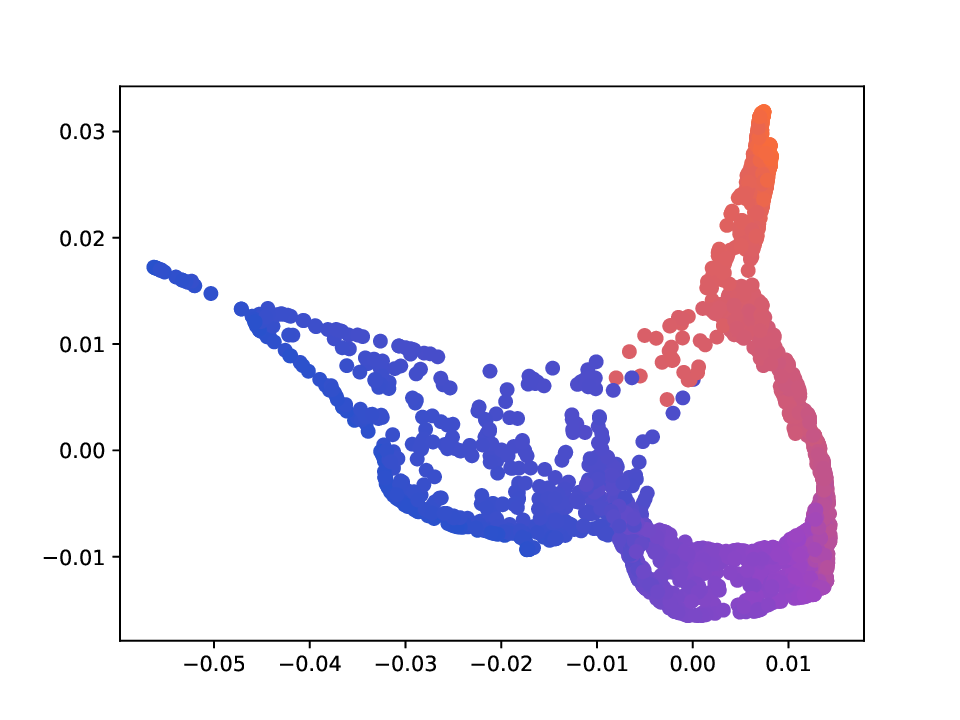
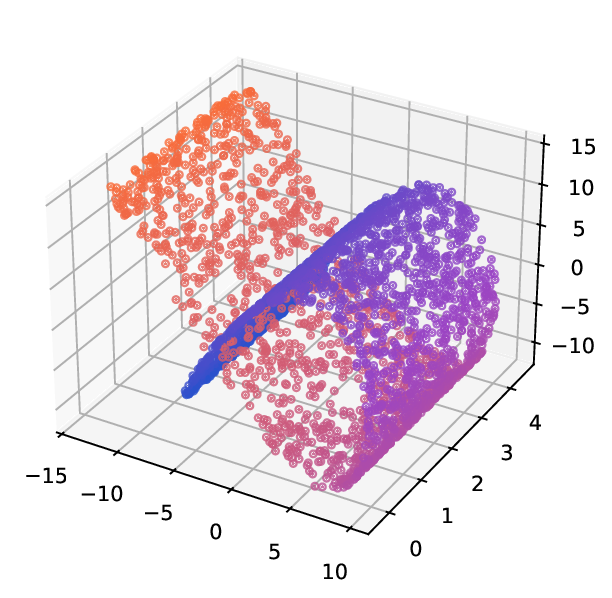
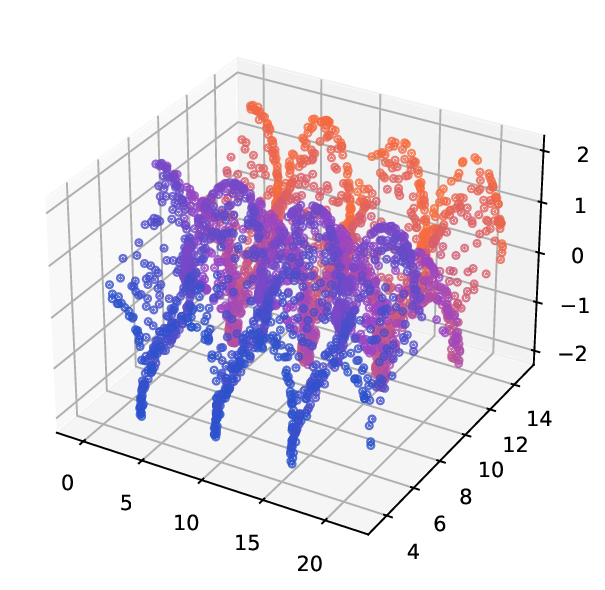
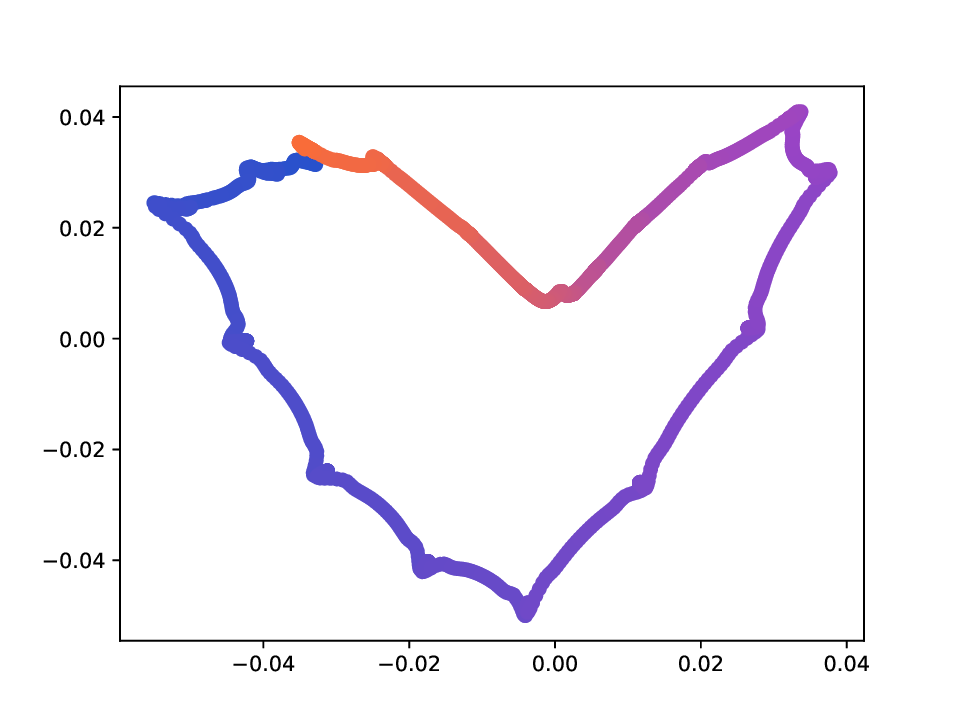
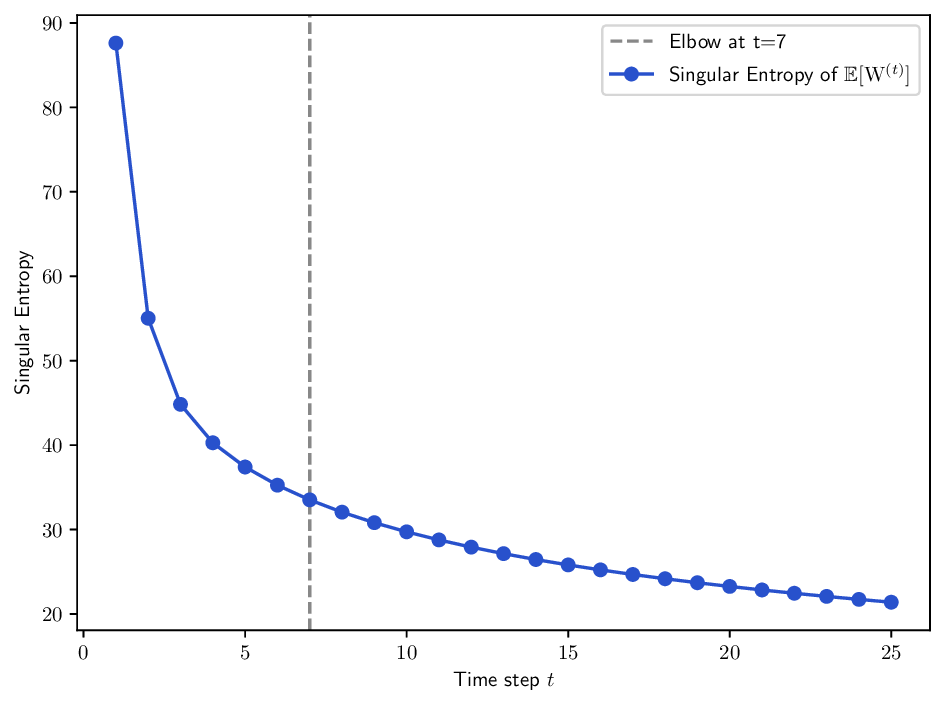
또한 저자는 MDT 기반 확산 거리(diffusion distance)를 정의하고, 이를 특잇값 분해(SVD)를 통해 저차원 임베딩으로 변환하는 절차를 제시한다. 여기서 핵심은 각 단계에서 얻어지는 전이 행렬들의 곱을 하나의 누적 연산자로 보는 것이며, 이 누적 연산자의 스펙트럼을 분석함으로써 데이터 포인트 간의 내재적 거리 구조를 추출한다. 기존의 확산 맵(Diffusion Map)과 달리, MDT는 시간에 따라 변하는 연산자를 고려하므로, 임베딩이 뷰 간 상호작용을 반영한 보다 풍부한 표현을 제공한다.
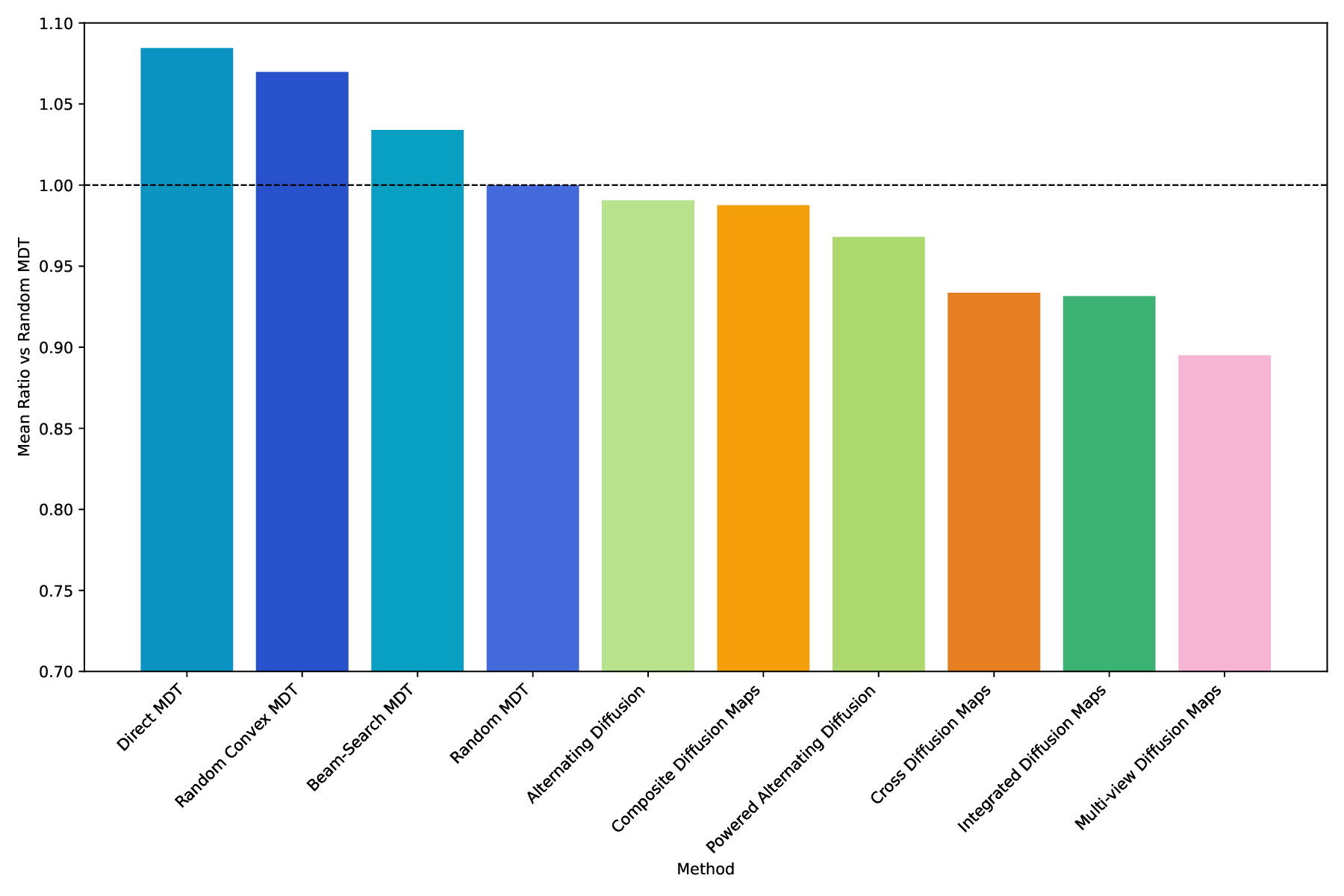
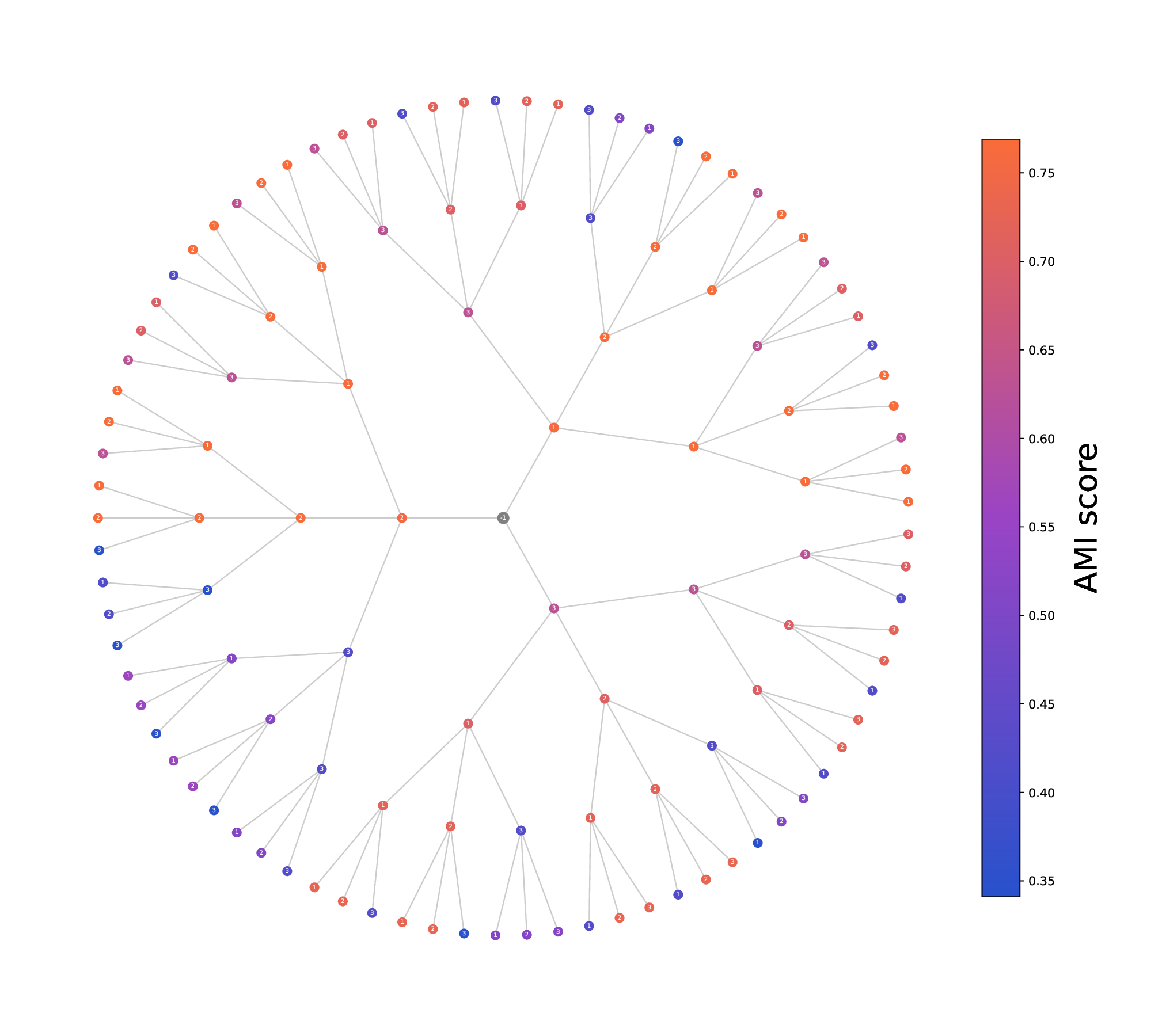
학습 측면에서는 ‘연산자 공간’ 내에서 최적의 MDT 시퀀스를 탐색하기 위한 여러 전략을 제안한다. 내부 품질 지표(예: 마코프 체인의 혼합 속도, 라플라시안 스펙트럼의 갭, 혹은 클러스터링 지표)를 활용해 후보 MDT를 평가하고, 무작위로 선택된 MDT와의 비교를 통해 베이스라인을 설정한다. 이는 새로운 모델이 실제로 뷰 간 정보를 효과적으로 융합했는지, 혹은 단순히 복잡도만 증가시켰는지를 객관적으로 판단할 수 있게 한다.
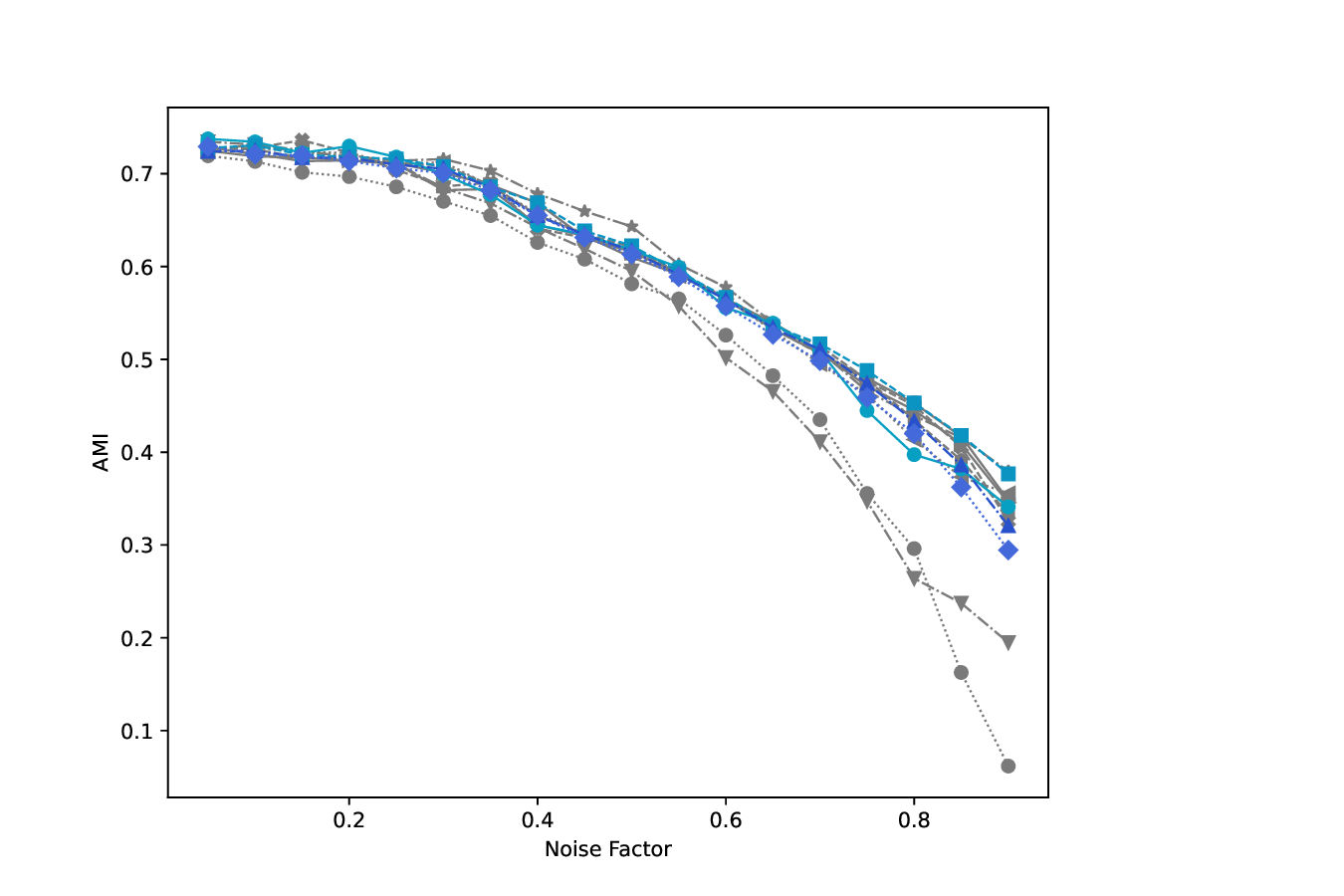
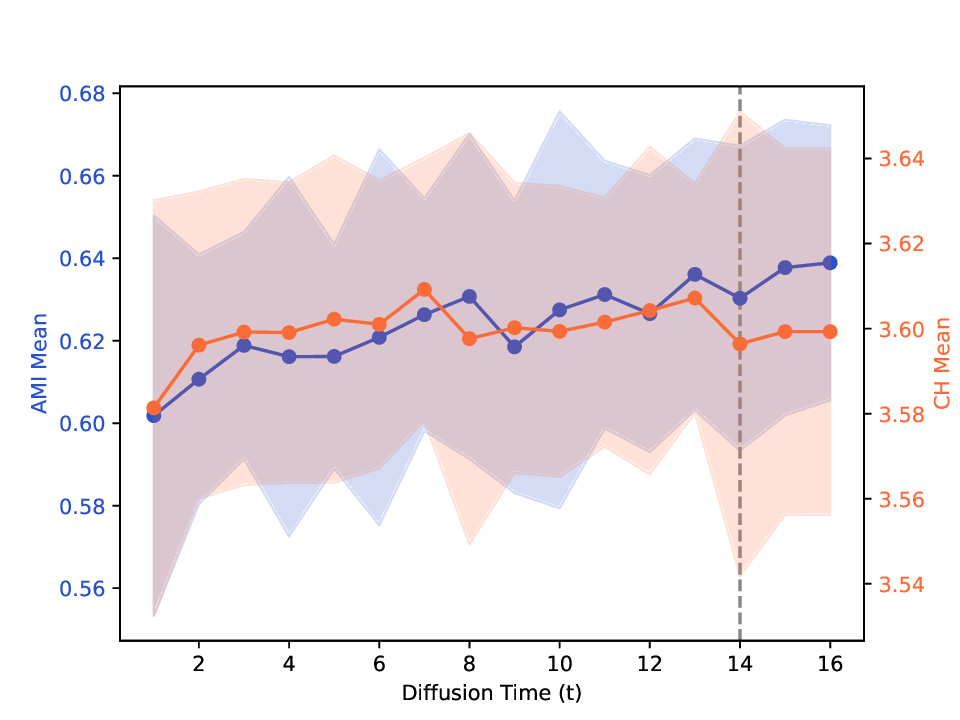
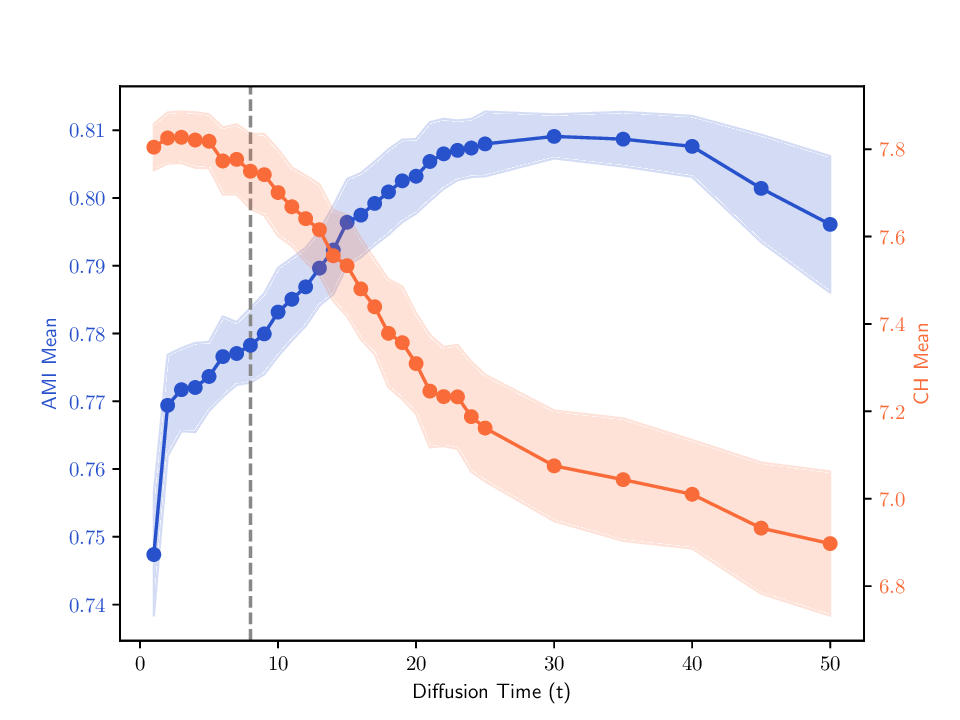
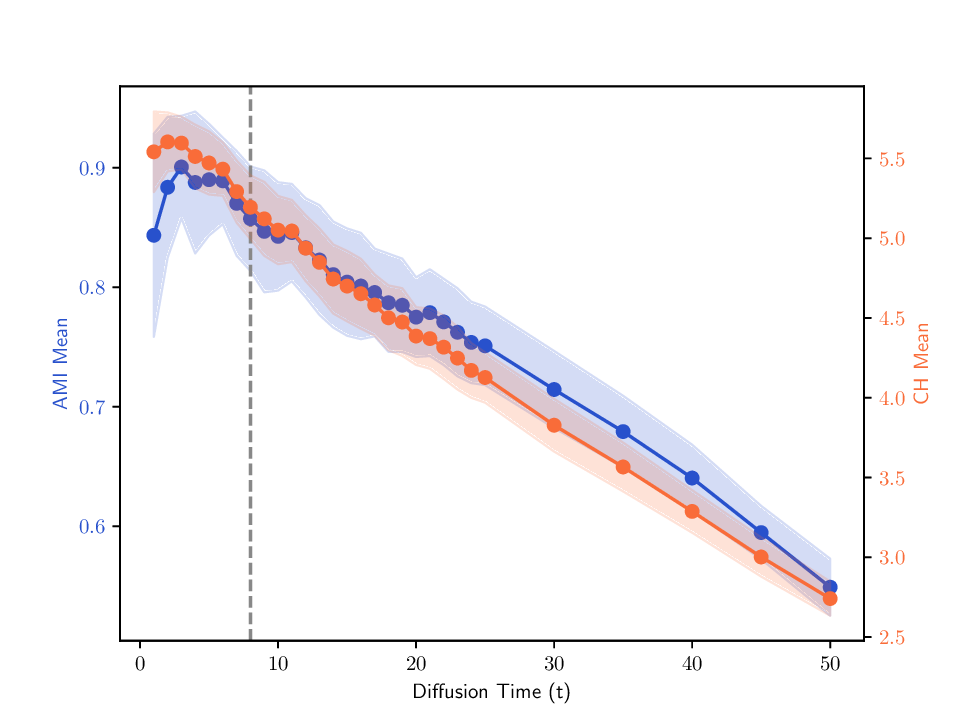
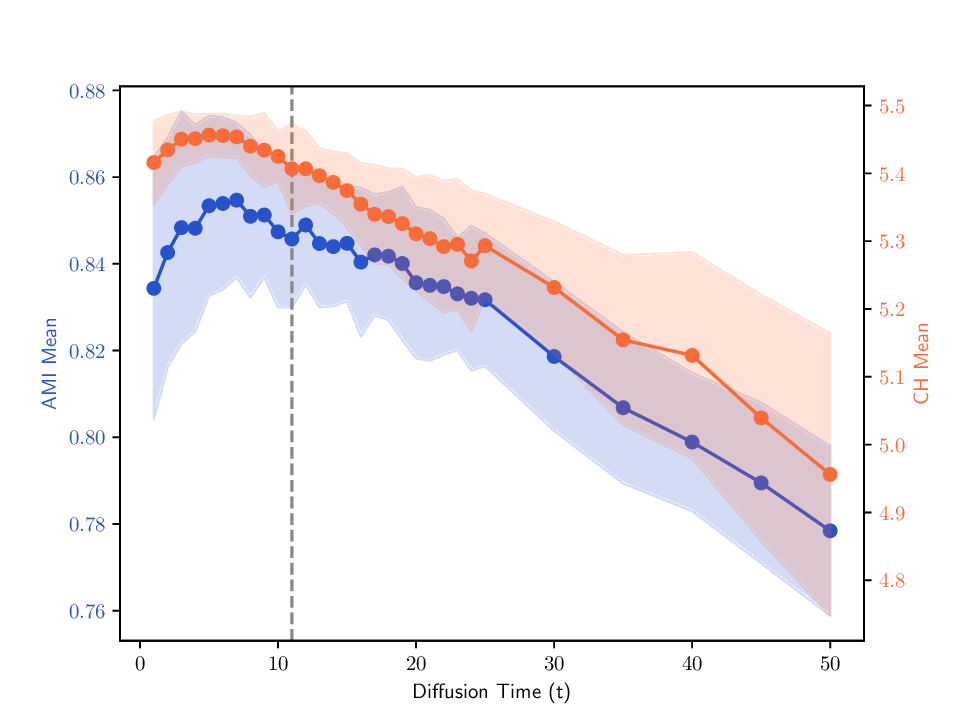
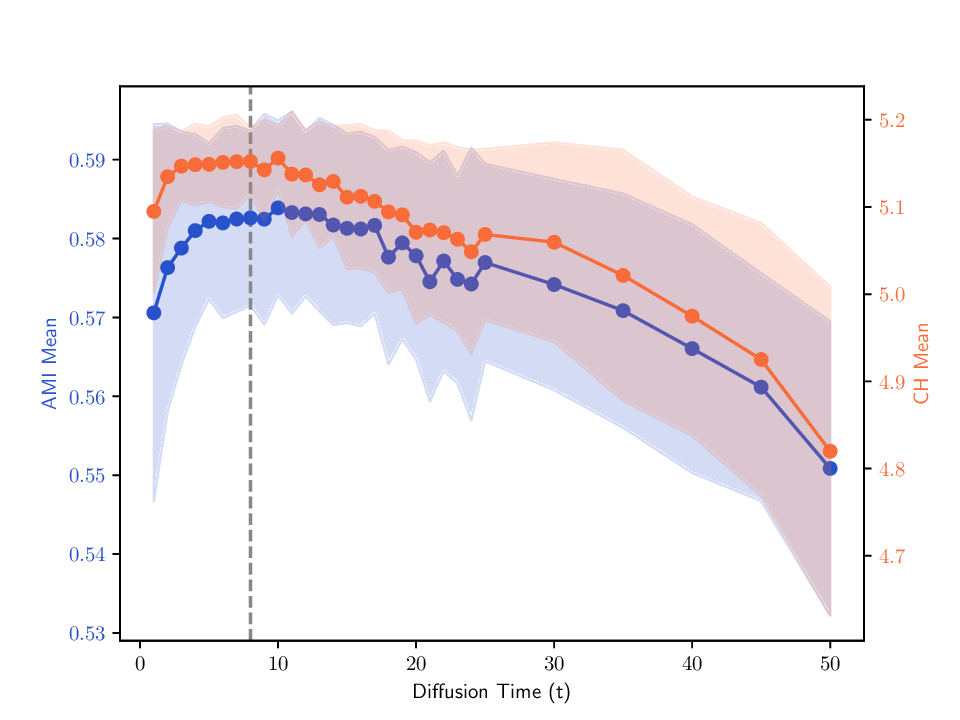
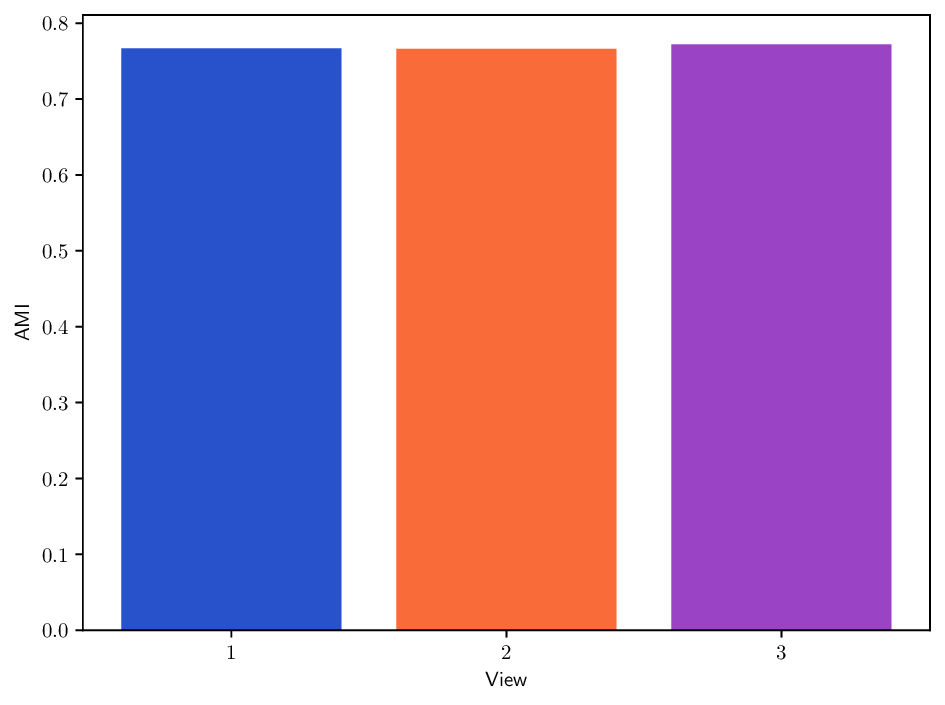
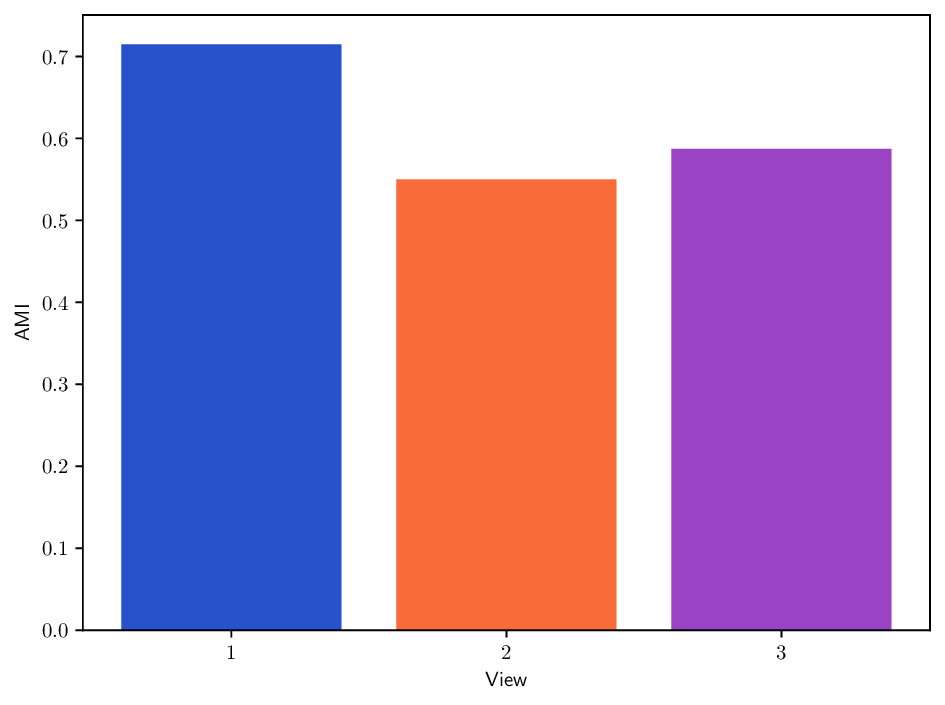
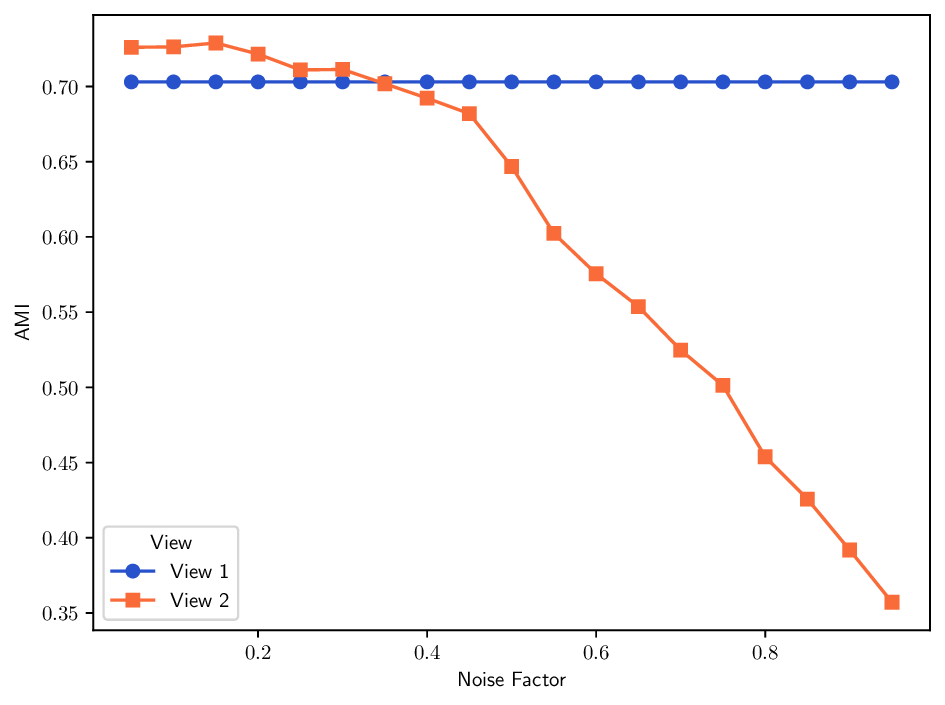
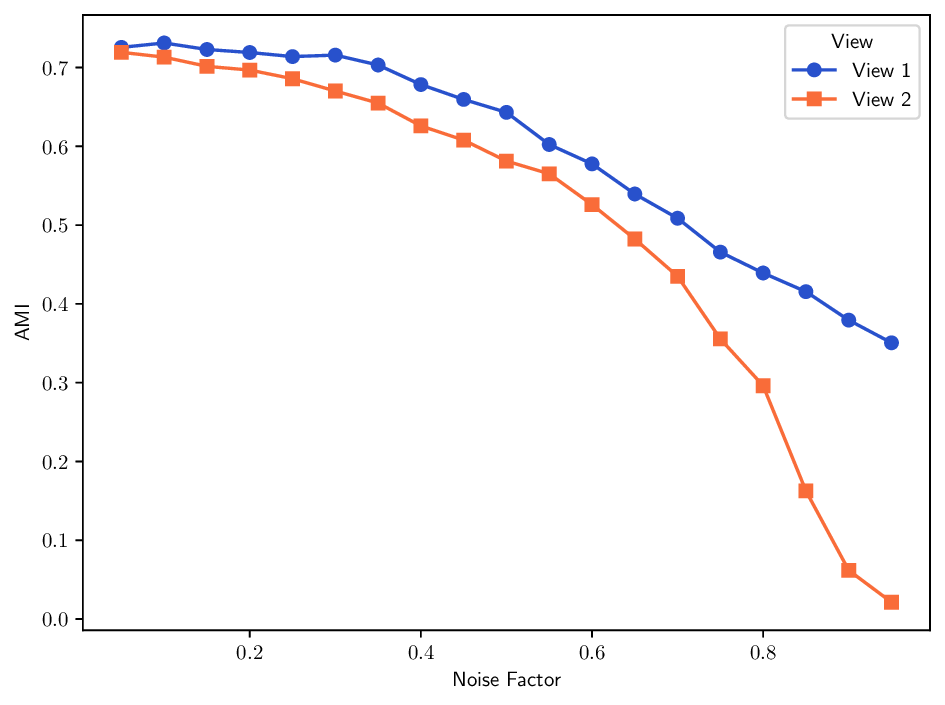
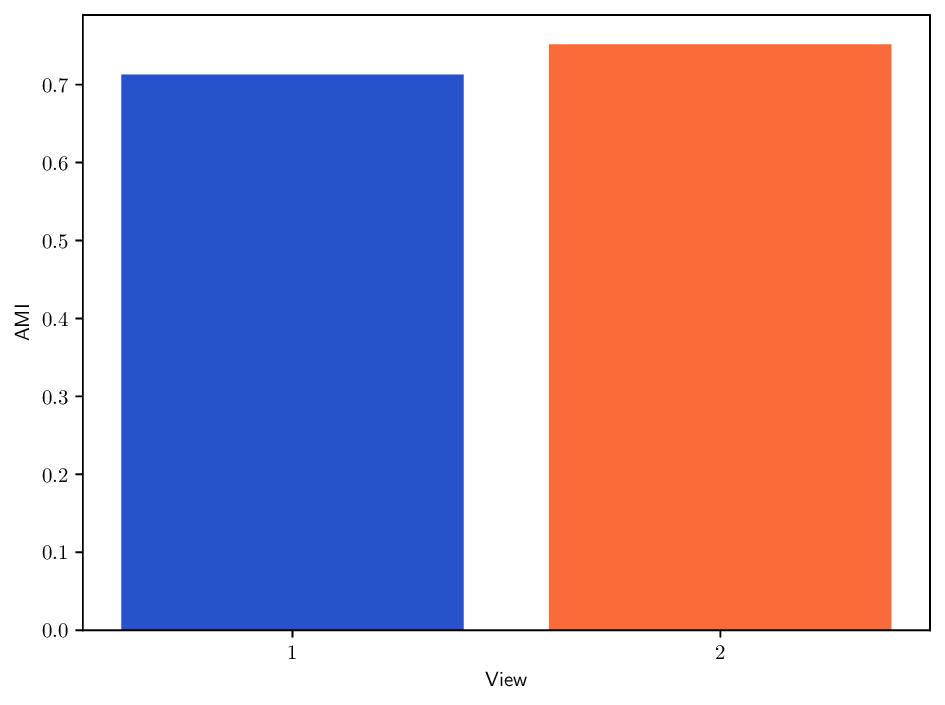
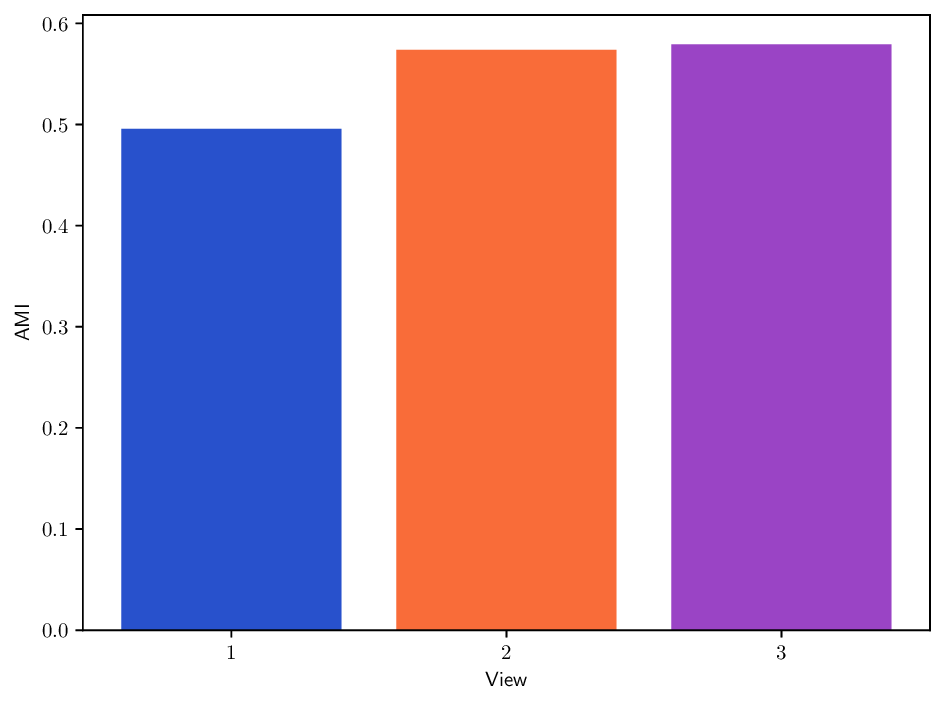
실험에서는 합성 및 실제 데이터셋(예: 다중 센서 이미지, 바이오메디컬 멀티오믹스)에서 매니폴드 학습과 클러스터링 성능을 평가한다. MDT 기반 방법은 기존의 단일‑뷰 확산 맵, 다중‑뷰 정합 방법, 그리고 최근의 그래프 신경망 기반 융합 기법보다 높은 정밀도와 재현율을 기록한다. 특히, 뷰 간 상호보완성이 큰 경우(예: 서로 다른 해상도와 잡음 수준을 가진 이미지)에서 그 이점이 두드러진다. 전반적으로 이 논문은 다중 뷰 데이터의 복합적인 구조를 확산 과정에 자연스럽게 통합하는 강력한 이론적·실용적 프레임워크를 제공한다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리