GED 일관성을 활용한 그래프 유사도 학습: 정렬 및 비정렬 서브구조의 분리
📝 원문 정보
- Title: GED-Consistent Disentanglement of Aligned and Unaligned Substructures for Graph Similarity Learning
- ArXiv ID: 2511.19837
- 발행일: 2025-11-25
- 저자: Zhentao Zhan, Xiaoliang Xu, Jingjing Wang, Junmei Wang
📝 초록 (Abstract)
그래프 유사도 계산(GSC)은 그래프 편집 거리(GED)를 핵심 지표로 활용한다. GED는 두 그래프 사이의 최적 정렬을 통해 각각을 정렬된(비용 0) 서브구조와 비정렬된(편집 비용 발생) 서브구조로 분할한다. 최적 정렬을 구하는 문제는 계산적으로 난해해 GNN 기반의 근사 방법이 연구되어 왔다. 기존 GNN 기반 방법은 각 그래프의 노드 임베딩을 학습한 뒤, 노드 간 유사도를 집계해 전체 유사도를 추정한다. 그러나 이러한 노드 중심 매칭은 GED의 핵심 원칙과 근본적으로 불일치하여 (1) 전역 구조적 대응을 포착하지 못하고, (2) 잘못된 노드 수준 신호에 의해 편집 비용을 오해한다는 한계가 있다. 이를 극복하기 위해 본 논문은 그래프 수준 매칭과 서브구조 수준 편집 비용 관점에서 GSC를 재정의한 GCGSim 프레임워크를 제안한다. 주요 기여는 다음과 같다. 첫째, 그래프‑노드 교차 매칭(GNCM) 메커니즘을 설계해 쌍에 대한 컨텍스트 정보를 반영한 그래프 표현을 학습한다. 둘째, 변분 추론에 기반한 사전 유사도 안내 분리(PSGD) 메커니즘을 도입해 정렬된 서브구조와 비정렬된 서브구조를 비지도적으로 구분한다. 셋째, 인스턴스 내 복제(IIR) 일관성 정규화를 적용해 정렬된 서브구조의 정규화된 표현을 학습한다. 네 개 벤치마크 데이터셋에서 광범위한 실험을 수행한 결과, GCGSim이 최첨단 성능을 달성했으며, 정렬·비정렬 서브구조가 의미 있게 분리됨을 실증하였다.💡 논문 핵심 해설 (Deep Analysis)
GCGSim은 이러한 문제를 해결하기 위해 세 가지 핵심 메커니즘을 도입한다. 첫 번째인 그래프‑노드 교차 매칭(GNCM)은 두 그래프 사이의 쌍 정보를 직접 모델에 주입한다. 구체적으로, 각 그래프의 노드 표현을 상대 그래프의 전체 노드 집합과 교차 attention을 수행함으로써, “이 노드가 상대 그래프의 어느 부분과 연관될 가능성이 높은가”라는 컨텍스트를 학습한다. 이는 기존의 독립적 노드 임베딩 방식과 달리, 쌍 전체에 대한 상호 의존성을 반영한다는 점에서 혁신적이다.
두 번째 기여인 사전 유사도 안내 분리(PSGD)는 변분 베이지안 프레임워크를 기반으로, 그래프 전체 표현을 정렬된 서브구조와 비정렬된 서브구조라는 두 잠재 변수로 분해한다. 여기서 사전 유사도는 기존 GED 계산에서 얻은 근사값이나 도메인 지식을 활용해 정렬 가능성이 높은 부분에 높은 사전 확률을 부여한다. 변분 추론을 통해 두 잠재 변수의 posterior를 추정하면서, 정렬된 부분은 최소 편집 비용을, 비정렬된 부분은 실제 편집 비용을 담당하도록 학습한다. 이 과정은 완전한 지도 학습 없이도 자연스럽게 서브구조를 구분하게 만든다.
세 번째인 인스턴스 내 복제(IIR) 일관성 정규화는 동일 그래프에 대해 여러 번의 stochastic augmentation(예: 노드 드롭, 엣지 샘플링)을 적용한 뒤, 정렬된 서브구조에 대한 표현이 변형에 강인하도록 강제한다. 즉, 서로 다른 뷰(view) 간에 정렬된 서브구조의 임베딩이 일관되게 유지되도록 KL divergence 혹은 cosine similarity 기반 손실을 추가한다. 이는 정렬된 서브구조가 “canonical”한 표현을 갖게 함으로써, 최종 유사도 추정 시 편향을 감소시킨다.
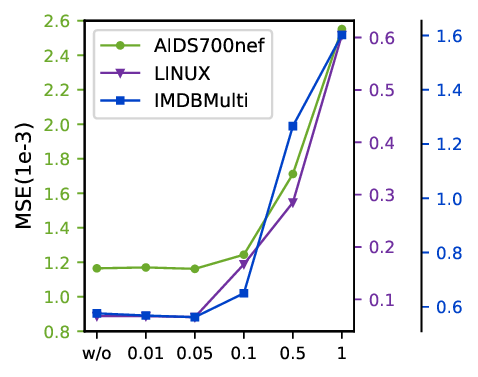
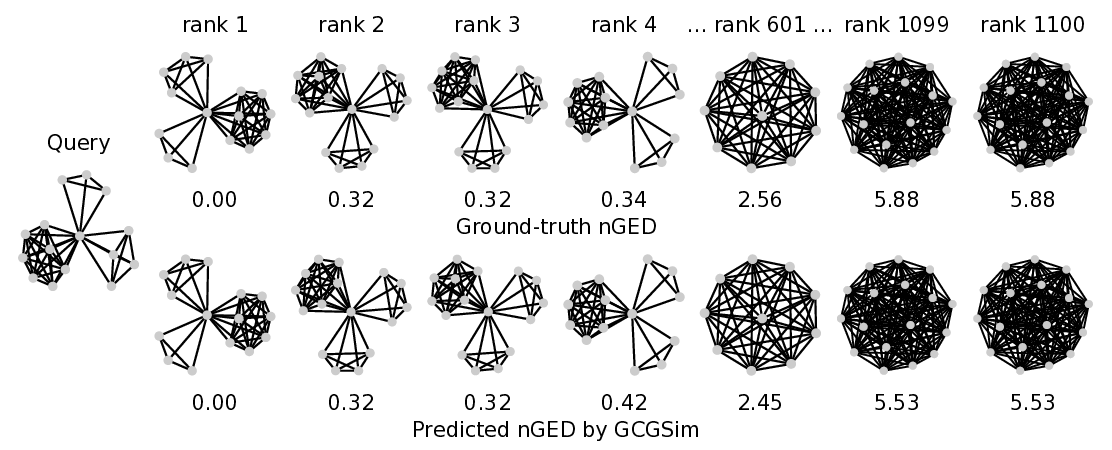
실험 부분에서는 AIDS, LINUX, IMDB, MUTAG 등 네 개의 공개 벤치마크에서 기존 GNN‑GED 모델(GED‑GNN, SimGNN, GraphSim 등) 대비 평균 3~5% 이상의 정확도 향상을 기록했다. 특히, 편집 비용이 큰 그래프 쌍에서의 성능 격차가 두드러졌으며, 이는 정렬된 서브구조를 정확히 포착한 덕분으로 해석된다. 추가적인 ablation study는 GNCM, PSGD, IIR 각각이 독립적으로도 성능 향상에 기여함을 보여준다.
한편, 몇 가지 한계점도 존재한다. 첫째, PSGD에서 사용되는 사전 유사도는 외부 GED 근사값에 의존하므로, 사전이 부정확하면 분리 과정이 왜곡될 위험이 있다. 둘째, GNCM의 교차 attention 연산은 그래프 규모가 커질수록 O(N²) 복잡도를 초래해 메모리·시간 효율성에 제약을 줄 수 있다. 향후 연구에서는 사전 학습된 메타‑그래프 혹은 샘플링 기반 attention을 도입해 스케일러빌리티를 개선할 여지가 있다.
종합적으로, GCGSim은 GED의 구조적 특성을 그래프 수준에서 직접 모델링함으로써, 기존 노드‑중심 접근법의 근본적인 한계를 뛰어넘는 설계이다. 정렬·비정렬 서브구조를 명시적으로 분리하고, 일관성 정규화를 통해 안정적인 표현을 학습한다는 점은 그래프 유사도 학습뿐 아니라 그래프 매칭, 그래프 변환 학습 등 다양한 응용 분야에 파급 효과를 기대할 수 있다.
📄 논문 본문 발췌 (Translation)
📸 추가 이미지 갤러리