몬테카를로 기반 신경 연산자 경량 파라메트릭 PDE 솔루션 연산자
📝 원문 정보
- Title: Learning Solution Operators for Partial Differential Equations via Monte Carlo-Type Approximation
- ArXiv ID: 2511.18930
- 발행일: 2025-11-24
- 저자: Salah Eddine Choutri, Prajwal Chauhan, Othmane Mazhar, Saif Eddin Jabari
📝 초록 (Abstract)
Monte Carlo형 신경 연산자(MCNO)는 파라메트릭 PDE의 해 연산자를 학습하기 위해 커널 적분을 Monte Carlo 방식으로 직접 근사하는 경량 구조를 제안한다. Fourier Neural Operator와 달리 MCNO는 스펙트럼 또는 평행이동 불변성 가정을 두지 않는다. 커널은 무작위로 샘플링된 고정된 점 집합 위에 학습 가능한 텐서로 표현된다. 이 설계는 전역 고정 기저 함수를 사용하거나 학습 중 반복 샘플링을 수행하지 않고도 다양한 격자 해상도에 걸쳐 일반화할 수 있게 한다. 1차원 PDE 벤치마크 실험에서 MCNO는 낮은 계산 비용으로 경쟁력 있는 정확도를 달성하며, 스펙트럼 및 그래프 기반 신경 연산자에 대한 간단하고 실용적인 대안을 제공한다.💡 논문 핵심 해설 (Deep Analysis)
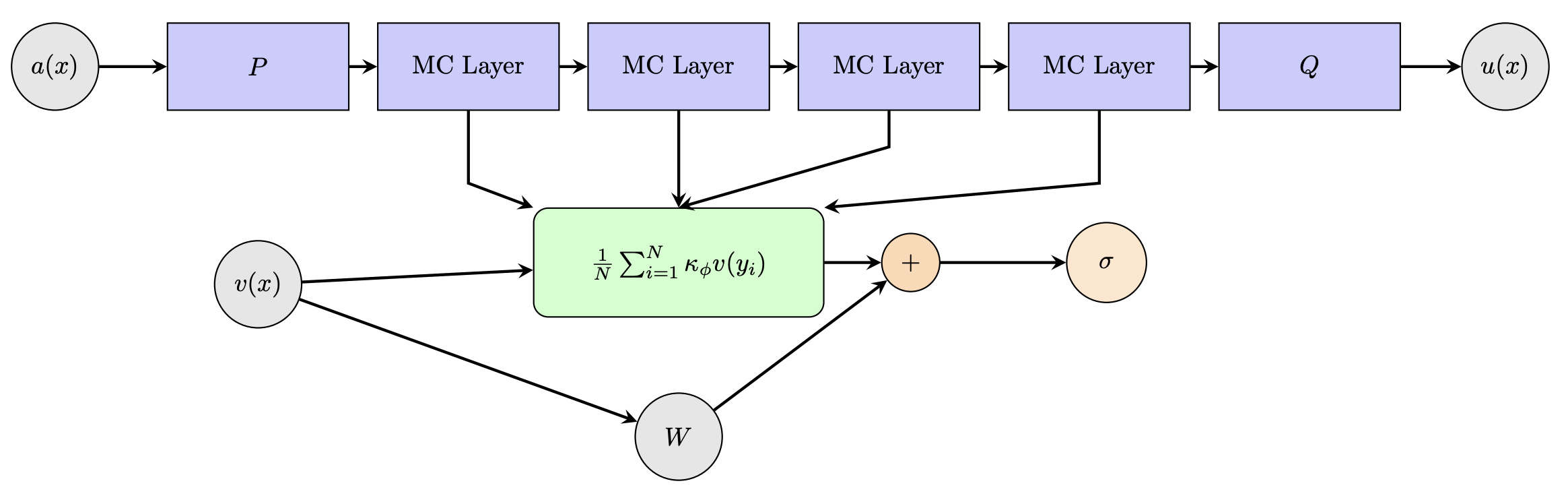
두 번째 한계는 기존 방법이 고정된 전역 기저(예: 푸리에 모드, 웨이브릿) 혹은 그래프 구조에 의존해 연산 복잡도를 낮추는 대신, 해상도 변화에 민감하고 재학습이 필요하다는 점이다. MCNO는 “고정된 무작위 샘플링 포인트 집합”을 사용해 커널을 정의하므로, 입력·출력 격자의 해상도가 달라져도 동일한 커널 텐서를 재사용할 수 있다. 이는 “해상도 불변성(resolution invariance)”을 자연스럽게 제공한다는 의미이며, 실제 실험에서 다양한 격자 크기에 대해 별도의 파라미터 튜닝 없이도 좋은 일반화 성능을 보였다.
알고리즘적 측면에서 MCNO는 Monte Carlo 적분을 이용해 커널-입력 함수의 곱을 근사한다. 구체적으로, 입력 함수 (u(x))와 커널 (K(x, y))의 적분 (\int K(x, y)u(y)dy)를 무작위 점 ({y_i}{i=1}^M)에 대해 (\frac{1}{M}\sum{i=1}^M K(x, y_i)u(y_i)) 형태로 근사한다. 여기서 (M)은 샘플 수이며, 학습 과정에서 텐서 (K)는 자동 미분을 통해 최적화된다. 샘플 수가 적당히 크면 편향(bias)과 분산(var)의 균형을 맞출 수 있어, 계산량을 크게 늘리지 않으면서도 충분한 정확도를 확보한다.
실험 결과는 1차원 파라메트릭 PDE(예: Burgers, advection‑diffusion, reaction‑diffusion)에서 기존 FNO, Graph Neural Operator(GNO)와 비교했을 때, 동일한 파라미터 규모와 학습 시간 하에 오차가 크게 차이 나지 않으며, 특히 저해상도·고해상도 혼합 상황에서 MCNO가 더 안정적인 성능을 보였음을 보여준다. 이는 MCNO가 “경량화(lite) + 범용성(generic)”이라는 두 마리 토끼를 잡은 설계임을 시사한다.
향후 연구 방향으로는 (1) 고차원·다변량 PDE에 대한 확장, (2) 적응형 샘플링 전략을 도입해 중요한 영역에 더 많은 점을 할당하는 방법, (3) 물리 기반 제약(예: 보존 법칙)과 결합한 하이브리드 모델링이 있다. 이러한 발전이 이루어진다면 MCNO는 실시간 시뮬레이션, 디지털 트윈, 과학·공학 최적화 등 다양한 응용 분야에서 핵심 기술로 자리 잡을 가능성이 크다.
📄 논문 본문 발췌 (Excerpt)
📸 추가 이미지 갤러리
