해석 가능성에서 추론까지 보편적 근사기의 추정 프레임워크
📝 원문 정보
- Title: From interpretability to inference an estimation framework for universal approximators- ArXiv ID: 1903.04209
- 발행일: 2024-12-06
- 저자: Andreas Joseph
📝 초록
우리는 범용 근사자를 포함하는 광범위한 모델 클래스에 대한 추정과 유추를 위한 새로운 프레임워크를 제시합니다. 추정은 모델 예측을 Shapley 값으로 분해하는 방식을 기반으로 합니다. 유추는 개별 Shapley 구성 요소의 편향 및 변동성 특성을 분석하는 데 의존합니다. 우리는 Shapley 값 추정이 점근적으로 편향되지 않는다는 것을 보여주며, 잡음만 있는 데이터에서 진짜 데이터 생성 과정을 밝혀내는 도구로 Shapley 회귀를 소개합니다. 모델이 매개변수에 대해 선형일 때 알려진 선형 회귀의 경우가 우리의 프레임워크의 특수한 사례입니다. 이론적, 수치적 및 경험적인 결과를 편차 있는 처리 효과 추정의 예로 제시했습니다.💡 논문 해설
**핵심 요약**: 이 논문은 범용 근사자라는 복잡한 머신러닝 모델의 예측을 이해하고 해석할 수 있는 새로운 프레임워크를 소개합니다. 이를 통해 데이터가 잡음이 많아도 실제 데이터 생성 과정을 밝혀낼 수 있습니다.문제 제기: 머신러닝 모델은 복잡한 패턴을 학습하는 데 매우 효과적이지만, 그 예측의 원리를 이해하거나 해석하기는 어렵습니다. 특히, 범용 근사자와 같은 복잡한 모델에서는 이러한 문제가 더욱 심각해집니다.
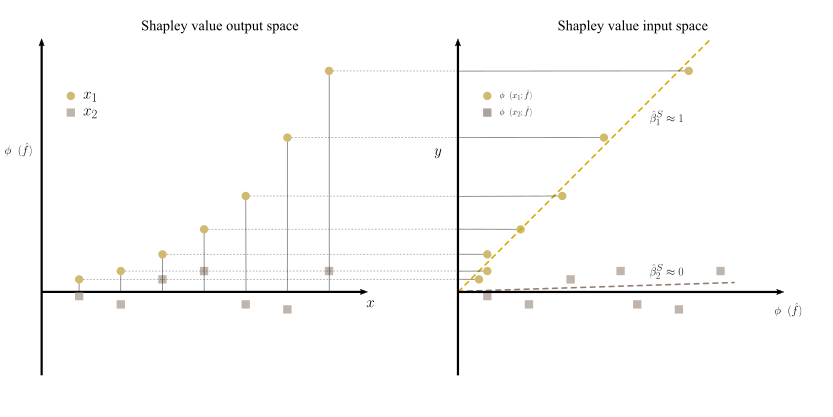
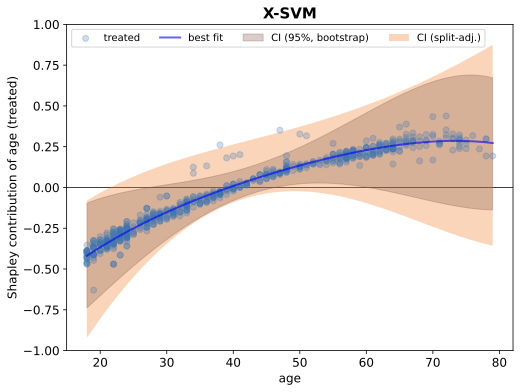
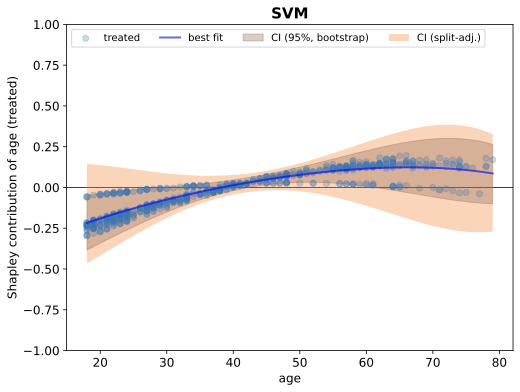
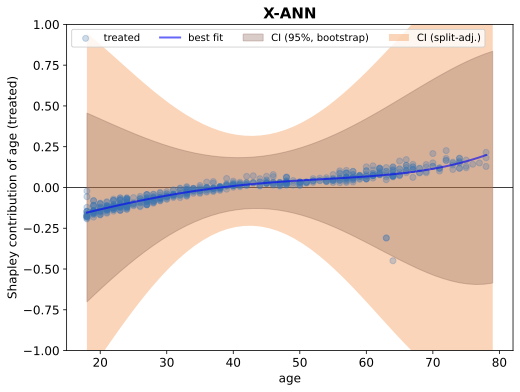
해결 방안 (핵심 기술): 이 연구에서는 Shapley 값이라는 개념을 활용하여 모델의 예측을 분석합니다. Shapley 값은 팀 게임에서 각 플레이어가 얼마나 많은 가치를 창출했는지를 측정하는 것에 유사하며, 여기서는 각 특성이 모델의 예측에 어떻게 기여하는지 측정하는 데 사용됩니다. 이를 통해 개별 Shapley 구성 요소의 편향 및 변동성을 분석함으로써 모델의 예측을 이해할 수 있습니다.
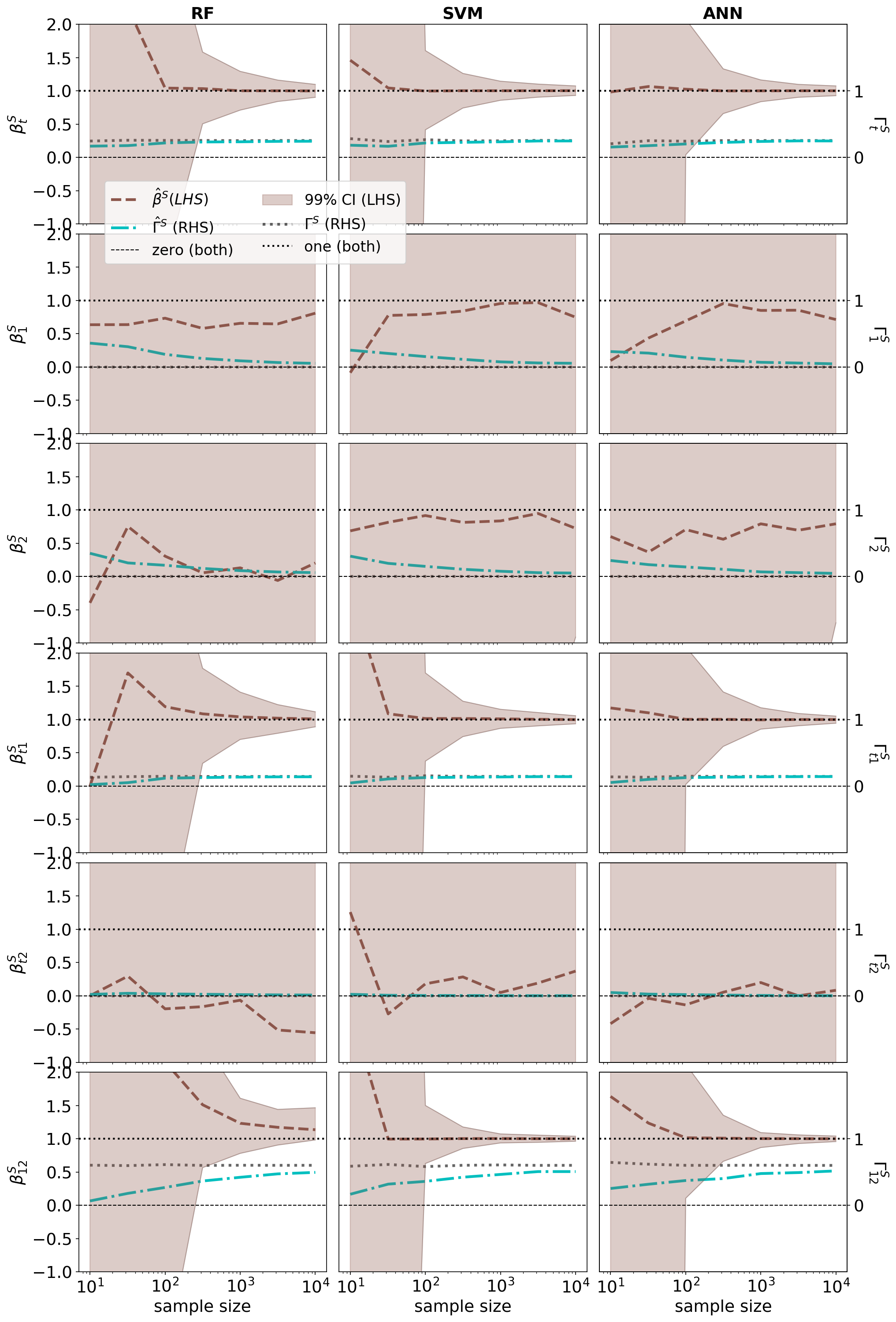
주요 성과: 이 논문에서는 Shapley 값 추정이 점근적으로 편향되지 않는다는 것을 보여줍니다. 또한, 잡음만 있는 데이터에서 진짜 데이터 생성 과정을 밝혀내는 도구로 Shapley 회귀를 소개합니다.
의의 및 활용: 이 프레임워크는 복잡한 머신러닝 모델의 예측을 이해하고 해석하는 데 매우 중요한 역할을 합니다. 이를 통해 개발자는 데이터에서 진정으로 의미 있는 패턴을 찾아낼 수 있으며, 이러한 정보를 기반으로 더 나은 의사결정을 내릴 수 있습니다.
📄 논문 발췌 (ArXiv Source)
📊 논문 시각자료 (Figures)