상관된 확률 변동 요인을 고려한 최적 투자 전략
📝 원문 정보
- Title: Optimal Investment with Correlated Stochastic Volatility Factors- ArXiv ID: 1908.07626
- 발행일: 2022-11-29
- 저자: Maxim Bichuch and Jean-Pierre Fouque
📝 초록
확률적 변동성 요인에 따라 변화하는 주식 환경에서 포트폴리오 배분 문제는 많은 관심을 받고 있다. 단일 임의 요인이 있는 경우 최종 시간까지의 전력 유틸리티를 극대화하는 문제가 고전적인 왜곡 변환을 통해 선형화될 수 있다. 본 논문에서는 여러 요인을 다루기 위해 이들 요인이 완벽하게 상관되는 경우로 줄이는 페르투르베이션 기법을 사용한다. 제안된 근사 방법은 완전 비선형 HJB 방정식 대신 차원이 낮은 두 개의 선형 방정식을 수치적으로 해결하는 것을 요구한다. 하위 및 상위 해를 구성하여 그 차이가 원하는 정확도 순서에 맞는 엄밀한 정확성 결과를 도출한다. 특정 모델에 대해 근사를 위한 명시적 공식이 있는 경우 이 결과를 설명한다. 표기법을 가능한 한 명확하게 유지하기 위해 하나의 주식과 두 개의 요인의 경우를 다루고, 이를 두 가지 주식과 두 가지 요인의 경우로 확장하는 방법을 기술한다.💡 논문 해설
**핵심 요약**: 이 논문은 여러 임의 변동성 요인이 있는 환경에서 최적 투자를 결정하기 위한 새로운 접근법을 제시하고 있다. 이러한 복잡한 시스템에서는 주식 가치와 수익률이 시간에 따라 불확실하게 변동한다.문제 제기: 이 연구는 여러 임의 요인이 있는 환경에서 최적 투자 문제를 해결하려고 한다. 특히, 각각의 요인은 서로 연관되어 있으며 이러한 상관관계가 투자의 결과에 큰 영향을 미친다.
해결 방안 (핵심 기술): 연구진은 이 문제를 단일 임의 요인이 있는 경우로 근사하여 해결한다. 이를 위해, 모든 요인들이 완벽하게 연관되어 있는 상태에서 시작하고, 그로부터 다른 상황을 작은 변화로 접근한다. 이러한 방법으로 복잡한 비선형 방정식 대신 선형 방정식을 사용할 수 있어 계산이 간소화된다.
주요 성과: 연구진은 두 개의 선형 방정식을 해결함으로써 원래 문제를 근사적으로 해결하는 방법을 제시한다. 이 방법의 정확도는 하위 및 상위 해를 사용하여 엄밀하게 검증되었다.
의의 및 활용: 이 접근법은 복잡한 투자 환경에서 최적화 문제를 간단히 해결할 수 있는 가능성을 제시한다. 특히, 금융 시장 분석이나 투자 전략 개발에 유용하게 사용될 수 있다.
📄 논문 발췌 (ArXiv Source)
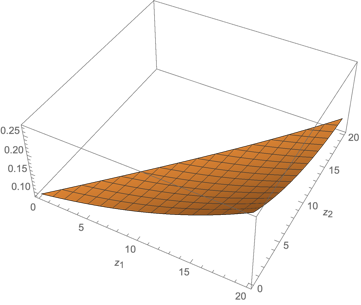
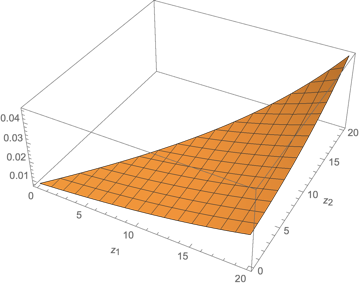
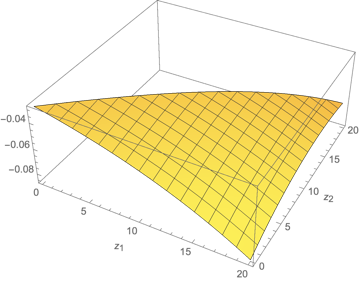
📊 논문 시각자료 (Figures)