합성통제법의 예측구간
📝 원문 정보
- Title: Prediction Intervals for Synthetic Control Methods- ArXiv ID: 1912.07120
- 발행일: 2021-09-09
- 저자: Matias D. Cattaneo and Yingjie Feng and Rocio Titiunik
📝 초록
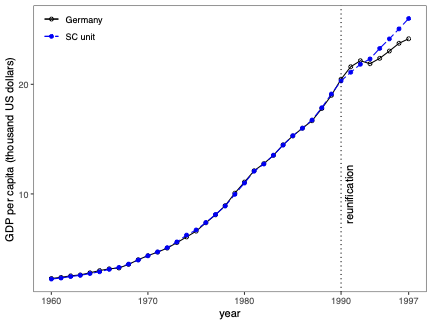
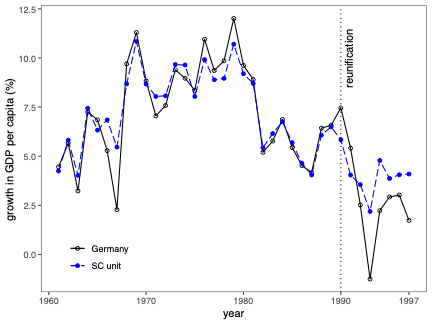
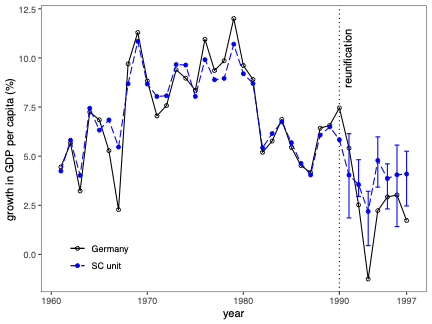
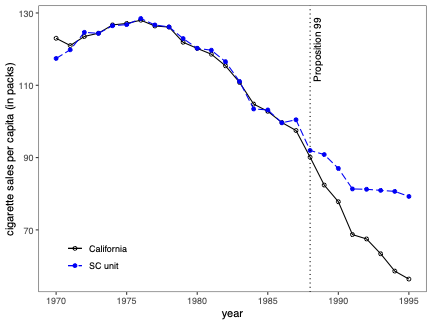
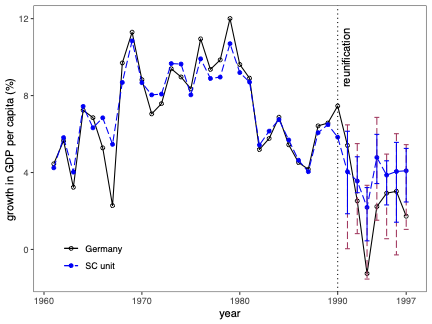
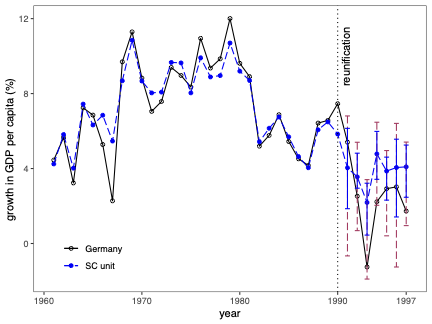
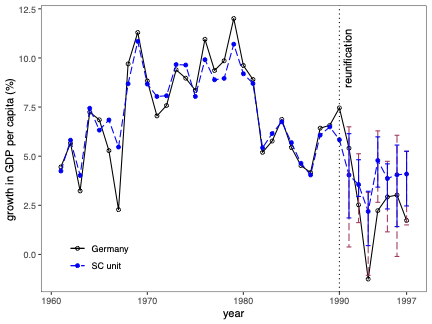
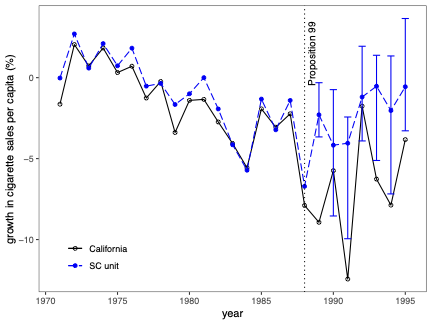
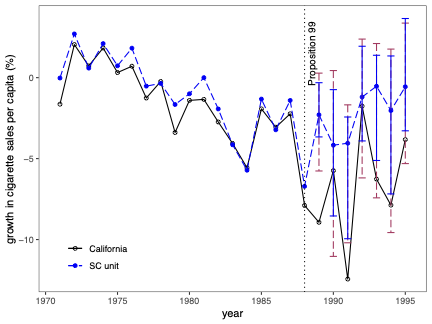
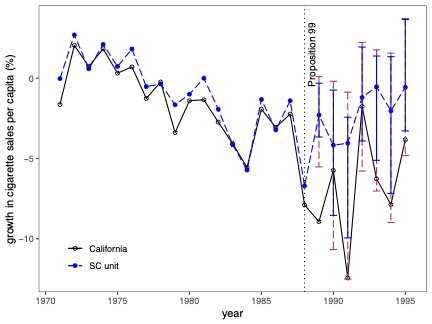
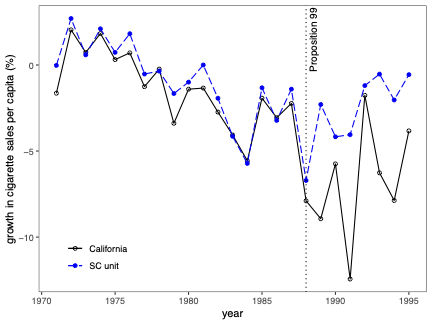
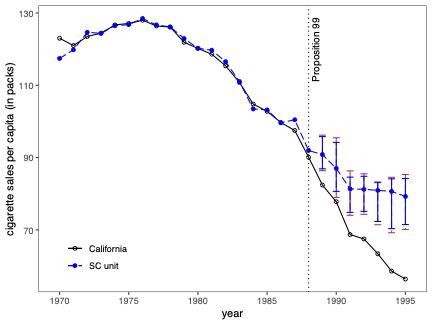
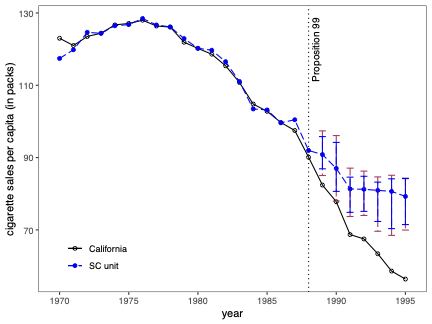
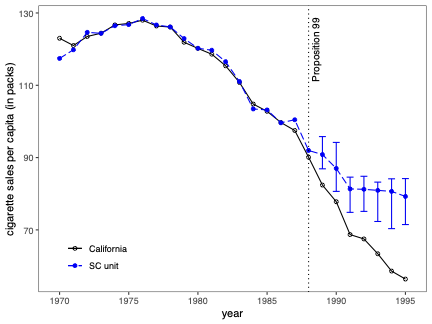
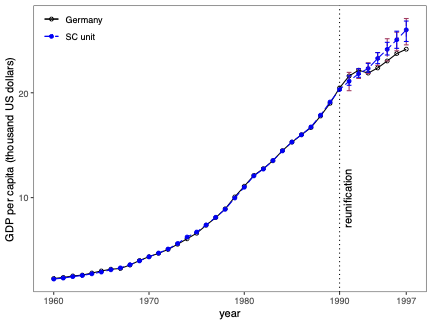
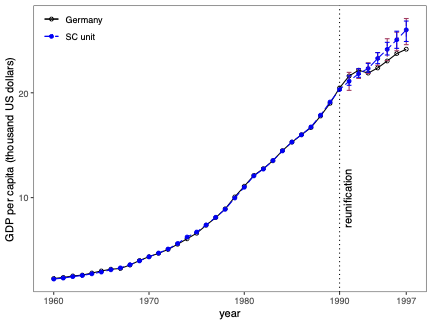
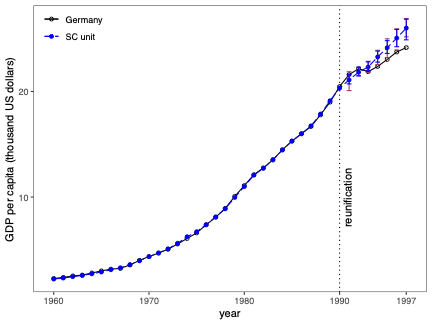
불확실성 측정은 합성 제어(SC) 방법의 분석 및 해석에서 근본적인 문제입니다. 본 연구에서는 SC 프레임워크 내에서 조건부 예측 구간을 개발하고, 이러한 구간이 유한 샘플 확률 보장 제공하는 조건에 대해 논합니다. 제안된 방법은 공변량 조정과 비정상 데이터를 허용합니다. 이 기법의 구성은 SC 예측의 통계적 불확실성이 주치료 전 기간에서 (우리가 추정한) SC 가중치 생성의 무작위성 및 치료 효과 분석 시 후치료 기간에 나타나는 관찰할 수 없는 확률 오차 두 가지 서로 다른 무작위성 소스로 결정된다는 것을 인식하는 것으로 시작됩니다. 따라서 제안된 예측 구간은 이러한 두 가지 무작위성의 원인을 모두 고려하여 구성됩니다. 구현을 위해, 우리는 시뮬레이션 기반 접근법과 유한 샘플 확률 경계 논리로 이루어진 방법을 제안합니다. 이는 원칙적인 민감도 분석 방법으로 자연스럽게 이어집니다. 우리의 방법론의 수치적 성능은 실증적 응용 프로그램 및 작은 시뮬레이션 연구를 사용하여 설명됩니다. \texttt{Python}, \texttt{R} 그리고 \texttt{Stata} 소프트웨어 패키지가 이러한 방법론을 구현합니다.💡 논문 해설
**핵심 요약**: 이 논문은 합성 제어(SC) 방법에서 예측의 불확실성을 측정하는 기법에 대해 다룹니다. SC는 특정 치료 효과를 분석할 때 사용되며, 이 연구에서는 이러한 분석에서 발생하는 두 가지 주요 무작위성 원인을 고려한 예측 구간을 개발합니다.문제 제기: 합성 제어 방법은 특정 정책이나 사건의 효과를 측정하기 위해 사용되는 통계적 기법입니다. 그러나 이 방법에서 발생하는 불확실성을 정확하게 측정하는 것은 어렵습니다. 특히, SC 가중치 생성과 치료 후 오차에 대한 불확실성은 분석 결과에 큰 영향을 미칩니다.
해결 방안 (핵심 기술): 이 논문에서는 두 가지 주요 무작위성 원인을 모두 고려한 예측 구간을 개발합니다. 첫 번째는 치료 전 기간에서 SC 가중치 생성에 대한 무작위성입니다. 두 번째는 치료 후 오차, 즉 실제 데이터와 예측값 간의 차이에 대한 무작위성입니다. 이러한 두 가지 원인을 고려해 예측 구간을 구성하는 방법을 제안합니다.
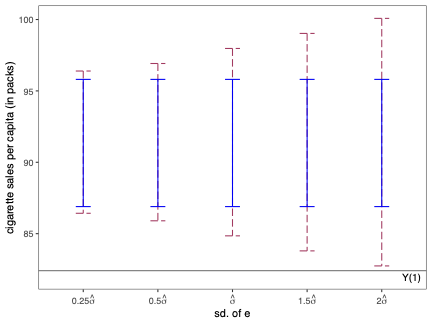
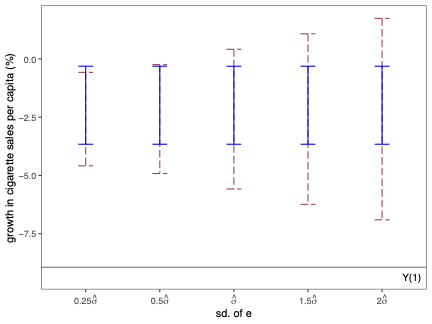
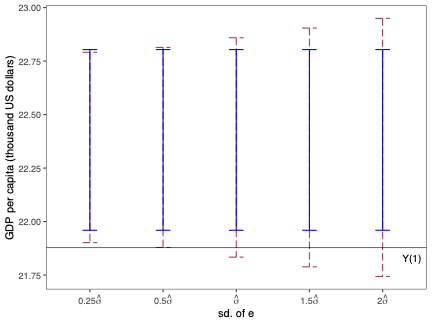
주요 성과: 이 연구에서는 시뮬레이션 기반 접근법 및 유한 샘플 확률 경계 논리를 사용하여 위에서 설명된 예측 구간을 구현했습니다. 또한, 실증적 응용 프로그램과 작은 규모의 시뮬레이션 연구를 통해 제안된 방법론의 수치적 성능을 평가하였습니다.
의의 및 활용: 이 논문은 SC 방법에서 발생하는 불확실성을 정확하게 측정할 수 있는 새로운 접근법을 제공합니다. 이를 통해 치료 효과 분석에 더 큰 신뢰도를 부여하고, 분석 결과의 해석을 더욱 명확하게 만들 수 있습니다. 이는 경제학, 정치학 등 다양한 사회과학 영역에서 중요한 의미를 가집니다.
📄 논문 발췌 (ArXiv Source)
📊 논문 시각자료 (Figures)