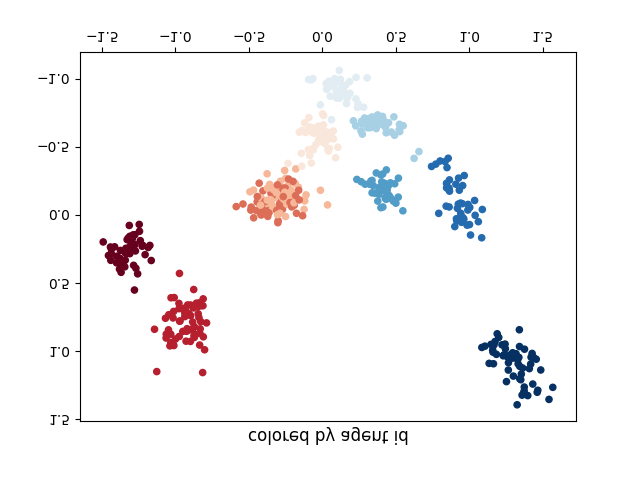
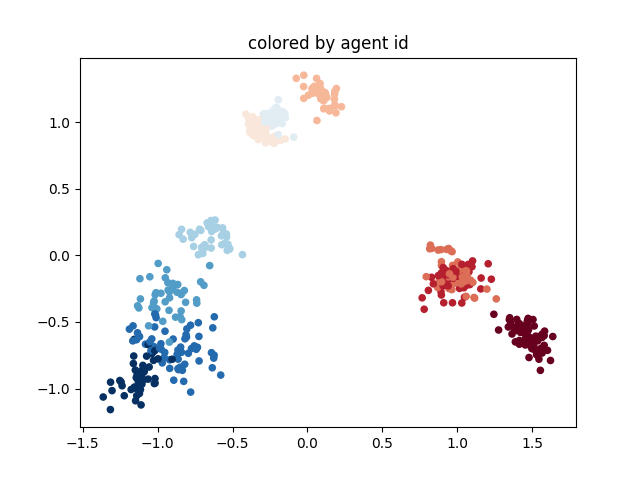
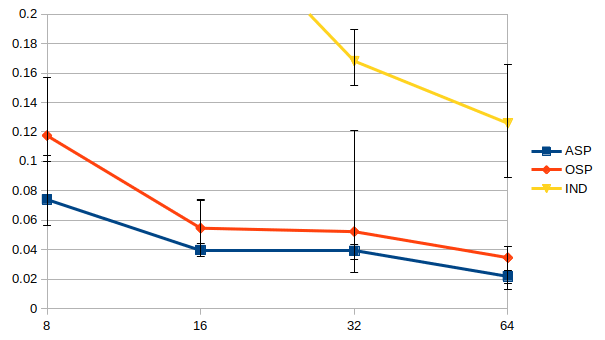
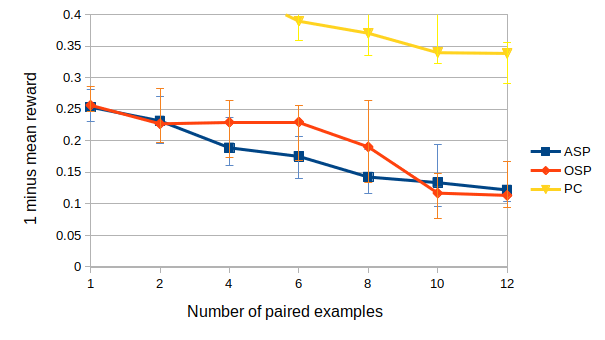
로봇 에이전트는 성공적인 팀원으로서 기존의 사회적 관례를 받아들여야 합니다. 이러한 사회적 관례, 예를 들어 도로의 오른쪽이나 왼쪽을 달리는 것과 같은 것은 최적 정책 중에서 임의적으로 선택된 것입니다. 그러나 성공적인 팀의 모든 에이전트는 동일한 관례를 사용해야 합니다. 이전 연구에서는 기존 에이전트로부터 수집된 입력-출력 데이터와 자가 플레이(Self-play)를 결합하는 방법을 통해 직접 상호작용 없이 사회적 관례를 학습하는 방법을 확인했습니다. 본 논문은 Adversarial Self-Play(ASP)라는 기법을 소개하여 대립적인 훈련을 사용해 배우는 정책 공간을 형성하고 학습 효율성을 크게 향상시킵니다. ASP는 비연관 데이터만 필요로 합니다: 사회적 관례에 의해 생성된 출력의 데이터셋과 연관된 입력이 없는 것입니다. 이론 분석은 ASP가 정책 공간을 어떻게 모델링하는지와 어떤 상황(행동들이 클러스터화되거나 다른 구조를 보이는 경우)에서 가장 큰 혜택을 제공하는지를 밝혔습니다. 세 가지 도메인에 걸친 실험 결과는 ASP의 우수성을 입증합니다: 두 개의 연관 데이터포인트만으로도 원하는 사회적 관례와 더 잘 일치하는 모델을 생성할 수 있습니다.
To solve this problem, the authors introduce Adversarial Self-Play (ASP), a method that uses adversarial training to shape the policy space of robotic agents, enabling them to learn social conventions with minimal data. ASP utilizes unpaired datasets—outputs from existing agents without associated inputs—to train models through an adversarial process where a discriminator distinguishes between model-generated outputs and those produced by actual convention-following agents.
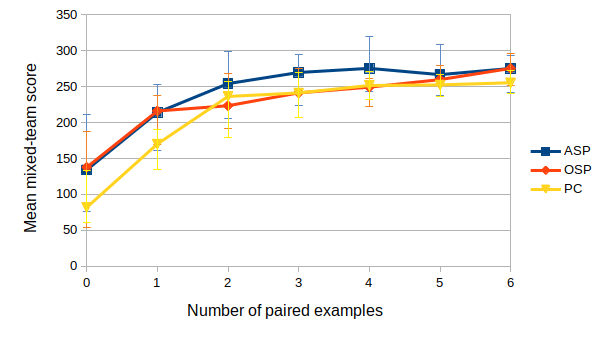
The results demonstrate that ASP can effectively learn desired social conventions even with just a few paired data points, outperforming traditional methods across multiple domains. This method’s effectiveness is particularly notable in scenarios like multi-agent coordination games and speaker-listener tasks where limited interaction data is available.
This work highlights the importance of efficient learning mechanisms for autonomous agents to adapt quickly to new environments or social norms without extensive training datasets. It provides a robust framework that can be applied across various domains, enhancing the ability of robotic agents to collaborate effectively with humans and other AI systems.
# 서론
인간은 성공적인 협업을 위해 사회적 규범에 순응합니다. 예를 들어 프랑스 운전자는 오른쪽 도로를 달리고, 영국 운전자는 왼쪽 도로를 달립니다. 이는 각각의 커뮤니티에서 사회적 관례가 다르기 때문입니다. 그러나 프랑스 운전자는 영국에서의 변화된 관례를 빠르게 이해하고 적응할 수 있습니다. 기존 경험과 새로운 환경 내 다른 운전자들의 행동을 관찰함으로써, 인간은 명시적인 지시만으로도 충분히 이러한 사회적 규범에 순응할 수 있습니다.
로봇이 다중 에이전트 시스템에서 효과적인 팀원으로 작동하려면 프랑스 운전자가 영국에서처럼 기존의 사회적 관례나 규칙을 받아들여야 합니다. 실제로 일상생활에서 인간과 상호작용하는 로봇들은 이미 이러한 관례에 순응하도록 프로그래밍되어 있습니다. 예를 들어, 음성 비서는 의사소통을 위한 언어라는 관례를 사용하고, 자율주행 차량은 도로의 올바른 쪽을 달립니다.
기존 사회적 관례에 맞게 미리 프로그래밍하는 방법은 일부 경우에 효과적이지만, 예상치 못한 상황에는 실패할 수 있습니다. 이론적으로는 학습 기법이 이러한 간극을 메울 수 있지만, 대부분의 다중 에이전트 시스템에서 사회적 관례를 배우는 접근방식(예: 정책 클로닝이나 다른 에이전트와 직접 상호작용)은 매우 많은 양의 데이터가 필요합니다. 그러나 프랑스 운전자는 영국 교통상황을 몇 번만 보고도 왼쪽 도로를 달리는 법을 배우듯, 자율주행 에이전트도 비슷한 조정을 할 수 있어야 합니다.
이전 연구에서는 관찰 증강 자가 플레이(OSP)라는 기법을 소개했습니다. OSP는 제한된 데이터로 사회적 관례를 학습하는 방향으로 한 걸음 나아간 방법입니다. 이들 연구진의 주요 통찰은 자가 플레이와 연관 데이터(주어진 사회적 관례에 따라 생성된 입력과 출력을 사용하여 감독 학습이 가능한 데이터)를 결합한 것입니다.
OSP가 사회적 관례를 배우는 데 있어 획기적인 진전임에도 불구하고, OSP에서 요구하는 연관 데이터를 실제 세계에서 수집하기는 어렵습니다. 앞서 언급된 프랑스 운전자에게 있어서 연관 데이터는 영국 운전자가 고려한 모든 요소와 그에 따른 행동을 의미합니다. 이러한 데이터를 획득하는 것은 불가능할 수 있으며, 인간은 이를 필요로 하지 않습니다. 대신 우리가 원하는 것은 우리의 에이전트들이 인간처럼 영국 도로에서 어떻게 운전해야 하는지를 단순히 관찰하여 배울 수 있도록 하는 것입니다.
본 논문에서는 Adversarial Self-Play(ASP)라는 새로운 기법을 제안합니다. ASP는 사회적 관례에 의해 생성된 출력만을 사용하는 비연관 데이터를 적대적인 훈련(adversarial training)에 활용하여 새로 학습된 에이전트가 원래의 사회적 관례를 받아들일 확률을 높이는 방법입니다. 우리의 방법은 훈련 에이전트와 원하는 사회적 관례로부터 생성된 출력을 구별하려는 판별자(discriminator)를 포함하며, 훈련 에이전트는 판별자를 속이려고 합니다. 자가 플레이(self-play)와 제한적인 연관 데이터와 함께 ASP는 기존 방법보다 사회적 관례에 더 잘 순응하는 에이전트를 일관되게 생성합니다.
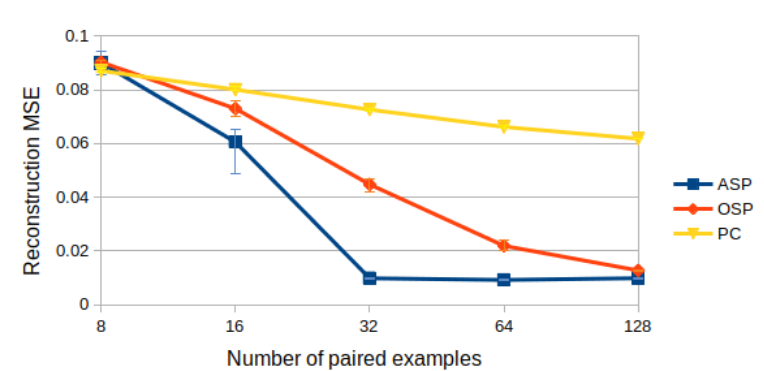
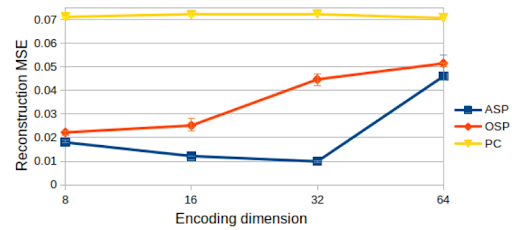
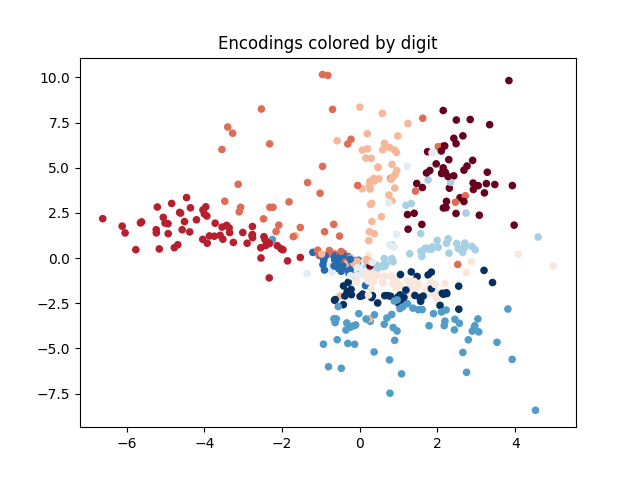
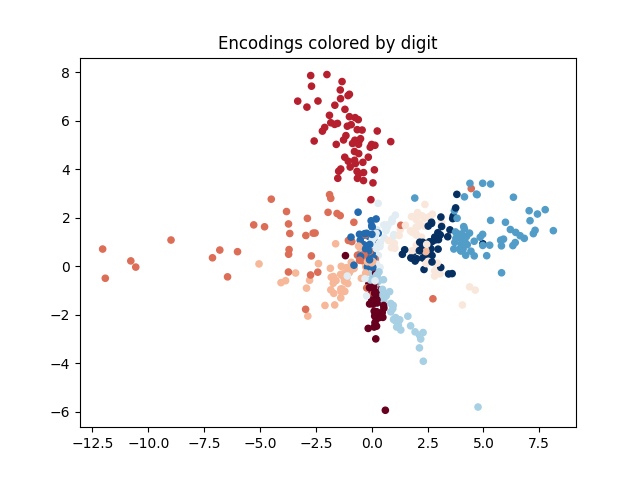
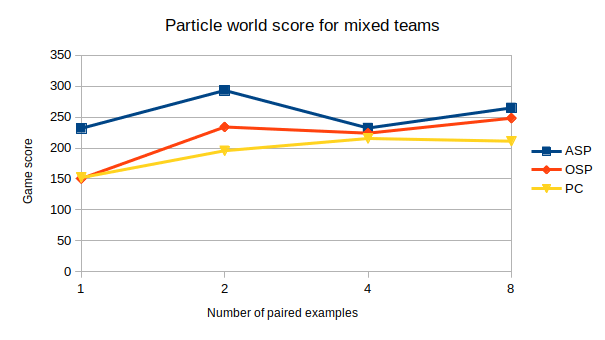
사회적 관례의 적대적 훈련은 충분히 일반화된 접근방식으로, ASP는 에이전트 수나 정확한 작업, 학습 기법과 상관없이 다양한 도메인에 잘 맞습니다. 우리는 세 가지 응용 분야에서 이 방법의 효과를 시연합니다: 시간적 연장 스피커-리스너 도메인, 오토인코더(autoencoder), 그리고 여러 통신 단계가 포함된 다중 에이전트 조정 게임입니다. 우리의 결과는 ASP가 모든 설정에서 개선된 행동을 보여주며, 두 세 개의 연관 데이터 포인트만으로도 가능하다는 것을 나타냅니다.
기초 지식
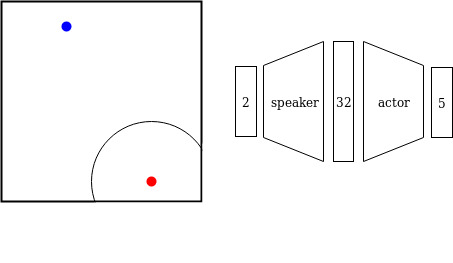
우리는 새로운 에이전트를 훈련시키고자 합니다. 이 에이전트가 팀에 소개되면 전체 팀이 잘 작동해야 합니다. 팀의 작업은 다양할 수 있습니다: 스피커는 리스너에게 특정 위치로 가라고 지시하거나, 여러 에이전트들이 서로 다른 레버를 조정해서 함께 작업을 하는 경우 등입니다. 우리의 관심사에 해당하는 대부분의 작업들은 각 에이전트의 최적 행동이 현재 상태에만 의존하는 다중 에이전트 마르코프 결정 과정(MDP)으로 표현될 수 있습니다. 따라서 우리의 목표는 새로운 에이전트가 혼합 팀의 전체 보상(maximize the overall mixed-team reward)을 극대화하는 정책(policy)를 학습하는 것입니다.
MDP의 정책 학습
단일 에이전트 MDP는 $`\langle S, \allowbreak A, \allowbreak T, \allowbreak R, \allowbreak \gamma\rangle`$와 같은 튜플(tuple)로 표현됩니다. 여기서 $`S`$는 상태 공간(state space), $`A`$는 행동 공간(action space), $`T: S\times A\rightarrow \mathbb P_S`$는 현재 상태와 행동을 다음 상태의 분포로 매핑하는 전이 함수(transition function)이며, $`R: S\times A\times S\rightarrow \mathbb R`$는 실제 값을 생성하는 보상 함수(reward function)입니다. 이 보상 함수는 현재 상태, 현재 행동, 그리고 다음 상태에 따라 결정될 수 있지만 대부분의 문제에서는 일부만 의존할 수 있습니다. $`\gamma\in[0, 1]`$은 미래의 보상보다 현재의 보상을 얼마나 더 선호하는지를 나타내는 할인율(discount factor)입니다.
MDP를 해결하는 목표는 $`\mathbb E_\pi\left[\sum_{t=1}^\infty \gamma^{t-1}r_t\right]`$을 극대화하는 정책(policy) $\pi: S\rightarrow A$를 찾는 것입니다. 여기서 $`r_t`$는 보상 함수 $`R`$에 따라 상태 행동 트레일러(state action trajectory) $`(s_1, a_1, s_2, a_2, ...)`$을 결정하는 전이 함수 $`T`$와 정책 $`\pi`$를 기반으로 계산됩니다.
$`N`$개의 에이전트가 있을 때 각 에이전트 $`i`$는 자신의 행동 집합(action set) $`A_i`$, 그리고 모든 에이전트의 행동을 받아서 다음 상태에 대한 분포를 생성하는 전이 함수 $`T: S\times \prod_{i=1}^N A_i\rightarrow \mathbb P_S`$가 있습니다. 각 에이전트는 자신의 보상 함수 $`R_i`$를 가지고 있으며, 이는 공동 행동에 따라 달라질 수 있습니다. 따라서 각 에이전트의 목표는 개별적인 보상을 극대화하기 위해 자기만의 정책 $\pi_i: S\rightarrow A_i$를 학습하는 것입니다.
우리는 협력적인 환경에서 일하고 있기 때문에, 모든 에이전트가 공유하는 단일 보상 함수 $`R`$을 사용합니다.
혼합 팀 보상
이전 섹션에서는 MDP에 대한 최적 공동 정책 학습 문제를 구성했습니다. 그러나 본 논문은 혼합 팀 - 함께 훈련되지 않은 에이전트들로 구성된 팀 -가 다중 에이전트 작업을 수행하는 방법에 초점을 맞추고 있습니다.
$`N`$ 크기의 팀이 $`i`$ 개의 에이전트 $`a`$, 각각 정책 $\pi_a$를 실행하고, 나머지 $`j = N - i`$개의 에이전트가 정책 $\pi_b$을 실행하는 경우를 고려해봅시다. 팀의 공동 정책은 $\pi_{(a, i), (b, j)}$로 표현되며, 이에 따른 기대 할인 보상(expected discounted reward)은 다음과 같이 계산됩니다:
R = \mathbb E[\sum_t \gamma^t r_t]
혼합 팀의 성능을 측정하기 위해, 우리는 각각의 에이전트가 서로 다른 정책을 가질 수 있음을 고려합니다. $`i`$ 개의 에이전트 $`a`$, 각각 정책 $\pi_a$를 실행하고, 나머지 $`j = N - i`$개의 에이전트가 정책 $\pi_b$을 실행하는 경우를 고려해봅시다. 팀의 공동 정책은 $\pi_{(a, i), (b, j)}$로 표현되며, 이에 따른 기대 할인 보상(expected discounted reward)은 다음과 같이 계산됩니다:
R = \mathbb E[\sum_t \gamma^t r_t]
혼합 팀의 성능을 측정하기 위해, 우리는 각각의 에이전트가 서로 다른 정책을 가질 수 있음을 고려합니다.
이 글은 ArXiv의 공개 자료를 바탕으로 AI가 자동 번역 및 요약한 내용입니다.
저작권은 원저자에게 있으며, 인류 지식 발전에 기여한 연구자분들께 감사드립니다.