피드백 선형화 가능한 시스템을 위한 암시적 트라젝토리 계획 시간 변동 최적화 접근법

📝 원문 정보

- Title: Implicit Trajectory Planning for Feedback Linearizable Systems A Time-varying Optimization Approach
- ArXiv ID: 1910.00678
- 발행일: 2020-03-17
- 저자: Tianqi Zheng, John Simpson-Porco, Enrique Mallada

📝 초록

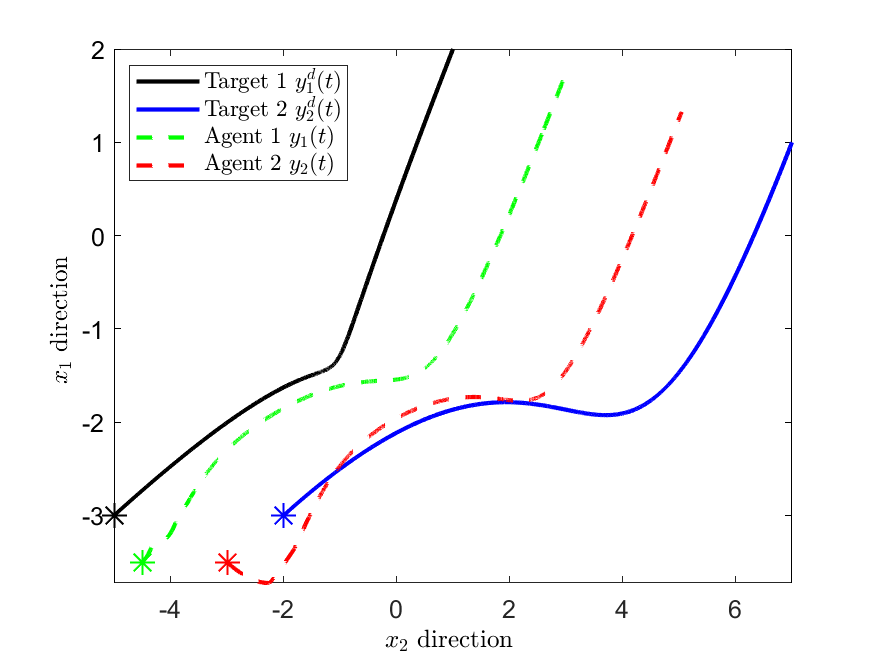
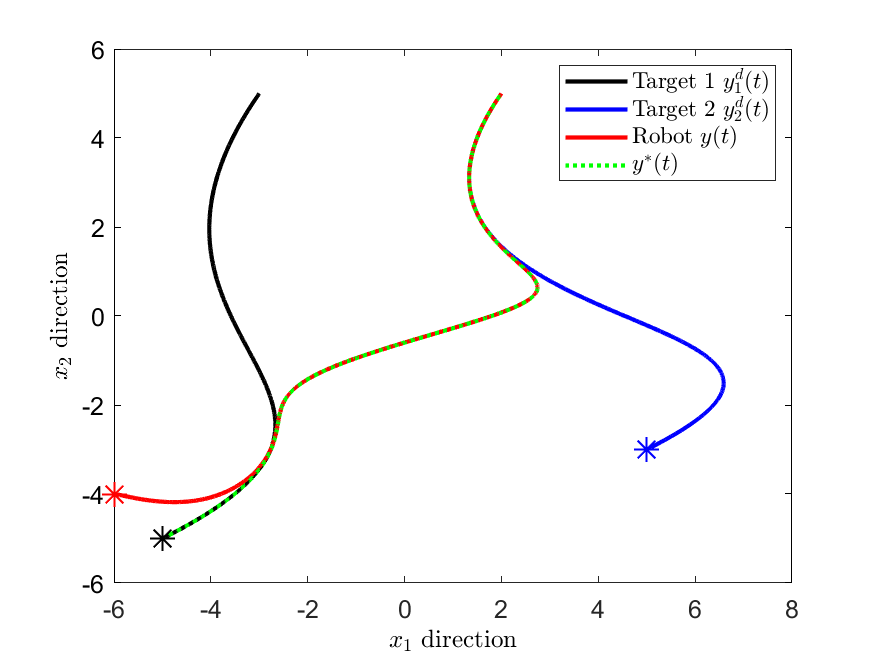
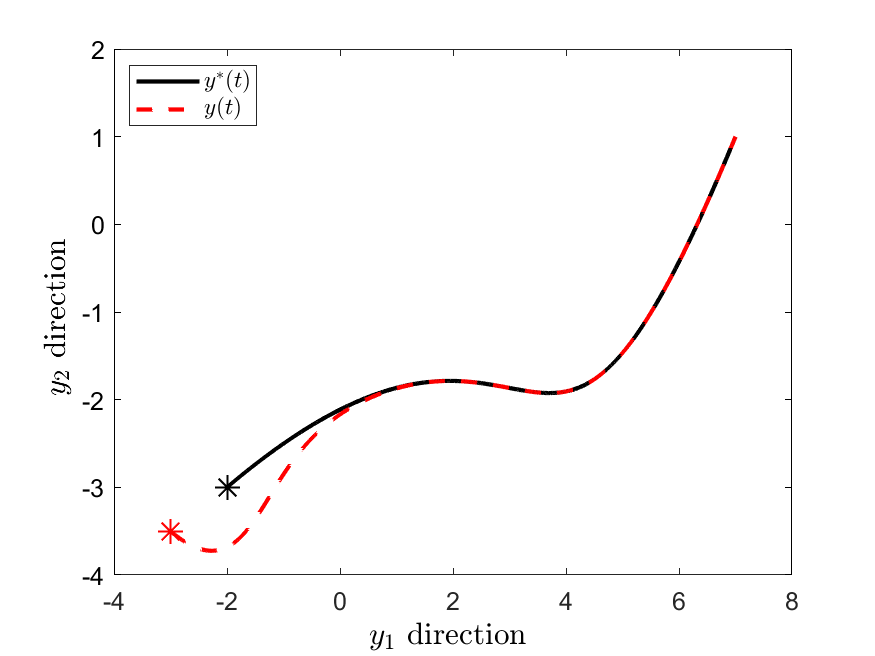
우리는 피드백 선형화 가능한 시스템의 실시간 경로 계획과 피드백 제어를 위한 최적화 기반 프레임워크를 개발했습니다. 이를 달성하기 위해, 목표 경로를 시간 변동 최적화 문제의 최적 해로 정의합니다. 그러나 일반적으로 이러한 경로는 비홀놈 제약 조건으로 인해 적절하지 않을 수 있습니다. 이 문제를 해결하기 위해, 목표 경로에 점근적으로 수렴하는 타당한 경로를 생성하는 제어 법칙을 설계했습니다. 구체적으로, 동적 전체 상태 선형화가 가능한 시스템의 경우, 제안된 제어 법칙은 비선형 시스템을 충분히 높은 차수의 최적화 알고리즘으로 암묵적으로 변환합니다. 우리는 최적화 알고리즘과 원래 시스템 모두에서 목표 경로에 대한 전역 지수 수렴성을 증명했습니다. 제약 조건이 있는 다중 대상 또는 다중 에이전트 추적 문제에서 우리의 방법의 효과를 설명합니다.

💡 논문 해설

- **핵심 요약**: 이 논문은 피드백 선형화 가능한 시스템에 대한 실시간 경로 계획 및 제어를 위한 최적화 기반 프레임워크를 개발하고 있습니다. 이를 위해 시간 변동 최적화 문제의 해를 목표 경로로 정의하며, 비홀놈 제약 조건이 있는 경우에도 타당한 경로를 생성할 수 있는 제어 법칙을 설계했습니다. - **문제 제기**: 이 연구는 피드백 선형화 가능한 시스템에서 실시간으로 경로 계획과 제어를 동시에 수행하려고 합니다. 그러나 이러한 시스템은 비홀놈 제약 조건 때문에 원하는 경로를 직접 추적할 수 없을 때가 있습니다. - **해결 방안 (핵심 기술)**: 이 논문에서는 시간 변동 최적화 문제의 해를 목표 경로로 설정하고, 이를 달성하기 위해 비선형 시스템을 고차수 최적화 알고리즘으로 변환하는 제어 법칙을 설계했습니다. 이 방법은 원래 시스템이 동적으로 전체 상태 선형화가 가능할 때 효과적입니다. - **주요 성과**: 논문에서는 제안된 방법을 통해 경로 계획 및 제어를 동시에 수행하면서, 비홀놈 제약 조건 하에서의 타당한 경로 추적이 가능함을 보였습니다. 또한, 최적화 알고리즘과 원래 시스템 모두에서 목표 경로에 대한 전역 지수 수렴성을 증명했습니다. - **의의 및 활용**: 이러한 접근법은 복잡한 제약 조건 하에서도 실시간으로 경로를 계획하고 제어할 수 있는 방법을 제공함으로써, 자율 주행 차량이나 로봇과 같은 다양한 분야에서 중요한 역할을 할 것입니다. 특히, 다중 대상 추적 문제와 같은 상황에서는 더욱 효과적일 것으로 예상됩니다.

📄 논문 발췌 (ArXiv Source)

📊 논문 시각자료 (Figures)

감사의 말씀

이 글의 저작권은 연구하신 과학자분들께 있으며, 인류 문명 발전에 공헌해주신 노고에 감사를 드립니다.