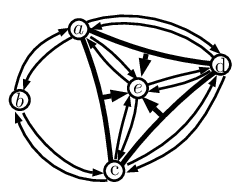
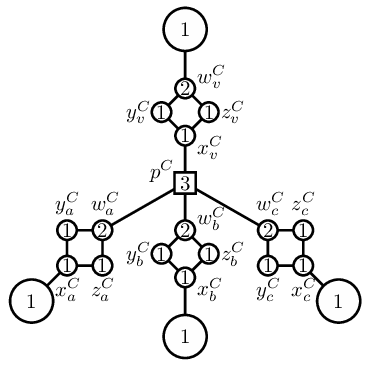
키에 대한 중요한 규칙 함수

📝 원문 정보

• Title: Unique key Horn functions
• ArXiv ID: 2002.06964
• 발행일: 2020-02-18
• 저자: Kristof Berczi, Endre Boros, Ondv{r}ej v{C}epek, Petr Kuv{c}era, Kazuhisa Makino

📝 초록 (Abstract)

관계형 데이터베이스가 주어졌을 때, 키는 해당 집합의 값 할당이 모든 다른 속성의 값을 고유하게 결정하는 속성들의 집합입니다. 데이터베이스는 함수적 종속성을 나타내는 순수한 호른 함수 $h$를 고유하게 정의합니다. 속성값들에 대한 지식이 집합 $A$에서 속성 $v$의 값을 결정하면, $A\rightarrow v$는 $h$의 함축입니다. 데이터베이스의 키가 $K$라면, 모든 속성 $v$에 대해 $K\rightarrow v$는 $h$의 함축입니다. 작은 크기의 키들은 다양한 문제에서 중요한 역할을 합니다. 본 연구에서는 순수한 호른 함수의 최소 키 집합에 대한 구조적 및 복잡도 결과를 제시합니다. 또한, 주어진 하이퍼그래프가 최소 키 세트로 나타나는 고유한 순수한 호른 함수가 존재하는 스페르너 하이퍼그래프를 특성화합니다. 더욱이, 이러한 하이퍼그래프를 인식하는 것이 이미 모든 하이페지의 크기가 두 개인 경우에도 co-NP-완전함을 보입니다. 긍정적인 측면에서는 인식 문제를 다항 시간에 결정할 수 있는 여러 그래프 클래스를 식별합니다. 또한, 최소 키들을 다항 지연으로 생성하는 알고리즘을 제시합니다. 키와 목표 집합 사이의 연결성을 확립함으로써 이 접근법은 임계값이 상수로 제한되는 경우 모든 최소 목표 집합을 다항 지연으로 생성할 수 있습니다. 증명에서 보듯이, 최소 키 문제는 임계값이 제한된 최소 목표 집합 선택 문제보다 적어도 같은 난이도입니다.

💡 논문 핵심 해설 (Deep Analysis)

This paper explores the connection between relational databases and pure Horn functions, focusing on keys with small sizes. It presents structural and complexity results for minimal key sets of these functions. A critical aspect is characterizing Sperner hypergraphs where there exists a unique pure Horn function representing the set of minimal keys. The research also shows that recognizing such hypergraphs is co-NP-complete even when every hyperedge has size two, but identifies polynomial-time solutions for specific graph classes.

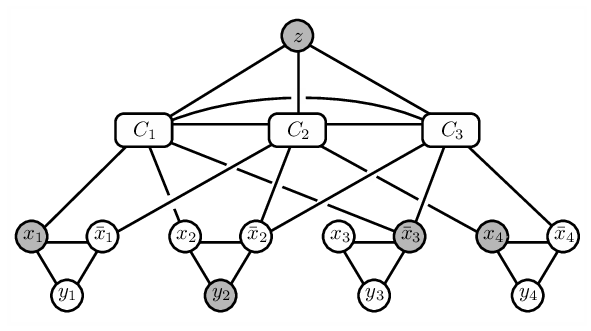
The significance lies in improving our understanding and practical handling of key sets within databases, which are crucial for efficient data access and management. This work not only advances theoretical knowledge but also offers practical algorithms that can be applied to real-world problems involving database optimization and security.

📄 논문 본문 발췌 (Translation)

📸 추가 이미지 갤러리

Reference