이종 라우팅 게임에서 사용자 균형의 안정성에 관하여
📝 원문 정보
- Title: On stability of users equilibria in heterogeneous routing games- ArXiv ID: 1912.02007
- 발행일: 2019-12-05
- 저자: Leonardo Cianfanelli and Giacomo Como
📝 초록
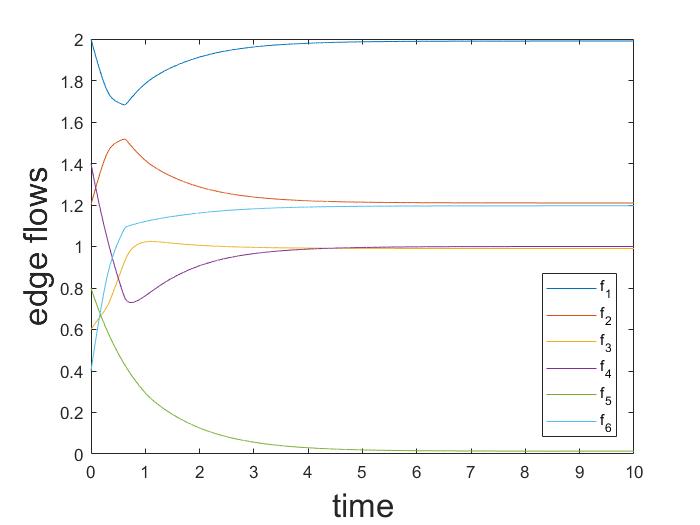
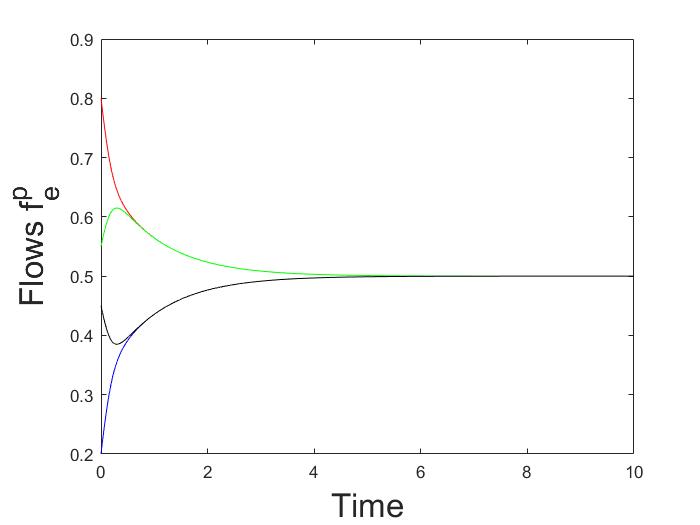
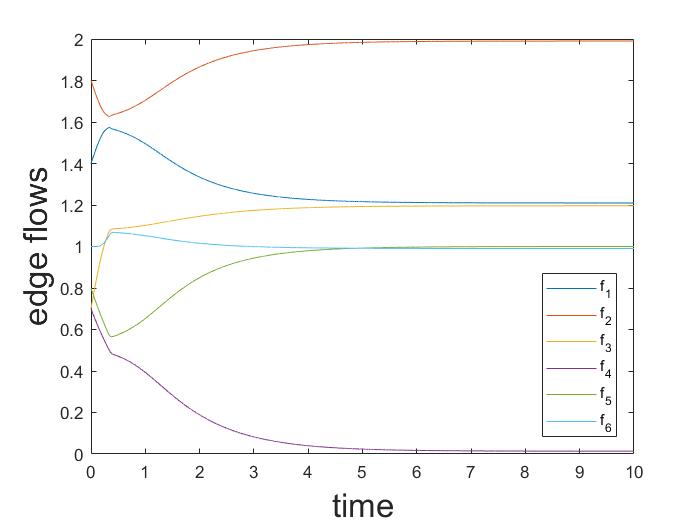
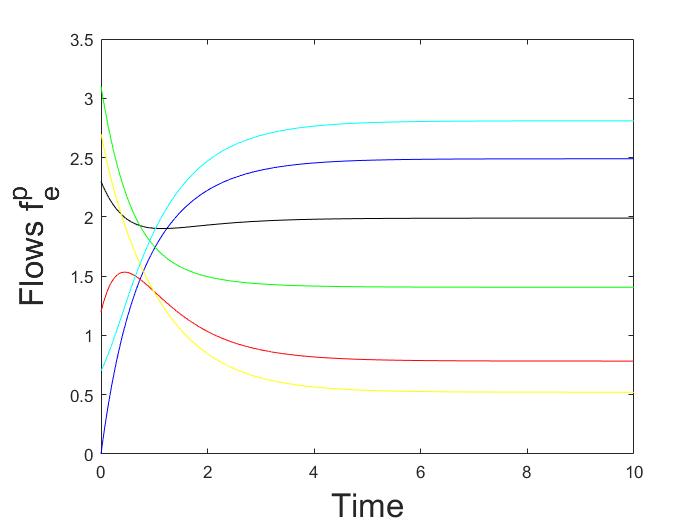
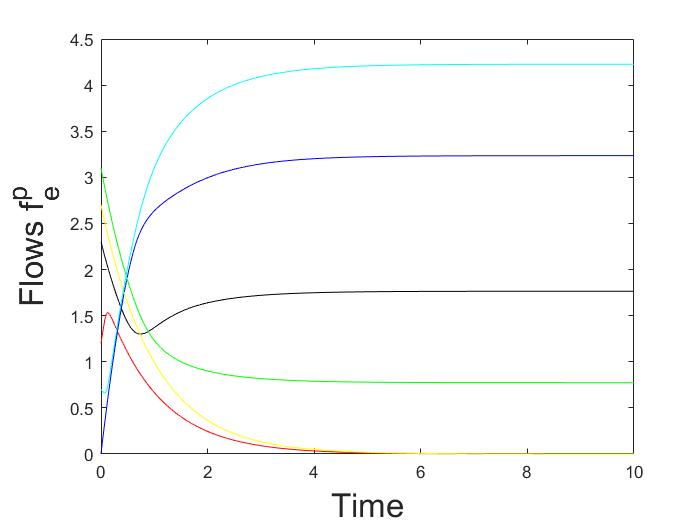
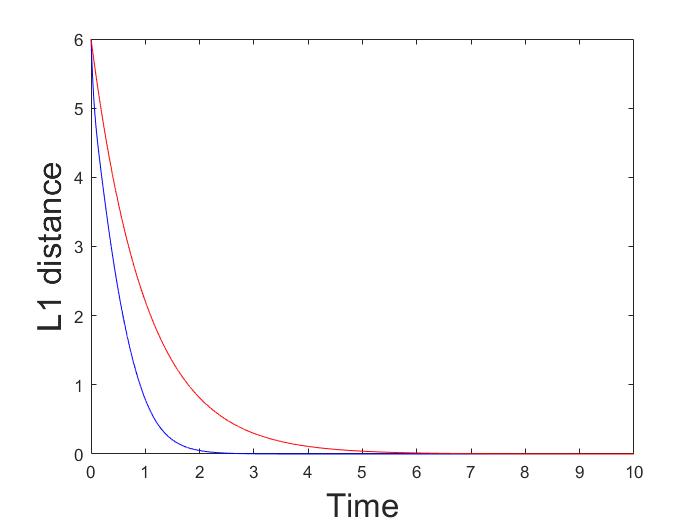
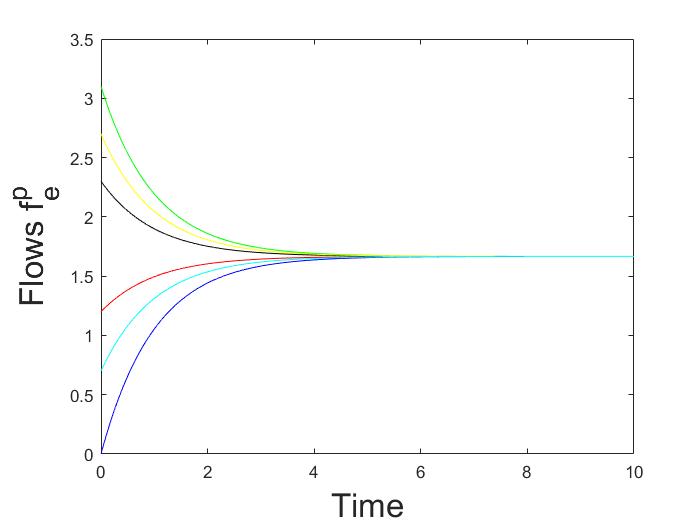
이 연구에서는 이질적인 경로 게임에서 결정론적 로짓 동역학의 근사적 행동을 분석한다. 특히, 병렬 경로가 있는 방향 다중 그래프와 그러한 다중 그래프의 직렬 조합에서 동역학은 전역적으로 점근적으로 안정된 고정점을 갖는다는 것을 증명하였다. 또한, 노이즈가 사라질 때 동역학의 유일한 고정점은 Wardrop 균형 집합에 접근한다. 이 결과는 동역학의 총 흐름이 단조성과 그 제이코비안(Jacobian)이 열(column)에 대해 엄격하게 대각 우세(diagonally dominant)라는 사실을 기반으로 한다.💡 논문 해설
**핵심 요약**: 이 논문은 복잡한 네트워크 시스템에서 사용자가 선택하는 경로가 어떻게 안정적으로 균형 상태에 도달하는지 분석한다. 특히, 여러 경로 중 하나를 선택해야 하는 상황에서 이러한 동역학적 프로세스가 어떻게 작동하고 어떤 결과를 가져오는지를 설명한다.문제 제기: 네트워크 사용자가 다양한 경로를 선택할 때, 각 사용자는 최소한의 비용이나 시간을 추구하며 이 과정에서 경로 선택이 어떻게 안정적인 균형 상태에 도달하는지 이해하기 어렵다. 이러한 문제는 특히 복잡하고 여러 경로가 있는 네트워크에서 중요하다.
해결 방안 (핵심 기술): 논문은 결정론적 로짓 동역학을 사용하여 이러한 문제를 해결한다. 이 모델에서는 각 사용자가 특정 경로를 선택할 확률이 그 경로의 비용에 따라 변하게 된다. 연구진은 이러한 동역학이 병렬 경로가 있는 방향 다중 그래프와 그러한 그래프들의 직렬 조합에서 전역적으로 점근적으로 안정된 고정점을 갖는다는 것을 증명하였다.
주요 성과: 논문은 이동 경로 선택 동역학의 고정점이 Wardrop 균형 상태에 접근한다는 것을 입증하였으며, 특히 노이즈가 줄어들 때 더욱 그러하다. 이를 통해 복잡한 네트워크에서 사용자들이 어떻게 최적의 경로를 선택할 수 있는지 이해할 수 있게 된다.
의의 및 활용: 이 연구는 실생활에서 복잡한 네트워크 시스템을 설계하고 관리하는 데 큰 도움이 될 수 있다. 예를 들어, 교통 체증 문제 해결이나 인터넷 트래픽 최적화 등 다양한 분야에서 적용 가능하다.
📄 논문 발췌 (ArXiv Source)
📊 논문 시각자료 (Figures)