데이터 생성 속도가 분석 능력을 초월하고 있습니다. 데이터베이스 커뮤니티는 근사 질의 처리(AQP) 기법을 개척해 정확한 결과를 계산하는 데 필요한 시간의 일부만으로 근사 결과를 제공할 수 있게 했습니다. 본 연구에서는 딥러닝(DL)을 활용하여 데이터 탐색 및 시각화와 같은 상호작용적인 응용 프로그램에서 집합 질의에 대답하는 방법을 탐구했습니다. 우리는 무감독 학습 기반 접근법인 딥 생성 모델을 사용해 데이터 분포를 충실하게 학습하여, 학습된 모델로부터 샘플을 생성함으로써 근사적으로 집합 질의에 대답할 수 있습니다. 이 모델은 종종 컴팩트한 크기(수백 KB)로 이루어져 있어 임의의 AQP 질의를 데이터베이스 서버와 통신하지 않고 클라이언트 측에서 처리할 수 있습니다. 또한, 우리는 모델 편향을 식별하고 이를 거부 샘플링 기반 접근법과 AQP를 위한 모델 연합 알고리즘을 통해 최소화하는 데 중점을 두었습니다. 우리의 광범위한 실험 결과는 제안된 접근법이 높은 정확도와 낮은 대기 시간으로 답변을 제공할 수 있음을 보여줍니다.
**핵심 요약**: 이 논문에서는 딥러닝을 이용해 데이터 분석 속도를 빠르게 하는 방법을 제시합니다. 특히, 집합 질의에 대한 근사 답변을 제공하는 새로운 접근법을 소개하며, 이를 통해 클라이언트 측에서 데이터베이스 서버와 통신 없이 임의의 질의를 처리할 수 있습니다.
**배경**
이 섹션에서는 생성 모델과 특히 가변 오토인코더(VAE)에 대한 기본적인 배경을 제공합니다.
주어진 데이터 포인트 집합 $`X=\{x_1, \ldots, x_n\}`$가 있다고 가정하면, 이들은 어떤 알려지지 않은 확률 분포 $`P(X)`$에 따라 분포되어 있습니다. 생성 모델은 이러한 분포를 학습하고, 가능한 한 유사한 근사 확률 분포 $`Q`$를 추구합니다. 대부분의 생성 모델은 또한 이 모델로부터 샘플을 생성할 수 있으며, 이런 경우 $`X'=\{x'_1, \ldots\}`$는 $`X`$와 유사한 통계적 속성을 갖습니다.
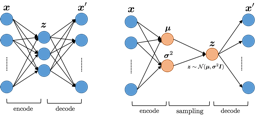
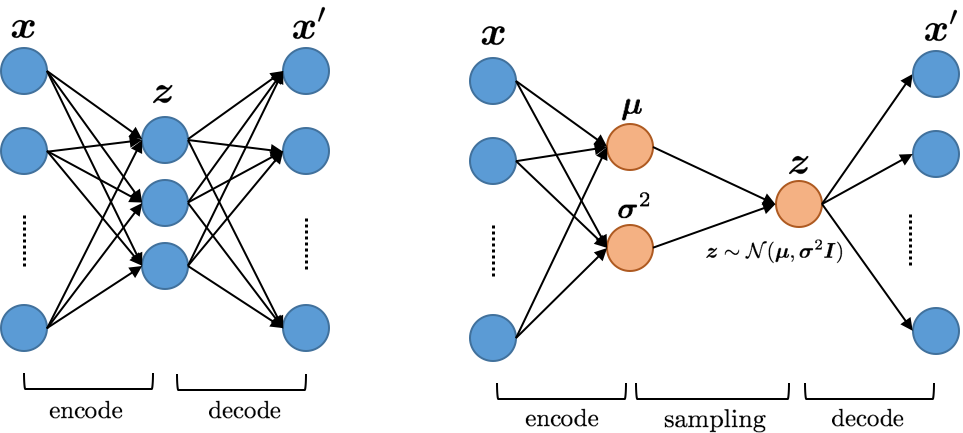
딥 생성 모델은 강력한 함수 근사기(주로 딥 신경망)를 사용하여 분포를 근사화하는 데 사용됩니다. VAE는 다양한 복잡한 데이터 분포를 모델링하고 샘플을 생성할 수 있는 생성 모델의 한 종류입니다. 이들은 훈련이 매우 효율적이며, 이미지, 텍스트 및 음악 등 다양한 도메인에 효과적으로 적용될 수 있습니다.
잠재 변수는 데이터 특성을 포착하는 중간 표현으로 사용됩니다. $`X`$가 모델링하려는 관계적 데이터이고, $`z`$가 잠재 변수라고 가정하면, $`P(X|z)`$는 주어진 잠재 변수로부터 데이터를 생성하는 분포입니다. $`P(X) = \int P(X|z)P(z)dz`$로 표현되는 관계에서 $`z`$는 결합 확률 $`P(X,z)`$에서 제거됩니다.
VAE의 핵심 아이디어는 $`P(z|X)`$를 추론하는 것입니다. 이를 위해 우리는 변형 추론(VI) 방법을 사용합니다. VI의 주요 아이디어는 추론을 최적화 문제로 접근하는 것입니다. 진정한 분포 $`P(z|X)`$를 평가하기 쉬운 간단한 분포(예: 가우시안)인 $`Q`$로 모델링하고, KL 발산 메트릭을 사용하여 두 분포 사이의 차이를 최소화합니다. 이는 $`P`$와 $`Q`$가 얼마나 다른지를 알려줍니다.
$$
\begin{equation}
\begin{split}
D_{KL}[Q(z|X)||P(z|X)] = \sum_{z} Q(z|X) \log(\frac{Q(z|X)}{P(z|X)}) = \\
E[\log(\frac{Q(z|X)}{P(z|X)})] = E[\log(Q(z|X)) - \log(P(z|X))]
\end{split}
\end{equation}
$$
이를 통해 $`Q(z|X)`$와 $`P(X|z)`$는 잠재 공간으로의 데이터 프로젝션과 주어진 잠재 변수 $`z`$로부터 데이터를 생성하는 관계입니다.
VAE를 이용한 AQP
이 섹션에서는 VAE를 사용하여 AQP에 대한 두 단계 접근법을 제공합니다. 이는 입력 인코딩 및 모델 편향으로 인한 근사 오류 등 여러 이론적이고 실용적인 문제를 해결해야 합니다.
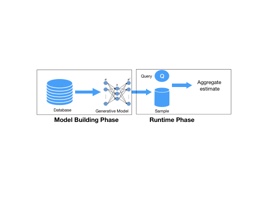
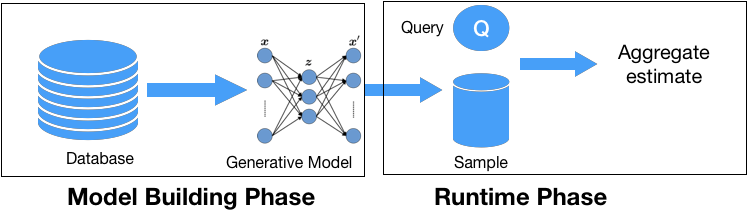
제안된 접근법은 두 단계로 진행됩니다: 모델 구축 단계에서는 데이터셋 $`R`$에 대해 딥 생성 모델 $`M_R`$을 학습합니다. 이렇게 함으로써 기본 데이터 분포를 학습할 수 있습니다. 이 단계에서는 전체 데이터셋에 대한 단일 모델이 구성됩니다(Section 13에서 제한을 완화). 모델이 훈련되면, 이를 데이터셋의 요약 표현으로 사용할 수 있습니다. 실행 시 단계에서는 AQP 시스템이 DL 모델을 사용하여 기저 분포로부터 샘플 $`S`$를 생성합니다. 주어진 질의는 $`S`$에 대해 재작성되어 실행됩니다.
VAE는 관계적 데이터에서 어떻게 훈련되고 AQP에 활용되는지 설명합니다.
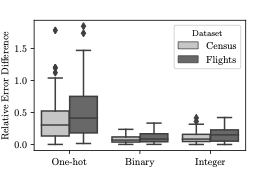
관계는 종종 이산형 또는 연속형 혼합 데이터 타입을 포함하며, 이미지와 텍스트와 같은 동질 도메인과 달리 다양한 특성을 가집니다. 첫 번째 단계는 각 튜플 $`t`$를 차원 $`d`$의 벡터로 표현하는 것입니다. 설명을 간단히 하기 위해, 이하에서는 one-hot 인코딩에 대해 설명하고 Section 7.5에서 효과적인 다른 인코딩 방법을 다룹니다.
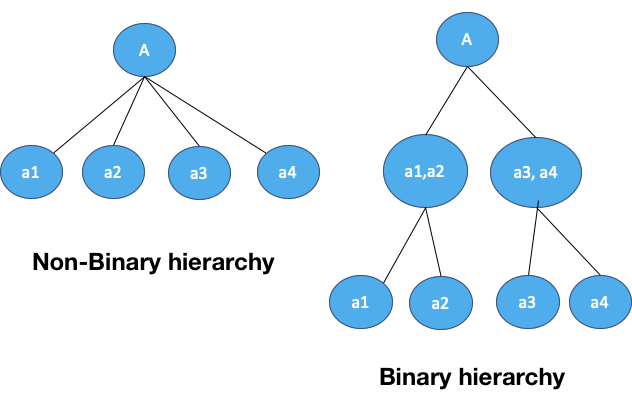
one-hot 인코딩은 각 튜플을 $`d = \sum_{i=1}^{m}|Dom(A_i)|`$ 차원의 벡터로 표현합니다. 이 중 주어진 도메인 값에 해당하는 위치가 1로 설정됩니다. 예를 들어, 두 개의 이진 속성 $`A_1`$, $`A_2`$을 가진 관계 $`R`$의 튜플은 4차원 이진 벡터로 표현될 수 있습니다. $`A_1=0`, $A_2=1$인 튜플은 $[1, 0, 0, 1]$, $A_1=1, $`A_2=1`$인 튜플은 $`[0, 1, 0, 1]`$으로 표현됩니다. 이 방법은 작은 속성 도메인에 대해 효율적이지만, 관계가 수백만 개의 고유 값을 가질 경우 번거로울 수 있습니다.
모든 튜플이 적절하게 인코딩되면 VAE를 사용하여 기본 분포를 학습할 수 있습니다. 입력 및 잠재 차원의 크기를 각각 $`d`$와 $`d'`$라고 합니다. one-hot 인코딩을 사용하면 $`d=\sum_{i=1}^{m}|Dom(A_i)|`$. $`d'`$가 증가함에 따라 분포를 더 정확하게 학습할 수 있지만, 모델 크기가 커집니다. 모델이 훈련되면 이를 사용하여 샘플 $`X'`$을 생성할 수 있습니다.
생성된 튜플은 다음과 같이 생성됩니다: 잠재 공간에서 샘플을 생성하고 디코더 네트워크를 적용하여 잠재 공간의 점을 튜플로 변환합니다. Section 6에 설명했듯이, 잠재 공간은 종종 표준 정규 분포와 같이 샘플링하기 쉬운 확률 분포입니다.
근사 오류 처리
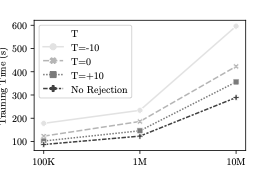
이 섹션에서는 모델 편향으로 인한 근사 오류를 고려하고 이를 완화하는 효과적인 거부 샘플링을 제안합니다.
샘플에 대한 집합 추정은 전체 데이터셋에 대해 계산된 정확한 결과와 차이가 있을 수 있으며, 이 차이는 샘플링 오차라고 합니다. 기존 AQP 및 제안된 접근법 모두 이러한 오차를 겪습니다.
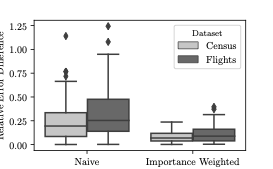
추출 오차는 또한 샘플이 기본 데이터셋을 대표하지 못할 때 발생하며, 이를 완화하기 위해 중요 가중치와 부트스트랩과 같은 다양한 방법들이 사용됩니다. 그러나 VAE에서 생성된 샘플은 근사 분포로부터 생성되므로 편향된 샘플이 될 수 있습니다.
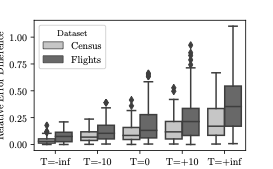
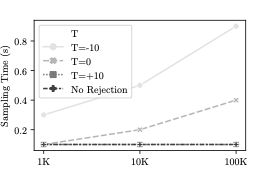
거부 샘플링은 이러한 문제를 해결할 수 있는 효과적인 접근법입니다. 이 접근법의 핵심 아이디어는 VAE 모델로부터 생성된 샘플 $`x`$를 원래 및 근사 확률 분포에서 각각 $`p(x)`$, $`q(x)`$ 확률로 받아들여, $`\frac{p(x)}{M \times q(x)}`$ 확률로 샘플을 수락하는 것입니다. 여기서 $`M`$은 모든 $`x`$에 대한 비율 $`p(x)/q(x)`$의 상한입니다.
이러한 접근법은 VAE 모델로부터 생성된 임의의 수의 샘플을 생성하고 거부 샘플링을 적용하여 정확하고 편향되지 않은 집합 추정을 생성할 수 있습니다. 이를 위해, $`p(x)`$ 값을 추정하는 것이 필요합니다. 이는 데이터셋에 접근하는 것이 매우 비효율적이므로 VAE 모델로부터 간접적으로 추정하는 방법이 더 좋습니다.