정확한 경계 기반 FEM을 이용한 전자기 분석 및 다 ölçek 구조물에의 응용
📝 원문 정보
- Title: An Accurate Edge-based FEM for Electromagnetic Analysis with Its Applications to Multiscale Structures- ArXiv ID: 1910.01850
- 발행일: 2019-10-30
- 저자: Yangfan Zhang, Pengfei Wang, Wenping Li, Shunchuan Yang
📝 초록
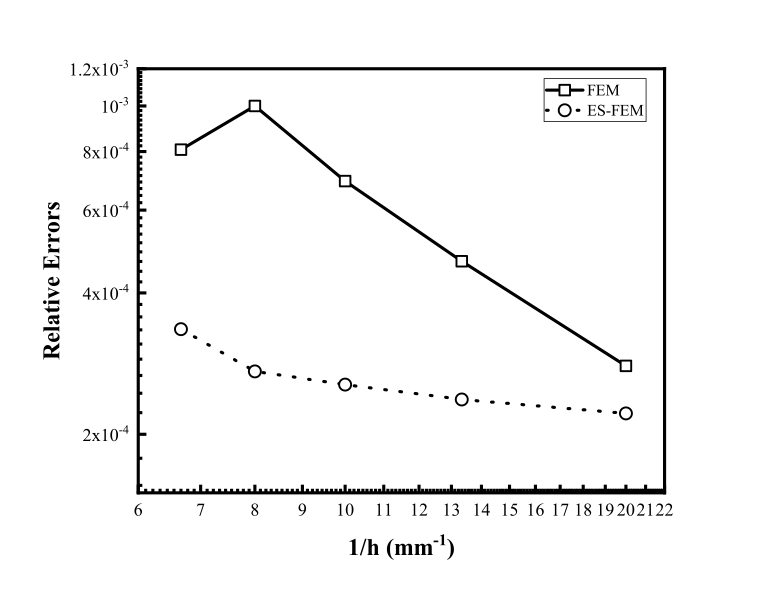
이 논문은 2차원 원통형과 3차원 카르테시안 시스템 모두에 대한 전자기 분석을 위한 정확한 변위 기반 부드러운 유한요소 방법(ES-FEM)을 소개한다. 이 방법은 전통적인 FEM에 비해 정확성과 수치 안정성이 향상되었으며, 메시 왜곡에도 거의 독립적이다. ES-FEM에서는 계산 도메인을 각 요소의 변별에 연결된 중복되지 않는 부드러운 도메인으로 나눈다. 이는 2차원 도메인에서 삼각형, 3차원 도메인에서는 사면체로 구분한다. 그런 다음, FEM의 강도 행렬에서 기울기 성분을 부드럽게 하기 위해 기울기 부드러움 기법(GST)을 사용한다. 정확성과 수치 안정성을 검증하기 위한 여러 수치 실험을 수행하였고, 결과는 ES-FEM이 훨씬 더 정확한 결과를 얻을 수 있으며 메시 왜곡에 거의 독립적임을 보여주었다.💡 논문 해설
**핵심 요약**: 이 논문은 전자기 분석을 위한 새로운 유한요소 방법인 ES-FEM(Edge-based Smoothed Finite Element Method)를 소개한다. 이 방법은 기존의 FEM(Finite Element Method)보다 더 정확하고 수치적으로 안정적이다.문제 제기: 전통적인 FEM는 메시 왜곡에 민감하여 분석의 정확성이 떨어질 수 있다. 따라서, 더욱 정밀한 계산과 안정성을 제공하는 새로운 방법이 필요하다.
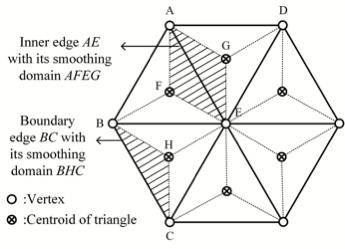
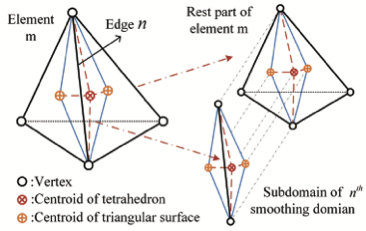
해결 방안 (핵심 기술): ES-FEM은 모든 요소 변별에 연결된 중복되지 않는 부드러운 도메인을 이용한다. 이는 2차원에서는 삼각형, 3차원에서는 사면체로 구성된다. 그런 다음 GST(Gradient Smoothing Technique)를 사용하여 FEM의 강도 행렬에서 기울기 성분을 부드럽게 한다. 이러한 방법은 계산 도메인을 더욱 정밀하게 나누고 각 부분에서 부드러움을 추가함으로써 계산의 정확성을 향상시킨다.
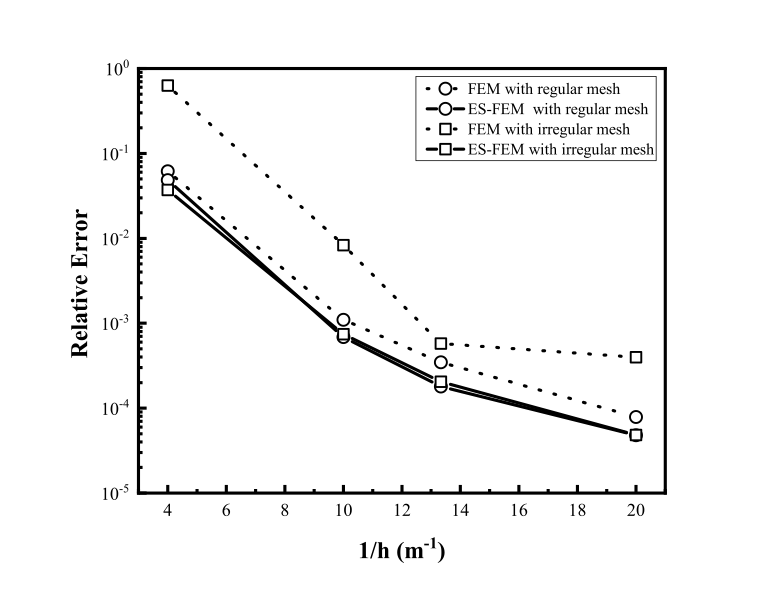
주요 성과: ES-FEM은 여러 수치 실험을 통해 더 정확한 결과를 얻는 것이 확인되었다. 또한, 메시 왜곡에 거의 독립적이어서 다양한 조건에서도 안정적인 계산이 가능하다.
의의 및 활용: 이 연구는 전자기 분석에서 보다 정밀하고 안정적인 계산을 제공하는 새로운 방법론을 제안한다. 이를 통해 엔지니어링과 과학 분야에서 더욱 정확한 시뮬레이션과 예측이 가능해진다.
📄 논문 발췌 (ArXiv Source)
📊 논문 시각자료 (Figures)