표면 그래프의 최소 자르기 알고리즘
📝 원문 정보
- Title: Minimum Cuts in Surface Graphs- ArXiv ID: 1910.04278
- 발행일: 2019-10-11
- 저자: Erin W. Chambers and Jeff Erickson and Kyle Fox and Amir Nayyeri
📝 초록
이 연구에서는 방향성이 있는 표면에 내장된 무방향 그래프에서 최소 $(s,t)$-컷과 전역 최소 컷을 효율적으로 계산하는 알고리즘을 설명합니다. $n$ 개의 정점으로 구성된 엣지 가중치가 주어진 무방향 그래프 $G$와 유한한 표면 $g$에 내장되어 있을 때, 우리의 알고리즘은 $g^{O(g)} n \log \log n$ 또는 $2^{O(g)} n \log n$ 시간 중 더 좋은 시간 복잡도로 이 문제를 해결할 수 있습니다. $g$가 상수일 경우, 우리의 $g^{O(g)} n \log \log n$ 시간 알고리즘은 계획 그래프에서 최소 컷을 계산하는 알려진 가장 빠른 실행 시간과 일치합니다. 최소 컷을 찾는 우리의 알고리즘은 주어진 $\mathbb{Z}_2$-동형류에 속한 하위 그래프의 최소 가중치를 찾는 문제로 축소되며, 이러한 후자의 문제에 대한 효율적인 알고리즘도 제공합니다. $G$가 $b$ 개의 경계 구성 요소를 갖는 표면 위에 내장되어 있을 때, 이 알고리즘들은 $(g + b)^{O(g + b)} n \log \log n$ 또는 $2^{O(g + b)} n \log n$ 시간 복잡도로 작동합니다. 또한 단일 입력 사이클과 동형인 하위 그래프의 최소 가중치를 찾는 것은 NP-완전 문제임을 증명하여 이러한 후자의 문제에 대해 지수적 의존성 $g$를 개선할 가능성은 적다고 보여줍니다.💡 논문 해설
**핵심 요약**: 이 연구에서는 표면이 내장된 그래프에서 최소 컷을 효율적으로 계산하는 알고리즘을 제시합니다. 특히, 이러한 그래프의 특성을 활용하여 빠른 시간 복잡도를 달성하고자 노력했습니다.문제 제기: 이 연구에서는 표면이 내장된 무방향 그래프에서 최소 컷을 효율적으로 찾는 방법을 모색합니다. 최소 컷은 그래프의 두 부분으로 나누어질 때, 가장 적은 양의 엣지 가중치를 갖는 경계입니다.
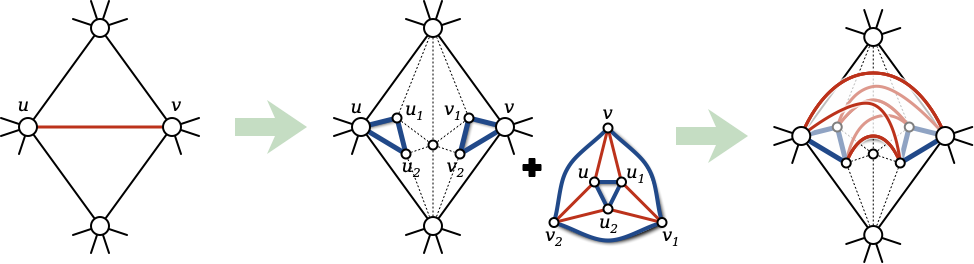
해결 방안 (핵심 기술): 연구진들은 주어진 $\mathbb{Z}_2$-동형류에 속한 하위 그래프에서 최소 가중치를 찾는 문제로 원래의 컷 계산 문제를 축소시키는 방법을 사용했습니다. 이 과정은 표면이 내장된 그래프의 특성을 활용하여 빠르게 해결할 수 있습니다. 예를 들어, 그래프가 평면 위에 있다면 $g^{O(g)} n \log \log n$ 시간 복잡도로 최적의 결과를 얻을 수 있습니다.
주요 성과: 연구진은 $2^{O(g)} n \log n$ 또는 $g^{O(g)} n \log \log n$ 시간 복잡도에서 최소 컷을 찾는 알고리즘을 제안했습니다. 이 결과는 특히 표면이 단순한 경우, 즉 $g$가 상수인 경우에는 계획 그래프의 알고리즘과 동일한 효율성을 보여줍니다.
의의 및 활용: 이러한 연구는 복잡한 그래프 구조에서 최적의 경로를 찾는 문제를 해결하는 데 유용합니다. 예를 들어, 통신 네트워크나 도시 교통 시스템과 같은 실제 시스템에서 효율적인 경로 계획을 위해서는 최소 컷 알고리즘이 필수적입니다.
📄 논문 발췌 (ArXiv Source)
📊 논문 시각자료 (Figures)