통계적 강건한 중국인 나머지 정리 다수의 수에 대한 적용
📝 원문 정보
- Title: Statistical Robust Chinese Remainder Theorem for Multiple Numbers- ArXiv ID: 1909.00225
- 발행일: 2019-09-04
- 저자: Hanshen Xiao, Nan Du, Zhikang T. Wang and Guoqiang Xiao
📝 초록
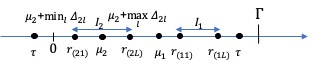
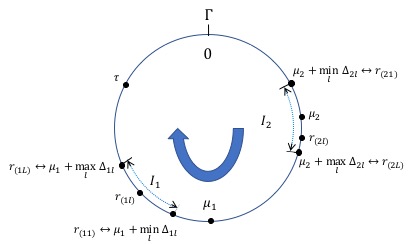
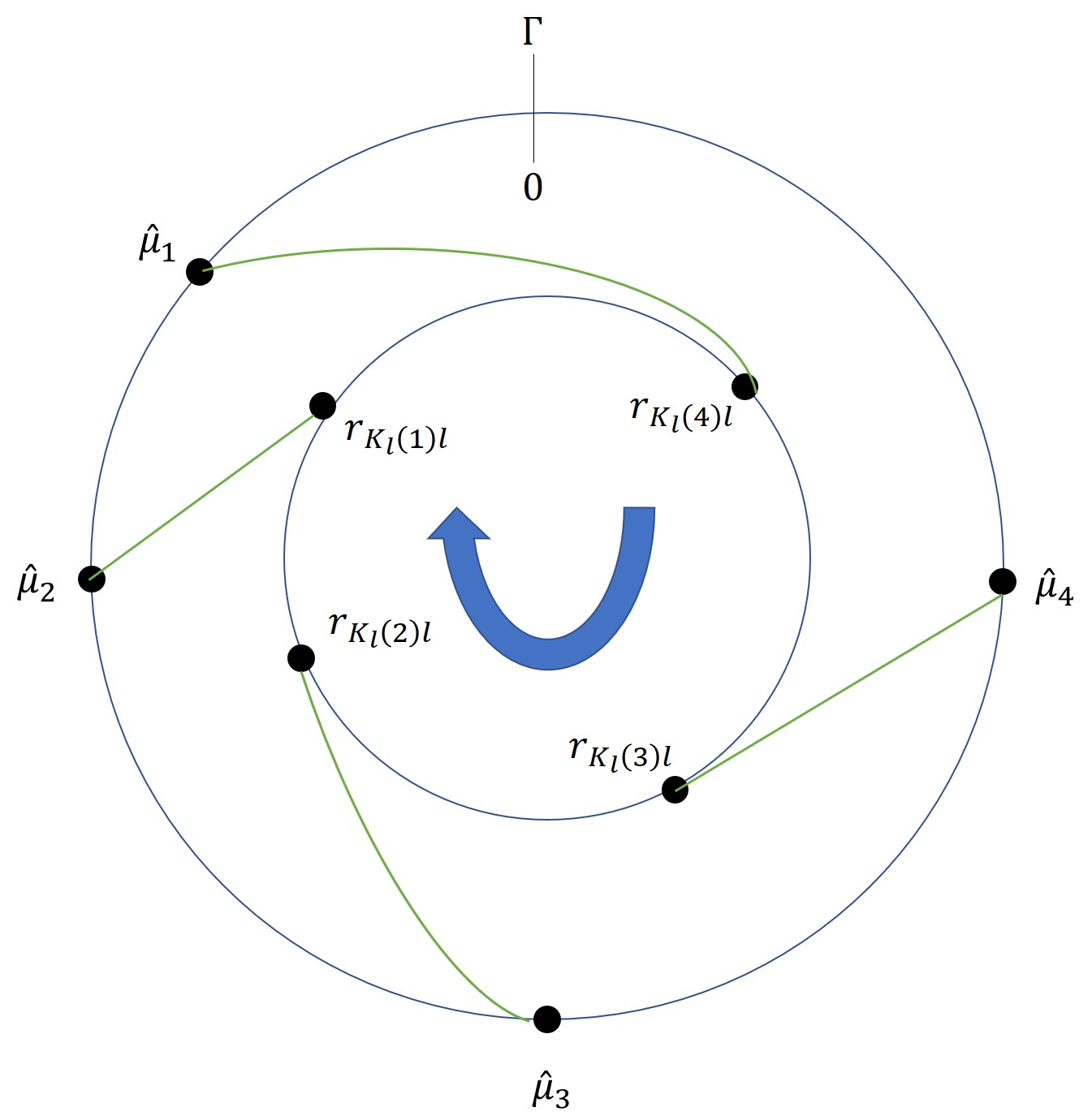
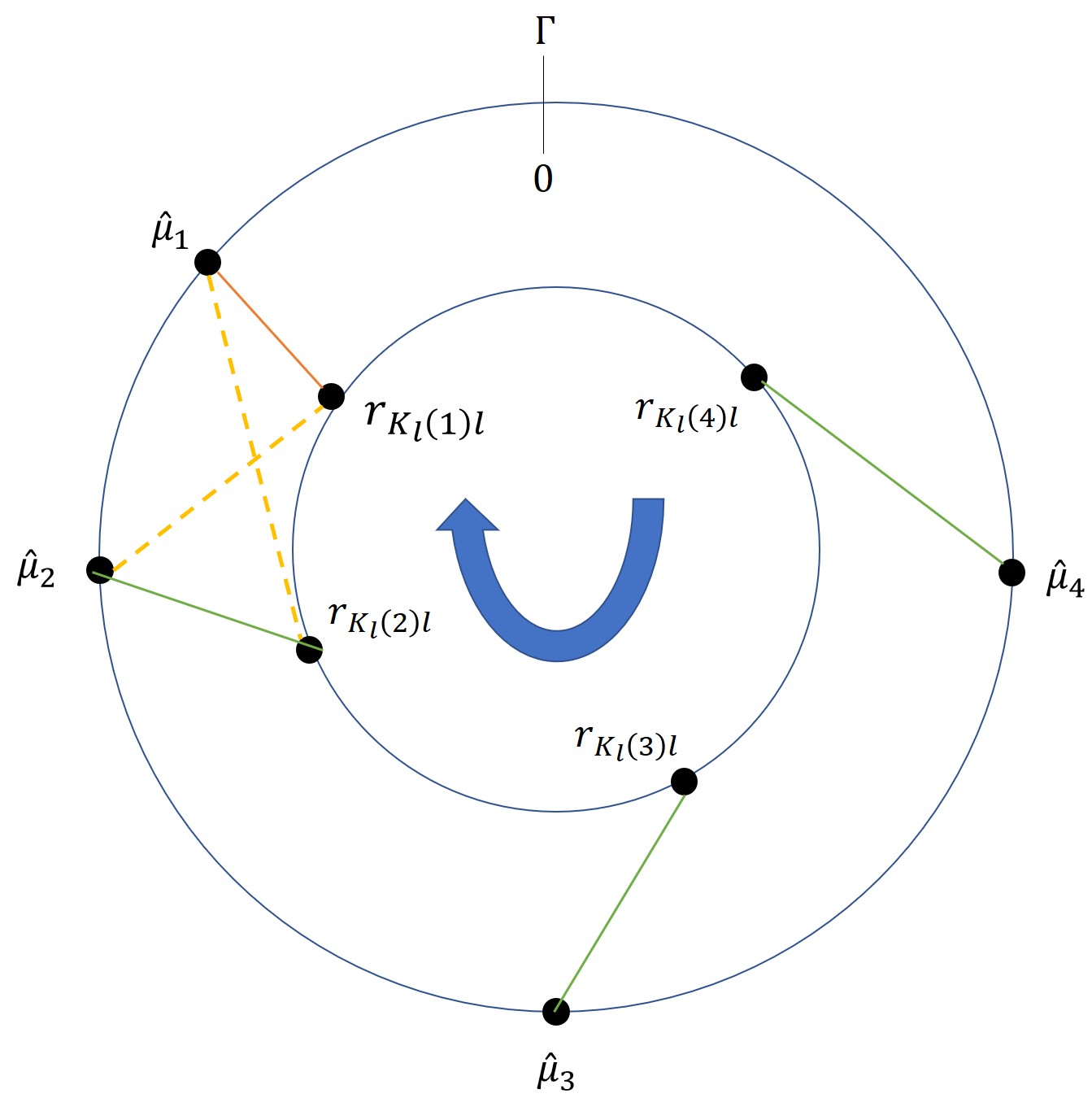
일반화된 중국인의 나머지 정리(CRT)는 모호성 해석과 관련된 문제를 해결하기 위한 잘 알려진 접근법이다. 본 논문에서는 통계학적 관점에서 여러 개의 수에 대한 CRT 기반 복원을 강건하게 하는 방법을 연구하였다. 이 글은 CRT 기반 다중 매개변수 추정의 기본적인 통계 모델에 대한 첫 번째 엄밀한 분석이라고 할 수 있다. 이를 해결하기 위해 두 가지 새로운 접근법이 제시되었다. 하나는 잔차 클러스터링에 대한 조건부 최대 사후 확률(MAP) 추정을 직접 계산하는 것이고, 다른 하나는 일반화된 감싸인 가우시안 혼합 모델을 이용해 MAP를 반복적으로 찾는 것이다. 또한 강건성을 향상시키기 위해 잔차 오류 정정 코드가 도입되었다. 실험 결과는 통계적 방식이 특히 높은 노이즈 상황에서 기존의 결정론적 접근법보다 훨씬 더 강건한 성능을 보였음을 나타냈다.💡 논문 해설
**핵심 요약**: 본 논문은 CRT(중국인의 나머지 정리)를 이용해 여러 수를 복원하는 방법에 대한 통계적 접근법을 제시하고 있다. 이는 기존 방법보다 강건성을 높이는 새로운 방식을 제안하며, 특히 노이즈가 많은 상황에서 더욱 효과적이다.문제 제기: CRT는 두 개 이상의 수를 복원하는 문제에 있어서 모호성 해소와 관련된 여러 문제를 해결하기 위한 중요한 도구로 사용된다. 그러나 기존 방법들은 높은 노이즈 상황에서 성능이 저하되는 문제가 있다.
해결 방안 (핵심 기술): 연구진은 CRT를 이용한 복원 과정을 통계학적 모델링을 통해 강건하게 만들었다. 이 방법에는 두 가지 주요 접근법이 포함된다.
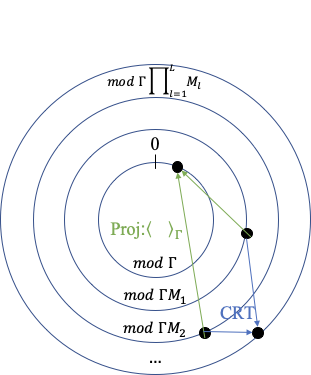
- MAP 추정: 잔차 클러스터링에 대한 조건부 최대 사후 확률(MAP) 추정을 직접 계산하는 것이다. 이를 통해 잔차가 어떤 그룹으로 묶여 있는지를 결정한다.
- 감싸인 가우시안 혼합 모델: 일반화된 감싸인 가우시안 혼합 모델을 이용해 MAP를 반복적으로 찾는다. 이 방법은 복잡한 분포를 다루는데 효과적이다.
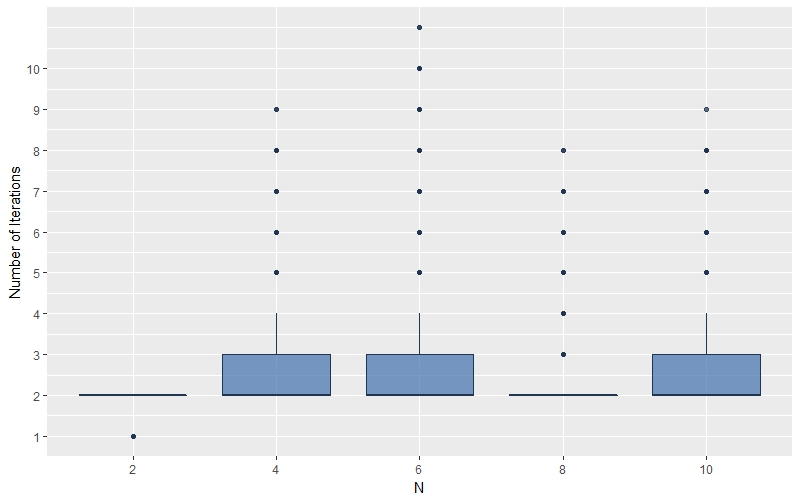
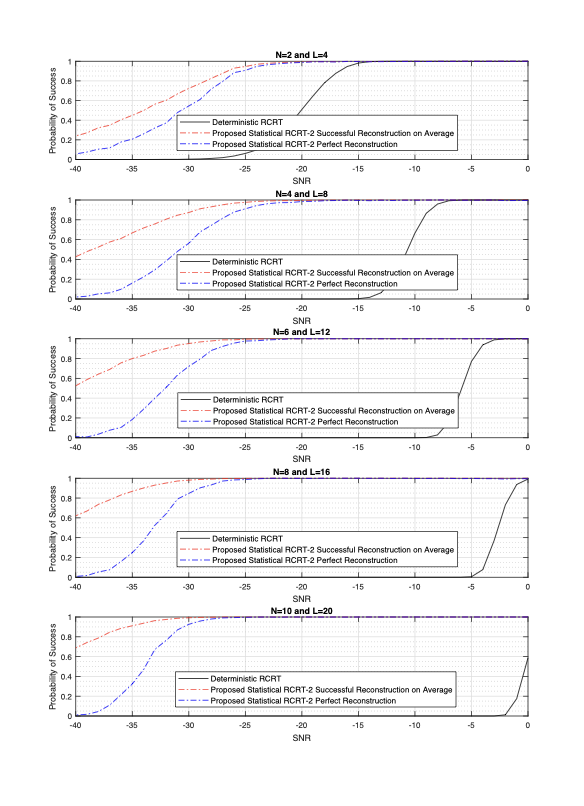
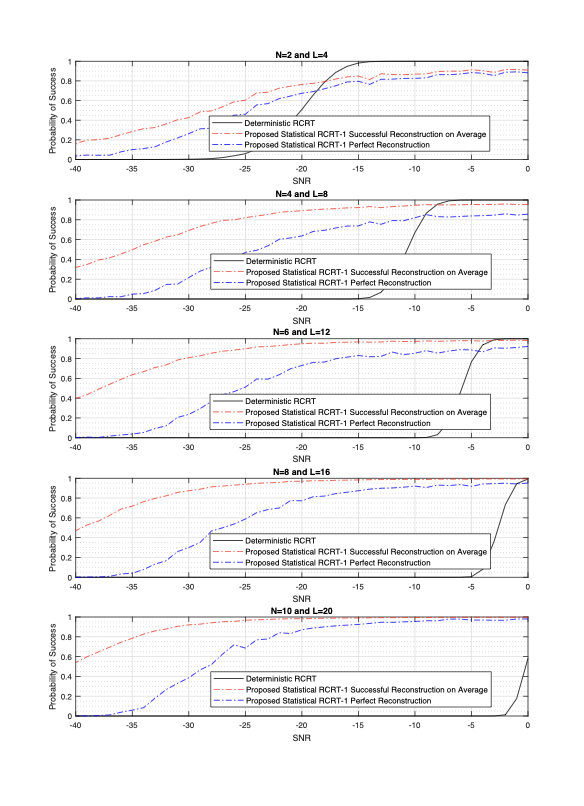
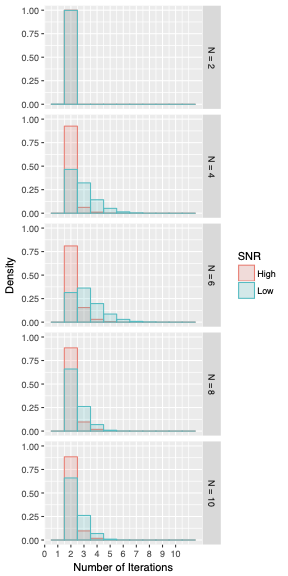
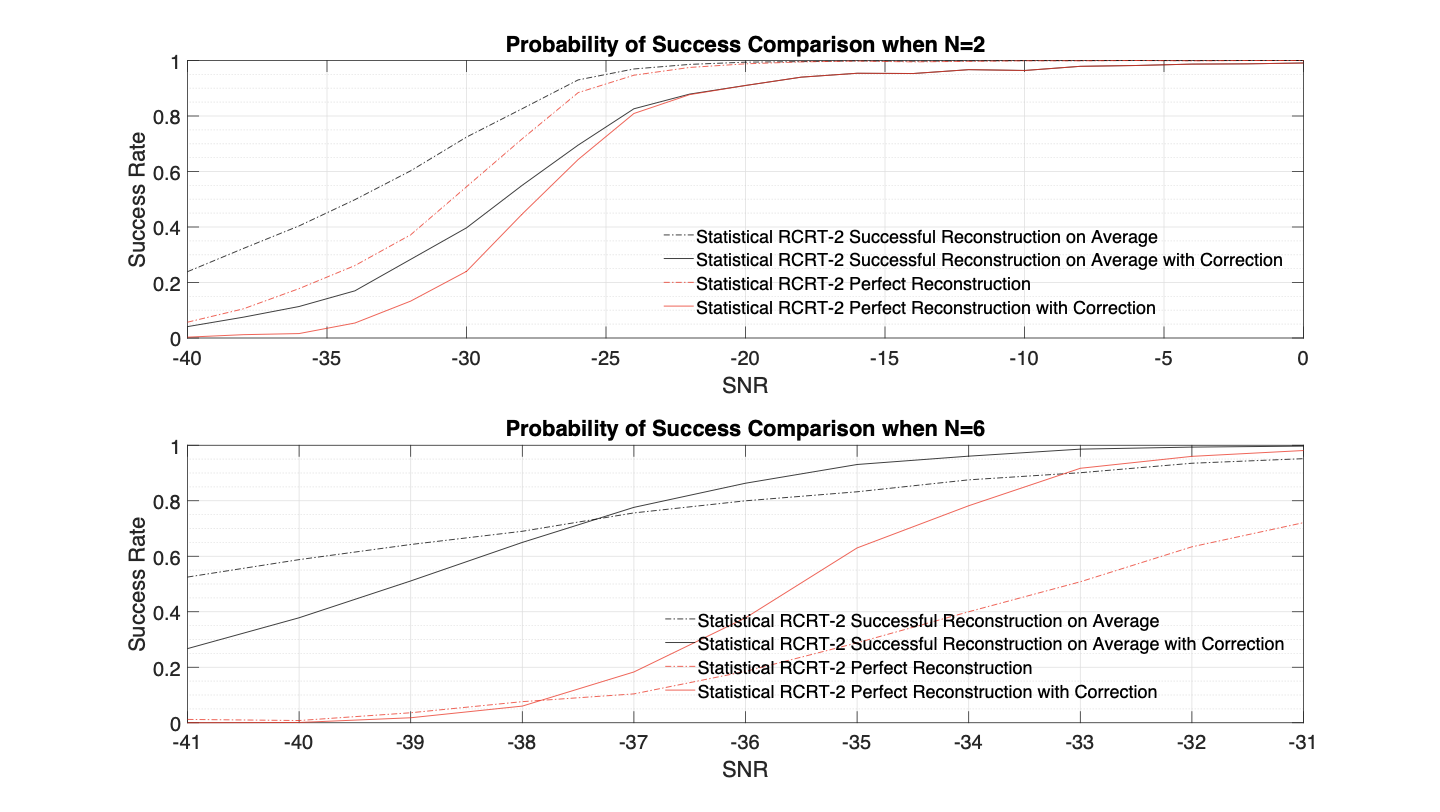
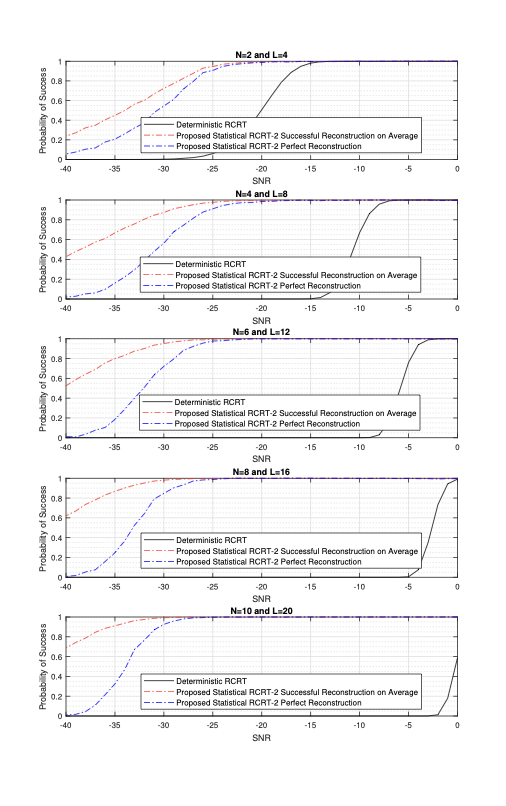
주요 성과: 실험 결과, 제시된 통계적 접근법이 기존의 결정론적 방식보다 높은 노이즈 상황에서도 훨씬 더 강건한 성능을 보였다. 특히 잔차 오류 정정 코드를 도입함으로써 강건성을 더욱 향상시켰다.
의미 및 활용: 이 연구는 CRT 기반 복원 과정에서의 통계적 접근법을 첫 번째로 제시한 것으로, 특히 고노이즈 환경에서 안정적인 성능을 보장하는 데 큰 의미가 있다. 이러한 방법은 신호 처리, 암호학 등 다양한 분야에서 활용될 수 있으며, 복잡한 시스템의 모니터링 및 예측에도 도움이 될 것으로 기대된다.
📄 논문 발췌 (ArXiv Source)
📊 논문 시각자료 (Figures)