토마스 샘플링을 이용한 공급측 플랫폼의 헤더 비딩 전략 최적화
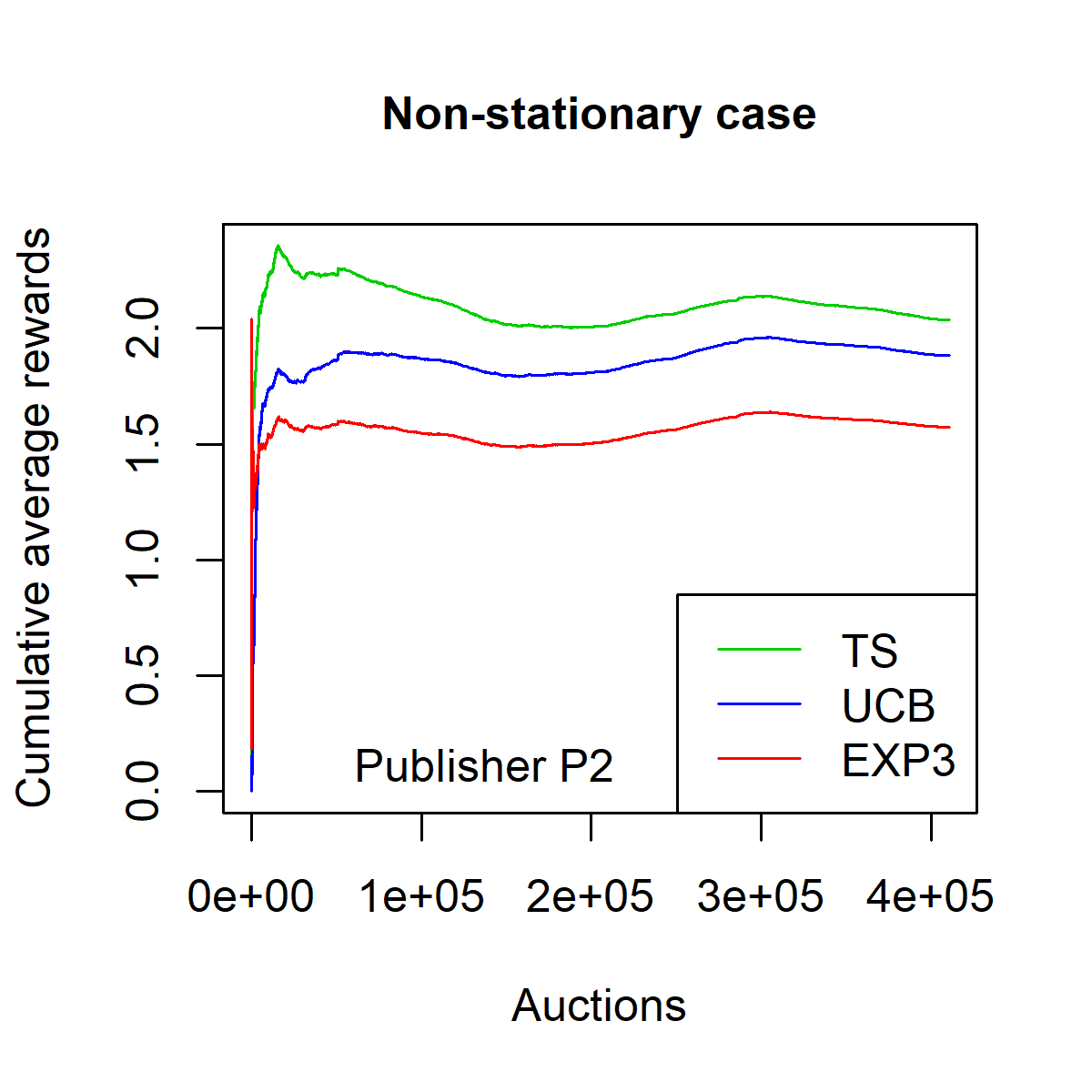
지난 10년 동안 디지털 미디어(웹 또는 앱 출판자)는 실시간 광고 경매를 사용하여 광고 공간을 판매하는 것을 일반화했습니다. 여러 경매 플랫폼인 공급 측면 플랫폼(SSP)이 생성되었습니다. 이러한 다수성으로 인해 출판자는 SSP들 간의 경쟁을 만들기 시작했습니다. 이 설정에서는 두 가지 연속적인 경매가 진행됩니다 각 SSP에서 제2 가격 경매와 SSP들 사이에서 이루어지는 제1 가격 경매인 헤더 입찰 경매입니다. 본 논문에서는 다른 SSP들과 경쟁하는 하나의 SSP를 고려합니다. 이 SSP는 광고주가 광고 공간을 구매하고자 할 때 중개자의 역할을 하며, 출판자가 광고 공간을 판매하길 원할 때도 마찬가지입니다. 그리고 광고주의 요구에 맞게 최대한 많은 광고를 전달하면서 최소한의 비용으로 경매에 참여하기 위한 입찰 전략을 정의해야 합니다. 이 SSP의 수익 최적화는 컨텍스트 밴딧 문제로 표현될 수 있으며, 컨텍스트에는 광고 기회에 대한 정보가 포함됩니다. 예를 들어 인터넷 사용자 또는 광고 배치 속성과 같은 정보입니다. 클래식한 다중 팔레트 밴딧 전략(UCB와 EXP3의 원본 버전을 포함)은 이 설정에서 효과적이지 않으며, 수렴 속도가 낮습니다. 본 논문에서는 이러한 상관관계를 쉽게 고려할 수 있는 Thompson Sampling 알고리즘의 변형을 설계하고 실험합니다. 이 베이지안 알고리즘과 입자 필터를 결합하여 비정상성을 다룰 수 있습니다. 이를 통해 경매에서 승리하기 위해 극대화해야 하는 최고 입찰 가격의 분포를 순차적으로 추정할 수 있습니다. 우리는 이 방법론을 두 개의 실제 경매 데이터셋에 적용하고, 더 전통적인 접근법보다 크게 우수함을 보여줍니다. 본 논문에서 정의된 전략은 전 세계 수천 명의 출판자에게 배포될 계획입니다.