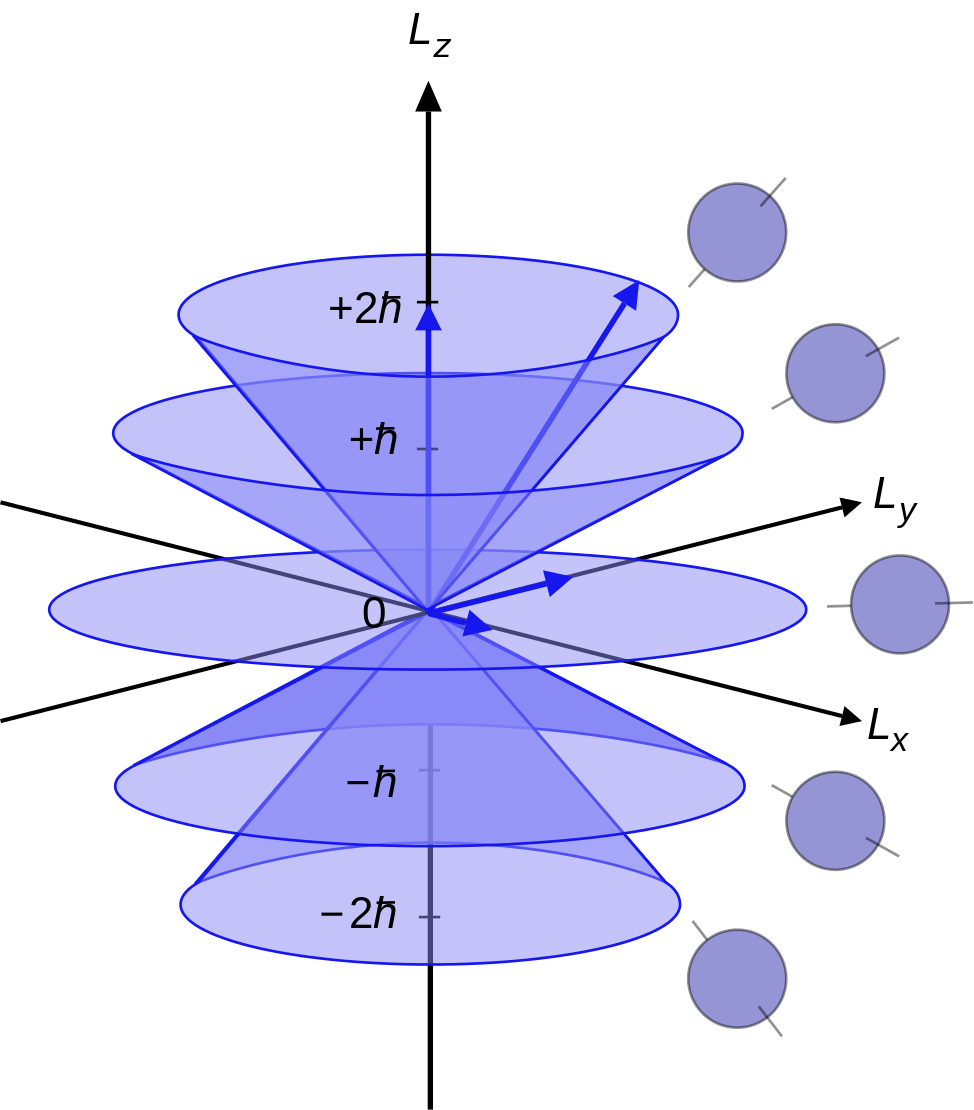
확률을 중심에 두다 힐베르트 공간이 생성하고 제약하는 확률
본 연구에서는 Bub(2016)의 상관 배열과 Pitowsky(1989b)의 상관 다면체를 사용하여 Mermin(1981)이 제안한 쌍방 탄성 상태에서의 스핀-$ frac{1}{2}$ 입자 측정 실험 설정을 분석합니다. 양자역학에 의해 허용되는 상관 관계의 클래스는 비신호 다면체 내부에 있는 타원 체로 표현됩니다. 국소 은닉 변수 이론으로 가능한 상관 관계의 클래스는 이 타원 체 내부에 들어가는 사면체로 나타납니다. 본 연구에서는 이를 스핀이 임의인 입자 쌍으로 확장하였습니다. 양자역학에 의해 허용되는 상관 관계의 클래스는 여전히 타원 체로 표현되며, 국소 은닉 변수 이론에 의해 허용되는 하위 클래스는 점점 더 많은 꼭지점과 면을 가지게 되어 타원 체에 가까워집니다. 이러한 결과를 통해 Bub의 해석처럼 양자역학의 해석을 주장합니다. 확률 및 기대값은 이 해석에서 기본적입니다. 그들은 힐베르트 공간 내 벡터들 간의 내적에 의해 결정됩니다. 이러한 벡터는 양자 세계에서 실제로 무엇이 있는지 표현하는 것이 아닙니다. 서로 다른 측정 집합의 값을 위한 확률 분포 패밀리를 인코딩합니다. 클래식 이론처럼, 이러한 값들이 결국에는 양자 세계에서 실제적인 것을 나타냅니다. 힐베르트 공간은 가능한 그러한 값들의 조합에 제약을 가하고 있습니다. 이런 제약들은 Minkowski 시공간이 사건의 가능 시공간적 배치에 대한 제약을 가하는 것과 유사합니다. 본 논문에서 도출된 타원 체 방정식은 통계 및 확률 이론의 더 오래된 문헌에서도 찾을 수 있는 일반적인 상관 계수 제약입니다. Yule(1896)이 이미 이러한 제약을 언급했으며, De Finetti(1937)는 이를 기하학적으로 해석했습니다.