레언캣 벤치마크로 본 카테고리 이론의 정식화
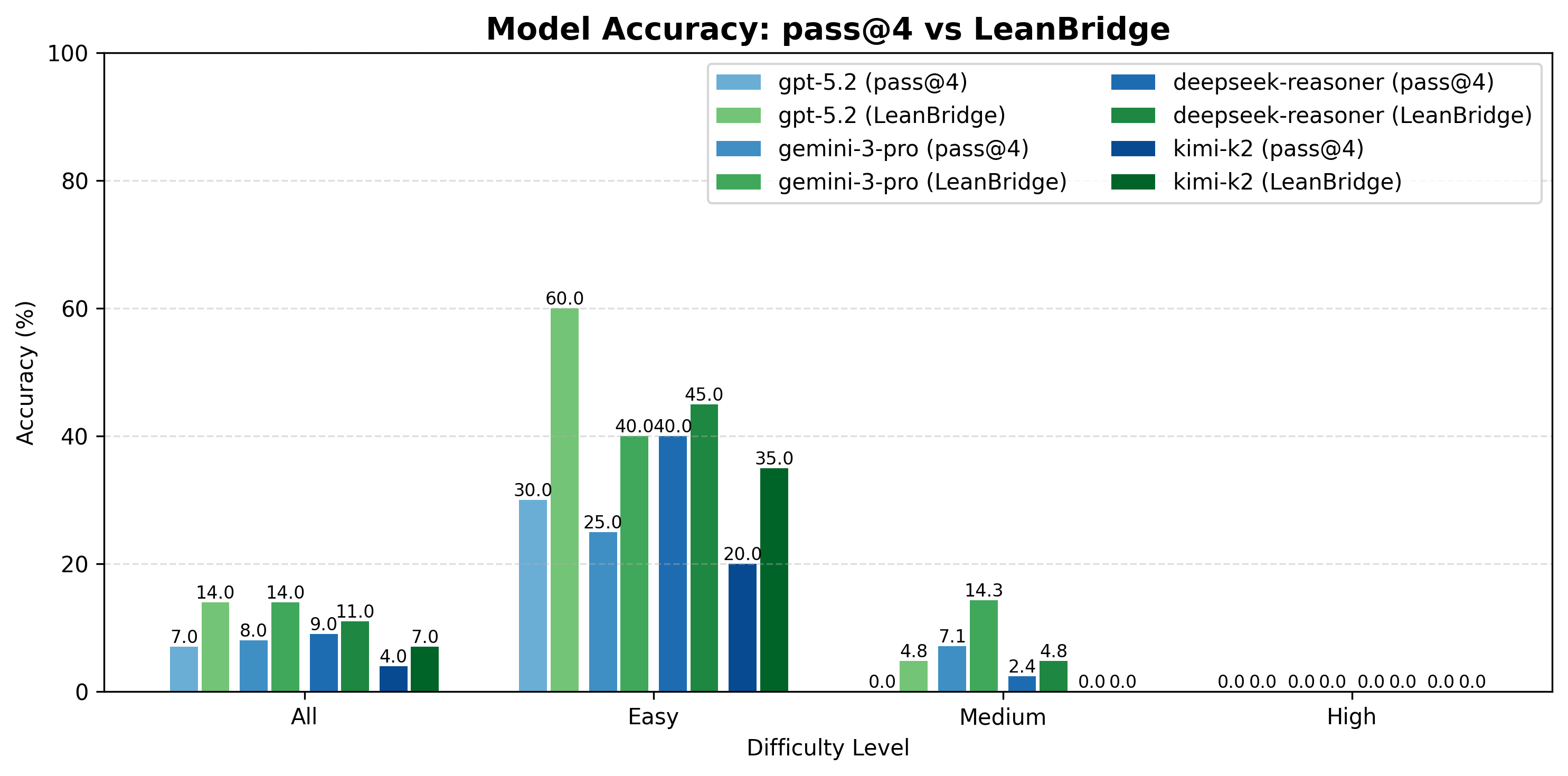
이 논문에서는 대규모 언어 모델(LLM)과 에이전트 훈련을 활용한 형식적 정리 증명의 최근 발전을 다룹니다. 특히, 카테고리 이론 문제를 포함한 벤치마크 **LeanCat**을 제안하며, 현존하는 자동 증명기에 대한 평가 결과를 제공합니다. LeanCat은 카테고리 이론의 다양한 주제에 걸쳐 100개의 정리를 포함하며, 각 문제는 난이도 분류를 통해 Easy, Medium, High로 구분됩니다.
'Logic in Computer Science' 카테고리의 모든 글

이 논문에서는 대규모 언어 모델(LLM)과 에이전트 훈련을 활용한 형식적 정리 증명의 최근 발전을 다룹니다. 특히, 카테고리 이론 문제를 포함한 벤치마크 **LeanCat**을 제안하며, 현존하는 자동 증명기에 대한 평가 결과를 제공합니다. LeanCat은 카테고리 이론의 다양한 주제에 걸쳐 100개의 정리를 포함하며, 각 문제는 난이도 분류를 통해 Easy, Medium, High로 구분됩니다.
우리는 퍼지 형식적 문맥에서 가능주의 추론을 위한 이중 정렬 가중 모달 논리를 소개한다. 이 논리의 구문은 고전적인 필수성($ Box$)과 충분성($ boxminus$) 모달 연산자를 포함하는 두 가지 유형의 가중 모달 연산자를 포함하며, 그 공식들은 가능성 이론을 기반으로 한 퍼지 형식적 문맥에서 해석된다. 논리는 모든 퍼지 컨텍스트 모델에 대해 emph{정합적}인 축소화를 제시한다. 또한 논리의 필수성과 충분성 프래그먼트는 각각 모든 퍼지 컨텍스트 모델에 대해 개별적으로 완전하다. 논리의 표현력은 몇 가지 예시를 통해 강조된다. 형식적 문맥이 형식 개념 분석(FCA)의 기본 구조인 경우, 우리는 FCA의 세 가지 주요 개념, 즉 형식적 개념, 객체 중심 개념 및 속성 중심 개념을 각각 퍼지 형식적 문맥에서 그에 해당하는 $c$-컷 개념으로 일반화한다. 그런 다음 우리의 논리 언어가 이들 모든 일반화된 개념을 표현할 수 있음을 보인다. 마지막으로, 우리는 논리를 다중 관계 퍼지 컨텍스트에 대한 추론 확장 가능성의 가능성을 보여주며, 여기서 서로 다른 퍼지 관계의 불리안 조합이 허용된다.
검색어를 입력하세요