추가 제조 후 처리를 위한 자동 지지구조물 제거 방법
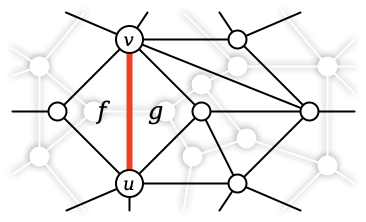
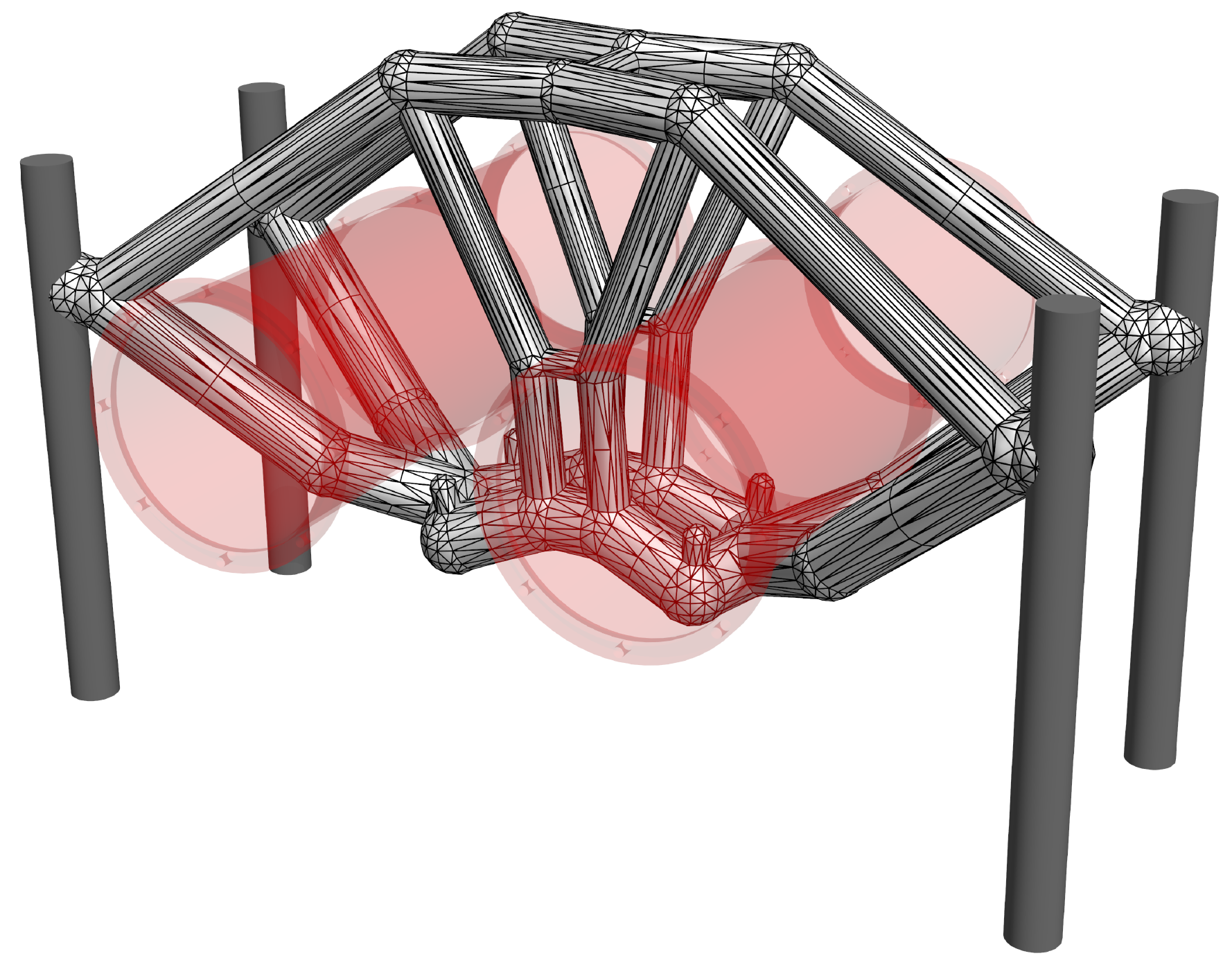
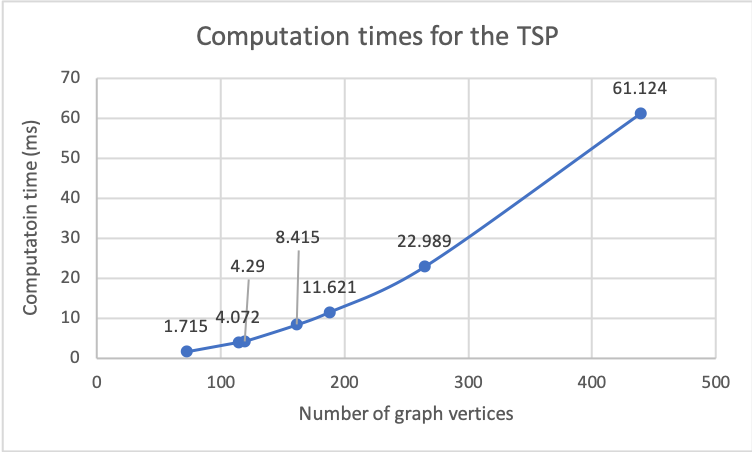
3D 프린팅(가장 가까운 형태 제조) 과정은 종종 실제 제작하려는 디자인에 가까운 형태를 만들어냅니다. 이 과정에서 추가적인 지지 구조물(또는 스크래프olding이라고도 함)이 포함되며, 이를 후처리 단계에서 제거해야 합니다. 본 논문에서는 다축 가공 도구를 사용하여 지지 구조물을 자동으로 제거하는 프로세스 계획을 생성하는 접근법을 설명합니다. 목표는 각 지지 구성 요소와 부품 사이의 접촉 영역을 분리하고, 진화 중인 가장 가까운 형태(남아 있는 지지 구성 요소를 포함)와 충돌하지 않으면서 가장 비용 효율적인 순서로 이를 수행하는 것입니다. 재귀 알고리즘은 각각의 지지 구성 요소가 부품에 연결되는 영역이 접근 가능한지 확인하고, 그들이 제거될 수 있는 방향을 결정합니다. 이러한 지역 중 하나마다, 접근 가능한 방향은 진화 중인 가장 가까운 형태와 도구 조립체 사이의 충돌 없는 공간에서 섬유 로 나타납니다. 접근 가능한 지지를 제거하기 위한 순서를 정하기 위해 알고리즘은 엣지가 섬유 간 리만 거리로 가중치가 부여된 탐색 그래프를 생성합니다. 가장 저렴한 프로세스 계획을 얻기 위해 탐색 그래프에서 트래블링 세일즈맨 문제(TSP)를 해결합니다. TSP의 솔루션으로부터 얻은 구성 시퀀스는 충돌 없는 경로를 찾기 위한 입력으로 사용됩니다. 지지 구조물을 제거한 부품은 전통적인 가공을 통해 예정된 디자인을 완성할 수 있습니다. 방법의 효과는 3D 벤치마크 예제를 통해 입증되었습니다.